计及分时电价的光伏发电置信容量评估

许文超，范文飞，高　君，任佳依，顾　伟

（1.江苏省电力设计院，江苏南京211102；2.西南电力设计院，四川成都610065；3.东南大学电气工程学院，江苏南京210096）

计及分时电价的光伏发电置信容量评估

许文超1，范文飞2，高君3，任佳依3，顾伟3

（1.江苏省电力设计院，江苏南京211102；2.西南电力设计院，四川成都610065；3.东南大学电气工程学院，江苏南京210096）

光伏电源出力具有随机性、波动性和间歇性，对电力系统具有一定负面影响。通过采用峰谷分时电价措施引导用户来改变用电方式，对负荷曲线产生修正作用，使负荷与光伏出力变化趋势接近，提升两者之间的相关性，从而提升光伏电站的置信容量。在含有光伏发电的IEEE-RTS79系统中引入分时电，进行随机生产模拟，在计入光伏与负荷随机波动的情况下，对采用分时电价措施前后的系统可靠性进行评估；采用序贯蒙特卡洛法计算可靠性指标，采用弦截法得出接入光伏的置信容量，验证了分时电价措施提升光伏出力置信容量的效果。

光伏消纳；等效负荷曲线；分时电价；序贯蒙特卡洛算法

作为一种常见的可再生能源，太阳能逐步发展成为化石能源的主要替代能源，其应用越来越广泛。随着技术水平的不断提升，光伏发电成本呈现快速下降趋势，将占据越来越重要的地位。但光伏电源出力具有随机性、波动性和间歇性，对系统具有负面影响。需求侧资源的参与提高了电力系统灵活调节能力，对提高电力系统光伏消纳能力具有重要意义。

关于需求侧资源对于消纳间歇性能源的积极作用，国内外研究人员已经取得一定程度的研究成果。文献［1］建立了机会约束模型，采用需求响应措施提升风电消纳能力，但其需求响应措施未考虑响应时间，结果趋于乐观。文献［2］利用直接负荷控制（DLC）措施采用以制冷空调为例的居民热力学可控负荷（TCL）作为负荷响应资源，对风电波动进行抑制，一定程度上牺牲了用户的满意度，同时能消纳的风电波动幅度与TCL占负荷的比例密切相关。文献［3］通过可中断负荷措施和分时电价措施抑制风电波动，但风电本身的预测曲线是给定的，未展示不同预测场景下的应对措施。文献［4］采用实时电价措施消纳风电波动，从随机机组组合和确定机组组合两方面考察实时电价对于风电消纳的积极作用。在文献［5］中，研究人员尝试了调整光伏阵列的方向，使光伏发电出力峰值时段尽量与负荷峰值时段重叠，改善了光伏发电出力与负荷之间的相关程度，证实了该项措施有效提高了光伏发电置信容量。文献［6］采用Spearman秩相关系数评价光伏出力与负荷之间的相关性，并且通过平移每日光伏出力数据以改变光伏出力峰值时段的分布，使其接近日负荷峰值的时段的方法来提升光伏出力与负荷之间的相关性，得到了相关性越高，接入光伏置信容量越高的结论。

为了提升光伏出力与负荷之间的相关性，除了通过调节光伏电源侧的方法，还可以将负荷看作一种能够调度的资源，通过需求响应措施改变负荷的分布，达到提升相关性的目的。文中从负荷侧的角度，利用光伏和负荷的预测信息形成等效负荷曲线，采用峰谷分时电价措施，使得等效负荷曲线平缓化，提升光伏出力与负荷之间的相关性，进而提升接入光伏的置信容量和容量置信度，并且在IEEE-RTS 79系统中对方法效果进行验证。

1　峰谷分时电价优化模型

1.1等效负荷曲线

等效负荷曲线［7，8］是将光伏出力等效为负的负荷，再与负荷曲线合成而得。光伏接入电网后，等效负荷曲线的峰谷特征受光伏出力和负荷共同影响。示例如图1所示，图中CP代表容量渗透率［9，10］。

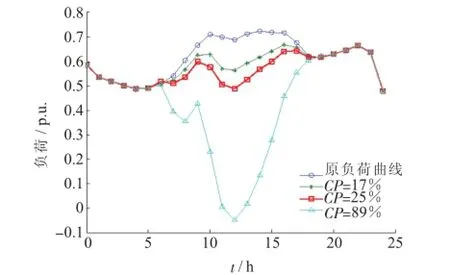
图1　不同容量渗透率下的等效负荷曲线

由图1可知，随着光伏容量的变化，等效负荷曲线峰谷状况也产生了相应的变化。当光伏容量渗透率较高时，通过分时电价措施缩小等效负荷曲线的峰谷差，可以使光伏出力和负荷的变化趋势接近，相关性提升。

1.2用户响应模型

合理的用户响应模型是峰谷电价制定的前提，也是预测电价实施后负荷转移情况的重要依据。各时段价格改变后，负荷在各时段之间发生转移。设各时段之间负荷转移量与各时段之间的相对电价差成正比，比例系数称为负荷转移率，则按峰、谷、平3类时段划分时，存在λpv，λpf，λfv3种负荷转移率，分别代表峰时段向谷时段、峰时段向平时段、平时段向谷时段的负荷转移率。消费者心理学模型的引入［11］使得负荷转移率可由分段函数表示。用户对于电价的响应，在电价未超过下限阈值Δpmin时，将会趋近于0。超过上限阈值Δpmax之后，电价增加也不会引起进一步的响应，此时转移率达到λmax。在这2个阈值之间，用户转移率和电价成正相关。负荷转移率和相对电价差的函数可表示为：

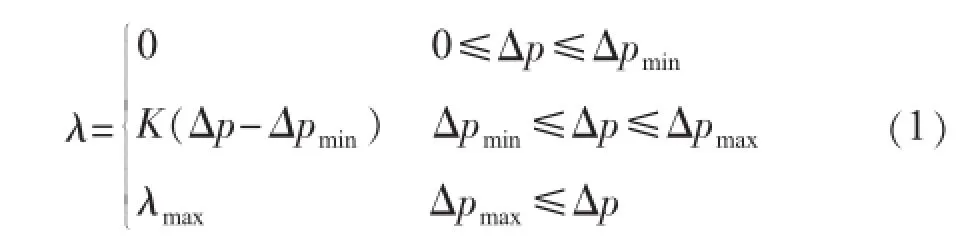
假设转移到某一时段的负荷按时间平均分配，考虑到时段长度不均等的情况，需要乘以代表时段长度比值的系数：

式中：Lp0，t，Lv0，t，Lf0，t分别为实施分时电价措施之前峰、谷、平的时段t的负荷；Lp1，t，Lv1，t，Lf1，t分别为实施分时电价措施之后峰、谷、平的时段t的负荷；λpv，λpf，λfv分别为峰谷、峰平、平谷时段之间的负荷转移率；np，nf，nv分别为峰平谷时段的长度；L¯p0，L¯f0，L¯v0分别为实施分时电价措施之前峰、谷、平各时段的负荷平均值。

1.3电价制定

针对需求响应的分时电价制定可以看作一个优化问题。为了使光伏出力与负荷变化趋势接近，采取将等效负荷曲线的峰谷差最小化的方法，目标函数为：

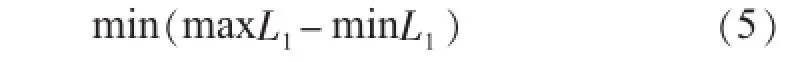
L1为实施分时电价之后的等效负荷曲线，是峰、谷、平电价pp，pv，pf的函数，规定优化后平时段电价与采用分时电价前平均电价p¯o相等，故实际优化决策变量只有pp和pv。对于供电方，实行分时电价前，供电方的销售收入E0为：

式中：q为实行分时电价前用户消耗的总电量。实行分时电价后供电方的销售收入E1为：

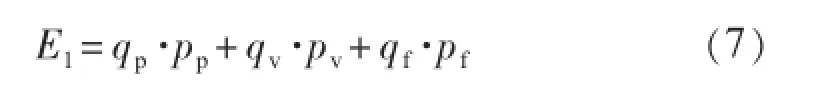
式中：qp，qv，qf分别为实行分时电价后峰、谷、平时段的用电量。

式中：Tp，Tv，Tf分别为峰、谷、平时段的集合。实施分时电价后，供电公司可以节约一部分由于减少机组频繁启停、延缓电网建设带来的成本［4］，因此可通过降低电价收入的形式体现出来，以让利系数r表示。

对于用户要求实施分时电价之后总电费不多于实施分时电价前总电费：

设定高峰电价可为低谷电价的4倍，则：

对以上优化模型进行求解，可以得到合适的各时段电价。进而通过式（2—4）得到实施分时电价之后的等效负荷曲线。

2　光伏出力与负荷模型

2.1光伏出力模型

为了保证用户有充分的准备时间调节用电计划，分时电价的制定在日前进行，因此需要以日前的负荷与光伏预测信息作为依据，进行分时电价的制定。但是实际曲线会与预测情况有一定偏差，在评价置信容量时需要将随机波动性考虑在内。

文中将光伏实际输出功率表示为预测出力与预测偏差量的合成形式：

式中：PPV为光伏实际出力；PPV，f为光伏预测值；ΔPPV为预测偏差。根据文献［12］，预测偏差可视为服从均值为0，方差为σ2PV，i的正态分布：

式中：σ2PV，i表示时段i的预测误差的标准差。

依据文献［13］拟合函数关系查得次日24 h光照强度预测误差分布标准差，以文献［12］中的光伏系统为例，得出以标幺值形式表示的光伏预测偏差的标准差，如表1所示。

2.2负荷模型

表1　各时段的光伏出力预测标准差

为体现负荷与光伏出力之间的相关性，负荷也需要采用保留时序信息的时间序列模型。时间序列负荷模型采用小时最大尖峰负荷与年最大负荷的比值来表示仿真时刻的负荷期望值，按年表次序形成负荷模型，表达式如下：

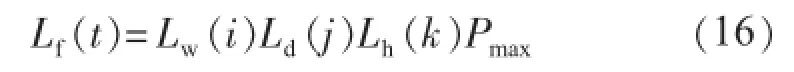
式中：Lf（t）为预测负荷值；Pmax为年峰荷；Lw（i）为一年中的第i周负荷峰值占年负荷峰值的百分比；Ld（j）为第i周的第j日负荷峰值占周负荷峰值的百分比；Lh（k）为每日的第k小时负荷峰值占日负荷峰值的百分比，即每日的典型负荷曲线。各季节工作日典型负荷曲线如图2所示。Lw（i），Ld（j），Lh（k）在文中采用的仿真系统IEEE-RTS79系统中已经给出，可以据此形成一年8760 h的负荷曲线。

图2　各季节工作日典型负荷曲线

负荷预测值与实际值之间的偏差也具有波动性，这种波动性也可采用正态分布来描述，即t时刻的负荷L（t）为：

3　光伏发电置信容量评估

3.1光伏发电置信容量评估指标

采用有效载负荷容量（ELCC）来衡量光伏发电的可信容量。ELCC表征在保持间歇式发电接入系统前后可靠性不变的情况下，系统负荷可以增加的容量。接入光伏电源可以提高电力系统的可靠性，此时系统允许接入额外的负荷，可以将可靠性水平维持在接入电源前的水平。

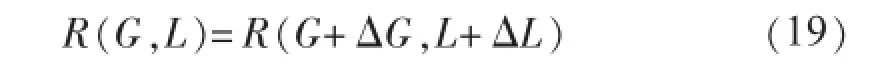
式中：R为可靠性指标，是与总装机容量和负荷有关的函数，常见的可靠性指标有失负荷期望（LOLE）、电量不足期望（EENS）等；G为系统初始装机容量；ΔG为新增电源额定容量；L为系统原有负荷；ΔL为由新增电源所能承担的额外负荷。使式（19）成立的ΔL即为新加入电源的置信容量。对于一个给定的系统，可以求取系统在接入一定量光伏电源和额外负荷之后的可靠性指标，然后采用弦截法迭代求解置信容量。文中选择LOLE作为可靠性指标，并且通过序贯蒙特卡洛仿真法对LOLE进行求解。

3.2序贯蒙特卡洛法

评估光伏发电系统的常用方法有解析法和模拟法。解析法一般将光伏发电等效为多状态的常规机组，无法反映光伏发电的时序特性，可能引入一定的误差，所以推荐采用模拟法进行评估。模拟法主要包含非序贯蒙特卡洛法和序贯蒙特卡洛法。非序贯蒙特卡洛法缺乏对机组状态变化的时序性的反映，无法体现光伏出力与负荷的相关性对置信容量造成的影响，所以文中采用序贯蒙特卡洛法计算LOLE。常规机组具有正常运行和故障状态2种状态，设正常运行持续时间为t1，故障状态持续时间，即检修消耗时间为t2。一般t1和t2均服从指数分布：

式中：γ为服从［0，1］均匀分布的随机数；tMTTF和tMTTR分别为元件的平均工作时间和平均修复时间。以小时为单位对机组的状态进行抽样，形成全年8760 h的机组每小时可用容量序列。将全年小时负荷减去全年光伏小时出力，得到全年的等效负荷曲线，分别对实施分时电价前后的全年等效负荷曲线进行可靠性评估。

采用式（22）的方差系数来评价序贯蒙特卡洛仿真的精度：

式中：β为方差系数；V（I¯LOLE）为样本方差；ILOLE为可靠性指标。随着运行年数nyear的不断增加，β会将趋于下降，β值越小，序贯蒙特卡洛法的精度就越高，文中以β＜0.05作为序贯蒙特卡洛法的收敛判据。

3.3弦截法

采用弦截法进行迭代，逐步调节新增负荷量，计算不同新增负荷之下的LOLE指标，使可靠性指标LOLE保持在接入光伏之前的水准，从而得到实施分前后接入光伏的置信容量。系统原始峰荷为L0，原始系统可靠性指标为R0，此时系统状态对应图3中点P0（L0，R0）。加入容量为Gpv的光伏电站，同时峰荷不变L1=L0，系统的可靠性指标R1；峰荷L2=L0+Gpv时增加等容量光伏可靠性指标R2，得到点P1（L1，R1）和P2（L2，R2）。此时P1位于所求点P的左侧，P2位于所求点P的右侧。过点P1和P2作直线交直线R=R0于P'3（L3，R0），以L3作为新的负荷进行计算，得到可靠性指标R3，形成点P3（L3，R3），P3比P1靠近所求点P。过点P3和P2作直线交直线R=R0于P'4（L4，R0），以L4作为新的负荷进行计算，得到可靠性指标R4。重复以上步骤，交点将逐步逼近所求点P。过程如图3所示。

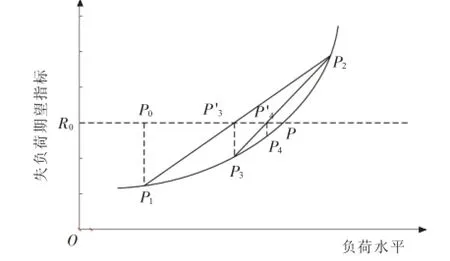
图3　弦截法示意图

4　算例分析

以IEEE-RTS79系统为例，采用Matlab编程进行算例仿真，该系统包括32台发电机，总装机容量为3405MW，系统最大负荷为2850MW。接入570MW光伏电站（占峰荷的20%）。负荷波动标准差σLoad=3% μLoad。以典型光伏出力场景与典型负荷形成等效负荷曲线，优化后得到各时段负荷修正量，将其加入年负荷曲线后，采用弦截法得到实施分时电价前后，加入光伏发电的置信容量。以春季周末负荷曲线以及晴天光伏出力为例，合成等效负荷曲线，如图4所示。

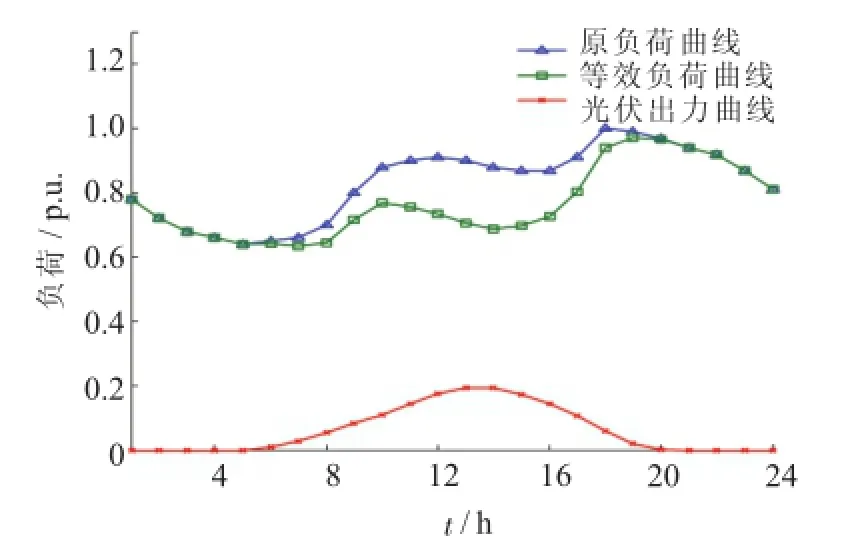
图4　等效负荷曲线

以式（5—13）的优化模型对等效负荷曲线进行电价优化，由得到的电价方案带入式（2—4）进而得到调整后的等效负荷曲线，实施分时电价前后的等效负荷曲线对比如图5所示。

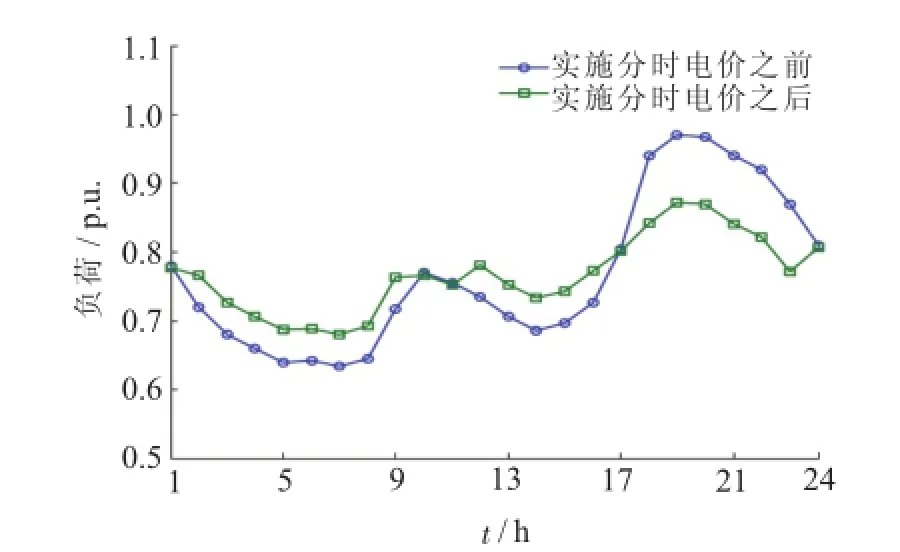
图5　分时电价实施前后等效负荷曲线对比

图6为实施分时电价前后负荷与光伏曲线对比，从图中可以看出，负荷曲线发生了明显改变。实施分时电价前，负荷与光伏出力的秩相关系数为0.06，实施分时电价后，秩相关系数为0.84，负荷与光伏出力的相关性得到了明显提升。

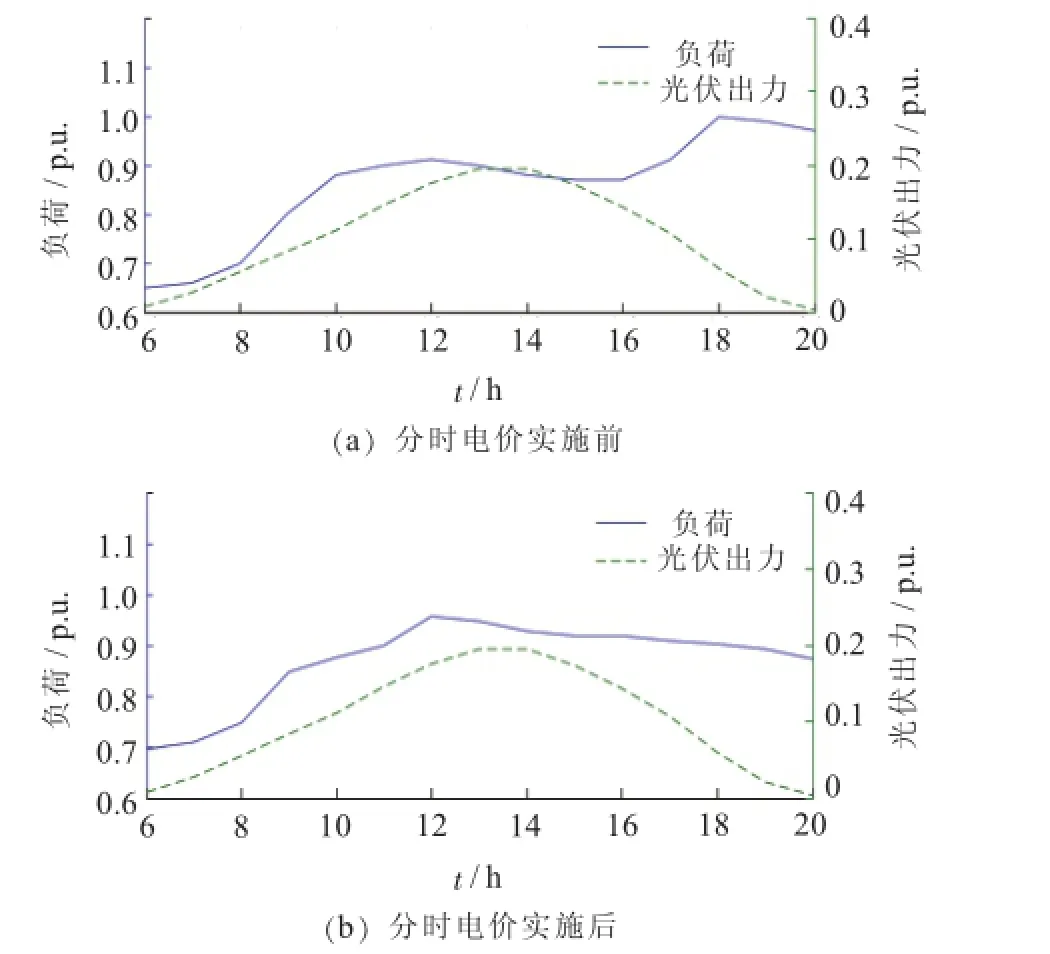
图6　实施分时电价前后负荷与光伏曲线对比

以式（5—13）优化模型对等效负荷曲线进行电价优化，得到各种情况光伏出力之下典型时段划分以及电量变化量，只考虑日内的负荷转移，忽略不同日以及不同季节之间的负荷转移，对年等效负荷曲线进行修正，得到图7年负荷曲线。由图7可见日内峰谷差有所减少，等效负荷曲线平缓化，同时总负荷量保持不变。

图7　采用分时电价措施后年负荷曲线

采用序贯蒙特卡洛法进行生产模拟。通过弦截法不断迭代调整负荷，分别针对无TOU措施、TOU措施下用户响应积极性一般、用户响应积极性较高3种情况计算接入光伏置信容量（响应积极性较高时，用户转移负荷量上限更高）结果如表2所示。

表2　不同情况下的光伏置信容量

可知用户响应积极性越高，接入光伏置信容量和容量置信度越高。

5　结束语

为了提高光伏出力与负荷的相关性，采用峰谷分时电价手段对等效负荷曲线进行优化，使得等效负荷曲线平缓化，光伏曲线与负荷的相关性得到改善，提升了光伏发电置信容量。文中建立了基于不同预测场景的光伏出力模型与时序负荷模型。将以上模型应用于IEEE-RTS 79系统中，采用序贯蒙特卡洛法进行仿真求取不同情况下的可靠性指标LOEE，通过弦截法得出光伏的置信容量，证明了分时电价措施提升系统接入光伏发电的置信容量的积极作用。

［1］艾欣，刘晓.基于需求响应的风电消纳机会约束模型研究［J］.华北电力大学学报（自然科学版），2011，38（3）：17-22.

［2］艾欣，赵阅群，周树鹏.适应清洁能源消纳的配电网直接负荷控制模型与仿真［J］.中国电机工程学报，2014，34（25）：4234-4243.

［3］王蓓蓓，刘小聪，李扬.面向大容量风电接入考虑用户侧互动的系统日前调度和运行模拟研究［J］.中国电机工程学报，2013，33（22）：35-44.

［4］刘小聪，王蓓蓓，李扬，等.基于实时电价的大规模风电消纳机组组合和经济调度模型［J］.电网技术，2014（11）：2955-2963.

［5］WATTM.E，OLIPHANT M，OUTHRED H，et al.Using PV to MeetPeak Summer Electricity Loads［C］//Proceedingsof the 41st Conference of the Australian and New Zealand Solar Energy Society，Melbourne，Australia：2003：26-29.

［6］梁双，胡学浩，张冬霞，等.基于随机模型的光伏置信容量评估方法［J］.电力系统自动化，2012，36（13）：32-37.

［7］李卫良，黄堃，陈璐，等.采用可控负荷平滑光伏发电功率波动的需求响应策略［J］.江苏电机工程，2014，33（2）：40-43.

［8］薛斌.基于GAMS的光伏发电消纳体系研究［J］.江苏电机工程，2014，33（2）：4-7.

［9］易桂平，胡仁杰.太阳能光伏电池建模与动态特性仿真［J］.江苏电机工程，2014，33（5）：32-35.

［10］江林.分布式光伏发电并网的国内外政策分析与启示［J］.江苏电机工程，2013，32（3）：66-68.

［11］王秀丽，武泽辰，曲翀.光伏发电系统可靠性分析及其置信容量计算［J］.中国电机工程学报，2014，34（1）：15-21.

［12］施琳，罗毅，涂光瑜，等.微网功率不确定性模型及其在旋转备用优化中的应用［J］.电力系统保护与控制，2013，41（18）：37-44.

［13］LORENZ E，HURKA J，HEINEMANN D，etal.Irradiance Forecasting for the Power Prediction of Grid-connected Photovoltaic System s［J］.IEEE Journal of Selected Topics in Applied Earth Observationsand Remote Sensing，2009，2（1）：2-10.

Photovoltaic Generation Capacity Credit Evaluation Taking Account of TOU M ethod

XUWenchao1，FANWenfei2，GAO Jun3，REN Jiayi3，GUWei3
（1.Jiangsu Electric Power Design Institute，Nanjing 211102，China；2.Southwest Electric Pow er Design Institute，Chengdu 610065，China；3.Schoolof Electrical Engineering，SoutheastUniversity，Nanjing 210096，China）

The photovoltaic output power is obvious random，fluctuant and interm ittent，w hich has certain extent of negative effectson power system.TOUmethod isadopted to guide the consumers to change the power consumptionway.And the load profile is regulated to track PV pow er output and im prove the correlation of them，w hich leads to increment of PV capacity credit.TOU method is introduced in the IEEE-RTS79 system with photovoltaic generation to simulate the probabilistic production.And the reliability of the system before and after using TOU method is evaluated w ith taking into account of stochastic fluctuation of load and PV output.Then the reliability indicator is calculated with sequentialMonte Carlo algorithm，and PV capacity credit is obtained w ith secantmethod.The resultverifies the effectiveness of TOU method on improving PV capacity credit.

pphotovoltaic pow er accommodation；equivalent load profile；TOU；sequentialmonte carlo algorithm

TM 76

A

1009-0665（2016）05-0035-05

许文超（1979），女，江苏南京人，高级工程师，从事电力系统规划、新能源并网、分布式电源微电网等方面的研究；

范文飞（1990），男，四川成都人，硕士研究生，研究方向为需求侧管理；

高君（1991），男，山东青岛人，硕士研究生，研究方向为配电网的优化运行和负荷管理；

任佳依（1992），女，浙江台州人，硕士研究生，研究方向为配电网运行优化；

顾伟（1981），男，江苏南京人，博士生导师，主要从事智能电网、可再生能源接入技术及电能质量分析控制等方面的研究。

2016-04-12；

2016-07-01

∶国家自然科学基金项目（51477029）