数学课堂如何引导学生进行深层思维
2016-10-19李丽君
李丽君
(河北省唐山市路南实验小学)
数学课堂如何引导学生进行深层思维
李丽君
(河北省唐山市路南实验小学)
目前,在数学教学中有一个很普遍的现象,那就是不少学生基础知识掌握得很好,做基础练习时得心应手,可是一遇到稍难一点的练习题时,却无从下手。究其原因,是学生的思维深度停留在表层,对题目进行深层思维的能力不够。那么,在习题教学中应该如何引导学生进行深层思维呢?这是数学老师应该思考的问题。
数学教学;解决问题;数学思维;深层思维
数学需要自我的理解与推理,通过推理获得数学发展的深层思维,从而达到融会贯通的目的,在学生理解基础知识的前提之下,引导他们进行深层的感悟与思考,达到以不变应万变的效果。笔者试结合具体的课例论及如何在教学中培养学生的深层思维能力。
一、一题多解,发展深层思维
一题多解重在让学生自己思维,让学生自觉地动脑、动手,老师只是引导,充分发挥学生自己的聪明才智,而不是多种方法全由老师讲解,让学生整理。一题多解的有效性学习思路是学生想、讨论,老师最后将方法汇总。
例如:全班42人去公园划船,租10只船正好坐满。每只大船坐5人,每只小船坐3人。租的大船和小船各有多少只?
学生首先想到的有序列列举法。
9×5+3=48,8×5+3×2=46,7×5+3×3=44,6×5+4×3=42,直至人数正好为止。
也有不少学生想到假设法,先假设大船和小船一样多,再根据总人数调整。
5×5+5×3=40,和42人比较,少了2人,那增加大船只数,6× 5+4×3=42正好。
在此基础上,我引导学生从极端情况入手进行假设,学生假设全是大船则有10×5=50(人),比42人多了50-42=8人,那就要减少大船的只数,每减少一只大船就少了5-3=2人,必须少了8÷2=4只大船,人数才正好。从而求出大船是10-4=6只,小船是4只。
在此之后,我鼓励学生用方程的方法来解。在学生给出多种解法之后,还要组织学生进行比较,从而找出这些方法之间的关联,分析这些方法的优劣所在。
在数学课堂上,适时地通过一题多解激发学生的智慧,正是数学一题多解的魅力所在。教师只需努力营造一个接纳的、支持性的、宽容的课堂氛围,创设能引导学生主动参与的教育环境,摆脱枯燥的说教,讲题之际善于倾听学生的理解,给学生思维的空间。
二、一题多变,发展深层思维
在解决这个问题时,不少学生是通过画图的方法来解决的,根据题意不难画出下面这样的图。在学生画图时,我细细观察,画的思路基本上是先画第一支蜡烛的高度,然后将其平均分成5份,将最后一份涂上颜色,然后画出第二支蜡烛的剩余部分,最后再补上燃去的部分。根据图,学生很容易得出这两支蜡烛原来长度的比是5∶3。
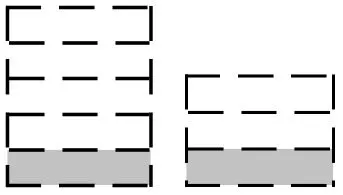
如果此题的练习仅仅到此结束,学生仅仅进行了浅层次的思维,这也枉费了编者设计此题的苦心,因为编者的意图不是让学生用画图的方法解决此题。因此,在教学时,我追问了学生一句:“如果这儿第一支不是燃去的,而是呢?”。学生根据刚才的解题经验,很容易画出下图,得出比是5∶6。
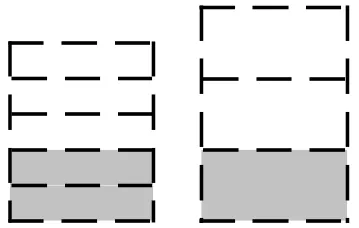
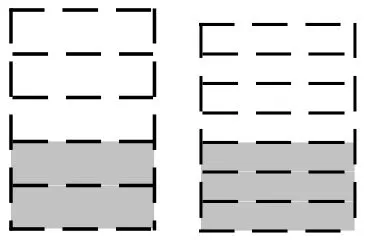
此时,我提醒大家:“这题就一定要用画图的方法才能解决吗?你能从题中找出数量关系吗?”
很快,学生就得出了等量关系:第一支剩下的长度=第二支剩下的长度。
根据这个关系式,学生可以将其变形为下面这样:
根据比例的基本性质,比例的内项之积等于外项之积,可以推出
至此,学生已得到这题结果,我让学生再回顾整个解题过程,并理解一下前面的两题不用画图的方法能不能像这样解决。
原题中蜡烛燃烧后剩下的部分都是一份,这具有特殊性,所以学生画图能立即看出结果,而后来的两次改编,逐步引导学生从特殊性向一般性探索,从而得出这类题的一般解法。在这个探索过程中,毫无疑问,学生的深层思维能力得到了锻炼。
可见,在小学数学教学中,培养学生深层思维能力的途径是多种多样的。科学地、经常地、多渠道地培养学生的深层思维,为他们的思维发展提供基点,让他们能在原有的基础上,思维能力得到不同程度的提升,从而提升数学学习的能力。
高峰官.优化数学教学策略,促进学生深度学习[J].科技文汇:下旬刊,2014(9).
·编辑杨国蓉
