考虑滞时电量的水电中期调度拉格朗日松弛方法

2016-10-18李保健武新宇申建建

水利水电科技进展 2016年4期

关键词：乘子梯级出力

李保健，武新宇，申建建

（1.大连理工大学水电与水信息研究所，辽宁大连 116024；2.华北水利水电大学水利学院，河南郑州 450045）

考虑滞时电量的水电中期调度拉格朗日松弛方法

李保健1，2，武新宇1，申建建1

（1.大连理工大学水电与水信息研究所，辽宁大连 116024；2.华北水利水电大学水利学院，河南郑州 450045）

针对梯级水电站群中期调度水流滞时问题，引入滞时电量概念，建立了梯级水电站群中期调度期末蓄能最大模型；采用基于两阶段次梯度法乘子更新策略的拉格朗日松弛方法进行模型求解，第一阶段通过系数递增策略快速确定乘子初始值，第二阶段采用递减策略加快算法收敛速度。以澜沧江中下游梯级6座水电站群中期优化调度为实例进行仿真，结果表明，所提出的求解方法能提供较好的求解质量；考虑滞时电量能提高水电系统的期末蓄能，中期调度需充分考虑调度结果的后效性。

梯级水电站群；优化调度；中期调度；蓄能最大模型；滞时电量；拉格朗日松弛方法

水电中期优化调度是指以日为时段，未来几天内的优化调度，是水电优化调度的主要环节之一。由于径流预报精度和预见期的限制，水电中期调度会受到来水不确定性的影响，但实践中通常将其作为确定性问题以充分利用气象和水文预报信息。在梯级最上游和最下游距离较远时，梯级水电站间的水流滞时问题不可忽略，这与短期调度有相似之处。由于调度时段以日为步长，上游水库某时段出库水量在相同或其后一个时段全部流入下游水库的假设不成立，因而存在某一时段上游出库水量在下游水库两个连续时段间分配的问题。

按照问题特点和求解方法的不同，水电优化调度模型［1］可以大致分为两类：第一类是给定各水库末水位，在调度期内按照调度目标调节水量时空分布，此类模型偏重于在满足各电站的中长期控制方式前提下，提高水能利用效率，是广义的以水定电方法，目标通常为发电量最大［2-5］、发电效益最大［6-7］等；第二类是给定各时段水电系统负荷需求，在各电站间分配出力［8］，是广义的以电定水方法，主要采用期末蓄能最大［9-10］和购电成本最小等模型，其中期末蓄能最大模型应用广泛，适用于梯级和跨流域水电站群负荷分配问题。水电站群优化调度算法众多［11-15］，但中期期末蓄能最大模型求解及应用上仍有很多问题需要解决。一方面由于受到负荷需求的强约束条件限制，求解较困难，常用的拉格朗日松弛算法［16-17］需乘子向量多次更新，计算效率受乘子向量更新策略和初始值影响较大，因而需结合实际问题研究具有较好实用性的乘子更新策略；另一方面，水流滞时和滞时电量影响也需充分考虑并进行合理简化。

本文建立了在径流确定性条件下考虑水流滞时的梯级水电站群中期调度期末蓄能最大模型，采用具有较高求解质量的拉格朗日松弛法，在建立对偶问题的基础上，以逐次逼近算法［18］求解对偶问题，以两阶段次梯度法进行乘子更新，并以澜沧江干流中下游已投产的6座梯级水电站群为实例，对模型进行了求解。

1 数学模型

给定梯级或者跨流域水电站群系统总出力过程进行负荷分配，是水电中期调度的一种重要方式，具有广泛的应用背景：在水电分级调度模式下，由于电力系统的约束和需求，上级水电调度部门常以未来几日总发电量过程对下一级水电调度部门下达计划，下一级水电调度部门在电站间进行出力分配，或者进一步以总发电量过程的方式将任务分解下达到所属再下一级的各水电调度部门；在前述第一类模型中，若在给定的水电控制方式下结果无法满足水电总出力上下限约束，则需要固定部分时段总出力为水电总出力上限或下限约束条件值进行负荷优化分配。这类问题一般采用调度期末蓄能最大或者调度期间耗能最小为分配准则，目的是在满足当前需求的前提下，尽量抬高发电水头，增加系统蓄能，为控制期后水电系统安全、稳定、经济运行创造条件。

在受到水流滞时影响时，应以滞时电量与期末蓄能之和最大作为目标函数。对上游出库流量在下游的时段间分配采用近似方法，即根据短期滞时确定不同出库流量级别在两个流达时段间的分配比例系数，据此建立中期期末蓄能最大模型。

1.1 目标函数

考虑滞时电量的期末蓄能最大模型目标函数为

其中

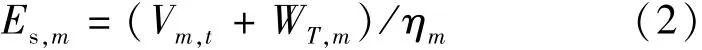
式中：Es，m为电站m及全部上游电站死水位以上水量在电站m可产生的电量；El，m为上游电站在电站m产生的滞时电量；Vm，t为电站m第t时段末死水位以上的蓄水量；ηm为电站m平均耗水率；WT，m为电站m的全部上游电站调度期末死水位以上蓄水量；WL，m为电站m全部上游电站滞时水量；M为跨流域水电站群参与计算电站的总数；T为计算时段总数；t为时段标号（t=1，2，…，T）。由于电站的滞时水量不仅受直接上游电站的影响，也受其他更上游电站的影响，尤其当电站m直接上游电站无调节能力或调节能力较差时，对滞时水量影响明显，需要考虑因此产生的滞时电量。

1.2 约束条件

a.水量平衡约束：

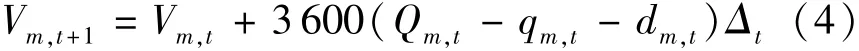
其中

式中：Qm，t为电站m第t时段的入库流量；qm，t为电站m第t时段的发电流量；dm，t为电站m第t时段的弃水流量；Δt为第t时段的小时数；Qn，m，t为区间入库流量；Fm，k，t为电站m第k个直接上游电站出库流量在第t时段形成滞时流量的函数，根据滞时关系进行计算。

b.发电流量约束：

c.电站出力约束：

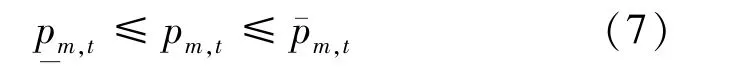
d.库水位约束：

e.出库流量约束：

f.水电总负荷约束：

式中Nt为第t时段的水电负荷。

2 模型求解

设定总负荷过程的水电优化调度问题是具有强系统性约束的非线性优化问题。拉格朗日松弛算法作为常用求解算法之一，具有求解精度高的优点，但其主要难点是需要高效的乘子更新策略。为较合理地评价滞时电量的影响，本文采用拉格朗日松弛法求解模型。

2.1 对偶问题

针对水电系统总负荷约束采用拉格朗日松弛法建立以式（11）为目标函数、以式（4）～（9）为约束条件的对偶优化问题：

式中λt为t时段拉格朗日乘子向量分量。

通过交替进行对偶优化问题求解和乘子更新以实现原问题求解。

2.2 对偶问题求解算法

在约束条件中，水量平衡、发电流量、电站出力约束上限均可以在单时段调节计算中保证满足，水电总负荷约束已经进行了松弛；而库水位约束和出库流量约束二者可以以其中之一的破坏换来另一条件的满足，因此将优先级高者在单时段计算中强制满足，优先级低者采用惩罚函数法处理。本文采用出库流量优先级高于水位控制的策略。剩余约束条件仅有电站出力下限和减少弃水出力，可采用惩罚函数法处理，将式（11）和约束条件式（4）～（9）确定的约束优化问题转换为无约束优化问题：

其中

式中：FP为惩罚函数；为电站m第t时段与水位上下限对应的库容；a1、a2、a3、a4为惩罚系数，需要经过不断测试确定；ps，m，t为电站m第t时段弃水出力。

采用以出库流量为决策变量的逐次逼近单变量搜索算法求解。在每一时段，依次对各电站以定步长将发电流量增加或减小，计算目标函数和惩罚函数值以确定最优决策，并逐步减小搜索步长寻优至达到最小步长限制；而后进行下一时段的计算，待最后一个时段搜索完成后再返回第一个时段，直到收敛。

在以步长Δm对电站m第t时段发电流量qm，t进行搜索计算时，设电站m下游电站标号依次为m +1、m+2、…、m+m′down，其中m′down为电站m下游电站数。首先设qm，t=qm，t+Δm，若qm，t＞q¯m，t，则令qm，t= q¯m，t，保持其余时段出库流量不变，由第t时段开始至第T时段结束进行定发电流量调节计算，若达到水位上限则按照最大发电流量和最大出力进行限制，计算弃水流量。而后计算电站m第t时段出库流达电站m+1的最早可能时段t′，固定电站m+1出库流量过程，由t′起进行定流量调节计算至控制期结束，计算t′时段出库流达电站m+2的可能最早时段。按照同样方法调节，直到最后一级下游电站或者最早流达时间超出控制期，并计算目标函数和惩罚函数值。在qm，t=qm，t-Δm时，调节计算方法类似，而后取初始解和增减流量三者中最优者对应的调度过程并保留。

2.3 两阶段乘子更新策略

按照次梯度法，采用下式进行对偶乘子迭代更新：

式中：λt，i为第i轮次对偶问题求解时的第t时段乘子取值；μt为乘子更新系数，一般μt取值越小，计算精度越高，但迭代次数和计算时间也越长。由于乘子具有比较明确的物理意义，即对应时段单位出力改变造成系统期末蓄能的改变量，对于若干个电站并联组成的系统，其取值可以判断为在单时段的小时数24附近。而对于梯级水电站群，除最上游的龙头电站以外，出力-蓄能改变率之间差异较大，因而初始乘子向量难以直接确定。为保证算法良好的收敛性和计算速度，将乘子的次梯度法更新过程分为两个阶段，可简要概括为：第一阶段中μt只能扩大不能减小以快速求得乘子初始值，第二阶段μt只能减小不能扩大以加速收敛。

a.第一阶段。首先将乘子向量各分量均设置为λt，1=24，计算开始时设定μt=10-3（t=1，2，…，T）。建立对偶问题并采用本文前述算法求解对偶问题，而后再进行乘子更新时，若一轮求解中不发生明显变化则μt加倍。在第i轮次，以下两种情况之一出现，即可固定λt，i在后续轮次的乘子更新时不变，并作为t时段初始乘子值：求解对偶问题前后正负变化；λt，i更新后为0或超过设定的最大可能值。计算至全部时段的乘子都已固定为止。这一阶段在几个轮次内即可结束，由于乘子更新系数可不断扩大直至得到一个较为合理的结果，可以缓解乘子λt，1和更新系数μt初值设置偏差对求解带来的不利影响。

b.第二阶段。以第一阶段计算得到的各λt，i和 μt作为新的初始值。在每次正负变化时，μt减半。若更新后的乘子向量与原向量的距离小于给定精度，则计算结束。在第一阶段中求得的乘子λt，i和更新系数μt距离最终结果值已经比较接近，差距一般不会超过第二阶段开始时的，为避免结果中出现总出力围绕约束值反复振荡的情况，第二阶段在每一次振荡发生后缩小μt的取值，以逐步减小振荡幅度，在加速收敛的同时可提高算法的鲁棒性。

3 实例仿真

澜沧江干流水电基地是我国十三大水电基地之一，其中澜沧江干流云南段长达1 240 km，落差为1178m，规划了14座电站进行梯级开发。鉴于澜沧江干流梯级水电站群开发现状，本文选取中下游已投产的功果桥（900 MW）、小湾（4 200 MW）、漫湾（1670MW）、大朝山（1350MW）、糯扎渡（5850MW）和景洪（1 750MW）共6座梯级水电站作为研究对象。在这6座水电站群中，当流量低于1 000m3/s时，功果桥至小湾平均流达时间为10 h，小湾至漫湾平均流达时间为3 h，漫湾至大朝山平均流达时间为3 h，大朝山至糯扎渡平均流达时间为11 h，糯扎渡至景洪平均流达时间为3 h。

目前，中期水电调度主要采用两种方式：一是根据水库长期控制方式确定调度期末水位，以发电量最大原则计算各电站在调度期内调度过程；二是固定未来几日水电系统日电量过程，以期末蓄能最大原则进行负荷分配，以满足实际电力需求。

本文以周期为10 d的中期计划为例，采用澜沧江干流中下游2014年5月17—26日各电站的实际入库流量数据，分别在考虑滞时和不考虑滞时的情况下，在对入库流量进行区间还原计算的基础上，首先固定各电站末水位，以等出力方式生成各电站的初始解，由逐步优化算法求解发电量最大模型，总出力过程如图1所示；而后固定结果中的总出力，采用拉格朗日松弛法进行蓄能最大模型求解。由于功果桥只具有日调节能力，在计算时可按径流式电站处理，其他电站如小湾和糯扎渡均为季调节以上电站，可直接参与调节计算。为分析滞时电量对调度结果的影响，选择有调节能力的5座电站的计算结果进行分析。图2为分别考虑和不考虑滞时电量时系统相应蓄能过程，各电站计算结果如图3和图4所示。

图1 梯级水电站总出力过程

图2 系统蓄能过程

图3 水位优化计算结果

图4 出力优化计算结果

在计算结果中，整个梯级水电站的蓄能呈逐步下降趋势（图2），但选择不同的目标函数以及是否考虑滞时，各电站的计算结果有较大差异（图3和图4）。在以发电量最大为目标时，上游小湾电站水位逐步下降，下游漫湾、大朝山和景洪全部在初期蓄水，并依次将水位升至最高，充分发挥了龙头电站对下游的补偿作用，而糯扎渡电站水位逐步下降除与末水位控制有关外，也与其具有巨大的调节库容有关，致使上游电站补偿作用不明显。以期末蓄能最大为目标时，是否考虑滞时电量对漫湾、大朝山和景洪电站的计算结果有较大影响，如漫湾电站最后时段降低了发电水头，从而保证更多的水量在控制期内被下游利用。以发电量、滞时电量和期末蓄能三部分之和作为系统水能利用指标进行比较，是否将滞时电量纳入目标函数的结果对比见表1。容易看出，是否考虑滞时电量对发电量最大模型在发电量和滞时电量两个指标方面有一定影响。在将滞时电量纳入系统蓄能最大模型时，总的能量指标提高了0.130亿kW·h。若不考虑滞时电量因素，虽然控制期内电量指标占优，但由于未考虑调度结果后效性，在控制期与其后衔接时段造成水能利用效率降低。可见在梯级上下游距离较远时，梯级滞时电量不能忽略。

表1 水能计算结果对比亿kW·h

仅以考虑滞时电量对本文算法进行分析，采用两阶段次梯度法乘子更新策略的拉格朗日松弛法计算中共进行57次乘子迭代更新。在第一阶段，仅经过8次迭代更新即寻找到全部乘子向量分量新的初始值。在两个阶段衔接处，乘子发生了几次迭代振荡，但因采用更新系数减小的策略，振荡幅度逐步减小并趋于稳定。由于乘子更新的精度问题，结果中总出力过程与设定值有微小偏差，采用负荷逐步分配法修正以保证与设定值吻合。从表1可看出，采用拉格朗日松弛法求解考虑滞时电量的期末蓄能最大模型较发电量最大模型在总的能量指标方面有一定程度提高，因此，拉格朗日松弛法适应用于中期调度计划制定。

4 结语

随着我国水电资源的大规模开发以及大量水电站投入运行，如何更充分合理地利用水能资源成了水电调度领域研究的热点。在梯级水电站群中期优化调度中，当梯级水电站最上游和最下游距离较远时，水流滞时问题不能忽略。本文以中期期末蓄能最大为目标，重点研究了滞时电量对水电系统优化调度的影响，并给出了求解方法。澜沧江中下游已投产梯级水电站群仿真计算结果表明，滞时电量对中期水电调度影响明显，可供梯级水电站群优化运行水平，实现精细化调度参考。

［1］张雯怡，黄强，畅建霞.水库发电优化调度模型的对比研究［J］.西北水力发电，2005，21（3）：47-49.（ZHANG Wenyi，HUANG Qiang，CHANG Jianxia.Comparison of optimal dispatching model for hydropower station［J］.Journal of Northwest Hydroelectric Power，2005，21（3）：47-49.（in Chinese））

［2］梅亚东，杨娜，翟丽妮.雅砻江下游梯级水库生态友好型优化调度［J］.水科学进展，2009，20（5）：721-725.（MEIYadong，YANG Na，ZHAILini.Optimal ecological sound operation of cascade reservoirs in the lower Yalongjiang River［J］.2009，20（5）：721-725.（in Chinese））

［3］YOO JH.Maximization of hydropower generation through the application of a linear programmingmodel［J］.Journal of Hydrology，2009，376（1/2）：182-187.

［4］HINCAL O，ALTAN-SAKARYA A，METINGER A. Optimization ofmultireservoir systems by genetic algorithm［J］.Water Resources Management，2011，25（5）：1465-1487.

［5］WANG J W，YUAN X H，ZHANG Y C.Short-term scheduling of large-scale hydropower systems for energy maximization［J］.Journal of Water Resources Planning and Management，2004，130（3）：198-205.

［6］BRAGA B PF，YEHWW G，BECKER L，etal.Stochastic optimization of multiple-reservoir-system operation［J］. Journal of Water Resources Planning and Management，1991，117（4）：471-481.

［7］YU ZW，SPARROW F T，BOWEN B H.A new long-term hydro production scheduling method for maximizing the profit of hydroelectric systems［J］.IEEE Transactions on Power Systems，1998，13（1）：66-71.

［8］陈森林，万俊，刘子龙，等.水电系统短期优化调度的一般性准则（1）：基本概念与数学模型［J］.武汉水利电力大学学报，1999，32（3）：34-37.（CHEN Senlin，WAN Jun，LIU Zilong，et al.The general principle of short-term optimizaiton dispatching in hydroelectric system（1）：basic conception and mathematical model［J］.Journal of Wuhan University of Hydraulic and Electrical Engineering，1999，32（3）：34-37.（in Chinese））

［9］张双虎，黄强，蒋云钟，等.梯级电站长期负荷分配模型及其求解方法［J］.西安理工大学学报，2009，25（2）：135-140.（ZHANG Shuanghu，HUANG Qiang，JIANG Yunzhong，et al.The model and method of cascade hydroelectric power stations long-term load distribution［J］.Journal of Xi'an University of Technology，2009，25（2）：135-140.（in Chinese））

［10］BARROS M T L，TSAI F T C，YANG S L，et al. Optimization of large-scale hydropower system operations［J］.Journal of Water Resources Planning and Management，2003，129（3）：178-188.

［11］YEH W.Reservoir management and operations models：a state-of-the-art review［J］.Water Resouces Research，1985，21（12）：1797-1818.

［12］杨侃，陈雷.梯级水电站群调度多目标网络分析模型［J］.水利水电科技进展，1998，18（3）：35-38.（YANG Kan，CHEN Lei.Application of multiobjective network analysis model for cascade hydroelectric stations［J］. Advances in Science and Technology ofWater Resources，1998，18（3）：35-38.（in Chinese））

［13］LABADIE JW.Optimal operation ofmultireservoir：state of the art review［J］.Journal ofWater Resources Planning and Management，2004，130（2）：93-111.

［14］徐刚，夏甜.基于改进与优化调度图的梯级电站联合调度［J］.水利水电科技进展，2014，34（3）：44-49.（XU Gang，XIA Tian.Joint dispatching of cascade hydropower station based on improved and optimized reservoir operation chart［J］.Advances in Science and Technology ofWater Resources，2014，34（3）：44-49.（in Chinese））

［15］张阳，钟平安，徐斌，等.基于廊道约束的水库调度图优化遗传算法［J］.水利水电科技进展，2014，34（6）：13-17.（ZHANG Yang，ZHONG Pingan，XU Bin，et al. Optimization of reservoir operation chart based on genetic algorithm using constraintof grid［J］.Advances in Science and Technology ofWater Resources，2014，34（6）：13-17.（in Chinese））

［16］FINARDIE C，da SILVA E L.Solving the hydro unit commitment problem via dual decomposition and sequential quadratic programming［J］.IEEE Transactions on Power Systems，2006，21（2）：835-844.

［17］MAHESWARIS，VIJAYALAKSHMIC.An optimal design to schedule the hydropower generation using lagrangian relaxation method［C］//Proceedings of the International Conference on Information Systems Design and Intelligent Applications.Berlin：Springer，2012：723-730.

［18］程春田，杨凤英，武新宇，等.基于模拟逐次逼近算法的梯级水电站群优化调度图研究［J］.水力发电学报，2010，29（6）：71-77.（CHENG Chuntian，YANG Fengying，WU Xinyu，et al.Link the simulation with dynamic programming successive approximations to the study on optimal operation chartof cascade reservoirs［J］. Journal of Hydroelectric Engineering，2010，29（6）：71-77.（in Chinese））

Lagrangian relaxation method for medium-term operation of hydropower systems considering delayed energy

LI Baojian1，2，WU Xinyu1，SHEN Jianjian1
（1.Institute ofHydropowerand Hydroinformatics，Dalian University of Technology，Dalian 116024，China；2.School ofWater Conservancy，North China University ofWater Resources and Electric Power，Zhengzhou，450045，China）

In view of the problem of inflow delay in medium-term operation of cascade hydropower stations，a concept of delayed energy is introduced，and a stored energymaximization modelwas constructed for the end of the operation period. A Lagrange relaxationmethod based on a two-stage subgradientalgorithm used to updatemultipliers is proposed to solve the model.In the first stage，the initialmultipliers are rapidly determined by increasing coefficients gradually.In the second stage，the convergence speed is increased by decreasing coefficients gradually.The proposed model and solution method were applied tomedium-term optimal operation of six hydropower stations located in the middle and lower reaches of the Lancang River.The results show that the proposed method can obtain good solutions，considering delayed energy can increase stored energy of the hydropower system for the end of the operation period，and the post-effect ofmedium-term operation should be considered sufficiently.

cascade hydropower stations；optimal operation；medium-term operation；stored energymaximization；delayed energy；Lagrange relaxation method

TV697.1+2

1006- 7647（2016）04- 0059- 06

10.3880/j.issn.1006- 7647.2016.04.011

2015- 05 24 编辑：熊水斌）