基于图像的旋翼式水表指针读数自动识别研究

余　坤, 刘明娟, 王凡彬， 何　涛

(1.湖北工业大学现代制造质量工程重点实验室， 湖北 武汉 430068; 2 武汉市水务集团武汉汉水计量科技有限公司，湖北 武汉 430071; 3 湖北省宜昌市知识产权局， 湖北 宜昌 443000)



基于图像的旋翼式水表指针读数自动识别研究

余坤1, 刘明娟2, 王凡彬3， 何涛1

(1.湖北工业大学现代制造质量工程重点实验室， 湖北 武汉 430068; 2 武汉市水务集团武汉汉水计量科技有限公司，湖北 武汉 430071; 3 湖北省宜昌市知识产权局， 湖北 宜昌 443000)

水表指针的读数自动识别，对于水表校准、智能抄表等有重要作用。普通方法识别三角形特点的旋翼式水表指针读数有一定困难。旋翼式水表指针角度的识别方法——双圆心相对测量法，能够准确确定回转圆心位置，通过相对测量点、基准点以及搜索得到的中心点之间的角度关系，最终识别指针读数。实验结果表明：双圆心相对测量方法识别旋翼式水表指针读数，具有很好的准确性、稳定性和实时性。

旋翼式水表； 读数识别； 双圆心相对测量法； 图像处理

普遍家用的旋翼式水表如图1所示，其工作原理是，水流从水表进水口进入表壳冲击叶轮使叶轮开始转动，叶轮转动后，带动叶轮盒内的传动齿轮转动，从而带动刻度盘上的三角指针转动。三角形指针之间以十进位的传递方式相关联，按顺时针的方向进行转动计量。

光电直读技术在检测干燥环境中的仪表读数有成功先例，但是检测潮湿环境中的旋翼式水表读数存在技术缺陷。电压表、气压表、千分表等在干燥环境中的线性单指针仪表，指针目标突出。但是旋翼式水表表盘具有多个三角形指针，且占图像面积小，这些特点使得图像处理过程变得复杂，给识别带来难度。

Alegria[1]对于仪表设备提出利用差影法得到两个不同位置的指针图像，再利用Hough变换得到指针角度。但是针对旋翼式水表的三角形指针而言，利用差影法相减得到的结果图像不同于线性图像，不适合用Hough变换搜索直接得到圆心坐标。

孙凤杰[2]在研究表盘指针角度识别时，提出了基于图像处理技术的电力系统设备指针角度识别方法——同心圆环搜索法，该方法根据表盘指针旋转区域是一个圆形或者圆形一部分的特点，选取该区域的圆心和半径，然后按照一定大小的步长在同心圆环中寻找指针与同心圆环的交点，根据交点之间形成的线段的斜率来识别判断指针相对于零度基准线的角度，这种方法对于刻盘圆心固定的仪表具有一定的可行性。但是旋翼式水表指针旋转时的回转圆心位置并不一定和指针圆盘圆心位置完全一致，此时利用同心圆环搜索法得到的读数结果存在误差。

本文在同心圆搜索法的基础上，结合旋翼式水表指针特点，提出了确定三角形指针回转圆心和计算角度的方法——双圆心相对测量法。该方法通过测量水表刻度盘相对点、基准零点以及利用双圆心相对测量法确定的中心点之间角度关系，计算得出识别角度，能够消除因水表位置微小变化带来的斜率测量误差。该方法进一步提高了对旋翼式水表三角形指针角度的识别精度。

1　水表表盘读数模型

一般旋翼式水表表盘如图2所示。其读数是由一个整数数值N0和四个指针读数数值N1、N2、N3、N4构成，其中N0可以根据字符识别[4]得到，水表读数

N=N0+0.1N1+0.01N2+0.001N3+0.0001N4

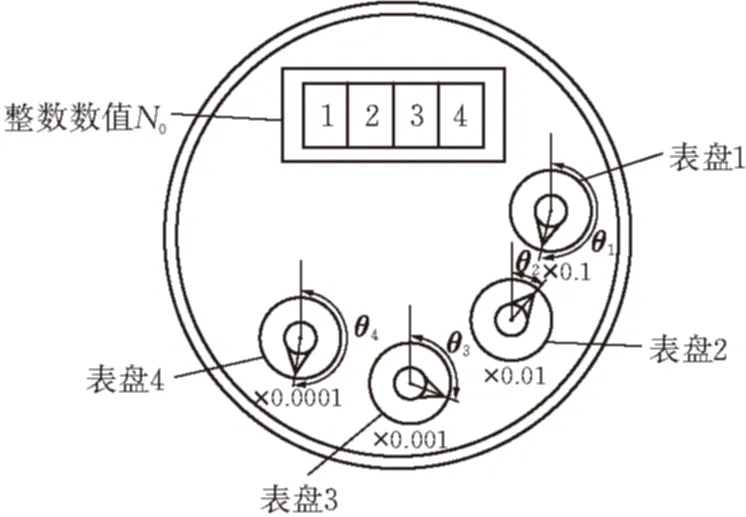
图 2　旋翼式水表表盘读数模型

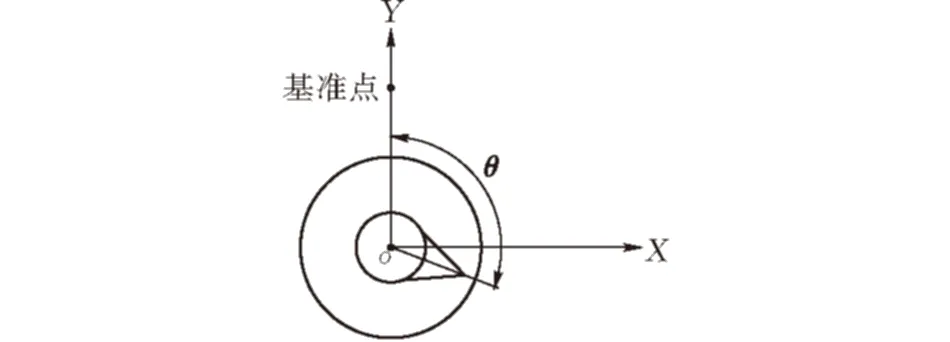
图 3　图3水表指针角度数学模型

假设表盘1～4刻度盘的指针与其各自基准点之间角度分别是θ1、θ2、θ3、θ4，4个指针刻度盘其数量级分别是×0.1、×0.01、×0.001、×0.0001，相邻刻度盘之间满足十进位关系。对于单个刻度盘而言，刻度值0～9将360°刻度圆均分10等份，即每个相邻刻度值之间相差36°。刻盘度读数Ni与角度值θi之间满足数学关系式

Ni=θi/36°

(0≤θi<360°，0≤Ni<10,i=1,2,…)

并且，计算得到Ni值时应该采用去尾法保留整数度数。特别地，当指针出现在临界角0°、36°、72°、108°、144°、180°、216°、252°、288°和324°附近时，为了避免出现较大的读数误差，可以采用文献[3]提出的读数校正方法进行修正，这种临界值读数修正方法可以很好地避免临界值读数误差。

2　双圆心相对测量法模型及算法

2.1双圆心法确定圆心

在研究仪表指针角度识别时，同心圆环搜索法[2]和其他方法默认的前提均是仪表指针围绕固定的回转圆心转动360°或者转动部分圆周角度。但通过大量实验观察，旋翼式水表在工作时其尾圆圆心不是定点。

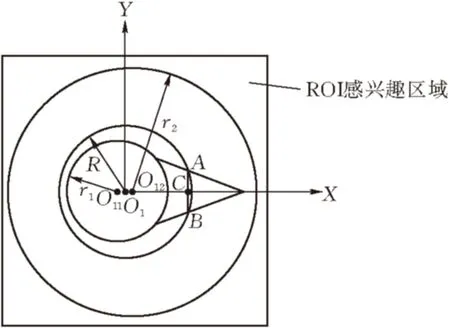
图 4　双圆心法确定圆心模型

本文提出的双圆心法确定回转圆心的模型如图4所示。该方法是在坐标系中，根据预先设定的ROI感兴趣区域，利用Hough算法确定表盘一中指针尾圆圆心O11坐标 、半径r1大小及刻度拟合圆圆心O12坐标、半径r2大小，则在坐标系中由双圆心O11，O12确定的回转圆心O1坐标为

以O1点为圆心，以一定步长R为半径作圆，其中R需要满足

回转圆O1与三角形指针交点记作点A、点B，则由两交点A、B确定的中心点C坐标值为

(1)

则由圆心O1和回转圆与三角形指针交点中点C构成的有向线段O1C代表表盘1的指针位置，进行角度识别。

2.2基于图像的相对点测量算法识别角度算法

旋翼式水表在实际运行中是不允许将指针调整到基准位置进行校准的，因此本文提出一种相对不变点进行测量方法。根据双圆心法可以确定图像中4个表盘的回转圆心在像素坐标下的坐标值，以基准零点、表盘2回转圆心O2、表盘1回转圆心O1和表盘1的三角形指针交点中点C1为例测量表盘1中指针角度数学模型(图5)。

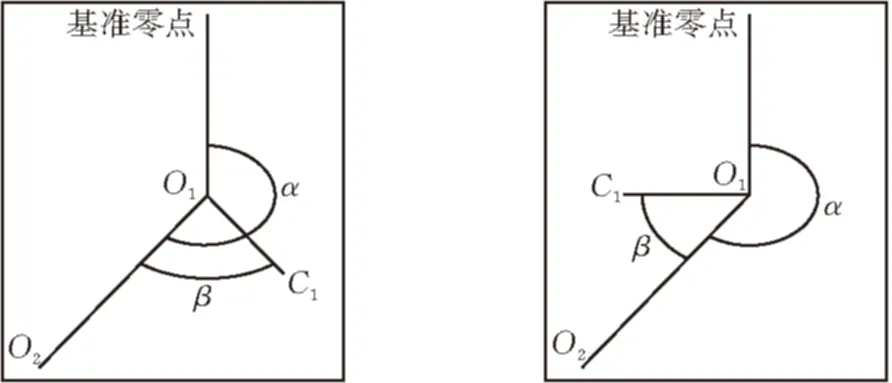
(a)θ=α-β　　　　　　　　　　(b)θ=α+β图 5　相对点测量法测量指针角度

在相机拍摄环境下，旋翼式水表各个表盘回转圆点与基准零点之间的相对位置是不变的，定点与基准零点之间的基准夹角角度α，再通过测量出两定点与指针交点中点C1之间的角度值β。

当角度β与角度α有重合部分时，指针角度

θ=α-β

当角度β与角度α没有重合部分时，指针角度

θ=α+β

(1)

特别地，当点C1在三定点线段上时，指针角度θ可以由式(1)计算得到。

3　图像预处理及结果

旋翼式水表指针角度识别前，需要先对水表图像进行前期处理，其流程如图6所示。

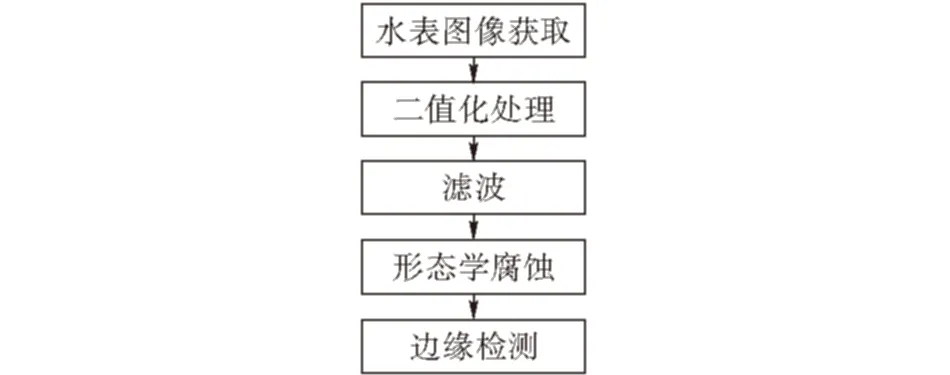
图 6　水表图像前期图像处理流程

在阈值T下将获得的水表图像f(x,y)进行图像二值化和中值滤波之后，得到图像g(x,y)。形态学腐蚀处理可以提取图像骨干信息，去掉毛刺孤立噪声。腐蚀运算由结构元素确定的邻域块中选取图像值与结构元素值的差的最小值。其计算公式是

单像素宽度边界图像对于搜索找到两指针交点A、点B很重要。由于Canny算子提取的边缘质量很高，所以采用Canny算子进行边缘检测。图7为一组水表表盘图像处理前后比对图。

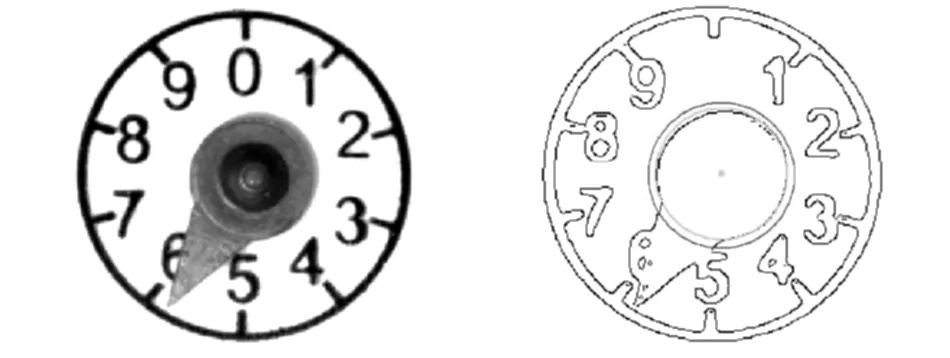
(a)水表表盘图像　　　　　　(b)水表表盘处理后图像图 7　一组水表表盘图像处理前后对比图

选用Basler工业级黑白相机连续采集若干张旋翼式水表工作图像，利用LabVIEW软件编写检测算法前面面板(图8)。

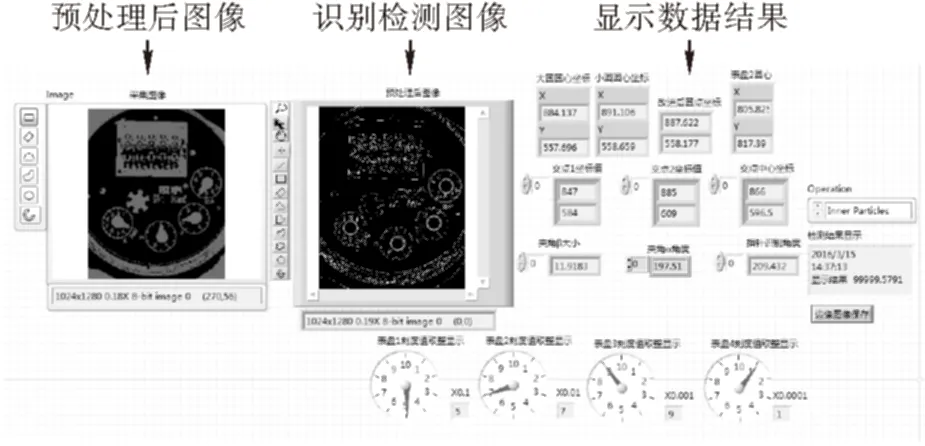
图 8　水表指针角度识别检测LabVIEW软件界面

4　实验结果以及误差分析

表1中，利用双圆心法对20组不同角度情况下的水表指针图像进行识别读数，通过与人工读数比较，发现利用双圆心相对测量法识别20组水表图像指针角度最大误差为2.923°，最大相对误差在4%以内，满足工程指标要求。

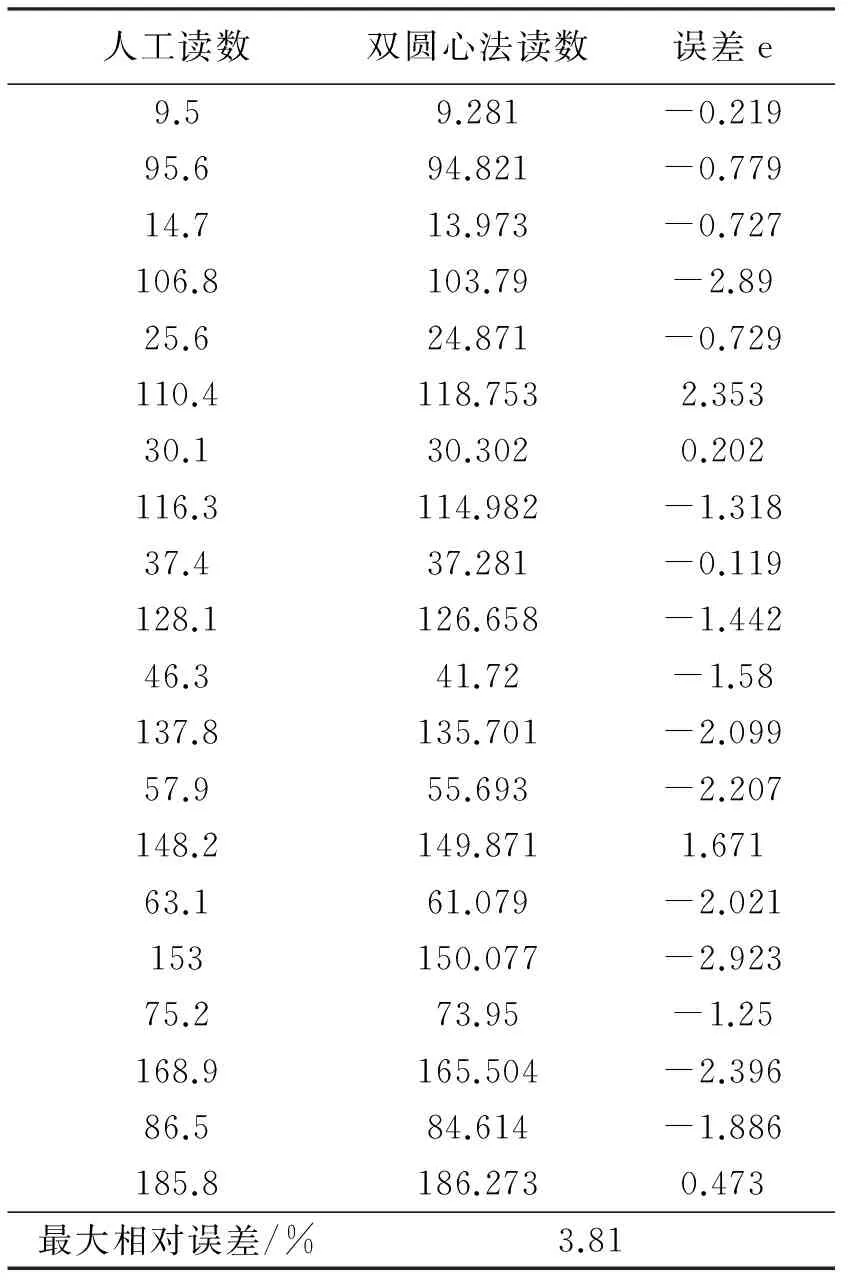
表1　双圆心法与人工读数结果 　(°)

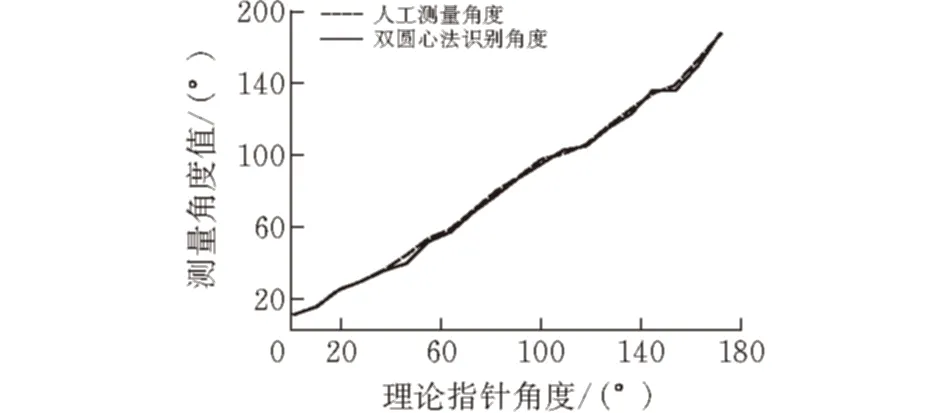
图 9　双圆心法识别读数人工读数结果

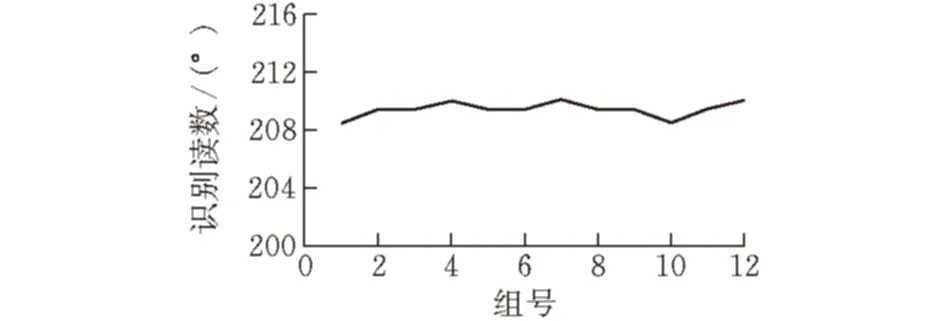
图 10　利用双圆心相对测量法识别不变指针角度结果

为了验证双圆心相对测量法识别水表指针角度的稳定性，对不同时间拍摄的人工读数为209.0°的12张水表图像进行识别，角度识别结果如图9所示。结果表明双圆心相对测量法具有很好的识别稳定性能，识别时间在300 ms以下。

实验中出现的误差与实验环境光强度大小、选取阈值有一定关系。

5　结论

1)双圆心相对测量方法能够识别旋翼式水表指针角度，具有很好的准确性、稳定性和实时性。

2)双圆心相对测量方法对于旋翼式水表指针具有很好的角度识别效果，在仪表设备自动读数研究上具有一定工程应用价值。

[1]Alegria F C, Cruz Serra A. Automatic calibration of analog and digital measuring instruments using computer vision[J]. IEEE Transactions on Instrumentation & Measurement, 2000, 49(1):94-99.

[2]孙凤杰, 郭凤顺, 范杰清,等. 基于图像处理技术的表盘指针角度识别研究[J]. 中国电机工程学报, 2005, 25(16):73-78.

[3]戴亚文, 王三武, 吴小兰. 基于图像的复杂仪表读数识别[J]. 仪表技术, 2003(2):11-12.

[4]卢艳. 基于机器视觉技术的模拟指针式仪表自动检定系统[D]. 重庆：重庆大学, 2004.

[5]王瑞, 李琦, 方彦军. 一种基于改进角度法的指针式仪表图像自动读数方法[J]. 电测与仪表, 2013(11):115-118.

[6]李雄, 裴承鸣, 郑华. 几何特征形态学车牌识别系统研究[J]. 计算机仿真, 2012(4):353-356.

[7]龚雄文. 指针式仪表自动读数的研究及应用[D]. 广州：广东工业大学, 2007.

[责任编校： 张众]

Research on Automatic Identification of Rotor Type Watermeter’s Pointer Based on the Image

YU Kun1, LIU Mingjuan2, WANG Fanbing3, HE Tao1

(1HubeiKeyLabofModernManufactureQualityEngineering,HubeiUniversityofTechnology,Wuhan430068，China; 2HanRiverMeasurementTechnologyCo.Ltd.ofWuhanWaterGroup,Wuhan430071,China; 3IntellectualPropertyofYichang,Yichang443000,China)

Rotor watermeter pointer is composed of triangular tip and nearly circular disc, which is different from ordinary instrumentation pointer with linear characteristics. The rotor type watermeter with ordinary methods encounters certain difficulties in recognizing triangle features. Based on double ring search method, a recognition method of meeting rotor watermeter pointer angle is proposed —— double circle relative measuring method. The method can accurately determine rotation center position, which gets the identification angle through calculating the center that is obtained by searching the relative measurement and the angle relationship between datum. Experimental results show that the double circle relative measurement method is able to identify rotor watermeter pointer angle, which has very good accuracy, stability and real-time performance.

rotor type watermeter；reading recognition; double circle relative measuring method; image processing

2016-05-16

余坤(1992-)， 男， 安徽池州人，湖北工业大学硕士研究生，研究方向为图像处理技术

1003-4684(2016)04-0034-04

TM932

A