考虑微观渗流的页岩气藏拉链式压裂水平井产能预测
2016-10-18蒲谢洋胡永全赵金洲李志强
蒲谢洋,胡永全,赵金洲,李志强
考虑微观渗流的页岩气藏拉链式压裂水平井产能预测
蒲谢洋a,胡永全a,赵金洲b,李志强a
(西南石油大学a.石油与天然气工程学院;b.油气藏地质及开发工程国家重点实验室,成都610500)
在考虑了页岩气多重运移机制的基础上,建立了页岩纳米孔隙气体流动模型和页岩表观渗透率统一模型。
页岩气;拉链式压裂;产能;微观渗流;扩散;改造体积
在世界范围内,页岩气作为非常规能源,具有丰富的资源量和广阔的开采前景。页岩储集层渗透率极低,且通常天然裂缝发育。为了有效开启天然裂缝,增大改造体积,新的压裂模式被应用于页岩气的有效开发中[1]。其中,拉链式压裂利用缝间应力干扰[2],提高了裂缝复杂程度,从而增强了改造效果。
页岩气藏压裂水平井产能预测方法,主要包括数值模拟法和半解析法。文献[3]采用数值模拟法,分析了页岩气压裂水平井产能的影响因素;文献[4]考虑页岩气藏吸附解吸作用,建立了页岩气分段压裂水平井产能半解析模型;文献[5]基于位势叠加原理,建立了分段多簇压裂水平井产能半解析计算模型,分析了压裂水平井产能分布及其影响因素;文献[6]考虑吸附解吸作用,建立了页岩气分段压裂水平井产能模型,分析了天然裂缝和吸附解吸对压裂水平井产能的影响;文献[7]根据双重介质模型,建立了页岩气压裂水平井不稳定渗流模型。页岩基质孔隙尺寸为纳米级,气体流动机理不同于常规储集层[8-9],而已有的页岩气藏压裂水平井产能预测模型,没有全面考虑滑脱效应、努森扩散、表面扩散的页岩微观渗流特征和吸附解吸作用,且关于页岩气藏压裂水平井产能的研究主要集中在分段压裂水平井产能上,对拉链式压裂水平井的产能研究鲜有报道。因此,综合考虑页岩气在纳米级基质孔隙中的微观渗流和压裂裂缝中的宏观渗流特征,建立页岩气藏拉链式压裂水平井产能预测模型,开展相关产能研究,具有重要的理论和实际意义。
笔者在考虑了页岩纳米孔隙气体运移多重机制的基础上,建立了页岩表观渗透率统一模型,并基于压降叠加原理和矩阵变换,建立了页岩气藏拉链式压裂水平井产能预测模型。应用数值迭代算法求解,分析了微观渗流、井间距和改造体积等对拉链式压裂水平井产能的影响。
1 物理模型及其假设条件
拉链式压裂技术的目的在于通过裂缝间应力干扰,改变原地应力场,有效开启天然裂缝,增强改造效果。拉链式压裂井组由3口压裂水平井组成(图1),位于气藏中心,水平井1的裂缝错列位于水平井2和水平井3的裂缝之间。在压裂时,通过先连续压裂水平井2和水平井3的裂缝,形成应力干扰,再压裂水平井1的裂缝,从而增大改造体积(SRV)。为了简化,裂缝系统为双翼对称缝,改造区内和改造区外的页岩基质性质相同。拉链式压裂改造体积及其重叠区如图2所示。
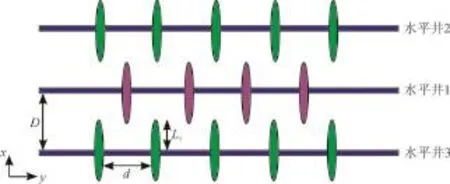
图1 页岩气藏拉链式压裂水平井组
2 数学模型
模型的假设条件为:①页岩气藏为箱形封闭气藏;②垂直方向裂缝完全穿透储集层;③初始气藏压力均匀分布;④水平井筒为无限导流;⑤气藏中为单相气体流动;⑥流体仅通过裂缝流入井筒;⑦不考虑重力的影响。
(1)纳米孔隙气体流动模型页岩纳米孔隙气体运移机制主要包括黏性流、滑移流、努森扩散和表面扩散。其中黏性流质量通量

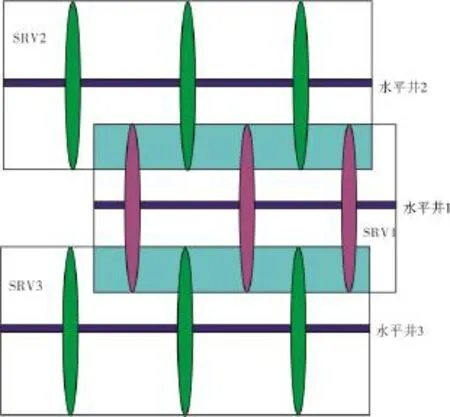
图2 页岩气藏拉链式压裂改造体积及其重叠区
通过滑脱因子对黏性流质量通量修正,得到滑移流质量通量[10]
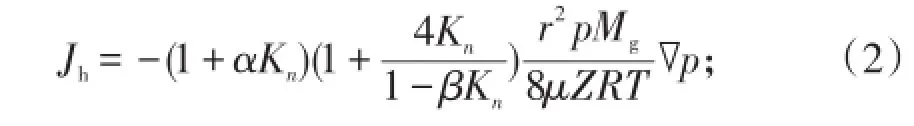
努森扩散质量通量[11]

表面扩散质量通量[12]
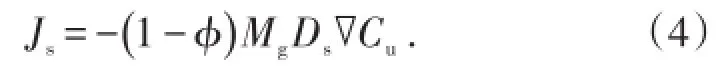
考虑页岩气吸附解吸,由Langmuir等温吸附定律有
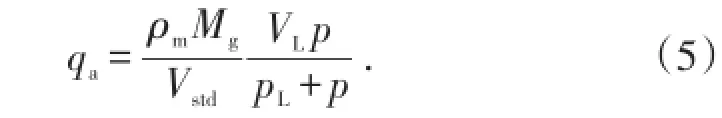
引入加权因子表征滑移流和努森扩散质量通量的贡献率[13],通过叠加滑移流、努森扩散和表面扩散质量通量,可得气体流经页岩纳米孔隙的总质量通量:
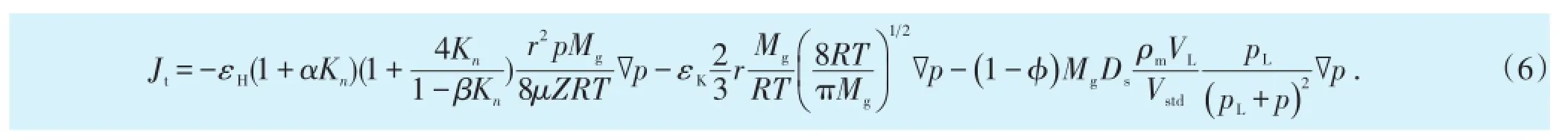
根据达西流动的质量通量表达式,将(6)式改写,可获得考虑微观渗流的页岩表观渗透率
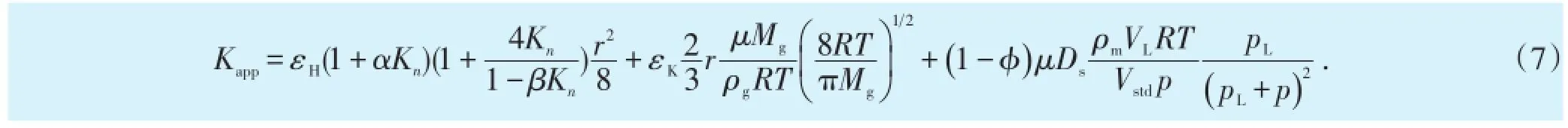
考虑吸附层将导致纳米孔隙减小,有效孔径为[14]
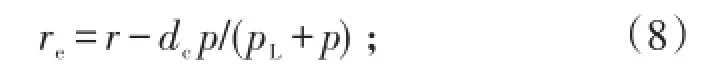
最终可得到考虑孔隙迂曲度的页岩表观渗透率为

(2)气藏渗流模型考虑页岩气藏中为单相气体流动,则页岩气藏渗流可以采用气体扩散方程描述,并可采用瞬时源函数求解气体扩散方程[15]。封闭边界气藏在初始时刻各边界并无流体流动,根据纽曼积分原理,则压裂水平井开始生产时,沿裂缝壁面某点(xi,yi,zi)流入流体对气藏中任意一点(x,y,z)产生的压降为
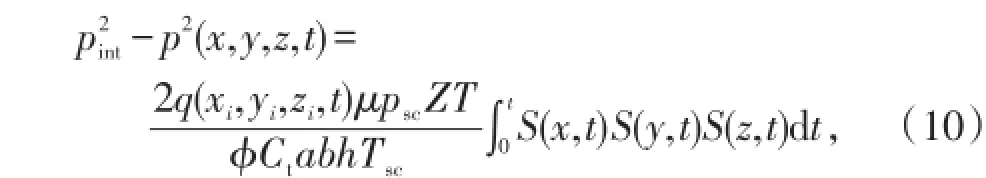
其中
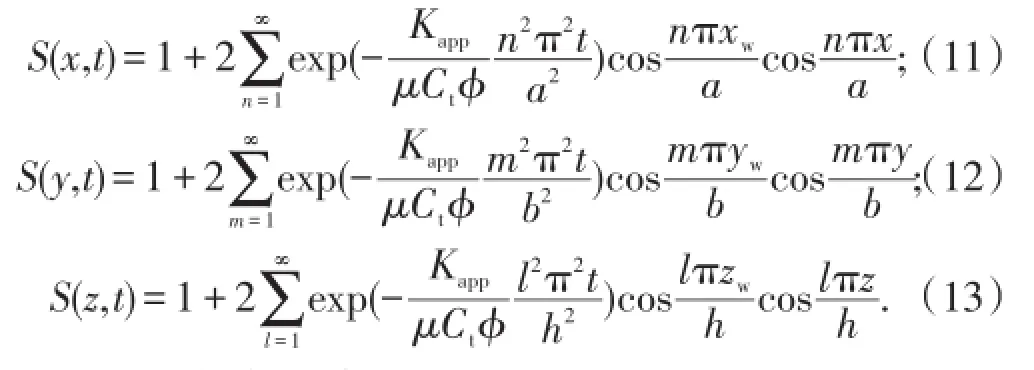
定义气藏压降系数为

对于一个拉链式压裂水平井组,位于中间的水平井压裂N段,外部2口水平井压裂N+1段,将每条裂缝离散为2n份(图3),每翼n份,则一个井组所有压裂裂缝共离散为2n(3N+2)个裂缝网格。每个裂缝网格可视为一个点汇,每份裂缝网格的流入流量为q(m,l,k,j,i,t),(10)式适用于每份裂缝网格,根据压降叠加原理,所有裂缝网格在t时刻对气藏中任意点(x,y,z)产生的总压降为

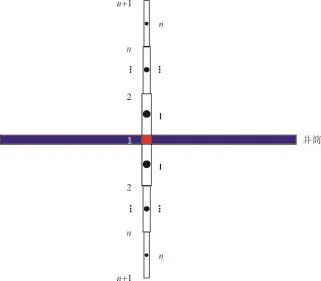
图3 单条裂缝离散示意
(3)裂缝渗流模型假设裂缝内充满了流体,无流体储集现象,根据质量守恒,则对于每个裂缝网格而言,流入流量等于流出流量,即
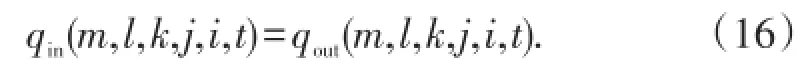
根据裂缝变缝宽形态,对于不同裂缝网格采用不同的宽度值。考虑裂缝内为一维线性流动,且不考虑水平井筒压降,由达西定律可得裂缝中任意点i到井筒的压降为

3 模型求解
由于气藏流体在储集层内流动与在裂缝内流动对裂缝壁面造成的压力相等,则根据(15)式和(17)式,可建立气藏—裂缝—井筒耦合流动方程

模型求解的思路为:第一步求解气藏压降方程的系数矩阵,第二步求解裂缝缝内压降方程的系数矩阵,第三步求解耦合流动方程的系数矩阵,最后通过数值迭代算法求解拉链式压裂水平井组产量。
由(15)式可得拉链式压裂水平井组2n(3N+2)个裂缝网格在t时刻对任一裂缝网格产生的总压降,最终得到2n(3N+2)个线性方程组,将其转化为矩阵形式,可得到2n(3N+2)阶方阵的气藏压降系数矩阵

对于任意离散为n份的单翼裂缝来说,(17)式适用于每个裂缝网格,从而得到n个线性方程组,将其转换为矩阵形式,可得到单翼裂缝缝内压降系数矩阵

其中
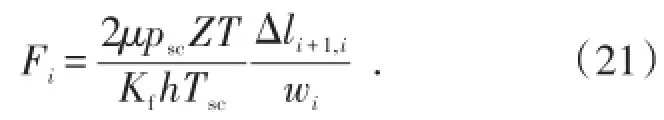
根据拉链式压裂水平井组裂缝网格空间坐标,对单翼裂缝缝内压降系数矩阵块进行组合,可得到6N+ 4阶对角方阵的裂缝缝内压降方程的系数矩阵
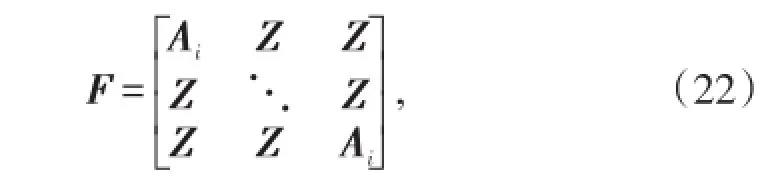
其中,Z为n阶零矩阵。
将(18)式改写成矩阵形式,为

其中

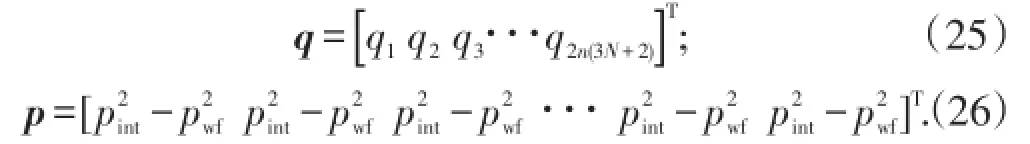
(23)式为线性方程组,通过数值迭代算法即可求解。
4 实例模拟分析
选取某页岩气井基础参数为:页岩气藏长度700 m,宽度500 m,厚度40 m,基质渗透率0.000 1 mD,孔隙度3.5%,原始地层压力20 MPa,气藏温度363 K,气体黏度0.015 mPa·s,综合压缩系数2.3×10-2MPa-1,Langmuir压力5 MPa,Langmuir体积2×10-3m3/kg,页岩密度2 600 kg/m3,气体摩尔质量16 g/mol,页岩平均孔隙半径5 nm,孔隙迂曲度5,表面扩散系数1×10-7m/s2,标准状况下温度273 K,标准状况下压力0.101 3 MPa,井底流压6 MPa,裂缝间距100 m,模拟时间500 d.为减小计算量,在进行模拟计算分析时以一个单元进行计算,即中间水平井压裂一段,外部水平井均压裂两段。
分别采用文献[16]的模型和本文模型计算产能,对模型进行验证。通过精度分析,确定每条裂缝离散为20个网格,本文模型裂缝网格如图4所示。
采用本文模型预测的产量为20.5×104m3/d,文献[16]模型预测的产量为22.6×104m3/d,实际产量为18.7×104m3/d,误差分别为9.6%和20.9%.可见本文模型计算的结果更接近实际产量,准确性较高。
不同页岩纳米孔隙气体运移机制对页岩气藏拉链式压裂水平井产量的贡献如图5所示。单独考虑气体3种不同运移机制影响,按其对产量的贡献大小排序依次为滑移流、表面扩散和努森扩散,贡献比例分别为26%,11%和6%.考虑微观渗流影响的产量比不考虑时的产量高43%,这是由于考虑微观渗流的页岩渗透率比不考虑时的渗透率更大。可见页岩气微观渗流对产量有重要影响,并且全面考虑页岩气多重运移机制的产量比单独考虑一种运移机制的产量大。
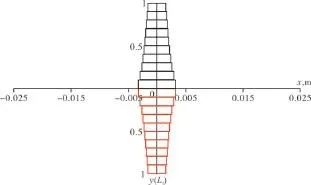
图4 实例计算中本文模型的裂缝离散网格
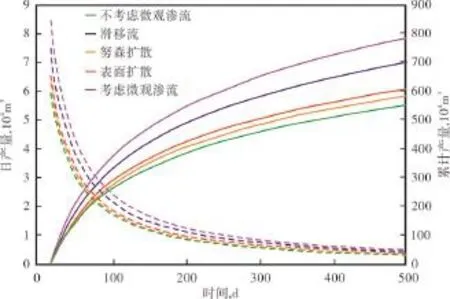
图5 考虑微观渗流和不同运移机制的页岩气产量
不同井间距下拉链式压裂水平井组日产量和累计产量如图6所示。随着井间距的减小,产量逐渐减小,当井间距从300 m减小到260 m,220 m和180 m时,累计产量分别减小5.8%,13.8%和23.7%,且减小的幅度逐渐变大。这是由于在相同的拉链式压裂水平井组数下,随着井间距减小,井间裂缝压力干扰增强,使得有效泄气面积减小。因此对于页岩气藏水平井拉链式压裂,以产量为目标,则存在最优井间距。
页岩气藏水平井拉链式压裂由于采用交错式布缝模式,因此井间存在改造体积重叠的情况。在井间距为300 m时,不同改造体积重叠比例下的产量如图7所示。改造体积重叠对拉链式压裂水平井产量有重要影响,当改造体积重合比例从10%增加到30%,50%和70%时,累计产量分别减小3%,10%和21%,减小程度逐渐增大。这是由于改造体积重叠比例越大,拉链式压裂造成的页岩储集层有效改造体积越小,页岩储集层动用程度减小。因此有效减小改造体积重叠比例,能够提高拉链式压裂水平井产量,存在最优的改造体积重叠比例。
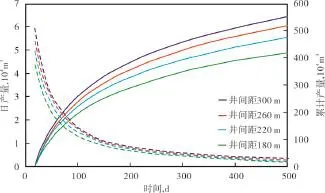
图6 不同井间距的页岩气产量
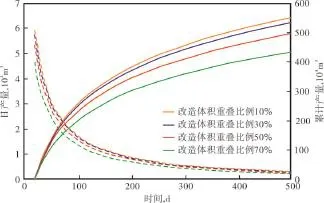
图7 不同改造体积重叠比例下的页岩气产量
5 结论与建议
(1)页岩气微观渗流对拉链式压裂水平井产量有重要影响,考虑微观渗流的累计产量是不考虑微观渗流的1.4倍,不同气体运移机制对产量的贡献大小依次为滑移流、表面扩散和努森扩散,分别为26%,11%和6%.
(2)页岩气藏拉链式压裂水平井井间距越小,产量越小,但并非线性递减关系。产量随井间距增大而增大的幅度逐渐变小,井间距存在最优值。
(3)页岩气藏水平井拉链式压裂的交错式布缝模式导致的改造体积重叠将使产量减小,改造体积重叠比例越大,产量越小,但产量减小的幅度逐渐增大,存在最优的改造体积重叠比例。压裂设计时,在考虑开启天然裂缝的条件下,还应考虑有效减小改造体积重叠比例。
(4)由于本文模型没有考虑天然裂缝的影响和改造区内外页岩储集层性质的差异,笔者建议,在未来的研究中应考虑天然裂缝的影响,并可通过对页岩储集层分区处理来考虑改造区内外页岩储集层性质的差异性。
符号注释
a——页岩气藏长度,m;
b——页岩气藏宽度,m;
Ct——压缩系数,MPa-1;
Cu——吸附气浓度,mol/m3;
D——井间距,m;
Ds——表面扩散系数,m2/s;
d——裂缝间距,m;
dc——气体分子直径,m;
h——页岩气藏厚度,m;
Jh——滑移流质量通量,kg/(m2·s);
Jk——努森扩散质量通量,kg/(m2·s);
Js——表面扩散质量通量,kg/(m2·s);
Jt——总质量通量,kg/(m2·s);
JV——黏性流质量通量,kg/(m2·s);
Kapp——页岩表观渗透率,m2;
Kf——裂缝渗透率,mD;
Kn——努森数,无因次;
Δli+1,i——裂缝网格i+1到裂缝网格i的长度,m;
M——耦合得到的气藏整体压降系数,MPa/m3;
Mg——气体摩尔质量,kg/mol;
p(x,y,z,t)——地层任意点处压力,MPa;
pint——原始地层压力,MPa;
pL——Langmuir压力,MPa;
psc——标准状况下压力,MPa;
pwf——井底流压,MPa;
qa——单位体积页岩气吸附量,m3/kg;
q(m,l,k,j,i,t)——t时刻裂缝网格流入流量,m3/d;
q(xi,yi,zi,t)——t时刻储集层任意点处流入流量,m3/d;
R——气体常数,8.314 J/(mol·K);
R(x,y,z,t)——气藏压降系数,MPa/m3;
r——页岩孔隙半径,m;
re——页岩孔隙有效半径,m;
T——页岩储集层温度,K;
Tsc——标准状况下温度,K;
t——时间,d;
VL——Langmuir体积,m3/kg;
Vstd——标准状态下气体体积,m3/mol;
wj——第j个裂缝网格宽度,m;
xw,yw,zw——点汇坐标,m;
Z——压缩因子,无因次;
α——稀薄气体效应系数,无因次;
β——滑脱因子,无因次;
εH——滑移流加权因子,无因次;
εK——动森扩散加权因子,无因次;
μ——气体黏度,mPa·s;
ρm——页岩密度,kg/m3;
τ——迂曲度,无因次;
φ——孔隙度,无因次。
[1]SOLIMAN M Y,EAST L D,AUGUSTINE J R.Fracturing design aimed at enhancing fracture complexity[R].SPE130043,2010.
[2]RAFIEE M,SOLIMAN M Y,PIRAYESH E.Hydraulic fracturing designandoptimization:amodificationtozipperfrac[R].SPE159786,2012.
[3]YU Wei,ZHANG Tiantian,DU Song,et al.Numerical study of the effect of uneven proppant distribution between multiple fractures on shale gas well performance[J].Fuel,2015,142(1):189-198.
[4]XU Jiancun,GUO Chaohua,WEI Mingzhen,et al.Production performance analysis for composite shale gas reservoir considering multiple transport mechanisms[J].Journal of Natural Gas Science and Engineering,2015,26(3):382-395.
[5]李龙龙,姚军,李阳,等.分段多簇压裂水平井产能计算及其分布规律[J].石油勘探与开发,2014,41(4):457-461.LI Longlong,YAO Jun,LI Yang,et al.Productivity calculation and distribution of staged multi-cluster fractured horizontal wells[J].Petroleum Exploration and Development,2014,41(4):457-461.
[6]曾慧,姚军,樊冬艳,等.页岩气藏分段压裂水平井产能影响因素分析[J].新疆石油地质,2014,35(3):324-328.ZENG Hui,YAO Jun,FAN Dongyan,et al.Analysis of influencing factors about multi-stage fractured horizontal well productivity in shale gas reservoir[J].Xinjiang Petroleum Geology,2014,35(3):324-328.
[7]樊冬艳,姚军,孙海,等.页岩气藏分段压裂水平井不稳定渗流模型[J].中国石油大学学报(自然科学版),2014,38(5):116-123. FAN Dongyan,YAO Jun,SUN Hai,et al.Transient flow model of stage-fractured horizontal wells in shale gas reservoirs[J].Journal of China University of Petroleum(Edition of Natural Science),2014,38(5):116-123.
[8]FREEMAN C M.A numerical study of microscale flow behavior in tight gas and shale gas[R].SPE 141125,2010.
[9]杨峰,宁正福,胡昌蓬,等.页岩储层微观孔隙结构特征[J].石油学报,2013,34(2):301-311. YANG Feng,NING Zhengfu,HU Changpeng,et al.Characterization of microscopic pore structures in shale reservoirs[J].Acta Petrolei Sinica,2013,34(2):301-311.
[10]WUKeliu,CHENZhangxin,LIXiangfang.Realgastransportthrough nanopores of varying cross-section type and shape in shale gas reservoirs[J].Chemical Engineering Journal,2015,281(24):813-825.
[11]WU Keliu,LI Xiangfang,WANG Chenchen,et al.Apparent permeability for gas flow in shale reservoirs coupling effects of gas diffusion and desorption[R].SPE 1921039,2014.
[12]WASAKI A,AKKUTLU I Y.Permeability of organic-rich shale[R].SPE 170830,2014.
[13]WU Keliu,LI Xiangfang,GUO Chaohua,et al.Adsorbed gas surface diffusion and bulk gas transport in nanopores of shale reservoirs with real gas effect-adsorption-mechanical coupling[R].SPE 173201,2015.
[14]SINGH H,JAVADPOUR F,ETTEHADTAVAKKOL A,et al.Nonempirical apparent permeability of shale[J].SPE Reservoir Evaluation&Engineering.2014,17(3),414-424.
[15]GRINGARTEN A C,RAMEY H J.The use of source and green's functions in solving unsteady-flow problems in reservoirs[J].Society of Petroleum Engineers Journal,1973,13(5):285-296.
[16]赵金洲,李志强,胡永全.考虑页岩储层微观渗流的压裂产能数值模拟[J].天然气工业,2015,35(6):53-58. ZHAO Jinzhou,LI Zhiqiang,HU Yongquan.Numerical simulation of productivity after fracturing with consideration to micro-seepage in shale reservoirs[J].Natural Gas Industry,2015,35(6):53-58.
(编辑顾新元)
Productivity Prediction of Zipper-Like Fracturing Horizontal Wells in Shale Gas Reservoirs with Considering Microscopic Flow
PU Xieyanga,HU Yongquana,ZHAO Jinzhoub,LI Zhiqianga
(Southwest Petroleum University a.School of Petroleum&Natural Gas Engineering;b.State Key Laboratory of Reservoir Geology& Exploitation,Chengdu,Sichuan 610500,China)
On the basis of considering multiple migration mechanisms,a nano-pores gas flow model and an apparent-permeability model are established for shales,based on which a gas reservoir-fracture-wellbore coupled flow model is established through fracture space dispersion and by means of pressure drawdown superposition principle,and matrix analysis method and numerical iteration method are used to solve the model.The factors influencing the productivity of zipper-like fracturing horizontal wells in shale gas reservoirs are analyzed by the model.The result shows that the production considering the microscopic flow of shale gas is higher than that without considering the microscopic flow.Slipping flow contributes the most to the gas production with the secondary of surface diffusion and Knudsen diffusion makes the minimum contribution.The incremental gas production gradually decreases with the increase of well spacing,and there is an optimal value of well spacing.The larger the overlap ratio of stimulated reservoir volume is,the less the gas production will be,but there is an optimal overlap ratio of stimulated reservoir volume with the gradual increase of amplitude of gas production decrease.
shale gas;zipper-like fracturing;productivity;microscopic flow;diffusion;stimulated reservoir volume
TE375
A
1001-3873(2016)05-0565-06DOI:10.7657/XJPG20160512
2016-04-24
2016-07-11
国家自然科学基金(51490653)
蒲谢洋(1991-),男,四川渠县人,硕士研究生,油气田增产改造,(Tel)18782949909(E-mail)1137060487@qq.com
在此基础上,通过对裂缝空间离散,应用压降叠加原理,建立了气藏—裂缝—井筒耦合流动模型,并采用矩阵分析方法和数值迭代算法对模型求解。模拟分析了页岩气藏拉链式压裂水平井产能影响因素,结果表明,考虑页岩气微观渗流的产量比不考虑微观渗流的产量高,滑移流对产量的贡献最大,其次为表面扩散,努森扩散贡献最小。产量随井间距增大而增大的幅度逐渐变小,井间距存在最优值。改造体积重叠比例越大,产量越小,但产量减小的幅度逐渐增大,存在最优的改造体积重叠比例。
