体积绝热指数对嘴流流量计算的影响
2016-10-18王发清杨淑珍曹献平陈德非
王发清,杨淑珍,曹献平,陈德非,秦 汉
体积绝热指数对嘴流流量计算的影响
王发清,杨淑珍,曹献平,陈德非,秦汉
(中国石油塔里木油田分公司油气工程研究院,新疆库尔勒841000)
油气田生产上常需计算嘴流流量,其计算方程中的体积绝热指数通常用常数1.3.事实上,嘴流流量计算应使用以温度和压力为函数的体积绝热指数,只有在低压时才能看作是常数。通过分析温度和压力对体积绝热指数的影响认为,当入口压力小于10 MPa时,体积绝热指数可以看作常数;当入口压力大于10 MPa且出口与入口压力比小于0.9时,比热比与体积绝热指数相差较大,不能代替体积绝热指数;相同温度和压力下,同一尺寸油嘴的干气嘴流流量大于凝析气,且凝析油含量越高,凝析气流量越低。
嘴流流量;体积绝热指数;油嘴;节流;比热比
自喷井和气举井在井口安装油嘴,分别用于节流控制产量和注气量,实现对生产动态的调控。除了井口的油嘴外,油田上还有其他许多节流装置,比如井下节流阀、气举阀、分层注气的气嘴等[1-5]。流体通过这些截面突缩部件的流动被称为嘴流。气体嘴流流量方程与绝热指数有关,只有当气体压力较低时,可以当作理想气体,这时绝热指数是定压比热容与定容比热容的比值,为常数;而气体的定压比热容和定容比热容都是温度和压力的函数,这两者的比值被称为比热比。对于气体绝热等熵过程,计算温度相关量时需要使用温度绝热指数;计算体积相关量时需要使用体积绝热指数,两者不相等。气体嘴流流量方程中的绝热指数实际上是体积绝热指数,是温度和压力的函数[6]。油田生产中进行气体嘴流流量计算时,体积绝热指数一般取常数1.3,在温度和压力较高时是不合适的。本文计算了油田常见温度和压力下的气体体积绝热指数,分析了体积绝热指数对气体嘴流流量计算的影响。
1 气体嘴流流量方程
气体的嘴流过程可视为一个绝热等熵的过程,根据流体力学和热力学理论,可以得到嘴流流量方程。
当气体的流速达到声速时,为临界流动状态;当气体的流速小于声速时,为亚临界状态。当出口、入口的压力关系满足(1)式时,达到临界状态[8-9]。

气嘴亚临界状态和临界状态的流量计算公式分别为[4-5]:
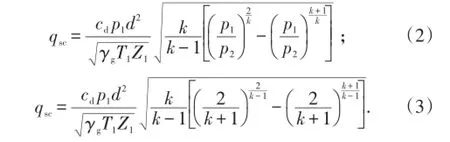
高温高压状态时,绝热等熵过程的状态参数是温度和压力的函数,不再是常数。根据计算用途的不同,分为温度绝热指数和体积绝热指数。计算气体嘴流流量需要使用体积绝热指数,对于绝热等熵过程,压力与密度有如下关系[10]:

2 体积绝热指数计算方法
根据热力学理论,可以推导出体积绝热指数与热力学参数之间的关系[10-11]:

其中,Zp=Z-p(∂Z/∂p)T,ZT=Z+T(∂Z/∂T)p.
从(5)式可看出,计算体积绝热指数需要计算定压比热容、偏差因子及其对温度、压力的偏导数。这些参数的具体计算方法见文献[14]。
Zp和ZT可以通过实际气体的状态方程求得。常用的实际气体状态方程有PR,RKS,BWRS等。本文采用RKS方程,其具体内容参见文献[14]和文献[15]。
3 不同温度、压力下的体积绝热指数和比热比
采用塔里木油田干气井(A井)的组分(氮气1.184%,二氧化碳0.339%,甲烷97.847%,乙烷0.568%,丙烷0.022%,正丁烷0.004%,异丁烷0.009%,正戊烷0.006%,异戊烷0.007%,己烷0.013%,庚烷0.001%),计算了不同温度和压力下的体积绝热指数(图1)和比热比(图2)。
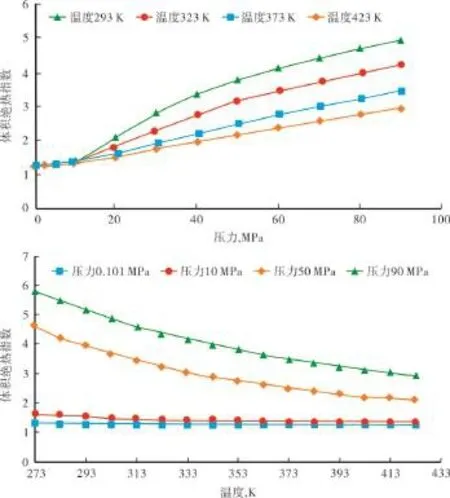
图1 温度和压力对体积绝热指数的影响

图2 温度和压力对比热比的影响
从图1可看出,在油田常见温度范围内,当压力小于10 MPa时,体积绝热指数变化不大,为1.3左右,这与一般文献中的体积绝热指数的取值是符合的;当压力高于10 MPa以后,体积绝热指数随着压力的增加而增大,随着温度的升高而降低,常温时能达到5.0以上,高温时能达到3.0.因此,体积绝热指数是一个变化较大的值,文献中常取1.3,这个值在低压范围是合适的,但是当压力较高时,误差非常大。造成这种现象的原因,是由于气体处于低压时,分子间距离大、分子间作用力小,可以视为理想气体的缘故。
从图2可看出,比热比随着压力的升高先增大,达到一个极大值后开始减小;随温度的升高而减小,这一点与体积绝热指数类似。同时可以看到,当压力较低时,比热比与体积绝热指数接近,也在1.3左右;而当压力较大时,比热比与体积绝热指数相差较大,因此不能用比热比代替体积绝热指数。
4 体积绝热指数对嘴流流量的影响
利用塔里木油田A井的干气组分数据,假设流量系数cd取0.408,嘴孔直径5 mm,计算了不同温度、压力下。当出口与入口压力之比从0变化到1时的气体流量,计算结果见图3和图4.其中固定体积绝热指数为常数1.3.当压力较低,小于10 MPa(如2 MPa),利用本文方法计算出的体积绝热指数计算嘴流流量,与取绝热指数1.3的计算结果差别不大(图3);当入口端压力大于10 MPa(如50 MPa),出口与入口压力比小于0.9时,两者计算结果相差非常大,且温度越低,相差越大(图4);当出口与入口压力比大于0.9时,两者计算结果相差不大。入口压力50 MPa,温度293 K时,两者计算结果相差29%;入口压力50 MPa,温度373 K时,两者相差20%.因此,入口压力较高时,必须根据入口端温度和压力计算体积绝热指数。
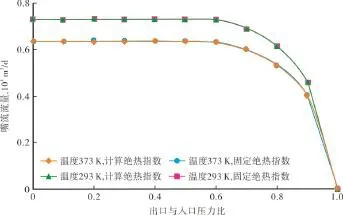
图3 入口压力2 MPa时嘴流流量对比
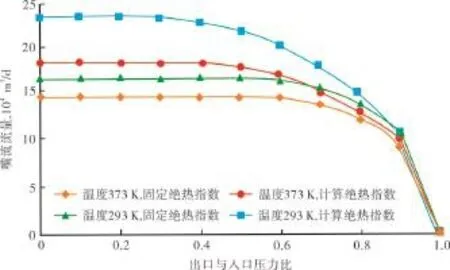
图4 入口压力50 MPa时嘴流流量对比
5 气体组分对嘴流流量的影响
取入口压力50 MPa,温度373 K,嘴孔直径5 mm,分别计算了干气、低含凝析油凝析气和高含凝析油凝析气(表1)的嘴流流量。
当入口温度、压力均相同时,凝析气的嘴流流量低于干气,且凝析油含量越高,嘴流流量越低(图5)。这说明,由于凝析油占据了一定的流动通道,导致凝析气井的嘴流流量低于干气。

表1 塔里木油田3种气体的组分%
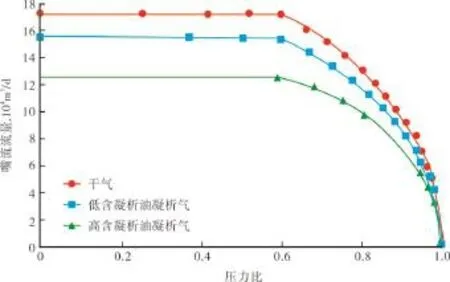
图5 入口压力50 MPa时不同组分的嘴流流量
6 结论
(1)针对目前油气田工程上计算气体嘴流流量时使用绝热指数上存在的问题,提出嘴流流量计算应该使用体积绝热指数,介绍了体积绝热指数的计算方法,并分析了压力、温度对体积绝热指数,对比了体积绝热指数对嘴流流量的影响。
(2)体积绝热指数随温度的升高而降低,随压力的增加而增加。当压力小于10 MPa时,体积绝热指数可视为常数1.3;当压力大于10 MPa时,如果出口与入口压力比大于0.9,工程上体积绝热指数取1.3的固定值是合适的,否则,比热比与体积绝热指数相差较大,用其代替体积绝热指数会带来较大的误差。
(3)当入口温度和压力相同时,干气的嘴流流量高于凝析气。
符号注释
cd——与雷诺数和气嘴形状有关的流量系数,文献[9]中取0.408;
cp——定压比热容,kJ/(kmol·K);
d——孔嘴直径,mm;
k——气体绝热指数;
kV——体积绝热指数;
p2——油嘴出口压力,MPa;
p1——油嘴入口压力,MPa;
qsc——标准状态流量,104m3/d;
R——普适气体常量,8.31 KJ/(kmol·K);
T1——入口温度,K;
Z1——入口气体偏差因子;
ρ1,ρ2——分别为入口和出口的气体密度,kg/m3;
γg——天然气与空气的分子量比,无量纲。
[1]刘花军,王志清,黄春燕,等.分层注汽工艺技术的研究应用[J].石油地质与工程,2007,21(3):79-81. LIU Huajun,WANG Zhiqing,HUANG Chunyan,et al.Researchand application of separate layer steam injection technology[J].Petroleum Geology and Engineering,2007,21(3):79-81.
[2]冯勇,赵金省,何妮娟,等.稠油分层注汽技术及其应用[J].石油化工应用,2009,28(3):59-62. FENG Yong,ZHAO Jinsheng,HE Nijuan,et al.Separate layer steam injection technology and application[J].Petrochemical Industry Application,2009,28(3):59-62.
[3]雷标.一种测量理想气体绝热指数的简易方法[J].河南科学,2012,30(8):1 017-1 019. LEI Biao.A simple method of ideal gas adiabatic exponent measurement[J].Henan Science,2012,30(8):1 017-1 019.
[4]曹明强,张扬,杨国安.压缩机不同转速下性能参数随流量变化研究[J].化工机械,2015,42(2):172-175. CAO Mingqiang,ZHANG Yang,YANG Guo'an.Performance parameter varying with flow under different compressor speeds[J].Chemical Engineering&Machinery,2015,42(2):172-175.
[5]董超群,梁政,田家林,等.天然气压缩机气体多变指数的确定[J].压缩机技术,2013,51(3):7-10. DONG Chaoqun,LIANG Zheng,TIAN Jialin,et al.Determination of air polytropic exponent for natural gas compressor[J].Compressor Technology,2013,51(3):7-10.
[6]李更来,陈红梅.气体绝热指数的计算方法[J].油气田地面工程,1997,16(5):15-16. LI Genglai,CHEN Hongmei.Computation method of natural gas adiabatic exponent[J].Oil-Gas Filed Surface Engineering,1997,16(5):15-16.
[7]蒋代君,陈次昌,钟孚勋,等.天然气井下节流临界状态的判别方法[J].天然气工业,2006,26(9):115-117. JIANG Daijun,CHEN Cichang,ZHONG Fuxun,et al.Discriminance of the flow state in downhole choke of natural gas wells[J]. Natural Gas Industry,2006,26(9):115-117.
[8]李颖川.采油工程(第二版)[M].北京:石油工业出版社,2009:43-58. LI Yingchuan.Oil recovery engineering(2nd edition)[M].Beijing:Petroleum Industry Press,2009:43-58.
[9]李士伦.天然气工程(第二版)[M].北京:石油工业出版社,2008:132-134. LI Shilun.Natural gas engineering(2nd edition)[M].Beijing:Petroleum Industry Press,2008:132-134.
[10]李玉星,姚光镇.输气管道设计与管理[M].山东东营:中国石油大学出版社,2009:50-70. LI Yuxing,YAO Guangzheng.Natual gas pipeline design and management[M].Dongying,Shandong:China Unversity of Petroleum Press,2009:50-70.
[11]朱明善,刘颖,林兆庄,等.工程热力学[M].北京:清华大学出版社,1995:259-263. ZHU Mingshan,LIU Ying,LIN Zhaozhuang,et al.Engineering thermodynamics[M].Beijing:Tsinghua University Press,1995:259-263.
[12]童景山.流体热物性学[M].北京:中国石化出版社,2008:142-147. TONG Jingshan.Fluid thermodynamics[M].Beijing:China Petrochemical Press,2008:142-147.
[13]李长俊.天然气管道输送(第二版)[M].北京:石油工业出版社,2008:41-44. LI Changjun.Natural gas pipeline transmission(2nd edition)[M]. Beijing:Petroleum Industry Press,2008:41-44.
[14]刘晖.实际气体温度绝热指数和容积绝热指数的计算[J].石油化工高等学校学报,2000,13(4):42-45. LIU Hui.Calculation of the isentropic temperature change exponent and isentropic volume change exponent of real gases[J].Journal of Petrochemical Universities,2000,13(4):42-45.
[15]郝敏,陈保东.RKS方程在天然气热物性计算中的应用[J].油气储运,2003,22(10):22-27. HAO Min,CHEN Baodong.The application of RKS equation in calculating thermo-physical properties of natural gas[J].Oil and Gas Storage and Transport,2003,22(10):22-27.
(编辑顾新元)
Impact of Volumetric Adiabatic Exponent on Calculation of Choke Flow Rate
WANG Faqing,YANG Shuzhen,CAO Xianping,CHEN Defei,QIN Han
(Research Institute of Petroleum Engineering,Tarim Oilfield Company,PetroChina,Korla,Xinjiang 841000,China)
Choke flow rate is often needed to be calculated during oil and gas field production and the volumetric adiabatic exponent used as a constant in the calculation is often assumed to be 1.3.In fact,the volumetric adiabatic exponent as a function of temperature and pressure should be used for choke flow rate calculation,and the exponent can be considered as a constant only under the conditions of low pressure.Based on the analysis of the impact of temperature and pressure on the exponent,it is concluded that the volumetric adiabatic exponent can be considered as a constant when the inlet pressure is lower than 10 MPa.When the inlet pressure is more than 10 MPa and outlet to inlet pressure ratio is less than 0.9,there is a big difference between the specific heat ratio and the volumetric adiabatic exponent,so the specific ratio can’t substitute the exponent.Under the same pressure and temperature,dry gas flow rate is larger than condensate gas flow rate from chokes of same size.The higher the condensate content is,the lower the gas flow rate will be.
choke flow rate;volumetric adiabatic exponent;choke;throttling;specific heat ratio
TE319
A
1001-3873(2016)05-0561-04DOI:10.7657/XJPG20160511
2015-12-10
2016-05-19
王发清(1975-),男,湖北孝感人,高级工程师,采油工艺,(Tel)13119960992(E-mail)wangfq-tlm@petrochina.com.cn
