钢管混凝土柱脚节点抗冲切计算分析

卜永红，王毅红，颜卫亨，孙珊珊

（长安大学建筑工程学院，陕西西安710061）

钢管混凝土柱脚节点抗冲切计算分析

卜永红，王毅红，颜卫亨，孙珊珊

（长安大学建筑工程学院，陕西西安710061）

基于8个钢管混凝土柱脚节点在竖向荷载作用下的试验数据，采用理论分析与数据拟合的方法给出该类埋入式柱脚节点较为准确的抗冲切承载力计算公式；基于钢管混凝土柱脚节点在竖向荷载作用过程中表现出的典型特征，数值拟合了三折线结构受力模型，并与试验结果进行了对比。研究结果表明，由拟合的结构受力模型确定的曲线与试件的试验曲线吻合较好，直接反映了试件的受力破坏过程，可应用于钢管混凝土柱脚结构在竖向荷载作用下的非线性反应分析与设计计算。

钢管混凝土柱；柱脚节点；冲切；结构受力模型；设计计算

埋入基础梁的钢管混凝土柱脚节点具有整体性好、抗震能力强的优点，但由于钢管混凝土柱埋入钢筋混凝土基础梁，使得基础梁的有效受力截面高度减小。当钢管混凝土柱在基础梁中的埋置深度较大时，节点区在柱的竖向压力作用下，很容易发生冲切破坏［1］。

文献［2-3］从实际工程中选取试验模型，通过试验研究在钢管混凝土柱脚上设置栓钉、抗剪环、加强环板等措施，取得了提高柱脚节点抗冲切能力的实际效果。本文基于试验研究结果，给出了该类节点较为准确的抗冲切承载力计算公式，并基于钢管混凝土柱脚节点在竖向荷载作用过程中表现出的典型特征，数值拟合了此类节点的结构受力模型。

1　试验概况

按1∶6缩尺比例，设计了8个柱脚节点试件，试件ZJ/J-1和ZJ/J-2均未采取抗冲切加强措施，而在试件ZJ/J-3和ZJ/J-4的柱脚上设置栓钉，在试件ZJ/J-5和ZJ/J-6的柱脚上设置钢筋环箍，在试件ZJ/J-7和ZJ/J-8的柱脚上设置外加强环板，具体的试验设计方案、试验过程、破坏形态等相关内容见文献［2］。

2　节点抗冲切计算分析

2.1节点抗弯、抗剪、抗冲切承载力计算

节点可能的破坏模式包括正截面弯曲破坏、斜截面剪切破坏和核心区冲切破坏。根据《混凝土结构设计规范》（GB 50010—2010），抗弯承载力Mu计算公式为

式中：α1为受压区混凝土矩形应力图的应力值与混凝土轴心抗压强度设计值的比值；fc为混凝土轴心抗压强度；b为基础梁宽度；h0为基础梁截面有效高度；ξ为相对受压区高度；p为试件的竖向承载力；l为支座间的距离。

抗剪承载力V计算公式为

式中：Vc为混凝土抗剪承载力；Vs为箍筋抗剪承载力；h为基础梁高度；ft为混凝土轴心抗拉强度；n为受剪箍筋的根数；fy为箍筋屈服强度；Asv为单根箍筋截面面积。

抗冲切承载力公式中混凝土按45°冲切角计算冲切面积，抗冲切承载力F计算公式为

式中：F1为混凝土的抗冲切承载力；F2为处于冲切范围箍筋的抗冲切承载力；As为按45°冲切角计算的混凝土抗冲切截面面积。

根据材料的实测强度值，结合公式计算各节点抗弯、抗剪、抗冲切承载力理论计算值，见表1。

2.2节点抗冲切计算公式准确性分析

由表1可知：

1）试件ZJ/J-1，ZJ/J-2按试验设计方案未采取抗冲切措施，其抗冲切作用由下环板以下范围的钢筋与混凝土承担，抗冲切承载力较小。节点极限荷载试验值大于节点抗冲切承载力计算值，而小于抗弯与抗剪承载力计算值，表明抗冲切破坏公式偏于保守。

2）试件ZJ/J-3，ZJ/J-5，ZJ/J-7采用3种较强的抗冲切措施，其抗冲切作用由最上部栓钉、抗剪环及外加强环板以下范围的钢筋与混凝土承担，抗冲切承载力较大。节点极限荷载试验值小于节点抗冲切承载力计算值，而大于抗剪承载力计算值，表明其发生剪切（压）破坏。

3）试件ZJ/J-4，ZJ/J-6，ZJ/J-8抗冲切作用的栓钉、抗剪环及外加强环板相比试件ZJ/J-3，ZJ/J-5，ZJ/J-7的设置高度降低许多，数量较少，处于冲切范围的钢筋与混凝土面积较小，抗冲切承载力介于试件ZJ/J-3，ZJ/J-5，ZJ/J-7与试件ZJ/J-1，ZJ/J-2之间。节点极限荷载试验值稍大于抗冲切承载力计算值，而小于抗剪承载力计算值，表明抗冲切承载力公式有些保守；ZJ/J-7极限承载力与ZJ/J-8的极限承载力很接近，这表明外加强环板抗冲切作用较强，使得节点抗冲切承载力大幅提高，从而发生剪切（压）破坏。

2.3节点抗冲切计算公式修正

文献［2］对影响钢管混凝土柱脚节点抗冲切承载能力的因素进行了分析，本文根据分析结果对节点的抗冲切承载力计算公式进行修正，考虑如下因素：

1）梁底部纵筋的作用。在竖向荷载作用下，混凝土基础梁的斜裂缝穿过梁底部钢筋，由于钢筋的销栓作用，可以抑制混凝土梁斜裂缝的开展，所以混凝土梁底部纵筋对节点核心区的抗冲切作用贡献很大。

2）埋入段钢管外壁与混凝土的黏结力。按照文献［4］的钢管与混凝土黏结力计算方法进行计算。

节点抗冲切承载力F修正公式为

式中：F3为梁底部纵筋抗剪作用力；F4为埋入段钢管外壁与混凝土的黏结力；fcu为混凝土立方体抗压强度；d为钢管外直径；h1为钢管埋入深度；a为梁底部纵筋抗冲切作用系数（经试验回归分析取0.1）；fv为梁底部纵筋抗剪强度；A's为梁底部纵筋总面积。

各节点采用修正公式计算的抗冲切理论计算值参见表1。结果表明，修正公式理论计算结果与试验结果能够较好地相互验证。

表1　试验值与理论计算值

3　节点抗冲切结构受力模型

3.1结构受力模型简化

根据试验结果，将试件的水平极限荷载点（pm，Δm）作为试件受力模型无量纲化的基准点，对试件的荷载-位移曲线进行无量纲化（荷载无量纲化为p/pm，p为各测点荷载值；位移无量纲化为Δ/Δm，Δ为各测点位移值），再进行数值拟合，其中pm为结构极限荷载，Δm为对应的位移。通过3个主要特征点的连线把曲线简化为三折线，将钢管混凝土柱脚节点抗冲切结构受力模型简化为三折线受力模型。这3个主要特征点分别为构件屈服荷载点A、构件极限荷载点B和构件极限变形点C（承载力下降到极限荷载的85%），简化的结构受力模型曲线见图1。

图1　简化的结构受力模型曲线

图1中特征点坐标的确定方法：控制点A代表构件屈服点，由能量等值法确定其荷载、位移值；控制点B代表最大承载点，其坐标为（1，1）；控制点C代表失效点，由p/pm=0.85和BC段回归方程确定其失效时的位移。结构受力模型各线段回归方程见表2。

表2　结构受力模型各线段回归方程

3.2结构受力模型验证

简化的结构受力模型曲线通过3个关键点（屈服点、极限荷载点、失效点）被分为3段折线，它反映了构件在受力过程中出现的典型特征。关键点确定后可将荷载-位移曲线复原，用于结构非线性计算［5］。

根据表2中结构受力模型各线段回归方程可知，只要确定了pm及Δm，即可确定结构的荷载-位移简化曲线。

根据计算公式（4）即可确定pm，采用试验方法确定Δm。通过对试验结果进行分析，钢管上加强构件在梁底面的投影面积和加强构件设置的高度对构件抗冲切变形起主要作用，因此采用多元线性回归，得到Δm的计算公式为

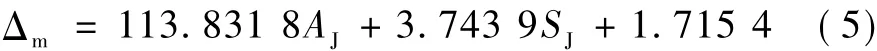
式中：AJ为钢管上加强构件外轮廓平面面积；SJ为加强构件距离梁底的高度与梁高的比值。

试件ZJ/J-6采用受力模型确定的计算曲线与试验曲线见图2。由图2可知，计算曲线与试验曲线趋势相同，吻合度较好。说明在竖向荷载作用下，钢管混凝土柱脚节点抗冲切结构受力模型能较好地描述构件的整个受力状态。

图2　ZJ/J-6计算曲线与试验曲线

4　结论

1）采用修正公式计算的抗冲切承载力理论值能与试验值相互验证。

2）拟合的结构受力模型确定的曲线与试件的试验曲线吻合较好，直接反映出了试件的受力破坏过程，可供此类钢管混凝土柱脚结构在竖向荷载作用下进行非线性反应分析与设计计算。

［1］王秀丽，刘明路，师伟.新型方钢管混凝土柱与混凝土梁的节点破坏机理［J］.兰州理工大学学报，2006，32（6）：131-135.

［2］卜永红，王毅红，张耀，等.钢管混凝土柱与钢筋混凝土基础节点抗冲切性能试验研究［J］.建筑结构，2013，43（7）：94-98.

［3］王毅红，胡静，薛源，等.带抗剪环的钢管混凝土柱脚节点受力性能的试验研究［J］.铁道建筑，2012（4）：23-26.

［4］蔡绍怀.现代钢管混凝土结构［M］.北京：人民交通出版社，2003.

［5］朱伯龙，张琨联.矩形及环形截面压弯构件恢复力特性的研究［J］.同济大学学报，1981，9（2）：1-10.

Calculation Analysis on Anti-punching-shear for Nodes of Concrete-filled Steel Tube Column and Reinforced Concrete Foundation Beam

BU Yonghong，WANG Yihong，YAN Weiheng，SUN Shanshan
（School of Construction Engineering，Chang'an University，Xi'an Shaanxi 710061，China）

Based on the test results of eight specimens under vertical load，which were nodes of concrete-filled steel tube（CFST）columns embedded in reinforced concrete（RC）foundation beams，the accurate anti-punching-shear calculating formula was given of the nodes by the method of theoretical analysis and data fitting.Based on the typical characteristics of specimens，the three-line mechanical model of the structure was fitted by numerical simulation，then compared with the experimental results.T he results show that the curves determined by the presented three-line mechanical are good agreement with the experimental curves of the specimens，which clearly indicate the failure process.T he presented model can be adopted to analyze nonlinear response and design calculation of the CFST column foot nodes under vertical load.

CFSTcolumn；Column foot node；Punching shear；M echanical model of the structure；Design calculation

TU375.3

ADOI：10.3969/j.issn.1003-1995.2016.09.13

1003-1995（2016）09-0051-03

（责任审编郑冰）

2016-03-08；

2016-05-26

中央高校基本科研业务费（2013G3284016，310828151069）；陕西省自然科学基金（2015JQ5134）

卜永红（1975—），男，高级工程师，博士。