基于不确定因素下的Floyd算法改进

基于不确定因素下的Floyd算法改进

在错综复杂的现实交通网络中，如何寻找一条可靠、安全、耗时短的最优路径是所有驾驶人员关心的问题。目前传统算法寻找最优路径，多数是以行车距离最短为目标，通过研究最短的路程来确定最优路径。在现实交通状况下，大多数驾驶员更希望找到一条行车时间最短的路径，然而行车时间会受到多种（不确定性）因素，如：红绿灯、交通拥堵、早中晚高峰期、道路自身状况、天气（雾霾、暴雨、地面结冰等）等因素的影响。因此在实际交通状况下，车辆的行驶时间长短存在着不确定性。

当今车载导航在寻找最优路径时，多数以最短路径为目标，虽然近些年不少人开始研究不确定因素对最优路径的影响，但仍旧没有具体的算法模型能运用到导航中，帮助驾驶员快速高效的寻找出行车时间最短的路径。本文提出改进的Floyd算法，为此类问题的解决提供了一个很好的思路。

Floyd算法

传统Floyd算法

1978年该算法由罗伯特.佛洛伊德命等人创立，主要用来寻找最优路径。算法步骤如下：

算法基本步骤：

（1）输入边矩阵D（0）=D。

以总路程最短来寻找最优路径，忽略不确定因素的影响，这样的状态为理想状态，求出的是距离最短的路径，并不一定是时间最短的路径。现对该算法进行如下改进。

改进Floyd算法

对于传统的算法，利用最短距离为目标来寻找最优路径，把路程作为路径优良的唯一衡量目标，但是实际生活中，人们一般追求的是行车路径可靠、安全、耗时短。所以，本文提出改进的Floyd算法，以行车时间最短为目标，考虑红绿灯、交通拥堵、天气变化等因素的影响，其基本思想如下。

（1）算法改进的基本思想

在理想交通状况下，设第i n 段路程的行车时间为t tn；实际交通状况下，由第m 种因素造成的第i n段路程延迟时间设为从而得到各路段的行车时间。将传统Floyd算法中，从而得到新定义的以时间为边权的矩阵A，按照传统Floyd算法的步骤，计算得出行驶最短时间的最优路径。

（2）改进算法步骤

step1：利用每两个节点间的理想行驶时间加上每段路的延迟时间，计算得到每两个节点间的实际行驶时间ti。

step2： 从任意一条单边路径开始，各节点之间的行驶时间表示为时间边权值，如果从节点i 到j 有路可达，则T［i，j］=t，t表示两节点间的实际行车时间，如果两点之间无边直接连接，则其边权值为无穷大，即T［i，j］=∞。以此类推，将图用邻接矩阵T 表示。

step3： 定义一个矩阵Path ，用于记录所插入点的信息，Path［i，j ］表示从节点i 到j 需要经过的点，初始化Path［ i，j］=0。对于每一对节点i 和j ，寻找是否存在一个节点k 使得从i→k→j 比已知时间更短。如果存在，即T［i，j］＞T［i，k］+T［k，j］，则T［i，j］=T［i，k ］+T［k，j］，同时将k 点信息记入矩阵Path［i，j ］；如果不存在，则继续遍历下一个节点。以此类推，当遍历完所有节点时，输出矩阵T，Path 。矩阵T包含了各节点间的最短行车时间的数据，矩阵Path包含了到达各节点所经过的路径数据。

算法用流程图如图1所示。

不确定因子的量化

根据调查，自贡市行车时间主要受红绿灯、路面状况、车辆数目的影响，因为车辆数目和路况对行车的影响主要是通过拥堵来表现，因此本文针对红绿灯与道路拥堵情况进行以下研究。

红绿灯

红绿灯是行车时间延误的重要影响因素，当下有很多方法试图解决信号交叉口时间延误问题，比如，流体力学法、排队论法、协调变换法等，但是均不能很好的解决实际问题。

因此，本文采用统计学方法，确定红绿灯造成的时间延误为该段路程理想行车时间的25%～33%。考虑到不同地区红绿灯时长设置不一样，同一地区不同地段红绿灯设置也不一样，因此对红灯时长在70s及其以上的地方，设置其造成的时间延误为该段路程理想行车时间的33%，60s～70s设置为30%，60s及其以下为26%。

图2　自贡市汽车站到彩灯公园交通网络图

拥堵影响

在实际交通网络中，不同时间段的拥堵情况不同，因此对行车造成的延误也不同，根据时间将拥堵划分为高峰期和非高峰期两类。

高峰期

早中晚高峰期对车速有一定影响，参考当地以往早中晚高峰期交通数据，由于拥堵对车速造成的影响，根据调查研究，对每段路在高峰期和平常的拥堵情况作了一个调查，根据调查数据将每段路的拥堵程度进行定量分析，（通畅、拥堵、较拥堵、很拥堵四个级别，分别代表行使速度在40km/h以上、40～30km/h、30～10km/h、5km/h以下），每段路所引起的时间延误

其中，si为第i 条路长；

v 为理想行驶速度；

vi为实际该段路的行驶速度。

由于车速受早中晚高峰期影响，造成行车时间延长。根据惩罚函数，设定路段拥堵程度的判断标准，其标准如下。

参照当地早中晚时期车速、车辆数目等数据，对其拥堵情况按上述标准进行判断。每段路所引起的延误时间：

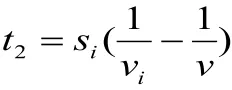
非高峰期

由于路况较差或者该地区过于繁华及其他原因，会造成某些路段即使在非高峰期时也比较拥堵，这些路段造成的行车时间延误在实际交通网络中不可忽略，为保持变量的统一性，非高峰期拥堵因子量化同早中晚高峰期。

案例分析

本文以自贡市汽车站到彩灯公园为例，截取其交通网络图如图2所示。

采用上述研究方法将不同路段红绿灯及拥堵造成的时间延误量化如下（以s计）。

表1　各路段不确定因素量化结果

采用传统Floyd算法可得到如下最短距离路径：

0→1→2→5→4→11

将传统Floyd算法得出的路径加入不确定因子，分别对红绿灯和拥堵情况进行量化，得到延误时间，根据定义，实际行车时间为理想行车时间与延迟时间之和，计算得到传统Floyd算法的实际行驶时间为1189s。

改进后的Floyd算法得出的最优路径结果如下：

A.高峰期：0→1→6→7→8→9→10→11

B.非高峰期：0→1→2→5→4→11

采用改进后的算法所得总时间为716.9s。

可以看出，在非高峰期，传统算法和改进后算法所得搜寻结果一致，而在高峰期二者差异较大，现对高峰期二者搜寻路径的行车时间进行比较。

表2　传统算法和改进算法结果对比

从上表可以看出，传统算法只在搜索最短路径具有较大优势，加入不确定因子的影响以后，本文所改进的算法搜寻出的路径结果明显优于传统算法。

总结

本文考虑的不确定性因素为红绿灯影响、早中晚高峰期及非高峰期拥堵因素影响，在生活中不可忽略的还有季节因子影响（雾霾、暴雨、地面结冰等）等因素，在真正的车辆导航系统中必须将当地所有因素考虑全面，因此在将来的研究中会重点对这些不确定性因素进行考察，将其量化，模拟出更真实的交通网络影响因子。

10.3969/j.issn.1001- 8972.2016.18.017