多变量控制算法在重大装备中的应用研究

沈玉玲，韩滨旭，谢　君

（上海电气集团股份有限公司中央研究院，上海 200070）

多变量控制算法在重大装备中的应用研究

沈玉玲，韩滨旭，谢君

（上海电气集团股份有限公司中央研究院，上海 200070）

提出了基于伴随矩阵的多变量解耦控制方法，不仅对耦合回路实现了完全解耦，而且独立设计的分散控制器也得到了满意的控制效果。最后，将此方法在球磨机装备中进行了仿真应用，结果也表明该方法是一种有效且简单易行的控制方法。

多变量系统；解耦控制；PI/PID控制器；重大装备

0　引言

多变量控制技术作为一种先进的控制手段，在大型复杂工业过程控制领域已取得了成功应用，尤其对于一些耦合严重的多变量过程系统。多变量控制技术在重大装备中的应用，首先要解决的一个难题，就是模型未知或不确定性，而大多数的多变量控制策略都是基于准确的控制对象模型提出的，这对于控制系统的鲁棒性能是严峻的考验。

多变量解耦控制技术从Morgan在1964年发展至今，从传统解耦控制、自适应解耦、鲁棒解耦到智能解耦等各种解耦方法，目前多变量解耦控制的应用研究已成为当前控制理论领域和工业装备领域共同关注的热点，设计简单且易行有效的控制方法，是今后的研究方向［1］。

本文提出了一种基于伴随矩阵的多变量解耦控制算法，可轻松的解决两输入两输出多变量系统的控制问题，仿真结果也表明，该方法在重大装备系统的应用也是完全可行的。

1　多变量控制技术

一个典型的多变量解耦控制系统结构框图如图1所示，其中G（s）为多变量系统；GI（s）为解耦器；GC（s）为分散控制器，解耦后的多变量系统表示为：

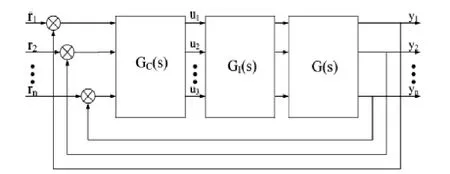
图1　多变量解耦控制系统

在理想解耦控制下，GR（s）为一个满足稳定性、正则性和因果性的传递函数矩阵。

为了将强耦合性的多变量系统解耦成多个独立的单变量系统，解耦器GI（s）有多种设计方案。理论上，多变量系统的逆过程G-1（s）可以作为解耦器的一种设计之一，由于：

事实上，许多静态和动态解耦控制方法均是由此衍生出来［2，3］。然而G-1（s）本身结构复杂且不利于实际应用，最糟糕的是它是物理不可实现的。因此，解耦器GI（s）可以进一步修正为：

其中GD（s）为选定的目标对角阵，满足GI（s）为物理可实现的。解耦后的多变量系统为：

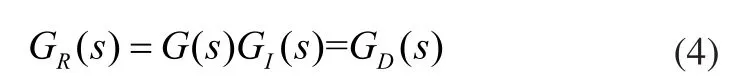
最后，利用文献中经典的单变量控制器设计方法，控制器GC（s）为GR（s）设计即可得出。

2　解耦器设计

由式（3）可知，一种简单可行的基于逆阵的解耦器设计为：

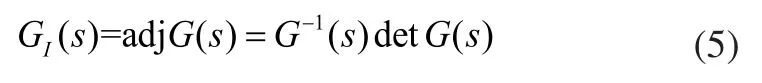
其中adjG（s）表示为G（s）的伴随矩阵，且它是物理可实现的。尤其是对于两输入两输出的多变量系统而言，G（s）的伴随矩阵无需计算即可直接写出。当adjG（s）作为解耦器作用在原多变量系统后，G（s）被完全解耦为对角阵，即：

因此，adjG（s）作为解耦器是完全可行的。

为了加快闭环系统的响应速度，解耦器被修正为：

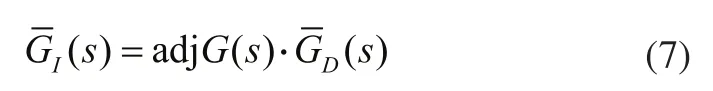
其中：

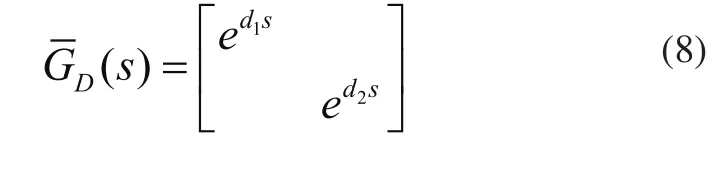
相应地，解耦后的多变量过程修正为：

3　分散控制器设计

不失一般性，多变量系统行列式矩阵表示为二阶加纯滞后（SOPDT）的形式，即：

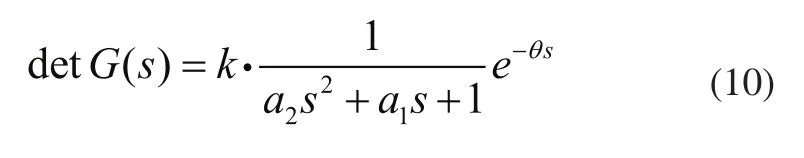
其中模型参数有脉冲响应辨识得到［4］。 将式（8）和式（10）带入式（9）中得到：

多变量分散控制器GC（s）为设计得到，并可表示为：

其中gc，ii为独立设计的PID控制器，现有的单变量控制器设计方法均可采用，满足其稳定性的要求，得到满意的控制效果。本文中gc，ii采用标准的PID控制器形式，即：

控制器设计方法采用经典的GPM方法［5］。

4　在火电厂磨煤机中的仿真应用

火电厂中球磨机具有多变量、强耦合、大时滞等特点，建立精确的数学模型比较困难。典型的球磨机可以看做一个3×3的多变量系统，并可进一步分解成一个2×2多变量系统和一个单变量系统的组合。本文仅研究2×2多变量系统的控制问题，即控制量为热风量R和循环风量W，被控输出为温度T和负压P，两个回路之间有很强的耦合性，被控对象可描述为：

在两种不同工况下，对某球磨机进行辨识，得到其数学模型分别为［6］：

采用本文方法，设计得到的解耦器和控制器分别为：

图2　工况一下的闭环控制系统仿真曲线

在第一种工况下的仿真结果如图2所示，表明本文方法能达到满意的解耦控制效果，同时控制曲线平滑。在控制器保持不变的情况，切换至第二个工况，控制效果如图3所示，同样也得到了满意的解耦控制效果，表明控制系统具有很强的鲁棒性和抗干扰性。

5　结论

许多重大装备都可描述为多变量系统，多变量控制算法可以考虑在重大装备控制中进行应用。本文提供了一种基于伴随矩阵的多变量解耦算法，并在火电厂磨煤机中进行了仿真应用，在解耦和输出跟踪方面都收到了满意的效果。

图3　工况二下的闭环控制系统仿真曲线

［1］ 马平，杨金芳，崔长春，胡胜坤.解耦控制的现状及发展［J］.控制工程，2005，12（2）:97-98.

［2］ Lee， J.； Kim， D. H.； Edgar， T. F.Static decouplers for control of multivariable processes. AIChE J.2005，51，2712-2720.

［3］ Pomerleau， D.；Pomerleau，A.Guide lines for the tuning and the evaluation of decentralized and decoupling controllers for processes with recirculation. ISA Trans.2001，40，341-351.

［4］ 孟庆波，葛惠民.基于单位脉冲响应的二阶加纯延时系统辨识［J］.机械制造，2012，50（570）:25-26.

［5］ 张永华，姚明海.基于GPM法的PID参数模糊自整定方法［J］.自动化与仪器仪表，2002（6）:4-6.

［6］ 程启明，郭瑞青，杜许峰，郑勇.无模型多变量解耦控制方法及其在球磨机控制中的仿真应用［J］.动力工程，2008，28（6）:891-895.

Application of multivariable control scheme in major equipments

SHEN Yu-ling，HAN Bin-xu，XIE Jun

TP273

A

1009-0134（2016）09-0014-03

2016-06-01

上海市科委优秀技术带头人计划（14XD1420900）；上海市科委企业合作专项项目（15dz1180400）

沈玉玲（1980 -），女，山东德州人，工程师，博士，主要从事工业过程控制相关领域的研究工作。