基于高维数据的改进CCC-GARCH模型的估计及应用

刘丽萍，马　丹，唐晓彬

(1.贵州财经大学 数学与统计学院，贵州 贵阳 550025；2.西南财经大学 统计学院，四川 成都 611130；3.对外经济贸易大学 统计学院，北京 100029)



【统计理论与方法】

基于高维数据的改进CCC-GARCH模型的估计及应用

刘丽萍1，马丹2，唐晓彬3

(1.贵州财经大学 数学与统计学院，贵州 贵阳 550025；2.西南财经大学 统计学院，四川 成都 611130；3.对外经济贸易大学 统计学院，北京 100029)

高维数据给传统的协方差阵估计方法带来了巨大的挑战，数据维度和噪声的影响使传统的CCC-GARCH模型估计起来较为困难。将主成分和门限方法有效结合，应用到CCC-GARCH模型的估计中，提出基于主成分正交补门限方法的CCC-GARCH模型(PTCCC-GARCH)。PTCCC模型主要通过前K个最优主成分来刻画大维协方差阵的信息，并通过门限函数以剔除噪声的影响。通过模拟和实证研究发现：较CCC-GARCH模型而言，PTCCC-GARCH模型明显提高了高维协方差阵的估计和预测效率；并且将其应用在投资组合时，投资者获得了更高的投资收益和经济福利。

主成分正交补门限方法；主成分正交补门限CCC-GARCH模型；高维协方差阵

一、引 言

21世纪是信息爆炸的时代，计算机技术的飞速发展极大地方便了数据的获取和存储，许多科学研究领域产生了多种多样的复杂超高维海量大数据。近年来，对于高维数据的研究主要集中在变量选择方面[1-2]，而在金融领域中(超)高维金融资产组合的构建对于很多个体和金融机构来说非常常见。当资产维度较高、数据量很大时，协方差阵的估计将面临着维数诅咒、噪声影响等诸多挑战，传统的协方差阵估计和预测模型不再适用。如何估计金融大数据的协方差阵已引起了学者们的广泛关注，国内外研究成果主要包括四类：第一，基于主成分分析和因子分析的高维协方差阵估计方法。J.Fan和Y.Fan等以及J.Fan和Liao等提出了基于因子结构的协方差阵估计方法[3-4]，J.Fan和Y.Liao等将主成分分析法应用到高维协方差阵的估计中[5]，该类方法在假定因子数目或主成分数目已知的情况下，通过提取公共因子或主成分来解决维数诅咒问题和降低噪声的影响；第二，基于门限稀疏法的高维协方差阵估计方法。Lam和Fan、Cai和Zhou、Cai和Liu等人提出的稀疏协方差阵估计方法在假定矩阵很多元素为0的基础上，通过引入门限函数来解决维数诅咒问题，有效降低了资产的维度[6-8]，但有研究指出：由于公共因子(市场风险)的存在，假定多个资产不相关(元素为0)实际上并不太合理；第三，基于收缩法的高维协方差阵估计方法。Ledoit和Wolf将样本协方差阵和单因子协方差阵进行加权平均，采用收缩法来估计高维数据的协方差阵[9]，该方法并没有得到广泛应用，因其估计效果与最优权重的选择密切相关，而最优权重不易确定；第四，基于非参或半参数统计方法的高维协方差阵估计方法。Dai和Guo以及Li和Wang等人采用非参数估计方法估计了高维数据的协方差阵[10-11]，该方法将乔列斯基分解法和非参数收缩法(常采用惩罚函数进行系数压缩)相结合，有效解决维数诅咒问题并保证了协方差阵估计的正定性。值得注意的是，该类方法的估计效果与惩罚函数的选择密切相关。

CCC-GARCH模型是由Bollerslev提出的常条件相关性模型[12]，该模型是常见的用以估计和预测金融资产协方差阵的多元GARCH模型。但是，当考虑的资产维度较高、数据量较大时，CCC-GARCH模型将不再适用，为此本文对高维数据协方差阵的估计进行探讨。对于大规模高维度的协方差阵的估计，笔者不再简单地采用CCC-GARCH模型，而是在前人研究的基础之上对CCC-GARCH模型进行改进，将主成分和门限方法应用在CCC-GARCH模型的估计中，提出新的估计量——主成分正交补门限CCC-GARCH(PTCCC-GARCH)模型。

PTCCC-GARCH模型的估计并不复杂，主要是将矩阵的谱分解方法应用到CCC-GARCH的相关性矩阵的估计中，以提取其主要信息而达到降维的目的；然后将门限函数应用到矩阵的正交补中，以剔除噪声的影响。

二、主成分正交补门限CCC-GARCH(PTCCC-GARCH)模型的提出

(一)CCC-GARCH模型的回顾

Bollerslev提出的CCC-GARCH模型是比较经典的多元GARCH模型，是最常用的协方差阵预测模型。根据Bollerslev的研究, 设k个资产的回报率向量为rt，并假定其服从多元正态分布：

rt|Φt-1～N(0,Ht)

(1)

Ht≡DtRDt

(2)

其中Ht是k个资产的常条件协方差矩阵; R是k×k阶的常系数相关矩阵，

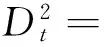
(3)

(4)

可见，CCC-GARCH模型的估计主要分为两步：第一步是式(3)估计得到单个资产的条件方差Dt；第二步是式(4)估计多维资产的相关性矩阵R，进而根据式(2)得到其动态协方差阵Ht。对于CCC-GARCH模型，单个资产的条件方差是采用一元的GARCH模型来估计的，估计起来较为简单；但是对于相关性矩阵R，当考虑的资产维度较高、数据量较大时，其估计就变得较为困难。

(二)PTCCC-GARCH模型的提出

(5)

(6)

其中τij表示门限函数，sij(·)表示收缩函[13]，当Σu的元素uij≥τij时，便需要依赖sij(·)对其调整。

(7)主成分正交补门限CCC-GARCH(PTCCC-GARCH)模型的具体表达式如下：

(8)

(9)

可见，PTCCC-GARCH模型主要是通过提取少数几个主成分来揭示高维资产间的关系，达到降维的目的；通过引入门限函数来剔除噪声的影响，使得高维协方差阵的估计得以实现。

三、模拟研究

(一)模拟数据的产生

PTCCC-GARCH模型虽能解决维数诅咒问题，但其估计效率是否优于CCC-GARCH模型值得研究。首先采用模拟研究对其进行比较，为了使其比较更具说服力，本文根据CCC-GARCH模型产生收益率数据，数据的产生步骤如下：

1.模拟单变量的GARCH模型，计算出单个资产的条件方差。假定w∈[0.000 5, 0.005]、k∈[0.01, 0.1]、λ∈ [0.5, 0.88],在w、k、λ的取值区间内分别随机产生p个值，然后根据式(3)的GARCH模型，可以得到单个资产的条件方差Dt。

2.随机产生一个正定的p×p的无条件相关性矩阵R。

3.计算出协方差阵Ht，Ht=DtRDt，最终产生服从CCC-GARCH模型的收益率数据rt，rt|Φt-1～N(0,DtRDt)。

4.重复1～3步N次，便得到了N次的模拟数据，在本文的模拟研究中N=100。本文分别模拟了维度为p=100,150,200的资产，并且样本区间为T=400、600、800、1 000。

(二)主成分及门限函数的选择

1.主成分K的选择。在估计PTCCC-GARCH模型时，首先面临的问题是最优主成分数目K的选择。对于K的选择，本文采用均方误差MSE作为评价标准，损失函数MSE有效地衡量了PTCCC-GARCH估计的动态协方差阵与基于模拟数据的真实协方差阵的差异，差异越小表示PTCCC-GARCH模型的估计效果越好，所以最优的主成分个数K应该使MSE的值最小。

本文采用数值搜索法来选择最优主成分：首先设定K的取值范围为1～10，然后在设定的取值范围内进行不断搜索来寻找最优主成分个数K；当K取不同值时，与之相对应的PTCCC-GARCH估计值也不同。图1给出了不同资产维度、不同样本容量下，最优主成分数目的选择。

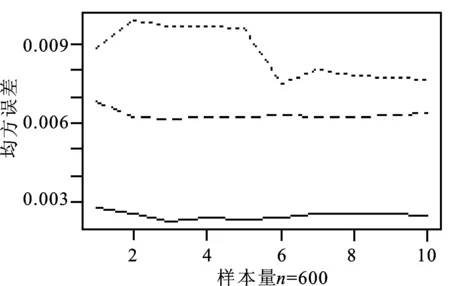
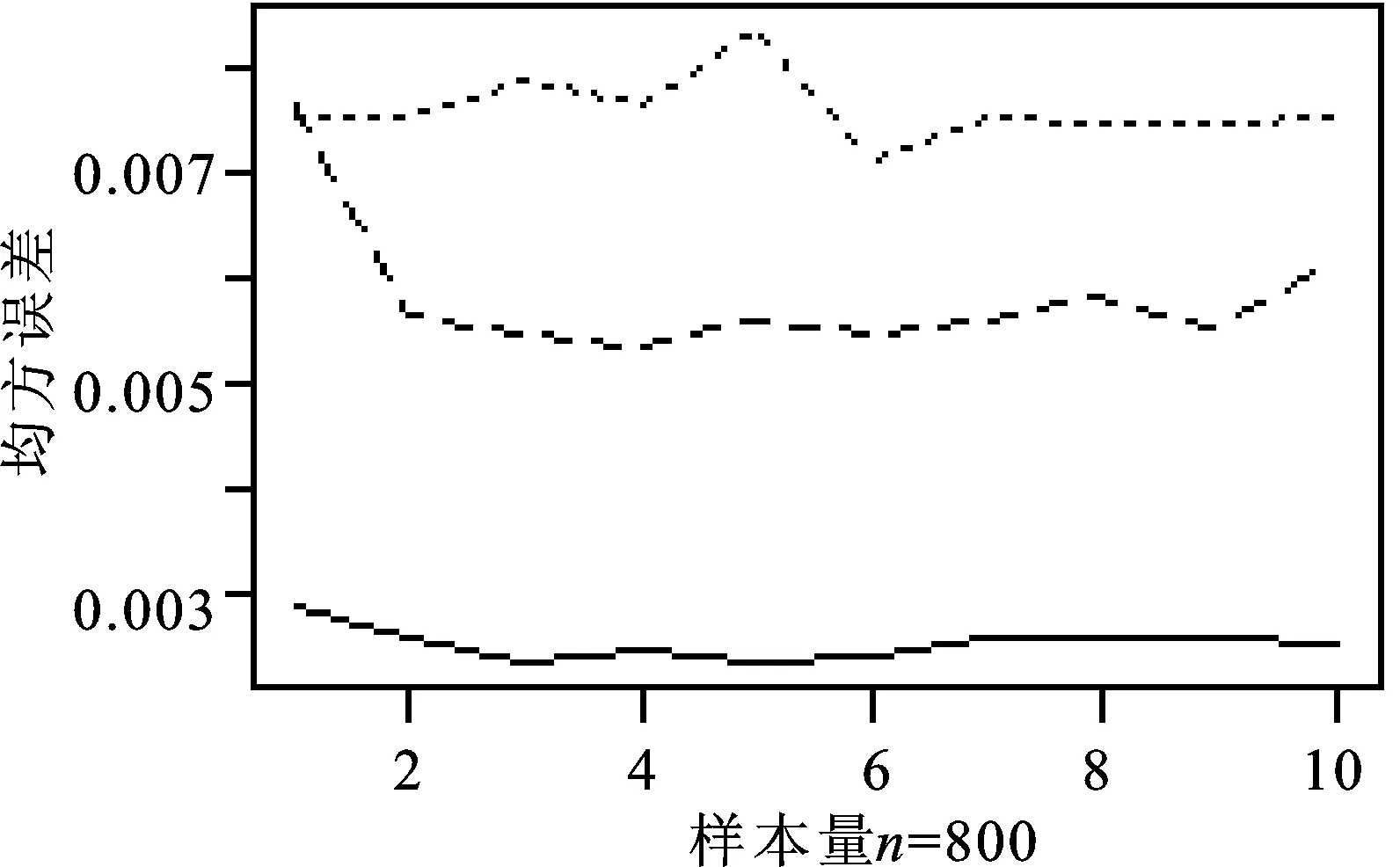
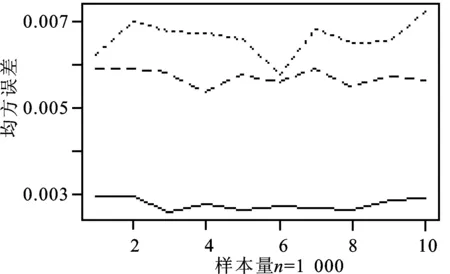
图1　最优主成分数目选择图(…p=200,---p=150,—p=100)

从图1不难发现：K的选择与资产维度p息息相关，与样本量n的大小几乎无关。当资产的维度p=100时，最优的主成分个数为3，此时PTCCC-GARCH估计的协方差阵与真实的协方差阵的平均MSE最小；当p=150和200时，其对应的最优主成分的个数分别为4和6，可见随着考虑的资产维度的增加，其对应的最优主成分个数K也随之增加。

2.门限函数的选择。高维数据中噪声的影响不容忽视，为剔除其影响提高协方差阵的估计效率。由式(6)知在估计协方差阵Σu时需加入门限函数，本文采用的是Cai和Liu提出的门限函数，其形式为：

(10)

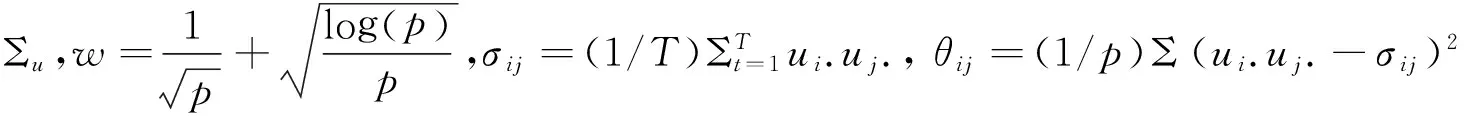
(11)

其中u为矩阵Σu的元素；I为示性函数，当|uij|≥τij时，I取1，否则为0；sij(·)是Antoniadis和Fan提出的广义收缩函数，|sij(uij)-uij|≤τij。本文选取了“柔性”收缩函数，其表达式为:

sij(uij)=Sgn(uij)(|uij-τij|)

(12)

(三)PTCCC-GARCH模型和CCC-GARCH模型的比较

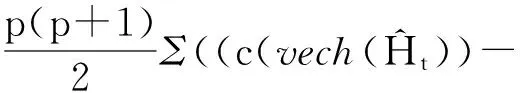
c(vech(Ht)))2)

(13)

(14)

其中REt表示估计矩阵的相对误差，损失函数越小表示估计的协方差阵与真实的协方差阵差异越小，其估计效果越好。为了能够更好地说明PTCCC-GARCH模型的估计效果，本文不仅给出了K取最优数目时所对应的损失函数的均值，还给出了K取1时，所对应的损失函数的情况。表1和表2分别给出了损失函数MSE、RE的均值：

表1　估计的协方差矩阵的均方误差均值比较表

表2　估计的协方差矩阵的相对误差均值比较表

根据表1和表2可以得出两条重要结论：其一，无论对于损失函数MSE还是RE，无论样本量和资产维度是多少， PTCCC-GARCH模型对应的损失函数的值要明显小于CCC-GARCH模型的损失函数值，并且随着数据维度的增高和样本量的增大，PTCCCC-GARCH模型的估计效果越好；第二，主成分数目K的选择直接影响到PTCCC-GARCH模型的估计效果，当K取到最优值时，PTCCC-GARCH模型对应的损失函数的均值最小，其估计效果最好。

四、实证研究

(一)样本数据处理

本文采用的数据来自于CSMAR数据库的上证180指数成分股。样本数据来自于2011年1月4日到2014年9月30日，剔除交易的缺失数据后样本区间的长度为906天。将整个样本区间划分为两部分，其中估计窗口的长度为706天，预测窗口的长度为200天。分别采用PTCCC-GARCH模型和CCC-GARCH模型来估计和预测180支股票的协方差阵时，采用的是滚动时间窗法，即第一次估计时估计区间为t=1,2,…,706，用该样本来估计CCC-GARCH和PTCCC-GARCH模型，据此预测第707天的协方差阵，并根据预测的协方差阵构造第707天的投资组合；保持估计区间的长度仍然为706天，将估计区间向后推1天，从而可得第二次的估计区间为t=2,3,…,707，此时重新估计CCC-GARCH和PTCCC-GARCH模型，并预测第708天的协方差阵，根据预测的协方差阵构造第708天的投资组合；如此重复，直到估计区间的长度为t=200,201,…,905，重新估计模型，预测第906天的协方差阵，进而可以构造出第906天的投资组合。

(二)预测的协方差阵在投资组合中的应用

为了研究PTCCC-GARCH模型的应用情况，本文将其应用于投资组合中，从组合效率的角度展开，以De Pooter等人[14]采用的两条评价标准来分析其组合效率：一是从夏普比率的角度展开，夏普比率是反映组合风险与收益关系的重要指标；二是从效用函数的角度展开，效用函数可以有效衡量不同投资组合的经济福利。

1.各投资组合的收益和波动分析。本文主要采用最小方差和等比例风险投资组合。等比例风险投资组合是近年来才被提出的，该组合通过不断调整权数，使投资组合中每个资产所承担的风险比例相同。当资本市场不存在卖空现象时，等比例风险投资组合的权数满足下式：

(15)

利用CCC-GARCH模型和PTCCC-GARCH模型，采用滚动预测法分别预测出200天的协方差阵后，就可将预测每天的协方差阵带入到投资组合模型中，继而计算出该天的组合收益和波动。表3列出了两种投资组合的平均收益、组合波动以及Sharpe比率。

表3　不同投资组合的平均收益、组合波动和夏普比率表

从表3不难发现：无论选择最小方差投资组合还是等比例风险投资组合，较CCC-GARCH模型而言，根据PTCCC-GARCH模型所构造的投资组合的平均收益较高，波动较小，并且所对应的sharpe比率明显要高于CCC-GARCH模型。可见，PTCCC-GARCH模型的预测效果明显要优于CCC-GARCH模型，这是因为将主成分正交补门限方法应用到了模型的估计中，从而解决了维数诅咒问题，并剔除了噪声的影响。

2.各投资组合的经济福利分析。效用函数是常用的经济福利分析函数，在一定风险偏好下投资者对投资的评价通常是通过二次效用函数来反映的。假定W0为投资者的初始财富，则反映投资者经济福利情况的二次效用函数的形式为：

(16)

(17)

(18)

(19)

表4　最小方差投资组合的年化效用函数表

表5　等比例额风险投资组合的年化效用函数表

从表4表5不难发现：无论对于最小方差投资组合还是对等比例风险投资组合，在投资风险偏好相同的情况下，较CCC-GARCH模型而言，由PTCCC-GARCH模型所构造的投资组合的总效应函数和净效应函数明显更高，说明在高维数据背景下采用PTCCC-GARCH模型估计和预测协方差阵，有助于提高投资者所获得的经济效用。除此之外，投资者所获得净效应函数较总效应函数要低，进一步说明交易成本对效应函数的影响不可忽略。

五、结　论

高维数据背景下，传统的协方差阵估计和预测模型不再适用，如何有效地估计和预测高维数据的协方差阵已引起了学术界的广泛关注。本文将主成分和门限方法应用到CCC-GARCH模型的估计中，对其进行改进，提出了PTCCC-GARCH模型。该模型有效降低了数据的维度，在解决维数诅咒的同时还降低了噪声的影响，使高维协方差阵的估计和预测效率得到了明显的提高。

PTCCC-GARCH首先通过选择前K个最优主成分来刻画高维数据协方差阵的信息，有效降低数据的维度；然后将门限函数应用在主成分的正交补中，以剔除噪声的影响。根据本文的模拟研究发现：PTCCC-GARCH模型的估计和预测效果与主成分K的选择密不可分，当K取到最优的数目时，PTCCC-GARCH模型便具有最优的表现，即便K取1，PTCCC-GARCH模型的估计效率都要明显高于CCC-GARCH模型；通过实证研究发现：由PTCCC-GARCH模型所构造的投资组合明显优于CCC-GARCH模型，所获得的组合收益和经济福利更高。总之， PTCCC-GARCH模型提高了高维协方差阵的估计和预测效率，克服了CCC-GARCH模型的不足。

[1]马学俊.GSIS超高维变量选择[J].统计与信息论坛，2015(8).

[2]张景肖，李向杰，郭海明.HD-SIS超高维数据稳健变量筛选[J].统计与信息论坛，2016(4).

[3]Fan J, Fan Y, Lv J. High Dimensional Covariance Matrix Estimation Using a Factor Model[J].Journal of Econometrics, 2008(1).

[4]Fan J, Liao Y, Mincheva M. High Dimensional Covariance Matrix Estimation in Approximate Factor Models [J].The Annals of Statistics, 2011(6).

[5]Fan J, Liao Y, Mincheva M. Large Covariance Estimation by Thresholding Principal Orthogonal Complements [J].Journal of the Royal Statistical Society,2013(4).

[6]Lam C, Fan J.Sparsistency and Rates of Convergence in Large Covariance Matrix Estimation [J].Journal of Statist, 2009(6).

[7]Cai T, Zhou H. Optimal Rates of Convergence for Sparse Covariance Matrix Estimation [J]. The Annals of Statistics, 2012(5).

[8]Cai T, Liu W. Adaptive Thresholding for Sparse Covariance Matrix Estimation [J].Journal of the American Statistical Association, 2011(106).

[9]Ledoit O, Wolf M. Improved Estimation of the Covariance Matrix of Stock Returns with an Application to Portfolio Selection [J]. Journal of Empirical Finance, 2003(5).

[10]Dai M, Guo W. Multivariate Spectral Analysis Using Cholesky Decomposition [J].Journal of Biometrika, 2004(3).

[11]Li Y, Wang N, Hong M, et al.Nonparametric Estimation of Correlation Functions in Longitudinal and Spatial Data, with Application to Colon Carcinogenesis Experiments [J].The Annals of Statistics,2007(4).

[12]Bollerslev T. Modelling the Coherence in Short-run Nominal Exchange Rates: A Multivariate Generalized ARCH Model[J]. The Review of Economics And Statistics,1990(3).

[13]Antoniadis A， Fan J. Regularization of Wavelet Approximations [J].Journal of American Statistical Association, 2001(96).

[14]De Pooter M, Martens M P, Van Dijk D J. Predicting the Daily Covariance Matrix for S&P 100 Stocks Using Intraday Data-but Which Frequency to Use [J]. Journal of Econometric Reviews,2008(3).

[15]Maillard S, Roncalli T, Teiletche J. On the Properties of Equally Weighted Risk Contributions Portfolios [J]. Journal of Portfolio Management, 2010(4).

(责任编辑：郭诗梦)

Estimation and Application of the Improved CCC-GARCH Model of High Dimensional Data

LIU Li-ping1， MA Dan2， TANG Xiao-bin3

(1.School of Mathematics and Statistics, Guizhou University of Finance and Economics, Guiyang 550025, China；2. School of Statistics, Southwestern University of Finance and Economics, Chengdu 611130, China；3 .School of Statistics, University of International Business and Economics, Beijing 100029, China)

High dimensional data poses great challenges to the traditional estimation of covariance, it is difficult to estimate the traditional CCC-GARCH model because of the influence of data dimension and noise. We combine the principal components and thresholding method effectively and applies them to the estimation of CCC-GARCH model. The PTCCC-GARCH model is then proposed which is based on the principalorthogonal complement thresholding method. It characterizes the information of large covariance mainly through the first K principal components, the thresholding function is then applied in the orthogonal complement of matrix, so as to reduce data dimensions and exclude the noise effects effectively. Through simulation and empirical studies, it is found that PTCCC-GARCH model significantly improves the efficiency of estimation and prediction of large matrix and investors obtain higher returns and economical welfare when the PTCCC-GARCH model is applied in portfolio.

the principal components and thresholding method;PTCCC-GARCH; high dimensional covariance

2016-03-18；修复日期：2016-06-06

贵州省教育厅2015年度普通本科高校自然科学研究项目《大维数据背景下金融协方差阵的估计及应用》(黔教合KY字[2015]423); 2015年全国统计科学研究项目《金融动态条件协方差阵的估计及其应用》(2015LY19)；2015年度北京市社会科学基金青年项目《大数据背景下北京市网络风险动态监测与控制机制研究》(15SHC030)；2015年度全国统计科学研究重大项目《大数据视角下我国主要宏观经济指标预判预测方法体系研究》(2015LD050)

刘丽萍，女，山东菏泽人，统计学博士，副教授，研究方向：金融数量分析；

O212.4∶F224.0

A

1007-3116(2016)09-0022-07

马丹，女，四川宜宾人，统计学博士，教授，研究方向：金融风险管理，资产定价；

唐晓彬，男，安徽霍山人，统计学博士，讲师，研究方向：经济统计研究。