一种非同步采样下的微机测控装置直流滤波方法

王霄翔 程 立 熊慕文

（南京南瑞继保电气有限公司，南京 211102）



一种非同步采样下的微机测控装置直流滤波方法

王霄翔 程 立 熊慕文

（南京南瑞继保电气有限公司，南京 211102）

直流分量是影响测量精度的重要因素。使用均方根算法计算有效值时，为了在非同步采样下滤除直流分量，提出一种在非同步采样下的滤除直流分量的方法。该方法利用梯形积分原理，在系统频率和采样频率偏离的情况下，将一个周期内的采样点分为整数点和分数点，分别计算整数点和分数点的面积来计算直流分量。为求取分数点时对应的采样值，采用了线性插值算法。所提出的算法无需硬件频率跟踪电路，数据窗长度仅为一个周波，适合多种微机保护测控装置。实际装置运行表明，在系统频率在45～55Hz之间变化时，此方法可以有效滤除直流分量，提高装置测量精度。

均方根；非同步采样；直流分量；线性插值

大多数微机保护算法的计算就是对采样信号进行频谱分析而获得其参数估算的过程，对算法性能的评价也取决于是否能在较短的数据窗中获得精确的估计值。在各种算法中，傅里叶变换是被广泛使用进行信号频谱分析的重要工具。目前在微机继电保护测控算法中，比较经常使用的是离散傅里叶变换[1]。然而实际采样信号中，往往还包含着一些直流分量，必须要将直流分量可靠的滤除才能得到精确的测量结果。对于完整周期信号，离散傅里叶变换可以较为容易的滤除直流分量，人们进行了广泛的研究，如文献[2]基于三角函数的和差公式及线性方程组的求解，提出了一种新的递推离散傅里叶变换算法。在微机测量装置的实现过程中，如果只需要计算有效值不需要计算谐波分量，离散傅里叶变换算法的计量量较大，实现较为复杂；使用均方根（RMS）算法较为简单易行，但均方根算法受直流分量影响较大，需要使用可靠的方法滤除直流分量。测量装置采样通道较多，每一路通道的频率不一定一致，而装置采样频率只能保证和某一通道一致，这样采样频率和通道频率就不完全同步，这时实际采样就是为非同步采样[3]。同步采样时可以很容易的滤除直流分量，但非同步采样时，直流分量需要单独处理。

本文提出一种在非同步采样情况下滤除直流的算法，主要用于微机测控装置滤除稳态下的恒定直流分量。该算法基于的梯形积分原理，将系统频率偏移时，一个周期内的采样点数分为整数点和分数点两部分，并利用分数点的计算结果对整数点的计算结果进行修正。该算法仅需软件测频，无需修改硬件电路；算法简单直观，仅需一个工频周期的采样数据，计算量小、延迟短。实际装置运行表明，在系统频率发生变化时，依靠本算法依然能很好的滤除直流分量。

1　算法分析

1.1全波傅氏算法

全波傅氏算法可以滤除恒定的直流分量和基波整数次谐波分量。

假定被采样的信号具有如下形式：

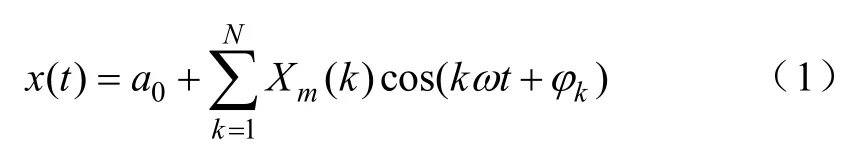
式中，a0为直流分量；分别为k次谐波的幅值和初相角。

根据傅氏级数原理，可以得到各次谐波分量的实部和虚部的时域表达式为

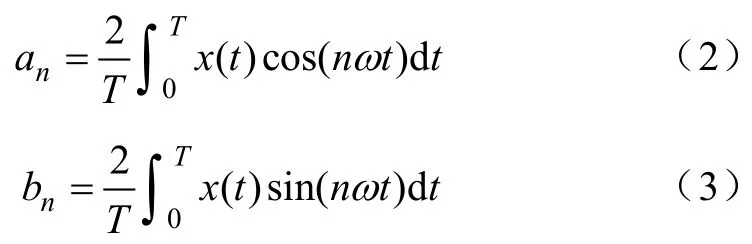
式中，T为基频分量的周期；ω为基频分量的角频率（ω=2π/T）。

将分解出来的实部和虚部时域表达式离散化处理后可得式中，k为采样点数序号；N为每周波采样点数。

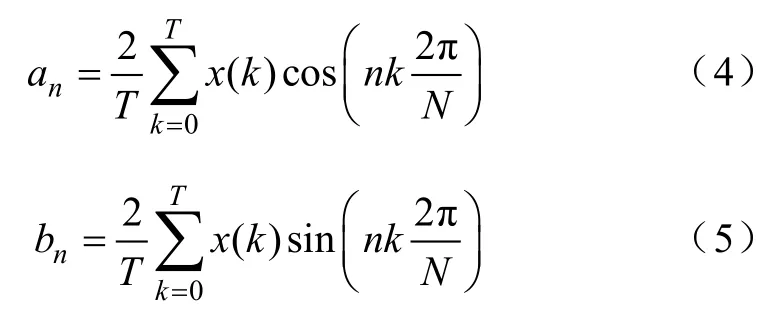
通过傅氏级数算法，可以得到直流分量、基波分量以及高次谐波分量。但是如果我们只需要基波分量时，傅氏级数算法虽然准确，但计算量大，实现起来比较复杂，会增加软件资源消耗。在这种情况下，一般不选用傅氏级数算法，选择较为简单的均方根（RMS）算法，可以很容易的得到有效值。

1.2均方根（RMS）算法

假定被采样的信号具有式（1）的形式若每周期采样点数为 N，可以使用均方根算法得到该信号的有效值，即

式中，x(i)为每个采样点的值。

从均方根算法的原理可以看出，在混入直流信号时，直流信号也会混入有效值之中，影响计算精度，故必须使用有效的方法滤除直流分量。

同步采样时，滤除直流分量的方法较多，可以将N个采样点的算数平均得到直流分量，但非同步采样时，所得到的采样点并不是一个完整周期，该方法已不再适用，需要使用其他方法。

1.3算法原理

设 x(i)是一个周期为 T的正弦连续信号，将连续信号离散化，每个周期的采样点为 N，可以很容易的得到曲线一个周期内的面积，即

对于一个不含直流分量的周期信号，正半周波和负半周波的面积相等，但符号相反，整个曲线所包围的面积S=0。

如果该周期信号包含直流信号，此时所求得的面积应为矩形ABCD的面积，如图1所示。该信号的直流分量应为

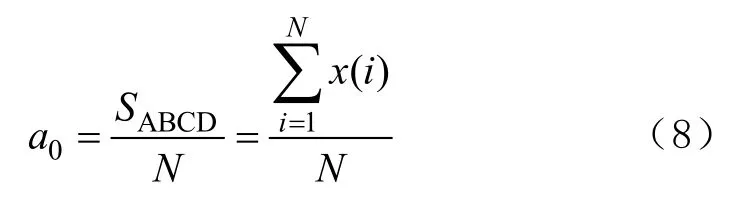
求得直流分量之后，可以对每个采样点进行直流滤波补偿，再进行其他计算，这样就消除了直流分量的影响。

当采样为非同步采样时，每个周期的采样点并不是N或者N的整数倍，这时直接采用式（7）计算面积时就会存在偏差，存在多加了一部分或者少了加了一部分面积的情况，不能得到准确的直流分量。

图1　周期信号

当系统采样频率 f 波动导致基波周期发生ΔT变化、而采样频率 fs固定不变时，一个周期内的采样点数为

对N取整得到整数采样点为

此时分数采样点为

例如，设采样频率 fs为 4kHz。当系统频率由50Hz偏移到49.6Hz时，可得Ns=80，N=0.65。

在非整周期采样下，将采样点N分为整数采样点Ns和分数采样点N，利用梯形积分算法分别计算其面积，然后用分数点面积补偿整数点面积，从而得到了完整的曲线面积，可以求得直流分量。

对于整数采样点 Ns，依然可以通过式（7）求得整数部分面积。

分数采样点N的面积计算如图2所示。图中曲线1位工频波形，曲线2位频率偏移时的波形。线段 ANsNsN和曲线 AN所包围的面积即为分数点面积。为计算此面积，需要首先获取N处采样点的值。我们已知Ns和Ns+1处采样点的值，通过线性插值可以求得N处采样点的值x(N)。

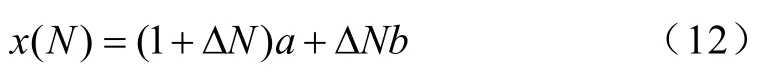
进而可求得分数采样点的面积，即

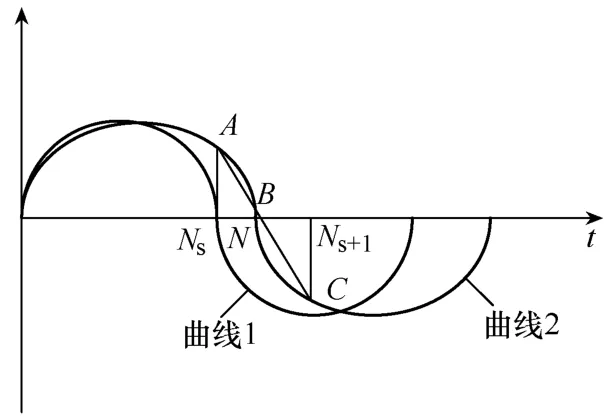
图2　面积补偿算法

利用整数采样点部分的面积Ns和分数部分的面积就可以得到此时的直流分量：

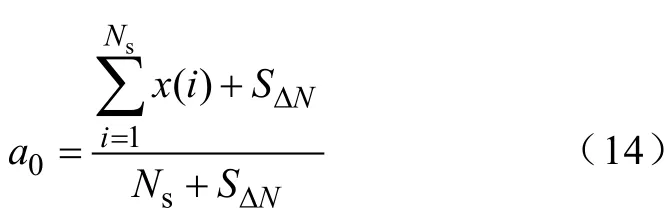
至此已经得到了直流分量，可以逐个采样点进行滤除直流的计算。

2　应用实现

在变电站中，交流电压电流经过二次PT/CT再经接入测控装置。测控装置内部经过A/D转换成数字信号，然后根据一定的采样周期进行采样，再对采样点进行滤波后进行保护测量计算。

测控装置一般有多个采样通道，比如单间隔线路测控装置会对母线侧电压和同期侧电压同时采样，需要对每个通道进行滤除直流后再进行计算，我们以母线侧的电压为基准进行频率跟踪，并以该频率为基准进行采样。在线路开关合上时，母线侧和线路侧电压处于同一个系统内，他们频率相同，故测控装置使用同一个采样周期对所有通道进行采样均是同步采样；当线路开关断开，需要进行同期合闸时，线路侧和母线侧的频率就会存在偏差，此时同期侧电压采样就是非同步采样。虽然线路侧和母线侧频率相差不大，但造成的计算误差会超过测控装置要求的0.2%精度范围，需要单独处理。流程图如图3所示。

测控装置改进前，仍然使用将N个采样点算数平均的方法计算直流分量进行直流滤波。在频率偏离采样频率时会出现较大误差，且采样值抖动，不能满足0.2%精度要求。测量结果见表1。

采用本文所述方法改进后，在频率偏离采样频率的情况下，装置计算有效值稳定，不再出现抖动或跳动的情况，能够满足0.2%的精度要求。测量结果见表2。

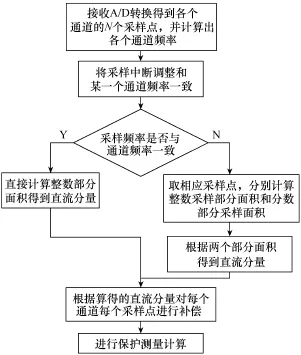
图3　流程图

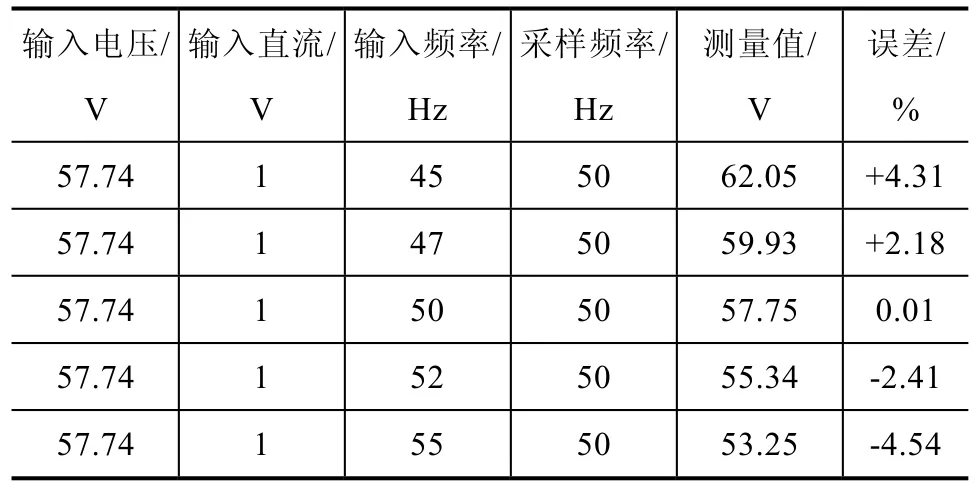
表1　改进前测量结果

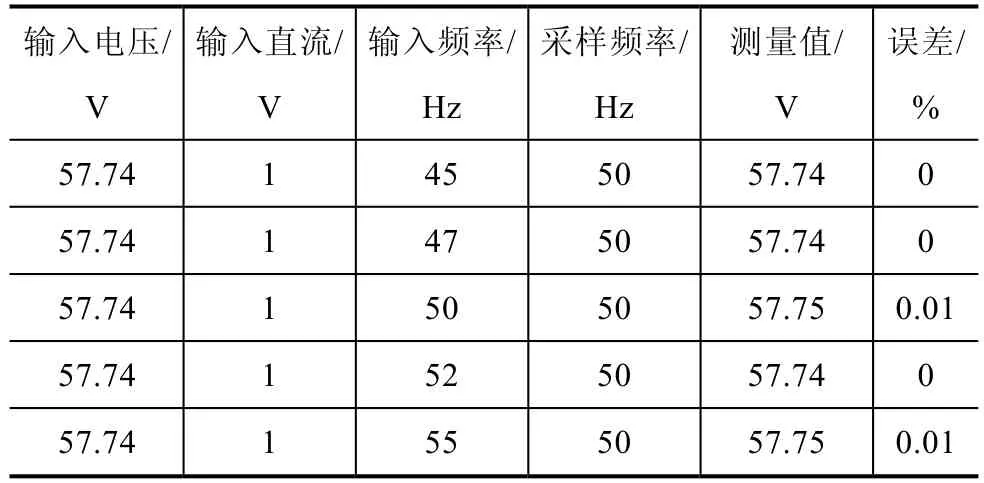
表2　改进后测量结果

3　结论

本文提出一种在非同步采样条件下，利用梯形积分修正方法的滤除直流算法。当系统频率和采样频率不一致时，利用线性插值计算分数采样点，利用分数采样点的面积和整数采样点的面积来进行直流分量的计算。

嵌入式微机保护测控装置，其计算能力有限，主要用来监视正常系统稳态下的运行状态。对于系统故障时可能出现的暂态变化过程不通过测控装置进行监视，故本文所述方法不考虑滤除系统故障时可能出现的衰减直流分量。虽然有很多方法可以较好的滤除恒定的直流分量，但是算法复杂，运算量较大，不适合实现。此外，我们也可以通过插值的方法保证在不同频率下每个整周期的采样点一致，但这样会消耗较多的资源。本算法既不需要硬件滤波、跟频，也不需要软件插值等复杂运算，在最低资源消耗的情况下，取得了较高的计算精度，非常适合运用于嵌入式微机测控装置中。目前，本算法以及该成功应用于某测控装置中，并在多个变电站现场长期稳定运行。

[1] 陈德树. 计算机继电保护原理与技术[M]. 北京: 水利电力出版社, 1992.

[2] 李晨, 张航, 张爱民, 等. 一种能滤除衰减直流分量的心递推离散傅氏算法[J]. 继电器, 2005, 33(17): 17-20.

[3] 邱海峰, 周浩. 非同步采样下电网谐波分析方法的探讨[J]. 继电器, 2008(1).

[4] 熊岗, 陈陈. 一种能滤除衰减直流分量的交流采样新算法[J]. 电力系统自动化, 1997, 21(2): 24-26.

[5] 张立华, 徐文立, 常成, 等. 一种适用于微机保护的新的递推DFT算法[J]. 店里系统自动化, 2000, 24(5): 28-31.

[6] 苏文辉, 李钢. 一种能滤去衰减直流分量的改进全波傅氏算法[J]. 电力系统自动化, 2002, 26(23): 42-44.

[7] 黄纯, 何怡刚, 江亚群, 等. 交流采样同步方法的分析与改进[J]. 中国电机工程学报, 2002, 22(9): 38-42. [8] 蔡菲娜, 左伍衡. 改进的双速率同步采样法及其傅里叶变换[J]. 浙江大学学报: 工学版, 2005, 39(3): 414-417.

The Method for Filtering the DC Component of Microcomputer Bay Control Unit with Non-synchronous Sampling

Wang Xiaoxiang Cheng Li Xiong Muwen
(NR Electric Co., Ltd, Nanjing 211102)

DC component is a vital factor which affects the accuracy of measurement. In order to filter out the DC component in the non-synchronous sampling, a method of filtering the DC component is proposed while using the RMS algorithm to calculate the effective value. This method uses the trapezoidal integration principle to divide sampling points in one cycle into integer points and points, and calculate the area of the integer points and the points to calculate the DC component, in the case of system frequency and sampling frequency deviation. Using the linear interpolation algorithm to obtain the sampling value of the fractional point. The proposed method does not need hardware frequency tracking circuit. Data window length is only one fundamental cycle. This method is suitable for a variety of computer protection and monitoring device. Actual device operation shows that this method can effectively remove the DC component and improve the measurement accuracy when the system frequency changes between 45～55Hz.

RMS; non-synchronous sampling; DC component; linear interpolation

王霄翔（1985-），男，工程师，硕士，主要从事变电站自动化系统，智能变电站自动化系统方面的研究。