基于最小生成树的低压配电网布局研究

谢建强

（国网桐乡市供电公司，浙江 桐乡 314500）



基于最小生成树的低压配电网布局研究

谢建强

（国网桐乡市供电公司，浙江 桐乡 314500）

低压配电网直接和广大用户相联系，是电力系统中极为重要的一环。但长期以来，由于低压配电网数量庞大且电压等级较低，其规划和布局未引起足够重视，常出现台区配变负载不均匀、供电半径过大、D类电压合格率偏低等状况。文章基于图论中的最小生成树及其所衍生出来的最短路理论，就区域负荷一定的情况下，如何合理确定配变安装点位置、如何科学规划低压配电线路走向等问题进行探讨，以期使农村台区建设达到既满足用户用电需求、又最大程度降低初投资额和运行线损等多赢目标。文章的算例表明，基于最小生成树的低压配电网布局方法操作简单、实用性强，不失为一种有效的电网规划层面的辅助决策方法。

最小生成树；低压配电网；图论；线损；初投资

组成低压配电网的核心元素是配电变压器和低压线路。二者的组合方式（即配变选址与低压线路走向）确定了低压配网的大致框架、初投资额、运行指标、可扩展性等各项要素。显然，配变选址和低压线路规划这两个层面相互耦合，但存在一定主次关系。由于配变承担着电力的转换和分配“职责”，是低压配网的源头，因此其是决策变量。

从本质上讲，配变选址要实现以最小的变电容量来满足最大的用电需求这一目标，同时为整个网络的建设经济性和运行可靠性打下基础。关于最小的配变容量确定（即配变定容），一般以拟建台区的负荷预测为依据，并考虑一定的宽裕度，本身不存在较大的讨论空间。文章重点研究：在配变位置确定过程中，如何同步考虑低压线路的建设，使整个网络的布局趋于科学和合理。

一般来说，配变选址分多源选址和单源选址两大类。二者的区别是一次性确定多个配变的位置还是单个配变的位置。鉴于多源选址中各配变之间存在复杂的耦合关系、非线性程度高，且目前农网台区以单电源放射式为主，因此文章将着重研究基于配变单源选址模式的低压配电网布局方法。

1　传统的配变单源选址方式

根据农网规划的相关导则，目前形成的配变单源选址方式主要有：

1）基于求解台区负荷重心的方法[1]

为了减少迂回供电，各级导则均要求配变布点需深入负荷中心。而最理想的负荷中心就是所谓的负荷重心。以图1为例，不妨令各负荷点的负荷值与坐标组合依次为｛P1，(X1,Y1）｝、｛P2，(X2,Y2)｝、…、｛Pn，(Xn,Yn)｝，则负荷重心的坐标可由式（1）确定。显然，在负荷重心处安装配变，从纯物理角度来说是非常合理的。

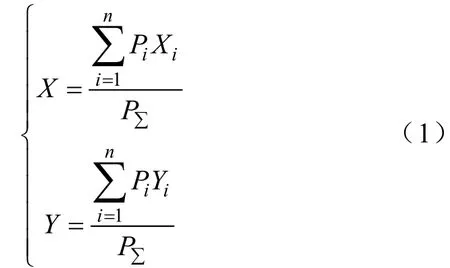
式中，X、Y为负荷重心的纵横坐标；P∑为各负荷点的负荷总加。

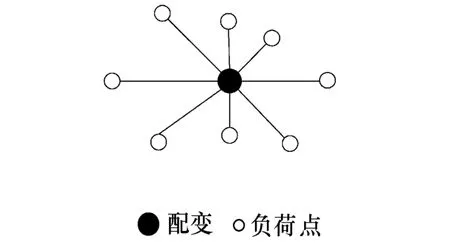
图1　负荷点分散情况下的负荷重心表示示意

2）基于运行费用最小的数学解析方法[2]

仍以图1为例（各负荷点的参数表示不变），设理想状态的配变安装坐标为（X,Y），则通过建立式（2）所示目标函数，借助计算机可求得X、Y值。

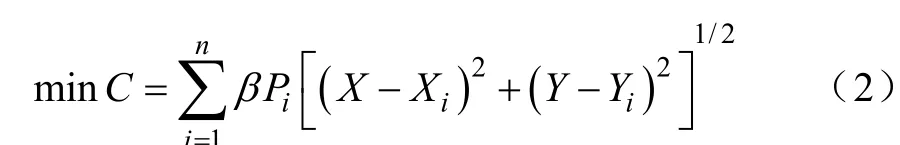
式中，β为单位负荷、单位距离费用系数。

2　问题的提出

从上一小节的论述看出，传统的配变单源选址方式契合“电源点要深入负荷中心”的重要原则，但在计算上未考虑实际低压线路走向所带来的投资和线损影响，另外在具体操作层面也存在诸多限制，不利于工程应用。下面就这些问题进行详细展开。

1）传统选址方式不符合低压配网实际结构。由前文内容可知，不论是负荷重心法还是数学解析法，均将低压配网简化为单一的电源点到负荷点的点对点直供网络（如图1所示）。这种网络在实际中很难应用，原因：①负荷点数量必然远大于配变出线间隔数量，因此不可能一个负荷点占用一个间隔；②低压线路实际走向受到周边地形、建筑物、线路走廊等影响，难以一条直线走到底；③每个负荷点均由电源点直供，必然造成导线的极大消耗。

2）传统选址方式中的坐标定位缺乏操作可能性。按照现有技术，坐标定位需要建立测量控制网、用到较为先进的测绘设备等，这对于建设周期短、建设数量大的低压配电网来说是难以承受的。

我们注意到，实际的低压配电网存在干线、支线、支干线等层次，其结构大致如图2所示。

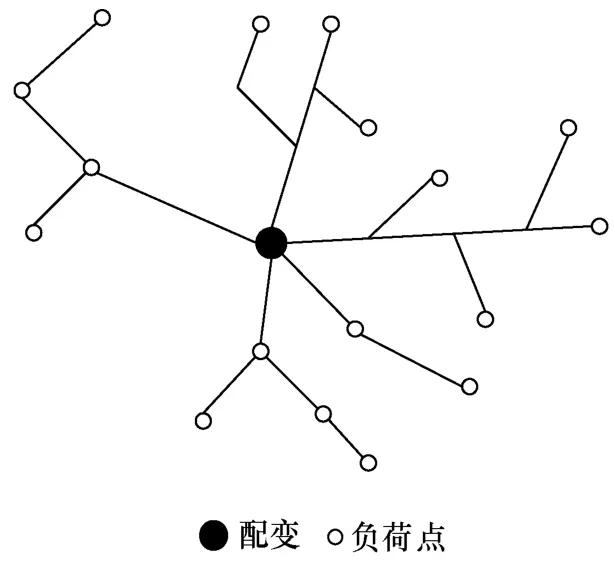
图2　实际低压配电网络的近似示意

因此，可以尝试运用图论的相关知识，将低压配电网等效为图论中的“图”：即将配变安装点和各负荷点对应为“图”的顶点，将低压线路对应为“图”的边集。然后进行寻优搜索（方法是找到“图”的一棵最小生成树，之后运用最短路理论确定配变安装位置和各条低压配电线路的大致走向），使配变选址与低压线路规划能够协同进行，从而避免传统选址方法的弊端。

3　最小生成树理论应用于低压电网布局

3.1实际低压电网与“图”的差异及相关处理

图论中的“图”由一定数量的顶点和边组成，各点、边只有位置或长度的不同，其他特性一致[3]。而实际低压电网的各自然负荷点存在容量差异、各段导线存在线径差异，可以说是“不平等的”。因此若要运用图论理论来处理低压配网优化问题，必须做到：

1）运用地理分割或归并的方法对自然负荷点进行区划和归集，形成一个新的负荷小块集合（要求该集合中的各负荷小块的负荷或容量基本相等），并粗略定出各负荷小块的地理中心，以此作为待优化低压电网等效于“图”的顶点，详见图3所示。

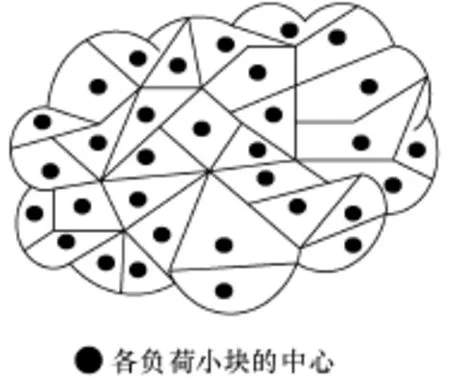
图3　待优化低压电网的负荷小块划分示意图

至于这种“人造”负荷小块的参考负荷值确定，可以视情况分别采取以下两种方法：①选择自然负荷点中不能分割的最大负荷值（如单个用户的电动机组）；②选择当地常用几类低压导线中通流量最低的导线所对应的可承受负荷。

2）初始时将待优化低压网络的所有线路均视为统一规格（如常用导线中通流量最低的导线），以此达到低压电网等效为“图”所要求的各边“平等”的要求。在运用图论程序产生目标网架后，再根据线路实际承担的负荷小块的数量来选择合适的线径（显得很有层次和条理）。

不难发现，经过以上 1）、2）的处理，可以规避：①因自然负荷点过多而造成的目标网架过于复杂；②因自然负荷点容量的不同而造成对目标网架线路线径选择的困难。

3.2具体建模

首先将图3展示的各负荷小块中心进行两两相联，形成一个所谓的无向完备图，如图4所示。并根据大致估测得到各边的长（也称“权”）。

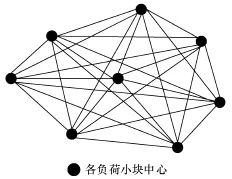
图4　连接各负荷小块中心的无向完备图示意

其次运用相关算法（最小生成树算法），从图4的所有支撑树（连通而无圈的图称为支撑树）中找到树权最小的那一棵。

最后，对已经找到的最小生成树，计算“树”的任一顶点到其余顶点的最短路之和，形成一个和值集。而该和值集中最小的和值所对应的顶点就是最佳的配变安装点，组成该和值的各边就是低压配网的布线路径。

3.3最小生成树算法设计

最小生成树的经典算法有 Kruskal算法等，笔者结合低压配网实际（节点多、分之多）进行最小生成树算法改进。

1）首先将无向完备图的各边按一定规则进行排列。考虑操作简便性，不妨定规则为“按边长递增”。对于一个含有q条边的图来说，有

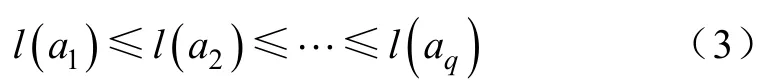
式中，l(ai)（i=1，2，…，q）为编号为ai的边长。

2）按边长从小到大，检查不构成回路但又能将图连通的最少边集组合。

令e1=a1，e2=a2，测试a3，若a3与e1、e2不形成回路，则令 e3=a3，如果 a3与 e1、e2形成回路，则测试 a4（不再考虑将 a3纳入最小生成树）；如果a4与 e1、e2不形成回路，则令 e3=a4，否则测试 a5（不再考虑将 a4纳入最小生成树）。如此往复，直到找出含 e1，e2，…，ep等 p条边的连通图为止。那么｛e1，e2，…，ep−1｝就是一棵最小生成树。

最小生成树中的最短路定义：在最小树T中，从顶点U到顶点V的最短路径（权值最小）P*(U,V)。最短路算法一般参照Floyd算法[4]，限于篇幅，文章不再详述。

4　算例分析

以浙江桐乡为例：某乡村欲在2015年新建一个台区，台区的供电范围基本确定，今后3年的负荷预测已经完成。通过对供电区域的划分，得到类似图3所示的负荷小块，并且测算出各负荷小块中心点之间的距离，见表1。

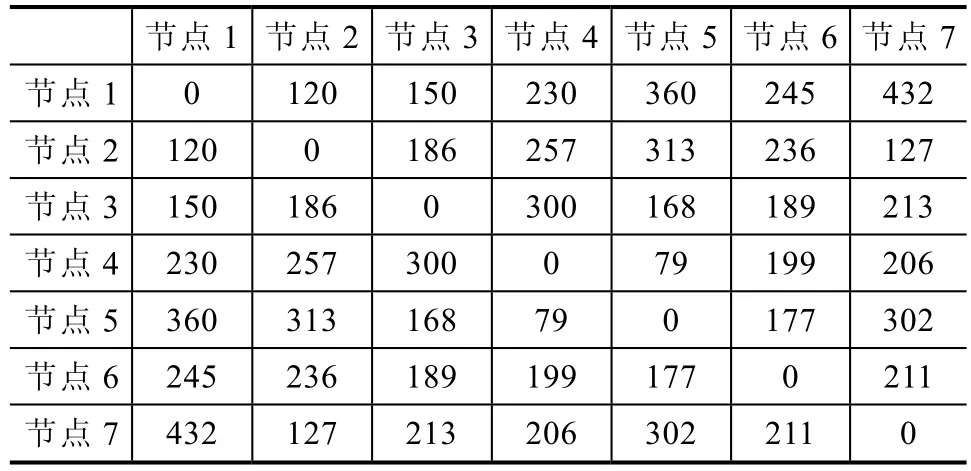
表1　某拟建台区各负荷小块之间的距离列示/m

根据表 1，首先画出由7个负荷小块的中心两两互连而形成的无向完备图（图略），依照文章设计算法，找到该无向完备图的一棵最小生成树，如图5所示。图5展示了最小生成树的顶点集和边集情况。

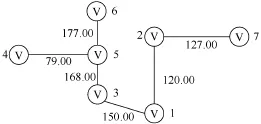
图5　依据算例数据所产生的的最小生成树

根据 Floyd算法，得到最小生成树的Floyd矩阵，见表2。

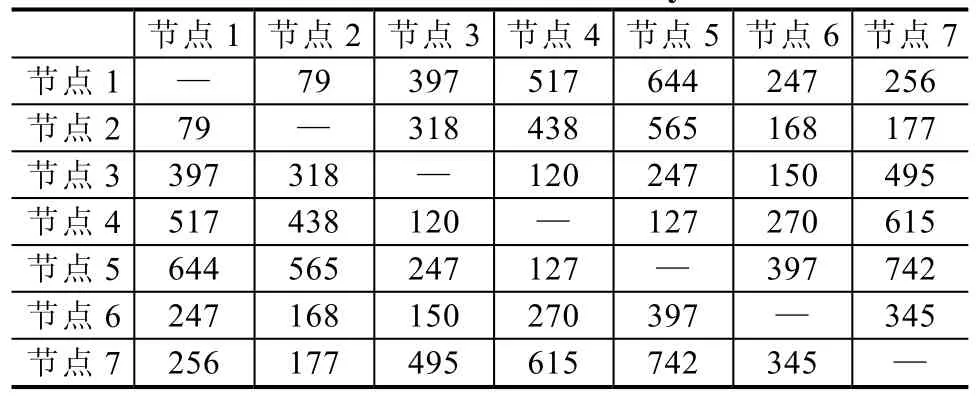
表2　依据算例数据产生的Floyd矩阵/m

对该表作简单统计，即可知节点6至其余各节点的“最短距离”之和为最小，按文章所建模型，确定第6节点处（即编号为6的负荷小块中心处）作为配变安装的地点。而图5所示网络可作为低压线路网架规划的辅助决策。

表3所示为按传统方法和最小生成树方法比对的算例工程的初投资、年运行损耗测算情况。

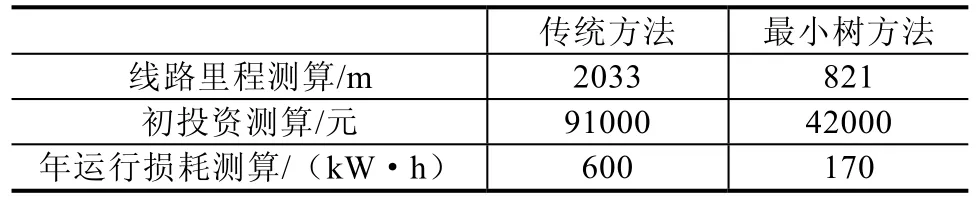
表3　算例工程的初投资、年运行损耗比对/m

5　结论

低压配电网纷繁芜杂，进行科学、精确规划是较为困难的。文章从低压配电网的结构特征出发，创造性地利用图论的有关理论，将低压配电网优化布局问题等效为图论中最小生成树及最短路的搜索问题，从而在理论上实现了配变选址与低压线路规划协同优化的目标。算例结果表明：该方法操作简便、工作量小、实用性强，在很大程度上达到了台区建设初投资最小化和线损最优化的效果，因此对低压配电网建设具有较大的辅助决策意义。同时，根据中压配网的结构特性，文章所构建的方法显然也可在中压配网建设中酌情推广。

当然，该方法在优化配网布局时，对负荷跃变、线路走廊困难等实际可能存在的问题是简化处理的，这需要专家知识和经验的补充。

[1] 刘巍. 变电站站址优化与配网开关优化配置的研究[J]. 郑州大学学报, 2014, 31(2): 132-135.

[2] 王朝瑞. 图论[M]. 5版. 北京: 北京工业学院出版社, 1987: 48-58.

[3] 原河峰, 杨丽徙, 章健. 以最优化理论进行农村电网规划（一）[J]. 农村电气化, 1994, 36(6): 2-4.

[4] 卢开澄. 图论及其应用[M]. 8版. 北京: 清华大学出版社, 1981: 160-165.

Study on the Low-voltage Distribution Networks based on Minimum Spanning Tree Layout

Xie Jianqiang
(State Grid Tongxiang Power Supply Company, Tongxiang, Zhejiang 314500)

Low voltage distribution networks and users directly linked to is extremely important link in the power system. However, due to the huge number of low-voltage power distribution and low voltage level, the planning and layout does not pay enough attention to, common area with the same load is not uniform and the RADIUS is too large, class-d power supply low voltage conditions. Based on minimum spanning tree in a graph theory and the theory derived from the shortest, load under certain situations, how to determine distribution transformers installation point, how to plan low-voltage distribution line and other issues were discussed, with a view to bringing the rural area construction to meet user demand, minimizing the initial investment and operation line loss, a win-win goal. Article example shows that low voltage distribution network based on minimum spanning tree layout is simple and practical, it is an effective method for decision of power grid planning.

minimum spanning tree; low voltage distribution network; graph theory; line loss; initial investment

谢建强（1982-），男，工程师，大学学历，主要从事电力系统的运维。