新型同步磁阻电机电感参数的测量

叶 芃

（中国质量认证中心福州分中心，福州 350008）



新型同步磁阻电机电感参数的测量

叶 芃

（中国质量认证中心福州分中心，福州 350008）

本文在介绍了应用直接负载法测量同步磁阻电机交、直轴电感原理的基础上，提出了一种利用光电脉冲编码器精确测量电机稳态运行时电压合成矢量与转子 d轴的夹角，并结合相关公式，计算求得交、直轴电感值的方法。该方法对同步磁阻电机交、直轴电感的测量有较高的准确度。样机试验检测了同步磁阻电机在不同负载下的交、直轴电感值，并与有限元仿真计算的结果进行比较，两者比较吻合，验证了这种方法的可行性和准确性。

同步磁阻电机；电感参数；直接负载法

新型同步磁阻电机（SynRM）的定子的结构与一般异步电机相同，而转子采用特殊结构的硅钢片叠压而成（如图1所示），没有鼠笼绕组或永磁体，其产生的电磁转矩仅有磁阻转矩。由于同步磁阻电机不存在着转子损耗，与一般异步电机相比具有更高的效率、较低的温升和更大的功率密度，为此得到许多国内外学者的关注[1]。

图1　1/4转子结构图

由于同步磁阻电机转子不存在着励磁源，电机磁路的饱和程度取决于定子绕组的电流，因此负载的变化将会影响磁路的饱和程度从而改变电机的交、直轴电感[2]。同步磁阻电机的电磁转矩与交、直轴电感差值成正比，因此电感测量的准确性将影响对同步磁阻电机的控制。文献[3-4]采用P-Q圆法进行电感测量，此法的前提是将电感参数视为定值。由于同步磁阻电机电感随负载变化较大，因此测量得到的参数只适用于某个固定的运行点。文献[5]采用电压积分法测量电感，该法忽略了磁路交叉饱和的影响，且无法测量不同负载下的电感。文献[6-7]利用直接负载法，并通过在被试电机转子上安装一个每转产生一个脉冲的编码器，离线分析出功角，然后进行电机交、直轴电感的计算。本文采用直接负载法测量同步磁阻电机的电感，并设计了一套利用光电脉冲编码器实现转子位置精确测量的电路，可以在线测量电机稳定运行时合成电压矢量与转子的d轴的夹角，从而计算出电机的交、直电感。该方法考虑了磁路的交叉饱和影响，可实现不同负载下的电机交、直轴电感参数的测量。为了验证此方法的对电感的测量精度，本文对样机进行了有限元仿真计算和实物试验，给出了理论值和实测值的比较分析结果。

1　电感测量原理及实现

不计铁耗时，同步磁阻电机在同步旋转dq坐标下的矢量图如图2所示。图中Is和Us分别为三相合成电流矢量和电压矢量，Rs为定子电阻，Id和 Iq分别为电流的交、直轴分量，Xd和Xq分别为交、直轴电抗，ϕ 为功率因数角, γ 为电流矢量与d轴夹角，δ 为电压矢量与q轴夹角。

图2　同步磁阻电机矢量图

根据矢量图得

将式（3）、式（4）代入式（1）、式（2），得

由此可知，要求得同步磁阻电机的交、直轴电感参数，可以通过测量电机三相合成电压矢量Us、电流矢量 Is的大小、定子电阻 Rs、功率因数角ϕ、角频率ω 以及电压矢量与 q轴的夹角δ，并利用式（6）、式（7）计算得到。其中，前5个参数可通过电参量仪表测得，而角度δ 无法直接测得。

由于当A相电压达到最大值时电压矢量Us在空间上的位置正好与A相轴线重合，可以利用这一特性来进行角度δ 的测量。为此本文设计了一套测量装置，即在电机转子上安装一个光电脉冲编码器来记录转子的位置信息。当电机处在静止状态时使电机A相轴线与转子d轴对齐，并将编码器脉冲计数值清 0；当电机转动后，则任意时刻编码器的脉冲计数值即为转子 d轴与定子 A相轴线夹角的对应值。电机带载稳定运行时，电压矢量Us与d轴之间的夹角是固定的。当A相电压达到最大值时，Us正好在A相轴线上，此时读取的编码器脉冲数值即为Us与 d轴对应的夹角，减去90°即为角度δ。由于相电压最大值时刻不好检测，可通过检测线电压过零时刻进行转换计算。测量的具体步骤如下。

步骤1：使A相轴线与d轴对齐。将电机三相绕组按图3形式连接，并给电机绕组加直流电压，此时三相绕组中的电流关系为Ib=Ic=−0.5Ia，电流矢量Is正好在A相轴线上。依靠电机的磁阻转矩d轴与A相轴线自动对齐，并将编码器脉冲计数器清零。

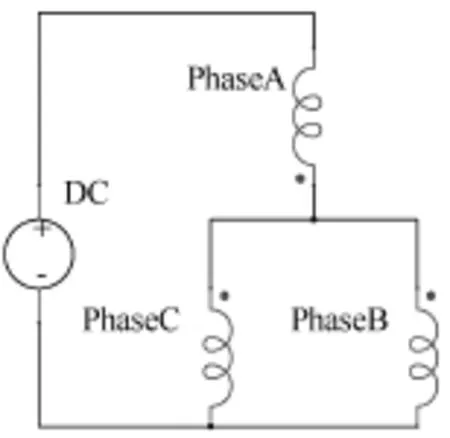
图3　d轴定位的定子绕组接线示意图

步骤 2：线电压 UAC过零时刻编码器脉冲计数值的读取。通过图4电路将UAC转换为方波U0。通过一个由 DSP单片机组成的测试装置，利用 DSP的捕获单元，将产生的方波信号U0送入其捕获信号输入引脚，在 U0上升沿时刻读取编码器脉冲计数值，记为T1，对应的角度即为β。

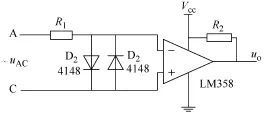
图4　电压过零检测电路

步骤 3：角度δ计算。如图5所示，U0上升沿滞后UAC最大值时刻90°，而A相电压UA超前UAC30°。稳态时A相绕组的相量图与图2所示的矢量图是重合的，UA与Us重合，如图6所示。A相电压相量UA超前于AC线电压过零时刻120°，由此可计算得到角度δ=120−90−β。

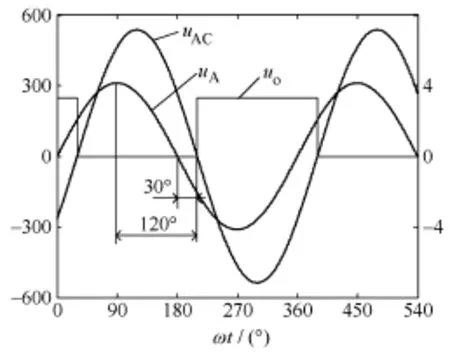
图5　电压过零检测波形示意图

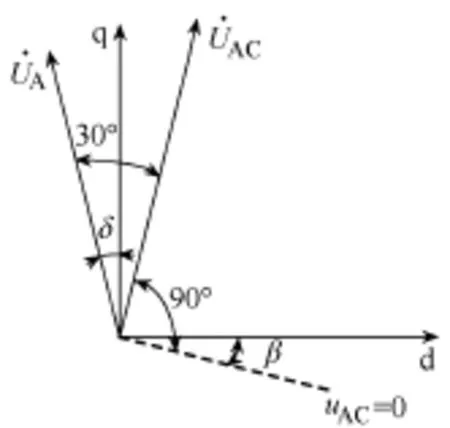
图6　电压相位关系

通过上述方法测量得到角度δ，再通过电参量仪表测得其他五个参数，代入式（6）、式（7）就可求得同步磁阻电机在不同负载下的交、直轴电感。

2　交直轴电感的有限元计算

同步磁阻电机的磁链方程为

由于通过有限元的仿真分析，能够方便地获取电机的电流和磁链数据，因此可根据式（8）、式（9）可求出交、直轴电感值。

仿真时采用瞬态场，施加电流源激励，转速设置为同步转速。图7为按照实际电机结构建立的有限元模型。图中灰色标识的绕组为A相绕组，此刻A相绕组中的电流为峰值，三相合成电流矢量的空间位置与A相轴线重合，转子d轴与电流矢量夹角γ=60°。仿真时通过设置初始时刻转子的位置角来改变电流矢量与d轴的夹角γ。图8为仿真得到的三相电流和磁链波形，将三相磁链、电流数据导出，根据式（10）、式（11）计算得到对应的d、q轴分量，代入到式（8）、式（9）取平均值即可得到交、直轴电感Ld和Lq。其中θ 为转子d轴与A相轴线的夹角。

图7　电机有限元模型

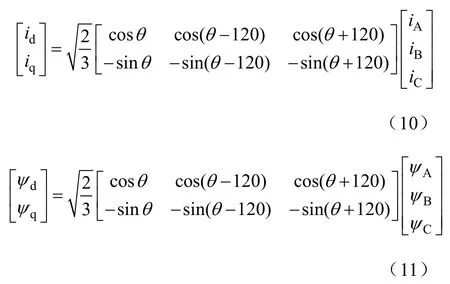
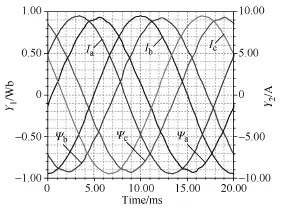
图8　三相电流、磁链仿真波形

3　实验分析

新型同步磁阻电机被试样机的相关数据见表1。样机定子相绕组电阻为2.2Ω。实验时用直流电动机将样机拖至同步速，然后切入电网运行；利用电参量仪表测出不同负载时样机的相电流、线电压、角频率以及功率因数；通过电压过零检测装置检测线电压UAC过零时刻的转子位置角度，求出对应的角度δ，即可计算出样机的交、直轴电感值。电感测量的实验平台如图9所示。这里光电脉冲编码器与被试电机转子轴相连接，编码器 A、B相两组输出脉冲的分辨率为 2000p/r。通过 DSP的脉冲编码电路模块处理可使脉冲分辨率增至8000p/r，因此机械角度的测量精度可达360/8000=0.045°/p。

有限元仿真分析时根据实测得到的功角δ，计算电流角γ，设置与实测电流具有相同大小和角度γ 的电流激励进行计算。

表1　同步磁阻电机数据

图9　实验平台

表2　实验与仿真数据对比

表2为不同负载下电感的实测值与仿真值的对比。从表中可以看出直轴电感的实测值与仿真值较为吻合，相对误差小于5%；交轴电感的实测值与仿真值误差较大，介于 5%～9%之间。由于有限元仿真时采用的是 2D模型，不考虑端部漏感的影响，导致仿真的电感值会比实际计算值偏小。另外由于实测电感时忽略了铁耗的影响，也导致了交、直轴电感的实测值与仿真值的偏差。

同步磁阻电机的转矩表达式为

由于根据式（6）、式（7）计算电感时没有扣除铁耗的影响，因此利用式（11）计算电磁转矩时其对应的电磁功率包含了铁耗部分。另外该电磁转矩还包含了机械损耗和杂散损耗所对应的转矩，因此直接根据式（11）计算得到的电磁转矩会比实测转矩偏大。表3为利用实测电感参数代入式（11）计算并扣除铁耗、机械损耗和杂散损耗后得到的转矩与实测转矩的对比，其中铁耗、机械损耗和杂散损耗取电机额定功率的3%，对应的转矩为0.57N·m。从表中可以看出转矩计算值与实测值的相对误差较小（±2%以内），说明了实测电感的准确性。

表3　计算转矩与实测转矩对比

4　结论

本文采用直接负载法并利用光电脉冲编码器测量电压矢量与q轴的夹角来计算新型同步磁阻电机的交、直轴电感。本方法适用于同步电机在不同负载下的交、直轴电感测量，测量结果考虑了磁路饱和对电感的影响。把有限元仿真计算得到的电感参数与实测结果进行比较，两者较为吻合；利用实测电感计算得到的转矩与实测值误差也较小，验证了本文所提出的同步电机交、直轴电感测量方法的可行性和准确性。

[1] Lipo T A. Synchronous reluctance machine: A viable alternative for a.c. drives[J]. Elect. Mach. Power Syst., 1991, 19(6): 659-671.

[2] 周浩, 严欣平, 卢权华, 等. 转子结构对同步磁阻电机电感参数及转矩的影响[J]. 微电机, 2013(9): 22-26.

[3] 程明, 周鹗. 测量磁阻电机同步电抗的P—Q圆图法[J]. 微特电机, 1990(2): 2-5.

[4] 游琳娟, 吴汉光. 磁阻电机参数测定研究[J]. 微特电机, 2001(1): 29-31.

[5] 张飞, 唐任远, 陈丽香, 等. 永磁同步电动机电抗参数研究[J]. 电工技术学报, 2006, 21(11): 7-10.

[6] Gieras J F, Santini E, Wing M. Calculation of synchronous reactance of small permanent-magnet alternating current motors comparison of analytical approach and finite element method with measurements[J]. IEEE Transactions on Magnetics, 1998, 34(5): 3712-3720.

[7] 张健, 刘明基, 陈伟华. 自起动永磁电机电抗参数的测试[J]. 电机与控制应用, 2010(8): 14-18.

Measurement for Inductance Parameter of New-style Synchronous Reluctance Motor

Ye Peng
(Fuzhou Branch of China Quality Certification Center, Fuzhou 350008)

Based on the measurement principles of the direct and quadrature axis inductances of synchronous reluctance motor with direct load method. The paper proposes a method to measure intersection angle between synthesizing voltage vectors and rotor d axis with photoelectric encoder and then to calculate direct and quadrature axis inductances value in combination with the relative equations. The method has relative high precision of measurement for direct and quadrature axis inductances of synchronous reluctance motor. The experiment for the direct and quadrature axis inductances values of the prototype under the different loads is made. Test results are compared with the values of finite element simulation of the same motor and results are identical, so the method is proved to be feasible and precise.

synchronous reluctance motor; inductance parameter; direct load method

叶 芃（1983-），男，福建仙游人，本科，工程师，现工作于中国质量认证中心福州分中心。