基于混合优化算法的配电网动态重构研究

时慧喆刘志鹏钟文强

（1. 山东科技大学电气与自动化工程学院，山东 青岛 266590；2. 海南电网公司电力调度控制中心，海口 570203；3. 国网山东平度供电公司，山东 平度 266000）



基于混合优化算法的配电网动态重构研究

时慧喆1刘志鹏2钟文强3

（1. 山东科技大学电气与自动化工程学院，山东 青岛 266590；2. 海南电网公司电力调度控制中心，海口 570203；3. 国网山东平度供电公司，山东 平度 266000）

本文提出了一种混合了混沌粒子群与教学优化的算法来解决配电网动态重构问题。建立以网络损耗最小，开关操作次数最少的运行费用模型。将配电网络的损耗和电压偏差这两个指标通过归一化处理形成一个综合指标，并设定最大标准差及系统最大重构次数，确定重构时段。所提出的方法结合了混合粒子群优化算法和教学优化算法的特点成为了一种更有效率的全局优化算法。为了在配电网动态重构中可以动态调整惯性参数，在一般的粒子群算法中引入了混沌理论，同时具有教学优化的混合算法可以保证初始种群的多样性和防止过早收敛，提高了算法寻优的能力。最后使用了IEEE 33节点配电网测试系统证明了所提算法的合理性与有效性。

配电网动态重构；重构时段；混沌粒子群算法；教学优化算法

配电网重构问题是一个复杂的开关组合优化问题，配电网重构的基本目的包括减少网损，降低运行费用等。配电网的重构一般是通过改变分段开关和联络开关的开闭状态从而改变配电网的网络结构[1-2]。在配电网重构操作时，要确保配电系统的辐射状结构和保证所有负荷的供电。因此，配电网中的分段开关和联络开关的数量越多，重构有可能形成的结构就越多。文献[3]运用遗传算法解决配电网的重构问题，但此过程中，可能产生很多不满足运行约束的不可行解。文献[4]采用扩展生长树法，有效避免了环网的形成，但这种方法的计算量大，不具有通用性。文献[5]提出了粒子群算法粒子位置的新规则，求解配电网重构时，加入了禁忌算法用来解决早熟的问题。文献[6]提出一种混合粒子群算法，主要特点是将二进制的粒子群算法和离散的粒子群算法相结合。

本文提出了一种混合算法来解决配电网的动态重构问题，该算法将混沌粒子群算法和教学优化算法混合在一起，从而使得新算法同时具有教学优化算法和混沌粒子群算法的优点。在满足系统运行约束条件的同时，实现以系统运行费用最小为目标的配电网动态重构。

1　配电网动态重构问题

负荷是随着时间动态变化的，所以在理论上动态重构的方案应该随着负荷的波动而不断变化。然而，受到分段开关和联络开关的使用寿命，操作费用等因素的影响，无法对配电网频繁的进行重构操作。所以，寻找更合理、有效、经济的算法是解决配电网动态重构问题的关键。

1.1配电网动态重构数学模型

本文的配电网动态重构考虑到经济效益为基础，考虑到网损费用、开关操作费上的因素，建立最小目标函数，即

式中，f1( t)为网损费用；E1( t)为时段t的电价；sc,t是在t时段开关c开闭状态，开关c断开与闭合状态分别用0和1表示；rb为支路b的电阻；Pb( t)和Qb( t)分别为在t时段流经支路b的有功和无功；Ub为在t时段支路b的末端节点电压；E2( t)为开关单次操作的费用；Nb为网络支路总数；NS为可操作开关的总数；M为时段划分后的时段总数。

1.2约束条件

1）支路容量约束

2）配电网潮流约束

式中，Pti和Qti是分别为t时段注入节点i的有功和无功；Uti和 δti分别是t时段节点i的电压和相角；Yij是节点 i、j之间的导纳矩阵；θtij是 t时段 i、j之间的相角。

3）开关的操作次数约束

式中，sc. t表示开关c在t时段的开闭状态；sc.max和smax分别表示单个开关的操作次数上限和所有开关的操作次数上限。

4）母线电压约束

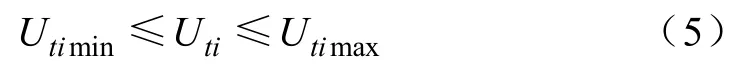
式中，Utimin和Utimax分别表示节点i电压在t时段的最小值和最大值。

5）网络拓扑约束

配电网通常是闭环设计，开环运行，因此须要在重构后保持配电网的辐射状结构，并且没有任何孤岛，即式中，gn和G分别表示第n次重构的网络结构和配电网重构后可能出现的辐射状网络结构集合。

2　配电网动态重构的时段划分

2.1配网运行指标

1）网络损耗

在配电网络重构当中，尽可能的减小网络损耗是提高配电网络经济运行的关键环节。

将网络损耗作为评价指标 g1，如式（7）：

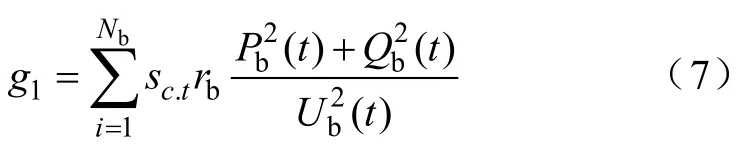
2）电压偏差

电压质量是经济性的重要指标，如果电压偏差较大将会直接影响用户正常用电，同时也会对保护设备、电器造成严重伤害。

将电压偏差作为评价指标g2，如式（8）：式中，Nbus为配电网络中全部节点数的数量；UiS为节点i处实际电压；UiN为节点i处额定电压。

3）配网运行综合指标函数

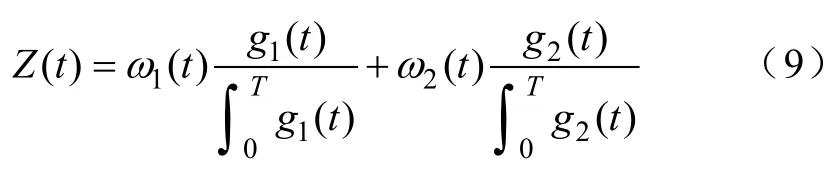
根据上述给出的2个指标按照所划分不同时段进行归一化，如式（9）：式中，ω1(t)、ω2(t)分别为网络损耗、电压偏差加权系数，根据折算后经济收益的占比、网络运行情况做调整；T为重构总时间。

2.2重构时段划分

根据上述的系统运行综合性指标，将T划分为M个时段，将不同时段的综合指标进行结构偏移处理，如式（10）：

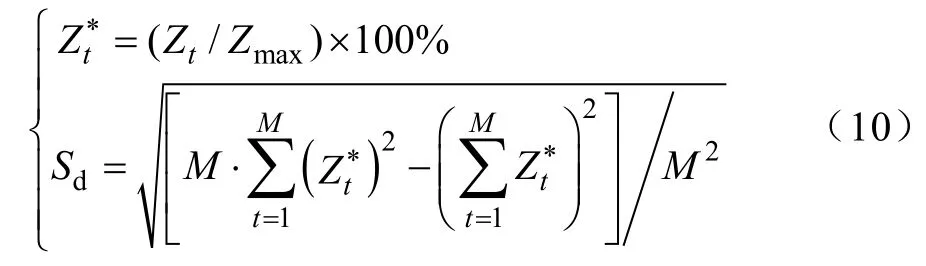
Sd反应了各时段综合指标波动情况，从而反应系统的运行状况。可以在一天中划分出的各时段进行计算，得到各时段的综合评价指标偏移度，并设定适合的Sdmax最大标准差，并对各时段偏移进行划分。具体划分步骤如下：

1）计算24个时段的综合指标偏移度，并设定Sdmax。

2）将第1、2个时段划入重构时段Ⅰ，计算偏移度，如果超过 Sdmax则将第2时段划入重构时段Ⅱ，反之留在重构时段Ⅰ。

3）如果将第2时段留在重构时段Ⅰ，则将第3时段划入重构时段Ⅰ，重复步骤 2。如第2时段划入重构时段Ⅱ，则将第3时段划入重构时段Ⅱ，计算偏移度，如果超过Sdmax则将第3时段划入重构时段Ⅲ。依次类推，完成所有自然时段的重构时段划分。

由于配电网系统在实际运行过程中，无法同时满足最大重构次数的约束与最大开关操作次数等约束，因此Sdmax的取值会影响到划分出的重构时段数，通过迭代对Sdmax进行修正，即

式中，CN为计算出的重构时段数；Cmax为允许的最大重构时段数；k为迭代次数。

3　混沌粒子群优化算法

3.1传统粒子群算法

粒子群优化是通过模拟鸟群觅食行为而发展起来的一种基于群体协作的随机搜索算法，算法不断更新种群在搜索时的速度和位置[7]。本文中，控制变量表示为

联络开关（Tiei）与分段开关（Swi）形成的回路，通过开关的开、闭组合来保持回路的辐射状结构。

现在假设开关的控制变量X的状态如下：

一个粒子的搜索空间状态可以由位置和速度两个因素决定由以下方程表示：

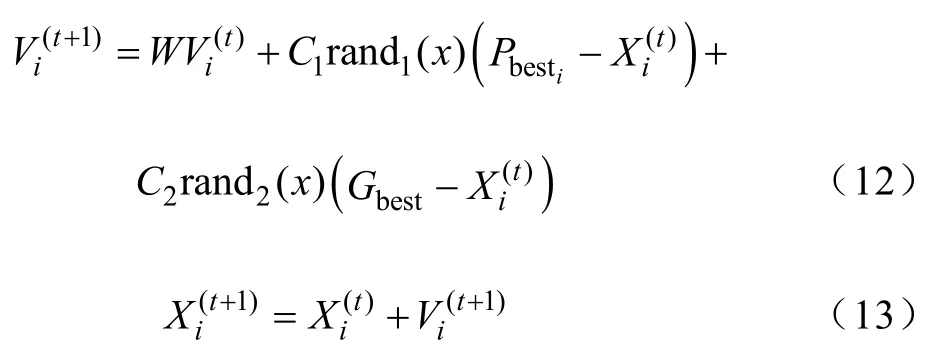
3.2惯性权重的混沌方程

惯性权重因子用来控制粒子原有的速度对当前速度的影响，惯性权重W较大对全局搜索有利，惯性权重W较小对局部搜索有利。

虽然，粒子群算法有很多优点，概念简单，容易实现，存储要求低，与其他优化算法混合使用较简单。但它容易产生不合适的收敛结果和陷入局部最优解。因此，适当的调整算法中的参数对发现最优解非常重要。

在本文中，每次迭代时惯性权重因子动态调整方程为

苹果幼树枝量和花芽形成能力是早产、稳产的保证。目前，有不少措施可以促进幼树尽快扩大枝量、尽早大量形成花芽，以尽早形成产量。目前传统的方法都存在这样那样的缺点。寻求新的、更加安全高效的药剂是目前苹果矮砧现代栽培模式的需求。通过上述试验我们发现，发枝促花剂有效提高了当年定植小树的成枝能力，显著提高2年生树侧枝芽萌发率，抽生新枝多为中短枝条，孕育大量花芽，能够提早1～2年进入结果期，并且树势保持中庸，为早产打下坚实的基础。

式中，CW(t)表示混沌惯性权重在第t次迭代时的值；W(t)是惯性权重因子；B(t)表示在第t次迭代时的混沌参数。B(t)的值是由混沌系统（logistic函数）来决定，其公式如下：

式中，μ为控制参数，其值的范围是[0,4]；μ的变化受到B(t)的影响，B(t)的值可能是常量或变量。当μ=4且B0∉{0,0.25,0.50,0.75,1}时，式（15）中的μ值没有随机性，未体现出混沌状态。

4　教学优化算法

教学优化算法是受到老师与学生关系的启发而产生的一种有效率的种群算法[8]。这种算法中种群是一个班的学生，变量是所提供的课程。老师是班里知识最丰富的人，并且将知识传授给班里的其他学生从而提高班里的成绩，学习效果由班里的平均成绩决定。学习过程由两部分组成，“教学部分”和“学习部分”。

4.1教学部分

老师通过教学提升班里同学的知识水平，但是实际上能达到哪一种水平取决于班里同学的学习能力。教学部分用方程表示为

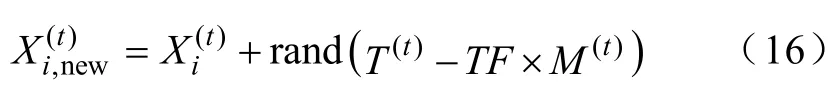
式中，TF表示学习因子，其取值为在1到2之间的随机数；T(t)代表经过t次迭代后学生中成绩最好的；M(t)是班里成绩的平均值。如果的值比更好，那么取的值。

4.2学习部分

学生通过教学部分和学生之间的相互学习来获取知识。相互学习的方程表示如下：

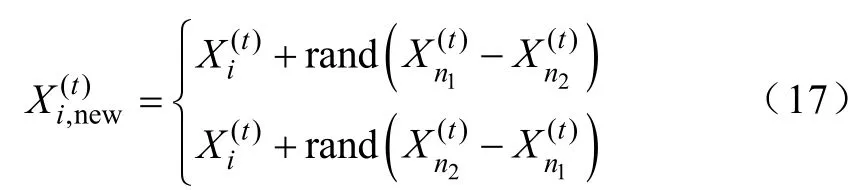
式中，n1和 n2为随机选出两个学生，其中 n1≠n2≠i，如果f( Xn1)＜f( Xn2)表示学生xn1优于学生xn2，那么向xn1靠近，反之学生xn2优于学生xn1，则向xn2靠近。学习阶段过后，比较与当前解Xold，如果优于Xold，则接受。

5　混合算法

将混沌粒子群算法与教学优化算法结合的主要目的是使得新算法具有这两种算法的优点，从而提高搜索能力找到最优解。混合算法可保证初始种群的多样性，限制过早收敛，收敛速度快等特点。

混沌粒子群—教学优化算法在配电网动态重构问题上的步骤如下：

第1步：输入配电系统的基础数据。

第2步：根据网络的初始结构和负荷用式（7）和式（8），计算不同时段的1g、2g。

第3步：设定重构次数的最大值Sdmax，并将一天划分为若干个重构时段。

第4步：判断是否进入所划分的时段；如果没有进入，则执行第14步。

第5步：生成初始种群，混沌粒子群—教学优化算法中所产生的初始化种群为形式如下：

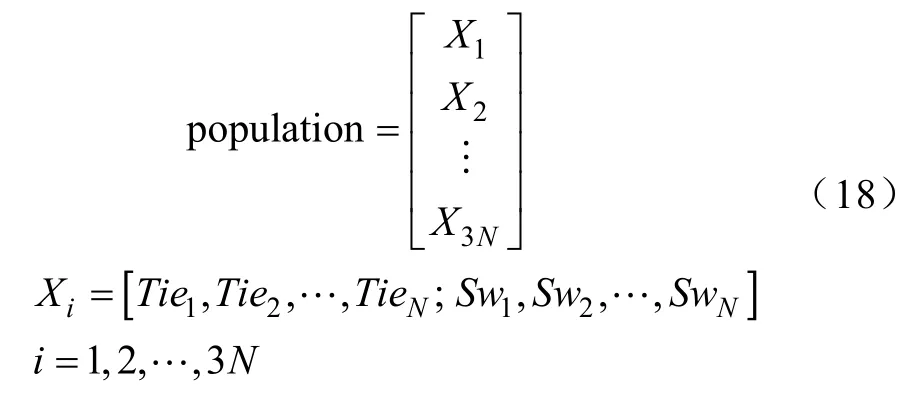
第6步：使用所建立的目标函数（式（1））计算初始种群中的每个个体的值。

第7步：按适应度大小降序排列初始化种群中的个体。

第8步：依照排列顺序选择前2N个个体作为混沌粒子群算法的初始种群；剩余大小为N的种群作为教学优化算法的初始种群。

第9步：用式（14）更新惯性权重。

第10步：选出最适应目标函数的粒子作为Gbest，同时更新相关种群的位置信息。每代新种群都与相关的粒子 Pbest相比较；如果有更好的粒子位置，则更新Pbest的位置。

第11步：选出对目标函数适应度较差的种群作为教学优化算法的初始种群，相关种群通过式（16）和式（17）更新。

第12步：混合从混沌粒子群算法和教学优化算法中分别得到的个体。

第13步：当群体的全局最优解在几次迭代后都不变时，判断算法收敛，停止计算，输出结果；否则返回步骤8。

第14步：计算在本次重构时段内系统的网损。

第15步：判断重构时段是否结束。如果结束输出结果；没有结束返回第4步。

6　算例分析

为了证明提出的算法在配电网动态重构中的有效性，采用了IEEE 33节点配电网测试系统（如图1所示）进行了验证。配电网重构之前以1h为单位长度划分24个自然时段，各节点的负荷数据可参照文献[9]，假设每个时段内负荷恒定，每个开关操作次数不超过3次，所有开关总的操作次数不超过15次，开关每动作一次的费用为5元，网损中电费为0.5元/kW·h。

设定系统重构的最大次数不超过3次，得到对应的配电网重构时段为 1∶00—8∶00，9∶00— 21∶00，22∶00—24∶00。根据划分出的时段，使用本文所提出的混沌粒子群-教学优化算法得出的重构方案见表1。

图1　IEEE 33节点配电系统

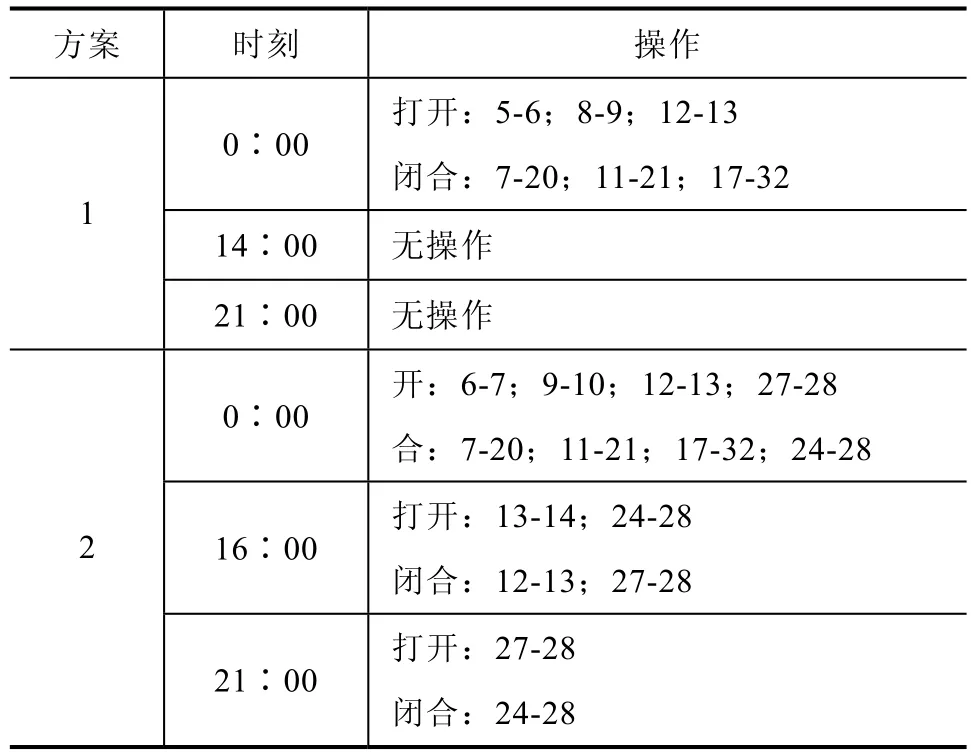
表1　重构方案

实际的费用包括配电网本身的损耗费和分合开关的操作花费。在配电网重构之前，整个配电网1天的损耗为2875.83kW，总费用为1437.92元。

从表2可以看出，方案1能使网络损耗降到2075.3kW，降幅约为27.8%，总费用为1067.65元。方案2能使网损耗降到2032.5kW，降幅约为29.3%，总费用为 1086.25元。将开关动作的花费用考虑在内，可确定方案1为实际使用的方案。

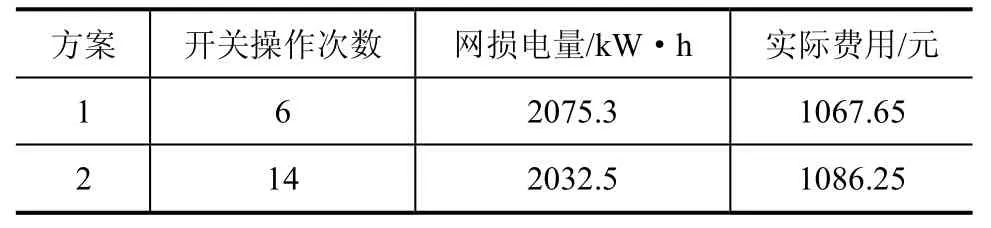
表2　两种方案的总费用

在用本方法进行重构后，系统在各时段的网损有了明显的降低，如图2所示时段1∶00—8∶00，在此时段配电网中的负荷较少，重构后网络损耗降幅小。进入9∶00—21∶00时段后，网损降幅较大，网损情况有了明显的改善。

最后，使用本文所提算法与其他算法所得出的电压偏差，最小电压，网损及迭代次数进行了对比（见表3），可以看出所提算法优于其他算法。

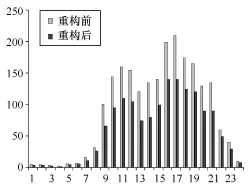
图2　网络损耗在重构前后的对比

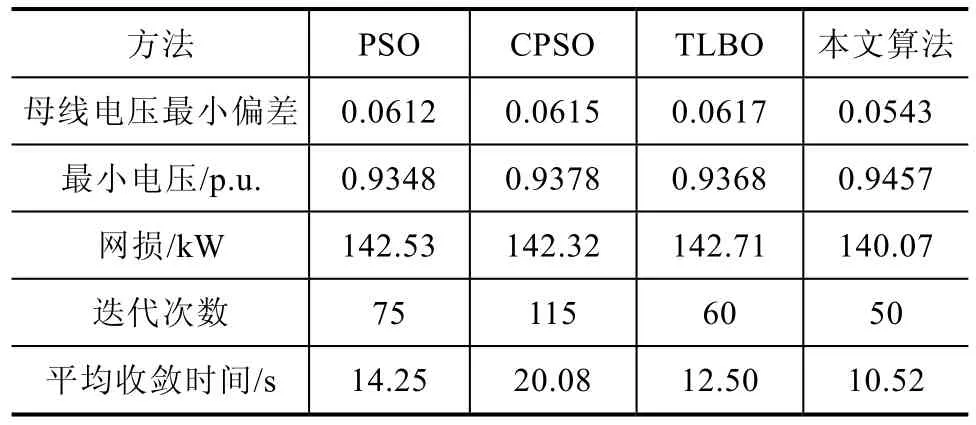
表3　不同算法的比较

7　结论

本文提出了基于混沌粒子群优化算法和教学优化的混合算法来解决配电网的动态重构问题；并对所建立的配电网动态重构的模型、约束条件等进行了相关的修正。最后，使用了IEEE 33节点配电网测试系统进行仿真分析证实所提算法的合理性与有效性，能够提高配电网的经济效益。

[1] Z Merlin A, H. Back, search for a minimal-loss operating spanning tree configuration in an urban power distribution system, in Proc 5th power system computation Conf, Cambridge, U[Z]. 1975: 1-18.

[2] H. Cheng and C. C. Kou. Network reconfiguration in distribution system using simulated annealing, Elec Power Syst Res, 1994(29): 227-238.

[3] 黄弦超, 杨雨. 基于电流分点编码的遗传算法在配电网重构中的应用[J]. 电力系统自动化, 2013, 37(19): 74-79.

[4] 沈广, 陈允平, 刘栋. 基于最小生成树编码的配电网恢复遗传算法[J]. 电力系统自动化, 2007, 31(14): 81-84.

[5] 许立雄, 吕林, 刘俊勇. 基于改进粒子群优化算法的配电网络重构[J]. 电力系统自动化, 2006, 30(7): 27-30, 79.

[6] 李振坤, 陈星莺. 余坤等配电网混合粒子群算法[J].中国电机工程学报, 2008, 28(31): 35-41.

[7] Shi Y, R. C[C]//of the IEEE International Conference On Evolutionary Computation, 2001: 101-106.

[8] Rao R V, Savsani V J, Vakharia D P, Teachinglearning-based optimization: A novel method for constrained mechanical design optimization problems[J]. Comput Aided Design 2011, 43(3): 303-315. [9] Baran M E, Wu F F, Network reconfiguration in distribution systems for loss reduction and load balancing[J]. IEEE Trans Power Delivery 1989, 4(2): 1401-1407.

The Research for Dynamic Distribution Network Reconfiguration based on Hybrid Optimization Algorithm

Shi Huizhe1Liu Zhipeng2Zhong Wenqiang3
(1. Shandong University of Science and Technology, Qingdao, Shandong 266590; 2. Hainan State Grid Corporation Dispatch and Control Center, Haikou 570203; 3. State Grid Pingdu Power Supply Company, Pingdu, Shandong 266000)

The proposed approach presents a hybrid algorithm which combines the Chaotic Particle Swarm Optimization and Teaching-Learning Optimization to overcome the Distribution Network Reconfiguration problem. Establish the mathematical model that bases on the minimum cost of operating, the minimum of network loss and the least number of switching operations. Form the comprehensive index including network loss and voltage deviation by the normalized processing.Set the maximum standard deviation of it and the maximum number of system reconstruction, determine the reconstruction period. This approach combines the Chaotic Particle Swarm Optimization and Teaching-Learning Optimization to find the global optima in more efficient way.In order to tune the inertia weight factor dynamically in distribution network reconfiguration, a chaotic framework is introduced to the PSO algorithm. Meanwhile the hybrid algorithm which include Teaching-Learning Optimization can guarantee diversity, limit the initial population premature convergence and improve the ability of the algorithm optimization. Finally, to validate the effectiveness and reasonableness of the proposed algorithm it is applied to IEEE 33 systems.

distribution network reconfiguration; reconstruction period; chaotic particle swarm optimization; teaching-learning optimization

时慧喆（1990-），男，硕士研究生，主要从事配电网重构方面的研究。