基于冲击回波法识别无砟轨道混凝土结构中的蜂窝伤损深度研究

胡志鹏

(中铁第一勘察设计院集团有限公司，西安　710043)



基于冲击回波法识别无砟轨道混凝土结构中的蜂窝伤损深度研究

胡志鹏

(中铁第一勘察设计院集团有限公司，西安710043)

为了研究高速铁路无砟轨道混凝土结构相继出现不同程度的伤损问题，借助于有限元软件ANSYS LS-DYNA 3D数值模拟冲击回波，研究应力波在轨道板中的传播速度和传播规律，采用冲击回波法识别轨道板中蜂窝伤损的深度。研究结果表明: 应力波在蜂窝伤损和砂浆界面发生反射，在频谱图中形成不同峰值，通过频谱伤损定位原理可以确定出轨道板中蜂窝伤损的具体深度。

冲击回波法；蜂窝伤损；无砟轨道；高速铁路

1　概述

随着我国高速铁路的大量兴建，无砟轨道得到了快速发展与广泛应用。截止2015年年底，我国高速铁路运营里程约1.9万km。但在建设过程中，由于环境条件、技术缺陷及施工质量的影响，致使轨道板、道床板中出现蜂窝伤损[1]。这些伤损随着列车荷载的作用会逐渐恶化，进而影响列车的安全运营，准确识别出轨道板和道床板中的蜂窝伤损显得尤为重要。

目前，检测混凝土伤损的方法较多，但由于无砟轨道为不同材料层状结构，且轨道板中配置一定数量钢筋的影响，使得一些方法受到限制。冲击回波法是一项新的检测技术，该方法基于应力波反射法对伤损进行识别，在公路、桩基等混凝土结构伤损检测中应用较多，还未应用到无砟轨道伤损检测中来[2-4]。因此，本文探索将冲击回波法应用到无砟轨道伤损检测，利用有限元软件ANSYS LS-DYNA 3D模拟验证该方法在无砟轨道伤损检测中的可行性以及准确性[8-13]，以无砟轨道中混凝土蜂窝伤损为背景，识别无砟轨道中蜂窝伤损的深度。

2　理论背景

2.1冲击回波原理

冲击回波法是基于应力波在混凝土结构内部传播时，遇到不同波阻抗界面发生反射的原理。当用激励设备敲击无砟轨道板表面时，就会形成一个瞬时的应力波，当应力波在传播过程中遇到蜂窝、离缝，或CA砂浆、混凝土边界面时，由于两种界面的波阻抗存在差异，因此会在这些界面处发生反射。正是由于应力波在伤损或边界面处的不断反射，使得在结构物表面形成一个瞬时的类谐振条件，若将传感器放置于激励设备附近时，便可接收到应力波在多次反射下的振动信号[3-4]。再将时域信号经过信号处理转化为频域信号，根据频域值来反算伤损深度。其原理见图1。

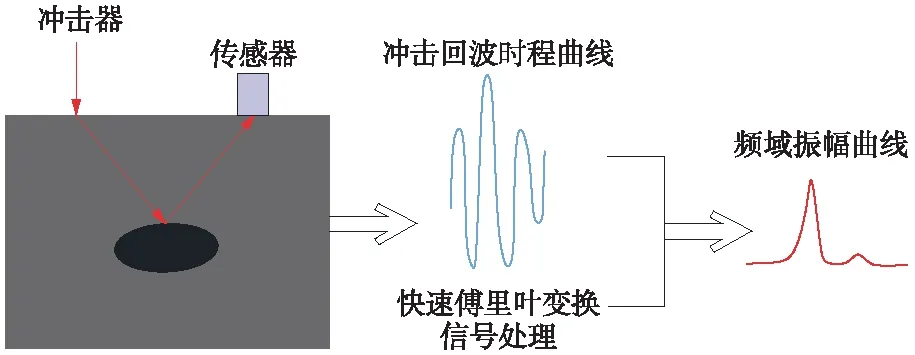
图1　冲击回波法原理示意

2.2频谱伤损定位原理

冲击回波法在早期是采用时域信号来识别损伤，通过记录结构物上应力波到达的时间差来确定伤损深度，由于时域信号因不同的操作和记录得出不同的结果，存在较大的误差，影响测试结果，因此这种时域方法有很大的局限性。随后，美国康奈尔大学Sansalone和Carino教授利用频域分析的方法来识别伤损，即将实际测得的时域信号转化为频域信号，提升了识别的精度，促进了该方法在无损检测中的应用并提高了检测精度[6-7]。

根据冲击回波法的原理，应力波在不同阻抗界面处或边界面处不断反射，形成瞬时的周期性振动，当放置于冲击点附件的传感器接受信号时，应力波在结构中已传播2D的距离，此处的D即为测试面与反射面之间的距离，又因为是瞬时周期性振动，所以传播频率可认为是时程的倒数。因此，可得到计算公式

(1)

式中，Cpp为应力波通过板厚度方向的波速；D为反射面到测试面的距离。

3　数值模拟

3.1模型建立

冲击回波法数值模拟中，为了简化计算，将非匀质混凝土轨道板结构视为各项同性的均匀结构。建立轨道板-砂浆-支承层有限元模型，为了计算时与实际情况相符，轨道板、CA砂浆和支承层都选用实体单元SOLID164进行建模，该单元是三维实体单元，具有8个节点，每个节点有9个自由度；该单元在默认情况下采用单点积分算法。由于研究内容涉及波的传播，建模时需进行边界条件处理，除了将支承层底部全约束外，还需考虑无反射边界条件，为避免边界处波的反射对求解域的影响，将轨道板和砂浆四周进行无反射处理。

轨道板、CA砂浆和支承层的建模参数如表1所示。

表1　无砟轨道材料参数

3.2加载

(1)激振力

为了模拟冲击回波，锤击轨道板的瞬态激振力可以采用半正弦脉冲来模拟，根据大量的测试研究结果，式(2)更接近于实测的力波，能够较理想地描述锤激力，根据现场试验数据，选择激振力持续作用时间为32 μs，在16 μs时载荷达到最大值。激振力垂直加载到与蜂窝伤损相对应的轨道板表面上。

(2)

(2)步长选取

基于应力波的传播来识别伤损深度，这就涉及到应力波的波动问题，因此积分时间步长Δt要保证应力波在单元之间传播时足以捕捉到波动效应。应力波在无砟轨道混凝土结构中以纵波形式传播，要能在计算中捕捉到这种波，则Δt应满足

(3)

3.3应力波在无砟轨道中的传播

(1)波速的确定

波速的确定可以通过2种方法来求取：

①从已知的构件厚度，通过频域计算反算出应力波在轨道板中的波速；

②通过提取两节点之间的应力时间差值反算出波速。

利用冲击回波原理定位轨道板中伤损深度时，首先得确定应力波在轨道板中的波速。因此，建立1块0.19 m厚的混凝土轨道板试件，在轨道板上施加瞬时冲击力，通过建立模型计算距敲击点0.04 m处响应点的结果，如图2所示。

从图2中可以看出，将速度-时程曲线经过傅里叶变换之后得到频谱图，两个峰值处所对应的频率分别为10.22、23.21 kHz，在20 kHz内第一个峰值为应力波纵波经混凝土—空气界面即波阻抗发生变化的界面处发生反射引起瞬时共振的结果，由于结构厚度已知，经反算得出应力波在轨道板中的传播速度为4 013 m/s，为了验证该波速的准确性，下面通过两节点之间的应力传播时间差来计算波速，计算结果如图3所示。

图2　时域和频域计算结果

图3　提取不同节点处的应力值

从图3可以看出，通过提取顶面和距顶面0.08 m处的应力值，两节点的应力时间差为1.99×10-5s，经计算得出应力传播速度为4 015 m/s，基本与频域确定出的波速一致，因此，将应力波波速取为4 015 m/s，为后续计算提供重要参数。

(2)应力波在轨道板中的传播规律

为了进一步探索应力波在无砟轨道中存在伤损时传播和反射的规律，建立了轨道板-CA砂浆-支承层结构，并在轨道板中设置一定尺寸的缺陷，轨道板尺寸为0.6 m×1.5 m×0.19 m，CA砂浆层和支承层长宽跟轨道板一致，CA砂浆和支承层厚度分别为0.03 m和0.1 m，伤损尺寸为0.2 m×0.1 m×0.03 m，蜂窝损伤离轨道板表面0.095 m。由于研究的重点是轨道板和砂浆中应力波的传播，故将支承层厚度取为0.1 m。

冲击荷载选用半正弦荷载，最大幅值为1 kN，冲击作用时间为32 μs。在轨道板上施加瞬时冲击荷载后，应力波会在轨道板内部传播，为了能直观的描述应力的变化过程，绘制了如图4所示的5个时间节点上的应力云图，通过这些不同时间点上的应力变化，进一步直观的描述应力波在无砟轨道结构中的传播规律。

图4　无砟轨道在冲击力作用下不同时刻应力云图

从图4可以看出，当在轨道板上某一节点处施加瞬时荷载后，应力会沿着轨道板横向和纵向传播。在70 μs时，应力波首次到达混凝土-空气边界面，可以看出此时一部分应力波在边界处发生发射，一部分继续沿垂向传播。在110 μs时，应力波垂向到达混凝土/CA砂浆界面处，从该时刻的应力云图中可以看出应力波在不同材质界面处发生反射，这也证实了应力波在遇到不同波阻抗介质时发生反射的结论。为了更详细地研究应力波在轨道板中的传播规律，分别提取伤损上部和伤损下部节点处的应力值，如图5所示。

图5　无砟轨道在瞬时力作用下不同时刻应力

图5为伤损垂向距轨道板不同距离节点处的应力值，从图中可以看出，在同一应力值处时间历程逐渐增加，说明了应力波中纵波沿轨道板纵向逐渐传递。从计算结果中还可以看出应力波在轨道板中传播时，应力随着深度的增加逐渐减小，尤其是经过伤损时应力的衰减更大。

图6和图7为伤损下部节点处的应力结果，从图中可以看出，在134 μs前应力为零，在之后才出现应力，说明应力绕过伤损后传播到伤损下部，并且应力的最大值只有20 Pa，随着深度的增加应力逐渐减小。

图6　1/4模型伤损下面节点应力云图

图7　伤损下面节点不同时刻应力

(3)轨道板板厚频率

由于无砟轨道系统中轨道板为板状结构，为了研究无砟轨道结构中不同厚度轨道板的板厚频率，分别建立了不同厚度的无砟轨道模型，其中轨道板厚度为0.05、0.10、0.15、0.20、0.25、0.30 m；CA砂浆和支承层厚度分别为0.03、0.10 m。通过计算拟合出轨道板板厚频率与厚度之间的关系，如图8所示。

图8　轨道板厚度频率随板厚的变化规律

从图8可以看出，通过对6个不同厚度的轨道板进行动力计算后，得出轨道板厚度频率随着厚度的增加而逐渐减小，但在我国实际的无砟轨道结构中轨道板的厚度为0.2 m左右，因此与其相对应的厚度频率为10 kHz。这说明当轨道板中存在伤损时，其伤损处的计算频率会大于10 kHz，这一条件为准确识别出伤损深度提供便利。

3.4轨道板中不同深度蜂窝伤损的识别

为了研究冲击回波法确定不同深度的蜂窝伤损，分别建立伤损距轨道板顶面0.095 m和0.13 m两种工况，见表2。计算结果如图9所示。

表2　轨道板中不同深度蜂窝伤损

图9　两种工况下频谱计算结果

从图9(a)频域图中可以看出，在20 kHz内出现两个明显的峰值，分别为18.6、13.6 kHz，还有两个频域峰值分别为7.55、9.96 kHz。由于应力波要绕过轨道板内部缺陷才能被底部边界面反射，使得传播路径增大，而应力波在蜂窝伤损处的反射路径较短。因此，在频谱图中结构厚度频率向低频部分移动，而伤损处频率则向高频漂移，这也是判断伤损的主要依据。

图9(b)中，18.6、13.6 kHz两处峰值所对应的深度分别为0.096、0.13 m，最大峰值18.6 kHz所对应的厚度为0.096 m，即为伤损深度，与预设伤损深度0.095 m一致。因为应力波在轨道板中传递过程中最先遇到波阻抗发生变化的伤损界面，应力波首先在混凝土-空气界面发生反射，使得敲击点附近最先发生共振，且共振频率最大。而13.6 kHz峰值处对应深度为0.13 m即伤损底面，应力波在空气-混凝土界面处发生反射。9.96 kHz峰值经计算所对应深度为0.192 m，该深度对应混凝土-砂浆界面。频域图中的峰值从大到小也分别反映出了应力波在不同波阻抗界面处发生的反射，通过最大频域峰值可以计算出伤损的具体深度。

图9(b)中，20 kHz内出现3个明显的峰值，分别为16.1、9.94、7.45 kHz。根据工况一计算得出的结论验证工况二伤损的深度，通过20kHz内的最大频率峰值16.1 kHz，反算得出伤损深度0.128 m。与伤损深度基本一致。从以上两种工况的计算结果中可以看出冲击回波法能准确的检测出轨道板中不同深度的蜂窝伤损。

4　结论

通过数值模拟冲击回波检测无砟轨道混凝土结构中的蜂窝伤损，可以得出以下结论。

(1)应力波中纵波沿轨道板纵向逐渐传递，且在轨道板中传播时发生衰减现象。

(2)轨道板板厚频率随着厚度的增加而逐渐减小。

(3)应力波在蜂窝和混凝土-砂浆界面均发生反射，由于蜂窝在轨道板中，所以在频谱图中出现的峰值较轨道板-CA砂浆界面处大。

(4)冲击回波法可以准确的识别出板式轨道中不同深度的蜂窝伤损。

[1]魏祥龙，张智慧.高速铁路无砟轨道主要病害(缺陷)分析与无损检测[J].铁道标准设计，2011(3):38-40.

[2]姚华.扫描式冲击回波法检测后张预应力管道内缺陷的模型试验研究[D].成都:西南交通大学，2008:9-15.

[3]傅翔，宋人心，王五平，等.冲击回波法检测预应力预留孔灌浆质量[J].施工技术，2003，32(11):37-38.

[4]罗骐先，傅翔，宋人心，等.检测混凝土内部缺陷与厚度的冲击反射法及测试系统[J].公路，2001，3(3)：56-60.

[5]刘学毅，赵坪锐，杨荣山，等.客运专线无砟轨道设计理论与方法[M].成都：西南交通大学出版社，2010:56-85.

[6]Lin Yiching，Mary Sansalone，Nicholas J.Carino，Finite Element Studies of the Impact-Echo Response of Plates Containing Thin Layers and Voids[J].Journal of Nondestructive Evaluation，1990，9(1):28-35.

[7]Sansalone M，Carino N J.Finite Element Studies of the Impact-Echo Response of Layered Plates Containing Flaws[J].International Advances in Nondestructive Testing，1990(2):313-336.

[8]郭弦.冲击作用下混凝土中应力波传播规律研究[D].长沙:国防科学技术大学，2010:35-45.

[9]伍允望.应力波反射法数值模拟分析及实践研究[D].上海:同济大学，2007:9-14.

[10]王致富.低应变反射波法振源特性仿真分析[D].成都:西南交通大学，2010:15-22.

[11]潘冬子，章光，马宝斌，等.应力波反射法测混凝土桩完整性的数值模拟及实验研究[J].公路交通科技，2004：64-69.

[12]Liu P，Yeh P.Vertical spectral tomography of concrete structures based on impact echo depth spectra[J].NDT & E International，2010，43(1):45-53.

[13]李杰.基于应力波反演的管道损伤识别技术研究[D].北京:中国石油大学，2008：18-33.

Identify the Depth of Honeycomb in Ballastless Track Concrete Structure Based on Impact-echo Method

HU Zhi-peng

(China Railway First Survey and Design Institute Group Co.，Ltd.，Xi’an 710043，China)

To study the different degrees of damages in ballastless track concrete structure encountered in the operation of railway ballastless track，this paper uses the finite element software ANSYS LS-DYNA3D to simulate the impact-echo and learn the propagation speed and rules of the stress wave in the track slab，and employs the impact-echo method to identify the depth of damage in the track slab.The results show that the stress waves reflect on honeycomb and mortar interface and generate different peak values in frequency spectrum graph，and the specific depth of honeycomb can be calculated according to the principle of frequency spectrum to locate damages.

Impact-echo method; Honeycomb damage; Ballastless track; High-speed railway

2016-01-26；

2016-04-01

四川省科技支撑计划项目(2012GZ0104)

胡志鹏(1990—)，男，助理工程师，E-mail：zpenghu@163.com。

1004-2954(2016)10-0022-05

U214.1+8

A

10.13238/j.issn.1004-2954.2016.10.006