快速傅立叶变换FFT算法特点分析

徐美清+孙晨亮

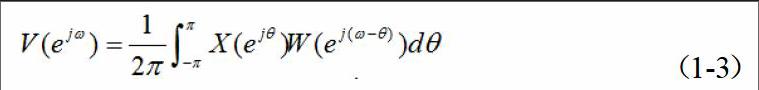
摘 要：快速傅立叶变换FFT是离散傅立叶变换DFT的一种快速算法，计算量小的显著的优点，使得FFT在现代数字信号处理与数据分析领域获得了广泛的应用。但是在利用FFT算法对连续信号进行分析时，存在频谱混叠、栅栏效应及频谱泄露现象。本文简单介绍了FFT算法，并对其存在的缺点进行了详细的分析。

关键词：傅立叶变换；频谱混叠；栅栏效应；频谱泄露

1 FFT简介

快速傅里叶变换（Fast Fourier Transform，简称为FFT）并不是一种新的变换， 而是离散傅里叶变换（Discrete Fourier Transform，简称为DFT）的一种快速算法。在相当长的时间里，由于DFT的计算量太大，即使采用计算机也很难对问题进行实时处理，所以并没有得到真正的运用。直到1965年J.W.Cooley和J.W.Tukey首次提出了DFT运算的一种快速算法，后来又有G.Sande和J.W.Tukey的快速算法相继出现以后，情况才发生了根本的变化。人们开始认识到DFT运算的一些内在规律，从而很快地发展和完善了一套高速有效的运算方法，这就是现在人们普遍称之为快速傅里叶变换FFT的算法。

2 FFT算法的优点

FFT算法使DFT的运算大大简化，使其运算速度提高了1-2个数量级，从而使DFT的运算在实际中真正得到了广泛的应用。

3 FFT算法的缺点

利用FFT对连续信号进行傅里叶分析时可能造成一定的误差，从而产生频谱混叠、频谱泄漏以及栅栏效应现象。

3.1 频谱混叠

对连续信号进行采样时，通常假定所处理的信号是带限的。假设连续信号的最高频率为fh，采样频率为fs，那么根据香农定理，为了不产生混叠现象，应该有

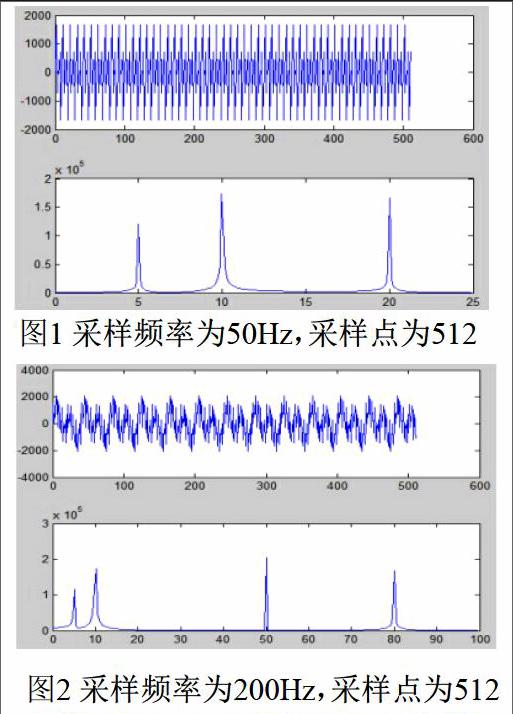
如果不满足fs≥2fh，就会产生频谱的交叠，即频谱混叠，从而产生失真现象。下面对频谱混叠现象进行举例说明，假定连续信号具有4个频率（5Hz，10Hz，50Hz，80Hz）分量，其采样点数为512个，采样频率fs为分别取50Hz和200Hz，用FFT对它进行频谱分析，其频谱图如下。

通过频谱图，我们可以看出采样频率对频谱的影响，当采样频率为50Hz时并不能分析出原信号中含有的信号，当采样频率为200Hz时没有发生混叠，能准确的分析出原信号中的频率分量。但在此需注意两个问题：第一，对采样定理中“两倍”含义的理解，容易产生如下的误解：“如果采用采样频率fs对一个信号进行采样，信号中fs/2以上的信息会消失”，采样定理的证明过程显示当采用采样频率fs对一个信号进行采样，信号中fs/2以上的信息不是消失，而是对称的映像到fs/2以下的频带中，并且和fs/2以下原有的频率成分叠加起来，从而产生混叠；第二，上述信号是假定带限的信号，如果连续信号是非带限的，那么将无法准确的从有限的采样点中分析原始信号的频谱，而只能通过适当提高采样频率和增加采样点来减少对频谱分析所造成的影响。

3.2 栅栏效应

利用FFT计算频谱，只给出离散点 或 上的频谱取样值，也就是只给出了基频的整数倍的频谱值，而不可能得到连续频谱函数， 这就像通过一个“栅栏”观看信号频谱，所以只能在离散点上看到信号频谱， 这种现象称之为“栅栏效应”。减小栅栏效应的一个方法就是要使频域取样更密，即增加频域取样点数N，在不改变时域数据的情况下，必然是在数据末端添加一些零值点，使一个周期内的点数增加，但并不改变原有的记录数据。频谱取样为 ，的增加必然使样点间距更近（单位圆上样点更多），谱线更密，谱线变密后原来看不到的谱分量就有可能看到了。

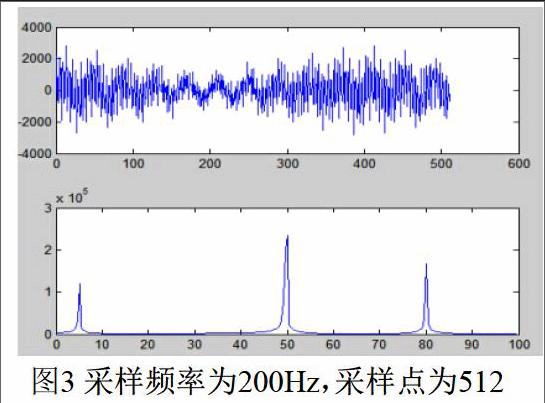
为更好地说明FFT计算频谱时存在的问题，对分析对象进行一些改动，令f2=49.5Hz，其他频率成分不变，采样频率fs=200Hz，利用Matlab可得其信号和频谱图如图3所示。

虽然采样的频率合适了，但是信号的频率分辨率还是比较低的，并没能反应出频率为49.5Hz的信号，这就是栅栏效应的结果。

3.3 频谱泄漏

对信号进行FFT计算，首先必须使其变成有限时宽的信号，这就相当于信号在时域乘一个窗函数如矩形窗，窗内数据并不改变。时域相乘即v（n）=x（n）·w（n），加窗对频域的影响，可用下面的卷积公式表示

卷积的结果，造成所得到的频谱V（ejω）与原来的频谱X（ejω）不相同，有失真。这种失真最主要的是造成频谱的“扩散”（拖尾、 变宽），这就是所谓的“频谱泄漏”。

我们利用SPTOOL工具箱的频谱分析功能，通过改变窗的类型，分析窗对减小能量泄露的影响。采用WELCH方法，其中采样频率Fs=200Hz，FFT采样点（Nfft）=512，Nwind=256。分别对信号加矩形窗（boxcar）、三角窗（triang）、汉宁窗（hanning）、汉明窗（hamming）和布莱克曼窗（blackman）后频谱图如图4至图6所示。

从这些加窗后的频谱图分析比较可以看出，矩形窗的频谱的主瓣比较小，但是它对旁瓣的抑制却是比较差的；三角窗对旁瓣抑制比较好，但代价是牺牲了主瓣，它的主瓣比矩形窗的主瓣宽度增加不少；汉宁窗使能量集中在主瓣，旁瓣大大减小，主瓣宽度比矩形窗的主瓣宽度增加一倍左右。

各个频谱图上都看不到频率为49.5Hz的信号，这说明各种窗的加入还是对频率分辨率有比较大的影响，泄漏造成的后果是降低频谱的分辨率。此外，由于在主谱线两边

形成很多旁瓣，引起不同频率分量间的干扰（简称谱间干扰）， 特别是强信号谱的旁瓣可能湮没弱信号的主谱线，或者把强信号谱的旁瓣误认为是另一信号的谱线，从而造成假信号，这样就会使谱分析产生较大偏差。所以对于窗函数的选择需要在主瓣宽度、第一旁瓣水平和旁瓣水平大小随频率增加而降低的速度之间进行折中选择。

参考文献

[1]程佩青.数字信号处理教程[M].清华大学出版社，2001.

[2]胡广书.数字信号处理理论、算法与实现[M].清华大学出版社，2004.

[3]丁玉美，高西全.数字信号处理[M].西安电子科技大学出版社，2001.

[4]潘士先.谱估计和自适应滤波[M].北京航天航空大学出版社， 1991.