基于自抗扰控制技术的船舶航向自动舵控制方法研究

2016-10-14黄志坚

船电技术 2016年11期

刘晓，黄志坚，张赞

刘晓，黄志坚，张赞

(上海海事大学，上海 201306)

本文基于线性Nomoto船舶运动模型，以传统PID控制器为基础，考虑到船舶自身状态和外界未知干扰对船舶航向系统的影响，对船舶航向自动舵控制系统引入自抗扰技术，建立以自抗扰控制方法为基础的船舶航向控制系统。最后利用Simulink仿真软件搭建系统的仿真模块，对改进的船舶航向控制系统的性能进行仿真验证。结果表明该方法具有较强鲁棒性、抗干扰性，解决了超调性与快速性之间的矛盾。在应对海上复杂的环境时有良好的动态性能和稳态性能。

船舶自动舵自抗扰控制器传统PID控制 Simulink

0 引言

船舶在航行时会受到自身状态和外界不确定因素如风、浪、流等的影响，这些未知扰动对船舶航向自动舵的控制性能提出了很高的要求。目前船舶航向自动舵的控制器主要应用PID 控制方法，PID控制方法的原理是根据系统的输出信号和输入信号的误差及其微分、积分的线性组合来产生控制信号[1]。由于船舶自动舵系统的强耦合性和航行环境的不确定性等因素，在给出控制信号后，控制器产生反应到船舶自动舵的开始运动之间会产生时间延迟，使得传统PID控制器出现了超调性和快速性之间的矛盾。这些问题的存在使其不能很好的适应船舶航向的控制。

本文的主要目的是基于线性 Nomoto 船舶运动模型[2]，对船舶航向自动舵控制系统提出一种基于自抗扰技术的控制方法。该方法充分吸收PID控制方法的思想“基于误差消除误差”，加入特殊的非线性效应。从而产生了以下两个重要优点：1）有效解决了快速性和超调性之间的矛盾，提高了控制精度；2）应用范围广，具有一定的自适应性和鲁棒性。

1 传统PID自动舵数学模型[3]

在早期传统PID控制器中舵角的控制方程为

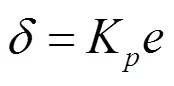
式中：是航向偏差信号；是比例系数。为避免控制效果产生振荡，的取值尽量要小。

比例控制在船舶低速稳定航行时控制效果基本上能够满足船舶航行的控制需求。但对于不稳定航行的船舶，只有比例控制是不够的，应加入航向偏差的微分项。控制方程为

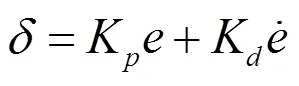
式中：K为控制器的积分系数。由于海上航行环境恶劣复杂，外界未知扰动会使得自动舵偏离期望的设定值而产生静态误差，为保持船舶沿着设定航向角航行，还要加入航向偏差的积分项。控制方程为

(3)

式中：K控制器的微分系数。

控制参数KKK通过PID整定方法进行整定，整定好后能够使自动舵保持较好的操纵性。PID控制器的参数确定后在控制过程中保持不变。当船舶的动态特性或外界条件发生变化时，PID控制器不能同时跟踪设定航向角和消除外界扰动，控制效果不能达到预期。

本文采用的是日本学者野本谦作教授提出的线性船舶操纵数学模型，即著名的Nomoto模型，其数学模型为

式中，表示船舶航向角，表示舵角，为系统参数。传统PID船舶自动舵系统结构如图1所示。

2 自抗扰控制器（ADRC）

自抗扰控制技术（ADRC）是由韩京清教授首次提出的一种非线性控制技术，这种技术能够根据未知的非线性复杂系统模型，只根系统的输入和输出信息，对系统的未知扰动进行实时补偿和估计。自抗扰控制具有优良的控制效果及抗干扰能力。以自抗扰控制器的对象为二阶次，则其整体结构图如图2所示：

1）跟踪微分器（TD）。输入信号为设定值()，TD根据输入信号以及受控对象的特性安排过渡过程，输出信号为输入信号跟踪值及其微分信号。TD可以解决系统快速性和超调性之间的矛盾。TD常用形式为

(5)

式中：()表示输入信号；表示积分步长；(V，V，，)表示非线性函数。TD的正定参数为、。

2）扩张状态观测器(ESO)。ESO作为自抗扰控制器的主要部分，它不仅能估计系统的各个状态量，而且能够实时估计模型内部和外部扰动的作用值并在反馈中给出控制量对总扰动进行补偿。ESO 一般形式为

式中：()表示非线性函数；表示控制量，表示常系数；1，2表示信号y的状态估计量;3表示总干扰估计信号。ESO的正定参数为{α，α，β，β，β，δ}。

3) 非线性状态误差反馈规律

(NLSEF)NLSEF给出被控对象的控制策略。它是跟踪微分器（TD）的输出状态量和扩张状态观测器（ESO）产生的状态变量估计之间的误差的非线性组合，NLSEF 一般形式为:

NLSEF的整定参数为{ααββδ}。

自抗扰控制器的参数一经整定，参数的变化对控制效果的影响不大，因此比较容易的得出自抗扰控制器的参数。

3 基于自抗扰技术的自动舵控制

本文将自抗扰技术引入船舶航向自动舵中的控制器部分，用一种基于自抗扰技术的控制器代替传统的PID控制器，其系统结构如图3所示：TD用于跟踪船舶航向角设定的值及其微分信号；ESO的作用是根据舵角δ和实际航向,对船舶航行自身状态和未知扰动总和进行跟踪估计；NLSEF为TD的输出值和ESO产生的状态变量估计之间误差的非线性组合，根据未知扰动的估计信号可得出控制量进行扰动补偿。

4 基于Simulink的仿真

利用MATLAB/Simulink仿真软件，建立基于自抗扰技术的船舶航向自动舵系统的仿真模型。对所提出的船舶航向自动舵的控制性能进行仿真验证。

本文采用大连海事大学“育龙”实习船为例进行仿真研究，船舶具体参数为：柱间长126 m，船宽21.8 m，满载吃水8.0 m，方形系数0.681，船舶初始速度为7.2 m/s，根据已知参数，计算得=261.73，=0.42。则线性Nomoto船舶运动模型可以表示为

在传统PID控制参数中，取=0.06，=0.9。根据传统PID船舶航向自动舵的参数整定方法，PID设计参数为=2.2434，=0.0135，=64.9210。自抗扰整定参数为TD的=0.004，=0.01； ESO 的{0.01，0.01，100，200，500，0.01，0.01}；NLSEF 的{1.75，0.25，50，20，0.01}。图3为船舶低速稳定航行，设定外界条件为没有风浪干扰，当设定航向为10°时，船舶航向跟随时间的变化曲线，图中虚线为传统PID控制器的仿真结果。从图3中可以看出，自抗扰控制器的变化曲线超调量小，响应速度快，达到给定航向的时间与PID控制器相比大大缩短，一定程度上解决了PID控制器存在的快速性与超调性之间的矛盾。

图4为舵角的变化，仿真结果表明，基于自抗扰技术的自动舵航向误差最后也是趋于零，说明基于自抗扰技术设计的控制器具有较好鲁棒性。

5 结论

本文首先介绍了传统PID航向自动舵的数学模型，以线性Nomoto船舶运动模型为基础，考虑到船舶自身和外界环境引起的未知扰动，提出了用自抗扰控制器替代传统PID控制器。从MATLAB/Simulink软件的仿真结果得出了以下结论：基于自抗扰技术的航向控制系统在保证快速性的同时一定程度上抑制了系统的超调性；同时在恶劣海况下表现出较好的鲁棒性和自适应性，应用范围广泛。