基于帕累托最优的雷达-通信共享孔径研究

2016-10-14石长安刘一民王希勤

电子与信息学报 2016年9期

石长安刘一民王希勤于鹏

基于帕累托最优的雷达-通信共享孔径研究

石长安①②刘一民*①王希勤①于鹏②

①(清华大学电子工程系北京 100084)②(中国洛阳电子装备试验中心洛阳 471003)

针对雷达-通信综合射频系统，该文提出一种基于环境信息的共享孔径动态分配方法。首先基于帕累托最优理论将共享孔径分配建模为一个多目标优化问题，并建立了雷达阵列方向图的峰值旁瓣电平和多输入多输出(MIMO)通信系统的信道容量两个优化目标函数。然后提出一种基于整数编码的改进粒子群算法，通过迭代求解以帕累托前沿的形式给出一组最优解，供决策者根据任务需求从中选出一个最满意的解。最后，仿真结果验证了该方法的有效性。

共享孔径；综合射频系统；多目标优化；粒子群算法；帕累托最优

1 引言

为了适应信息化战争对作战平台多任务、多功能的需求，现代飞机、舰艇装备的雷达、通信、电子战设备越来越多，所占的体积、重量、功耗和成本也日益扩大，甚至造成了严重的电磁干扰。因此，利用综合孔径实现雷达、通信、电子战等多功能集成的综合射频系统已经成为电子信息系统发展的重要方向，引起了世界各国的高度重视。工程实践表明，综合射频系统在一个共用的射频孔径上同时实现雷达、通信、电子战等功能，可以改善作战平台的电磁兼容性和隐身性能，从而提升武器系统的整体作战效能。自20世纪80年代起，美国通过持续不断地研究取得了令人瞩目的成绩。美国空军相继开展了“宝石柱”(Pave Pillar)计划、“宝石台”(Pave Pale)计划等，逐步将多功能一体化向纵深方向推进；美国海军先后开展了先进共用孔径(ASAP)项目、先进多功能射频概念(AMRFC)项目、集成上层建筑(InTop)项目等，主要致力于孔径综合方面的研究，以解决天线数量增加带来的电磁干扰严重、装备隐身性差、维护保养困难等问题；美国国防部高级研究计划局(DARPA)开展了可重构孔径(RECAP)项目，重点研究通过微电子机械系统(MEMS)技术对天线进行重构。此外，欧洲防务局(EDA)开展的可扩展多功能射频系统(SMRF)项目，意大利与瑞典联合开展的多功能有源电子扫描阵天线(M-AESA)项目等也都取得良好的成绩。

在美国海军的AMRFC演示验证系统中，发射阵面被划分为4个相同的子阵，用于同时实现雷达、通信、电子战等功能[1]。这种固定的阵面划分方式缺乏足够的灵活性，不能随着任务需求或环境信息的变化而动态调整资源的分配状态。鉴于目前尚未发现共享孔径动态分配方面的公开文献，本文拟从雷达-通信综合射频系统入手，深入探讨基于环境信息的共享孔径动态分配方法。后续内容安排如下：第2节建立了共享孔径分配的多目标优化模型，给出了雷达阵列和通信阵列优化的目标函数，第3节介绍了帕累托最优的相关概念，提出了基于整数编码的改进粒子群算法，第4节给出了几种典型的仿真实验及结果分析，最后一节总结了本文的研究工作，并指出了下一步的研究方向。

2 共享孔径分配的多目标优化模型

相对于有源相控阵体制，数字阵列体制利用数字方式对天线各阵元独立地进行发射/接收控制，不仅阵面划分灵活，而且每个子阵的波束指向、形状、频率和功率可以单独控制，是现阶段实现综合射频系统的最佳技术体制。因此，本文以1维数字阵列为例，研究雷达-通信共享孔径动态分配方法。

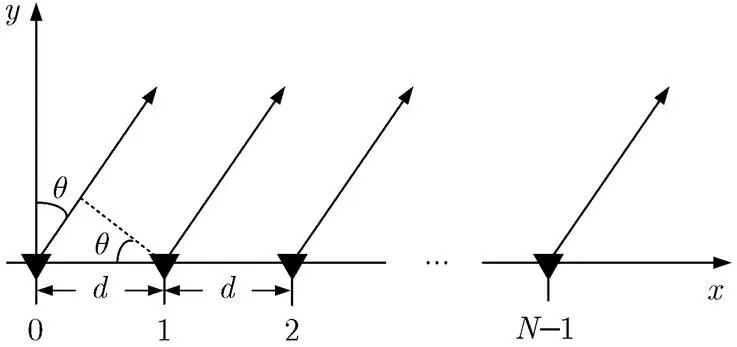
图1 均匀线阵示意图

由天线理论可知，阵列天线的辐射场是各阵元辐射场的矢量和。假定均匀线阵采用无方向性阵元，其阵列方向图可表示为

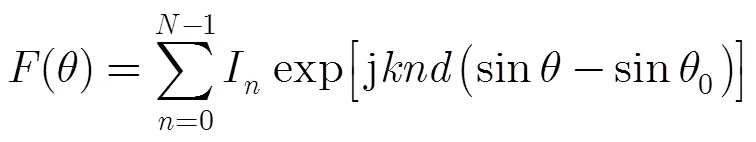
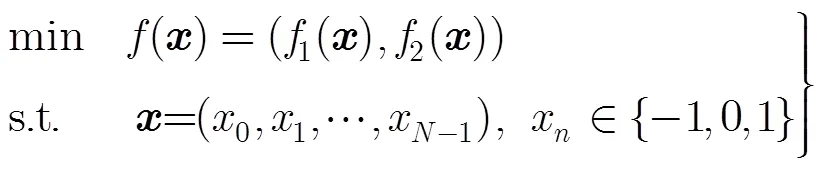
共享孔径分配的目的是通过调整各阵元的使用状态，使得雷达阵列和通信阵列同时获得良好的性能。

2.1雷达阵列优化的目标函数

对于雷达系统来说，共享孔径分配相当于附加了通信阵列约束的稀疏阵列优化问题。研究表明，与相同孔径的周期阵列(标准满阵，阵元间距为波长的一半)相比，稀疏阵列方向图的主瓣宽度基本不变，但是旁瓣电平会剧烈起伏。因此，在稀疏阵列优化问题中，人们通常采用峰值旁瓣电平作为优化目标函数。

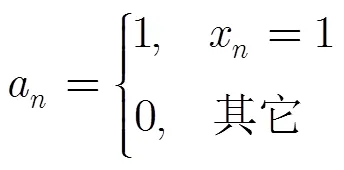
(4)

阵列方向图的峰值旁瓣电平(Peak Side-Lobe Level, PSLL)可表示为

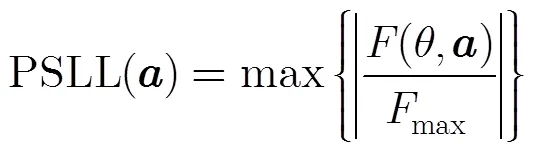
综上，雷达阵列优化的目标函数取为

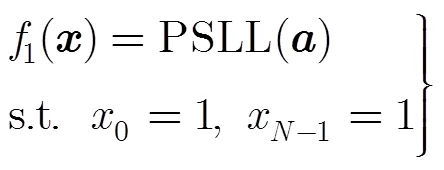
为了保持雷达阵列的孔径不变，在本文后续的理论分析及仿真实验中，图1所示阵列的最左和最右两个阵元始终分配给雷达使用，即。

2.2 通信阵列优化的目标函数

与单天线收发通信系统相比，MIMO(Multiple Input Multiple Output)通信系统在不增加带宽和天线总发射功率的情况下，可以极大地提高系统的信道容量[10,11]。假定MIMO系统有个发射天线，个接收天线，其信道矩阵可表示为

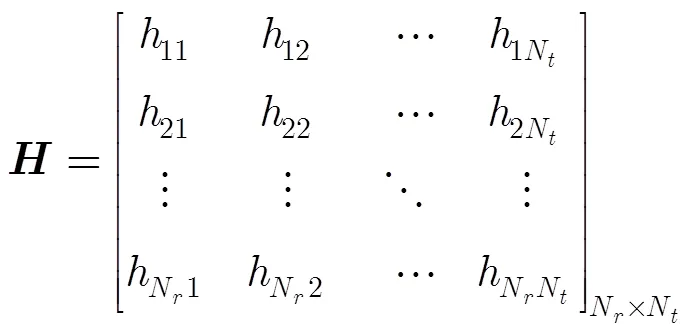
MIMO信道容量可表示为[11]

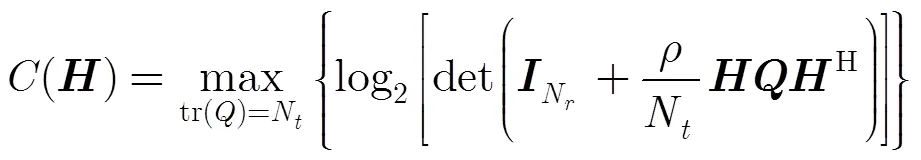
当发射端天线采用均匀功率分配方式时，信道容量可简化为[10]

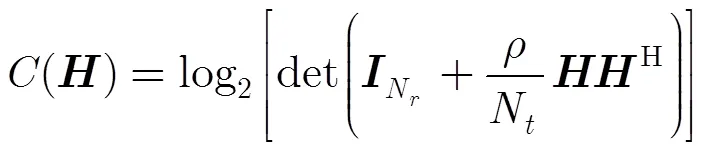
研究表明，当信道存在相关性时，MIMO信道容量将急剧下降。人们对相关信道模型的研究已经趋于成熟。不失一般性，假定相关信道采用Kronecker相关模型[12]，信道矩阵可表示为

(10)

在实际环境中，天线间隔是影响信道相关性的主要因素之一。天线间隔越小，相关性越大；天线间隔越大，相关性越小。根据这一特点，有人提出了单参数的指数相关模型[13]，相关矩阵的元素取值为

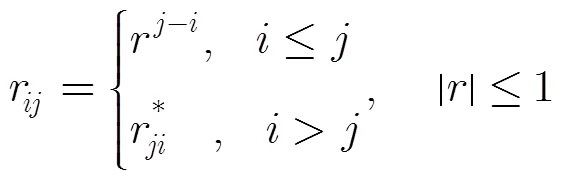
对于通信系统来说，共享孔径分配相当于附加了雷达阵列约束的天线选择问题[14,15]。不失一般性，这里采用最大化信道容量准则，即从个发射天线中选出个，也就是从中选出列构成新的信道矩阵，使得信道容量最大[15]。

为了便于写成最小化问题，通信阵列优化的目标函数取为

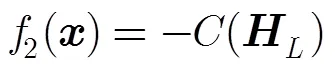
3 共享孔径分配的算法设计

与单目标优化问题不同，多目标优化问题的各个目标没有共同的度量标准，而且可能相互冲突，即一个目标的改善会以其它目标的恶化为代价，从而导致不存在使所有目标同时达到最优的全局最优解。换句话说，当存在多个优化目标时，“最优解”的概念产生了变化。本文以帕累托最优作为衡量资源分配优劣的标准，来协调处理两个不兼容目标的联合优化问题。

3.1帕累托最优理论

帕累托最优(Pareto Optimality)是博弈论中的重要概念。如果改变资源分配状态，在不使任何目标变坏的前提下，可以使至少一个目标得到改善，称为帕累托改进。帕累托最优是指没有帕累托改进余地的资源分配状态，即在不使其他目标变坏的情况下，不可能再使任何一个目标变好。

为了评价多目标问题解的优劣性，通常会用到以下几个定义[16]：

(1)帕累托支配关系(Pareto dominance relations)。对于任意两个决策矢量,(支配)，当且仅当

(2)帕累托最优解(Pareto optimal solutions)。决策矢量称为帕累托最优解，当且仅当

(14)

帕累托最优解又称为帕累托非支配解。

(3)帕累托最优集(Pareto optimal set)。所有帕累托最优解的集合称为该问题的帕累托最优集。

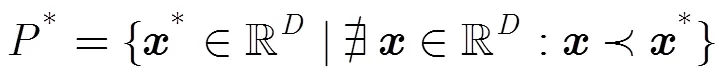
(4)帕累托前沿(Pareto front)。所有帕累托最优解对应的目标向量集合称为该问题的帕累托前沿。

(16)

多目标优化问题一般不存在唯一的最优解，而是存在一个帕累托最优集。求解多目标优化问题就是设法寻找尽可能多的帕累托最优解，并尽量使这些解在帕累托前沿上分布均匀。在实际应用中，根据对问题的了解程度和个人偏好，决策者可以从帕累托最优集中选出一个最满意的解。

3.2改进粒子群算法

本文的共享孔径分配是一个组合优化问题，难以获得解析解。粒子群优化算法(Particle swarm optimization)是一种基于群体智能的启发式搜索算法，在解决大规模复杂优化问题、空间函数寻优、动态目标寻优等方面得到了广泛应用。本文在借鉴PAES[21], SPEA2[22,23], NSGA-II[24,25]等算法的基础上，提出了一种基于整数编码的改进粒子群算法。该算法采用了基于拥挤距离的选择算子[17]、非支配解排序[24]、精英保留以及变异操作等多种策略，不需要准确衡量各优化目标之间的权重关系，而且可以同时处理一组最优解。

在粒子群算法中，每个个体称为一个“粒子”，代表一个潜在的可行解。在一个维的目标搜索空间中，设粒子群规模为，第个粒子的当前位置为，飞行速度为，该粒子迄今为止搜索到的最优位置为，整个粒子群迄今为止搜索到的最优位置为,。

在迭代过程中，粒子根据式(17)和式(18)进行速度和位置更新。

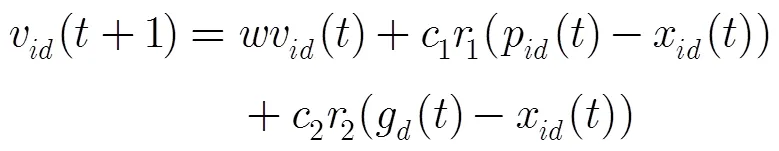
在共享孔径分配问题中，由于粒子位置为整数变量，故将位置更新公式修改为

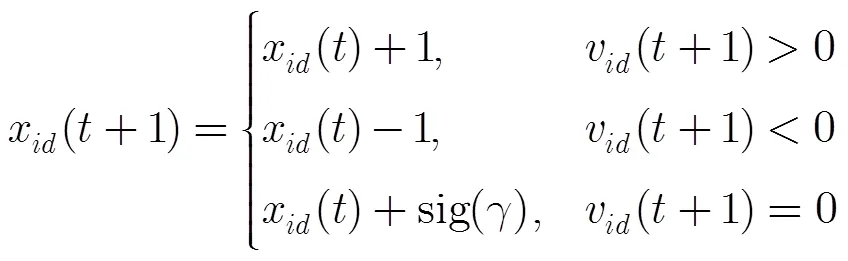
(20)

在进行速度更新时，改进算法采用可变的惯性因子，迭代公式为

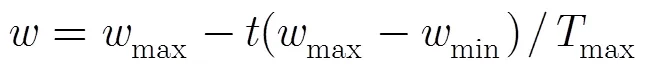
为了避免陷入局部最优，按式(17)完成位置更新之后，改进算法会以很小的变异概率从该粒子中随机选出1维按式(20)进行赋值，用来实现变异操作。

除了速度更新和位置更新，改进算法还包括以下3种更新：

(1)外部集更新。从当前群体中找出所有的帕累托最优解，按照帕累托支配关系对外部集进行更新。如果外部集已满，则删除最拥挤的粒子，让新粒子进入，这样既不损失最优解，又能给群体带来多样性。

(2)个体最优更新。从粒子的当前位置和历史最优位置中选择较优者，作为当前的个体最优，若两者无支配关系，则随机选择一个作为当前的个体最优。

(3)全局最优更新。计算当前外部集中各粒子的拥挤距离，然后从拥挤距离排名靠前的粒子(如前10%)中依次通过随机抽取为当前群体中的各粒子指定其全局最优。个体的拥挤距离越大，说明其所处的区域越稀疏，在进化过程中越应该被保留，这样优化出的帕累托前沿在分布上会更加均匀。

迭代结束后，最终的外部集就是帕累托最优集，该集合中所有元素对应的适应度值，共同构成了目标函数空间中的帕累托前沿。

图2为改进粒子群算法的流程图。

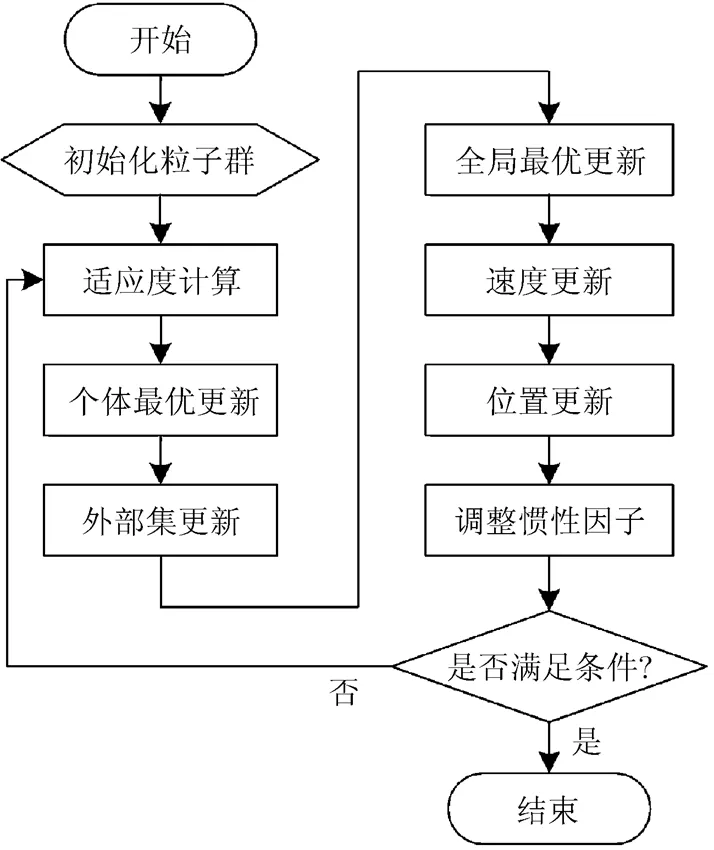
图2 改进粒子群算法的流程图

4 仿真实验及结果分析

本文研究共享孔径动态分配主要出于两种考虑：一种是环境信息(信道状态信息)改变了，要想获得期望的信道容量，需要优化调整各阵元的分配状态；另一种是环境信息基本未变(一般来说，信道状态不会一成不变，只是变化快与慢的区别)，但任务需求(对雷达性能和通信性能的重视程度)改变了，也需要优化调整各阵元的分配状态。

下面通过计算机仿真验证本文所提方法的有效性。共享阵列的参数：均匀线阵，阵元数，阵元间距，波长；假定通信系统发射天线相关，给定天线相关系数，由式(11)可得到发射相关矩阵；假定接收天线不相关，即接收相关矩阵，且接收端阵元数，接收信噪比。粒子群算法的参数：群体规模，最大迭代次数，惯性因子,，学习因子，外部集的规模。

图3给出了两种环境信息下的共享孔径动态分配问题的帕累托前沿，其中图3(a)的发射天线相关系数，图3(b)的发射天线相关系数。图中蓝色曲线上的“*”点为帕累托最优解，其他区域的“.”点为优化算法搜索过的所有可行解。帕累托最优解仅仅是可以接受的“不坏”的解，彼此之间并没有优劣之别，它们共同构成的帕累托前沿刻画出了在各种可能的资源分配状态下系统所能达到的性能边界。

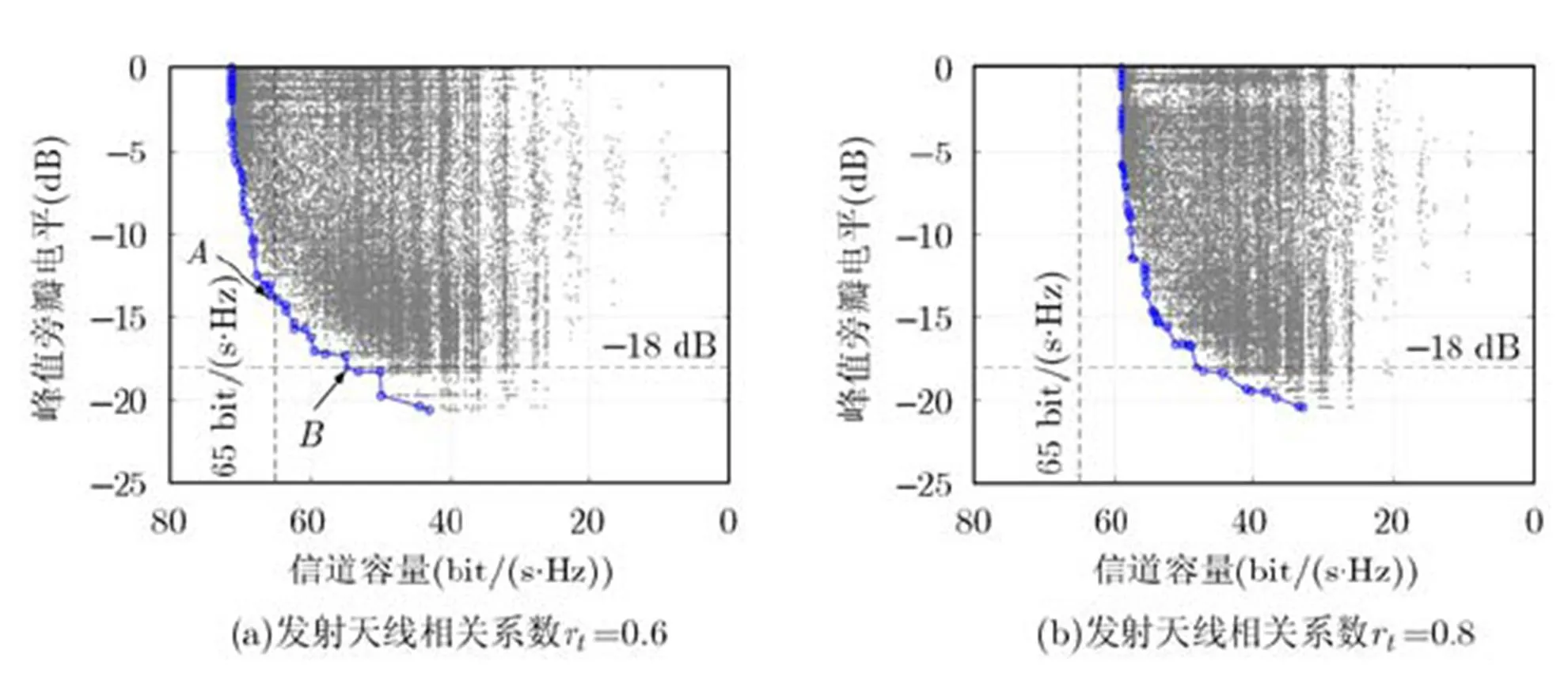
图3 两种环境信息下共享孔径分配问题的帕累托前沿

对比图3(a)和图3(b)可以看出，信道相关性的改变对信道容量的影响非常大。在第2种环境下，无论如何分配阵列资源都无法达到那条线。从理论上来说，雷达性能指标(方向图的峰值旁瓣电平)不受信道状态信息的影响，仿真结果也证明了这一点。图3(a)和图3(b)所能达到的最优旁瓣电平之所以存在细微差别，是因为智能优化算法无法保证每次寻找到的最优解完全一样。总之，当环境信息发生变化时，必须相应地调整各阵元的分配状态，才能实现共享孔径资源的最佳利用。

从图3还可以看出，无论在哪种环境信息下，雷达阵列和通信阵列都无法同时达到最优性能。在实际应用中，决策者可以根据对雷达性能和通信性能的不同重视程度，从帕累托前沿上选出一个最满意的解。以图3(a)为例，如果更加重视通信性能，比如要求信道容量优于，可以选择点作为最满意的解；如果更加重视雷达性能，比如要求峰值旁瓣电平优于，可以选择点作为最满意的解。点和点分别对应不同的阵列分配方案，各方案中所有阵元的分配状态如表1所示。

表1两种不同的阵列分配方案

图4给出了上述分配方案A和B所对应的雷达阵列方向图与相同孔径的周期阵列(标准满阵)方向图的对比情况，这3种阵列均未进行阵元幅度加权。可以看出，与周期阵列的峰值旁瓣电平相比，方案A由于偏重通信性能，其峰值旁瓣电平仅与周期阵列相当；方案B由于偏重雷达性能，其峰值旁瓣电平比周期阵列改善了约4.8 dB。在雷达阵列的阵元位置确定之后，如果采用阵元幅度加权进行优化，可以进一步降低其旁瓣电平，这表明该动态分配方法具有一定的实际应用价值。

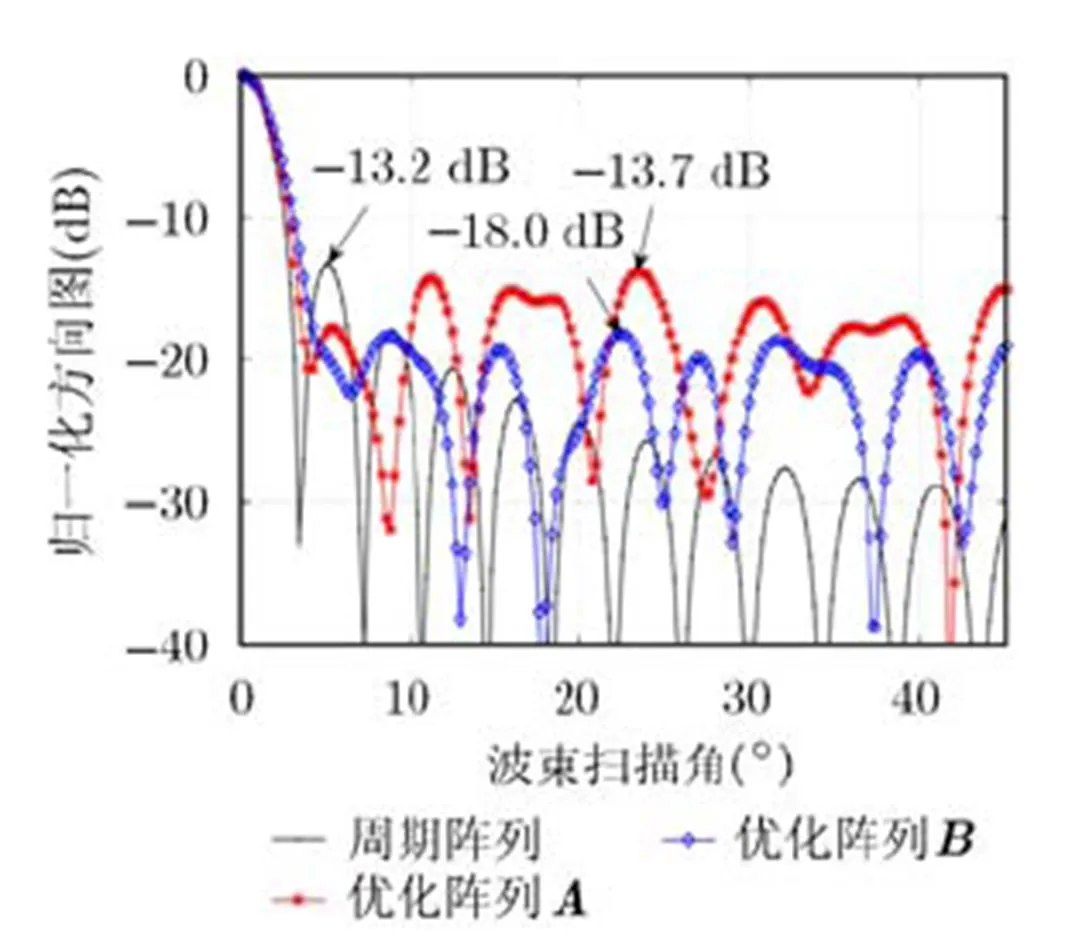
图4 多目标优化后的雷达阵列方向图

5 结束语

对于雷达-通信综合射频系统来说，如何灵活高效地配置共享孔径资源是提高系统整体性能的关键环节之一。本文从多目标优化的角度来处理共享孔径分配问题，首先建立了基于帕累托最优的多目标优化模型，然后提出了基于整数编码的改进粒子群算法，通过迭代求解以帕累托前沿的形式给出一组最优解，供决策者根据任务需求从中选择一个最满意的解。在仿真实验中，不仅对比分析了两种环境信息下所得帕累托前沿的异同，而且讨论了相同环境信息、不同任务需求下所得雷达阵列方向图的区别，从而验证了实现共享孔径动态分配的可行性与有效性。下一步将深入研究已知雷达系统杂波信息和通信系统信道状态信息情况下的共享孔径分配问题。

[1] TAVIK G C, HILTERBRICK C L, EVINS J B,. The advanced multifunction RF concept[J]., 2005, 53(3): 1009-1020. doi: 10.1109/TMTT.2005.843485.

[2] 张明友. 雷达-电子战-通信一体化概论[M]. 北京: 国防工业出版社, 2010: 1-15.

ZHANG Mingyou. The Conspectus of Integrated Radar- Electronic Warfare-Communication[M]. Beijing: National Defense Industry Press, 2010: 1-15.

[3] 吴远斌. 多功能射频综合一体化技术的研究[J]. 现代雷达, 2013, 35(8): 70-74.

WU Yuanbin. Research on technology of multifunction radio frequency integration[J]., 2013, 35(8): 70-74.

[4] QUAN Siji, QIAN Weiping, GUO Junhai,. Radar- communication integration: An overview[C]. 2014 IEEE 7th International Conference on Advanced Infocomm Technology (ICAIT), Fuzhou, China, 2014: 98-103. doi: 10.1109/ ICAIT.2014.7019537.

[5] 胡元奎, 靳学明, 范忠亮. 多功能综合射频系统技术研究[J]. 雷达科学与技术, 2015, 13(3): 233-239. doi: 10.3969/j.issn. 1672-2337.2015.03.003.

HU Yuankui, JIN Xueming, and FAN Zhongliang. Research on multi-function integrated RF system technology[J]., 2015, 13(3): 233-239. doi: 10.3969/ j.issn.1672-2337.2015.03.003.

[6] KHODIER M M and CHRISTODOULOU C G. Linear array geometry synthesis with minimum sidelobe level and null control using particle swarm optimization[J]., 2005, 53(8): 2674-2679. doi: 10.1109/TAP.2005.851762.

[7] HA B V, ZICH R E, MUSSETTA M,. Thinned array optimization by means of M-cGA[C]. 2014 IEEE International Symposium on Antennas and Propagation and USNC-URSI Radio Science Meeting, Tennessee, USA, 2014: 1956-1957. doi: 10.1109/APS.2014.6905305.

[8] WANG Xiangrong, ABOUTANIOS E, and AMIN M G. Thinned array beampattern synthesis by iterative soft- thresholding-based optimization algorithms[J]., 2014, 62(12): 6102-6113. doi: 10.1109/TAP.2014.2364048.

[9] 严韬, 陈建文, 鲍拯. 基于改进遗传算法的天波超视距雷达二维阵列稀疏优化设计[J]. 电子与信息学报, 2014, 36(12): 3014-3020. doi: 10.3724/SP.J.1146.2013.02011.

YAN Tao, CHEN Jianwen, and BAO Zheng. Optimization design of sparse 2-D arrays for over-the-horizon radar (OTHR) based on improved genetic algorithm[J].&, 2014, 36(12): 3014-3020. doi: 10.3724/SP.J.1146.2013.02011.

[10] FOSCHINI G J and GANS M J. On limits of wireless communications in a fading environment when using multiple antennas[J]., 1998, 6(3): 311-335. doi: 10.1109/TVT.2014.2363170.

[11] TELATAR E. Capacity of multi-antenna gaussian channels [J]., 1999, 10(6): 585-595. doi: 10.1002/ett.4460100604.

[12] POURAHMADI V, KOHANDANI F, and MOBASHER A. On the accuracy of channel modeling based on the Kronecker product[C]. 2010 IEEE 72nd Vehicular Technology Conference Fall (VTC 2010-Fall), Ottawa, Canada, 2010: 1-5. doi: 10.1109/VETECF.2010.5594341.

[13] LOYKA S L. Channel capacity of MIMO architecture using the exponential correlation matrix[J]., 2001, 5(9): 369-371. doi: 10.1109/4234.951380.

[14] GOROKHOV A. Antenna selection algorithms for MEA transmission systems[C]. 2002 IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Orlando, FL, USA, 2002, III: 2857-2860. doi: 10.1109/ ICASSP.2002.5745244.

[15] SANAYEI S and NOSRATINIA A. Capacity of mimo channels with antenna selection[J]., 2007, 53(11): 4356-4362. doi: 10.1109/ TIT.2007.907476.

[16] REYES-SIERRA M and COELLO C C. Multi-objective particle swarm optimizers: a survey of the state-of-the-art[J]., 2006, 2(3): 287-308.

[17] RAQUEL C R and NAVAL Jr P C. An effective use of crowding distance in multiobjective particle swarm optimization[C]. The 7th Annual conference on Genetic and Evolutionary Computation, Washington, DC, USA, 2005: 257-264. doi: 10.1145/1068009.1068047.

[18] KENNEDY J and EBERHART R. Particle swarm optimization[C]. IEEE International Conference on Neural Networks, 1995, 4: 1942-1948. doi: 10.1109/ICNN.1995. 488968.

[19] NANBO J and RAHMAT-SAMII Y. Advances in particle swarm optimization for antenna designs: real-number, binary, single-objective and multiobjective implementations[J]., 2007, 55(3): 556-567. doi: 10.1109/TAP.2007.891552.

[20] YUAN Quan and YIN G. Analyzing convergence and rates of convergence of particle swarm optimization algorithms using stochastic approximation methods[J]., 2015, 60(7): 1760-1773. doi: 10.1109/ TAC.2014.2381454.

[21] KNOWLES J and CORNE D. Approximating the nondominated front using the pareto archived evolution strategy[J]., 2000, 8(2): 149-172. doi: 10.1162/106365600568167.

[22] MAHETA H H and DABHI V K. An improved SPEA2 multi objective algorithm with non dominated elitism and generational crossover[C]. 2014 International Conference on Issues and Challenges in Intelligent Computing Techniques (ICICT), Ghaziabad, India, 2014: 75-82. doi: 10.1109/ ICICICT.2014.6781256.

[23] KARIMI F and LOTFI S. Solving multi-objective problems using SPEA2 and Tabu search[C]. 2014 Iranian Conference on Intelligent Systems (ICIS), Bam, Iran, 2014: 1-6. doi: 10.1109/IranianCIS.2014.6802566.

[24] DEB K, PRATAP A, AGARWAL S,. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]., 2002, 6(2): 182-197. doi: 10.1109/4235.996017.

[25] KONAK A, COIT D W, and SMITH A E. Multi-objective optimization using genetic algorithms: A tutorial[J].&, 2006, 91(9): 992-1007. doi: 10.1016/j.ress.2005.11.018.

Optimal Allocation of Shared Aperture in Radar-communication Integrated System Based on Pareto Optimality

SHI Changan①②LIU Yimin①WANG Xiqin①YU Peng②

①(Department of Electronic Engineering, Tsinghua University, Beijing 100084, China)②(Luoyang Electronic Equipment Test Center of China, Luoyang 471003, China)

In this work, considering a radar-communication integrated radio frequency system, a dynamic allocation method of shared aperture using relevant environmental information is proposed. Firstly, the shared aperture allocation task is formulated as a Multi-Objective Optimization (MOO) problem based on Pareto optimality, which uses the peak side-lobe level of radar array pattern and the channel capacity of Multiple Input Multiple Output (MIMO) communication system as its objective function. Then, an improved particle swarmoptimization algorithm based on integer encoding is proposed to solve the MOO problem. The iterative algorithm can find out a set of optimal solutions in the form of Pareto front, one of which can be chosen by decision makers as the most satisfactory solution according to mission requirements. Finally, the simulation results verify the effectiveness of the proposed method.

Shared aperture; Integrated radio frequency system; Multi-objective optimization; Particle swarm optimization; Pareto optimality

TN957

1009-5896(2016)09-2351-07

10.11999/JEIT151377

2015-12-08；

2016-05-13；

2016-07-04

国家自然科学基金(61571260)

The National Natural Science Foundation of China (61571260)

刘一民 yiminliu@tsinghua.edu.cn

石长安：男，1978年生，博士生，研究方向为雷达信号处理.

刘一民：男，1983年生，副教授，研究方向为雷达信号处理.