基于动态引导滤波的多尺度图像融合算法

洪 铭 柳培忠 汪鸿翔



基于动态引导滤波的多尺度图像融合算法

洪 铭 柳培忠 汪鸿翔

华侨大学工学院

该文基于动态引导滤波器（RGF）提出了一种新的图像多尺度表示方法，并将其应用到图像融合技术中。首先，使用RGF将输入图像用多种尺度的子图表示；然后，基于显著性检测获得输入图像的权重映射；最后使用基于递归滤波的加权融合方法得到最后的融合图像。多组图像融合实验的比较结果表明，相比于其它基于多尺度分解的融合算法，本文提出的融合算法更好地保持了输入图像的细节信息，融合图像的视觉效果更好。

RGF 显著性检测 递归滤波

1 概述

图像融合是指将相同场景下的不同图像合成一幅图，图像融合技术在计算机视觉、医学图像处理、遥感图像、特征提取等领域都有广泛应用[1]。融合后的图像通常能提供更充分的场景信息，并且更有利于人眼和机器识别[2]。

多尺度变换理论被广泛应用到各种图像融合技术中。基于多尺度变换的图像融合技术主要步骤包括：一是将输入图像分解成多种尺度的子图，二是根据给定的融合策略对分解子图进行加权融合，三是使用逆变换重构融合图像。其中图像分解过程通常使用各种金字塔技术，包括拉普拉斯金字塔（LP）[3]、低通滤波金字塔（RP）[4]和梯度金字塔（GP）[5]。除此之外，小波变换[6]和曲波变换[7]也经常用于图像融合领域。但是，由于这些多尺度变换方法通常会使用到上采样或下采样处理，从而使得融合后的图像丢失掉部分细节信息[8,9]，并且在变换时也会引入噪声，使得融合图像的边缘处产生圆晕效应。

本文基于动态引导滤波（RGF）提出了一种新的图像多尺度分析方法。其中，RGF是最近提出的一种边缘保持类平滑滤波器，也是一种尺度滤波器。通过改变RGF的参数可以得到各种尺度的平滑图像和细节图像，而且这种边缘保持类分解过程不会损失图像的细节信息。同时本文基于显著性检测获得输入图像的权重映射，然后使用基于递归滤波的加权融合方法得到融合图像。

2 动态引导滤波器

Zhang等[10]提出了一种新的基于尺度测量的边缘保持类滤波器——RGF（rolling guidance filter）。相比于其它边缘保持滤波器，RGF是基于迭代实现并且有着更快收敛的属性，简单、快速并且容易理解。RGF主要包含小结构移除和边缘恢复两个过程，能自动保存图像中的大尺度结构。

首先，使用高斯滤波器移除小结构。用表示输入图像，表示输出图像，为高斯滤波器的标准差，和是像素下标。高斯滤波器如式（1）所示：

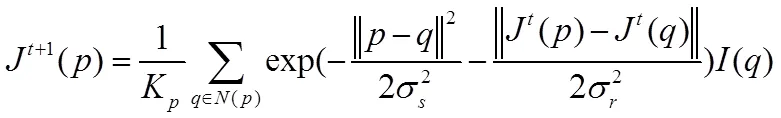
最后，将上述两个步骤结合起来，即从输入图像I开始进行动态引导滤波。如果为常量C，那么有=C，则式（2）变为，其形式与式（1）一样。

由图1可知，可以使用RGF移除图像中纹理、细节和噪声等小尺度结构，并且在移除这些结构时保存其它内容。同时由图1可知，当改变参数时，可以移除图像中各种尺度结构。图1是取不同值时RGF的滤波结果，最左边为输入图像，其它图从左到右的值依次为4、8、32；值都为0.05，迭代4次。

3 图像融合

将基于RGF的多尺度分解应用到图像融合过程中，主要包括多尺度子图获取、融合权重估计和加权融合3个过程。其中多尺度子图获取主要通过改变来移除不同的尺度结构；权重估计和加权融合使用的是一种基于递归滤波的加权融合方法，该过程先通过显著性计算分别获取各子图的权重，然后细化权重矩阵，最后加权融合各子图获得最终的融合图像。本文提出的图像融合流程如图2所示。

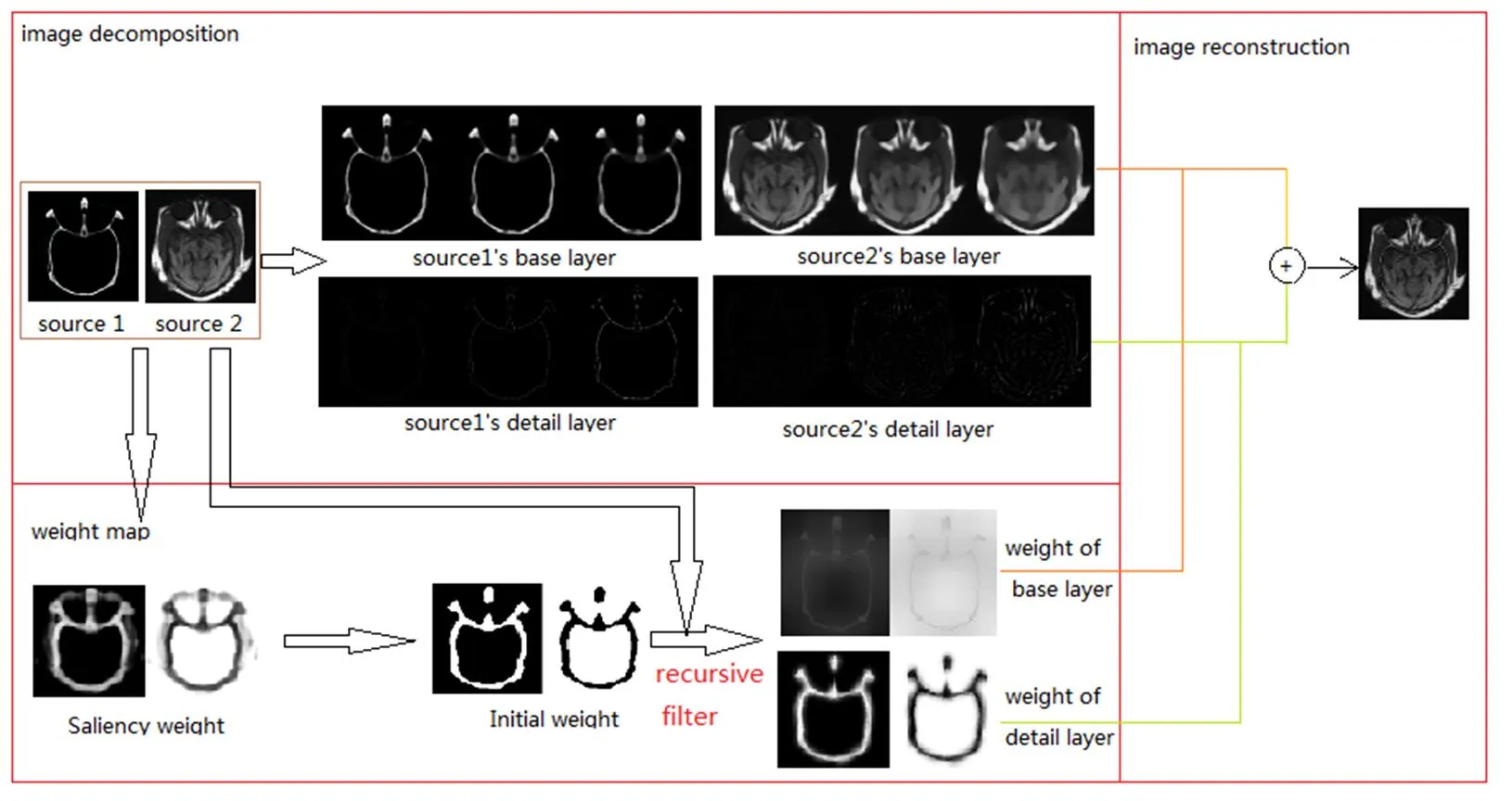
图2 图像融合流程图

3.1 获取多尺度子图

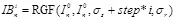
（4）

3.2 权重估计

由于人眼对于边、角和不平滑区域更加敏感，本文将文献[12]和[13]的3D采样方法应用到2D图像，得到显著性映射如下所示：

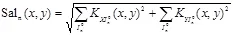
（6）

（8）

3.3 权重细化和加权融合

由图2可知，本文3.2小节中的权重估计充满了噪声和0、1权值。因此，本文采用一种基于递归滤波[14]的加权融合方法细化权重矩阵。递归滤波器是一种实时的边缘保持平滑滤波器。这里将输入图像作为参考图像，对权重映射进行递归滤波，得到基础层权重映射和细节层权重映射：

（10）

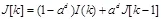
4 结果与分析

4.1 评估机制

为了客观评价图像的融合质量，本文采用归一化互信息QAB/F[11]和（MI）[13]两种评估机制来衡量算法的有效性。

MI表示融合图像从原图像获得的信息量的大小，具有对图像间重叠块大小不敏感的特征。设原图像为I1和I2，融合图像为F，则归一化互信息MI可由文献[13]中定义表示为：

其中，()、()和()分别表示A、B和F的边缘熵，而()表示A和F的互信息，且(,)=()+()-()，其中()表示A和F的联合熵。()的定义与MI(A,F)相似。

QAB/F表示融合图像对于原图像A、B的整体边缘信息保存量，其值可表示为：

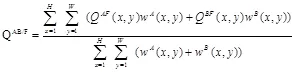
4.2 参数分析

在本文的所有实验中，设置多尺度分解的层数L=5。同时，RGF滤波器的初始=3，=0.05，然后逐级增大，步长step=2。引导滤波器的两个参数和对于本文算法有着一定的影响，当对基础层进行融合时，需要大尺度的和模糊度；当对细节层进行融合时，和不易太大和太小。因此本文采用默认设置，即：=25,=15,=0.01。

4.3 与其它基于多尺度变换算法的比较

为了验证本文算法的优越性和有效性，将其与其它基于多尺度变换的算法，如拉普拉斯金字塔（LP）、低通滤波金字塔（RP）、梯度金字塔（GP）、小波变换和曲波变换进行比较。比较算法的参数与文献[8]、[9]的设置一致。具体融合结果如图3～图5所示，表1为这几种算法的MI和QAB/F值。

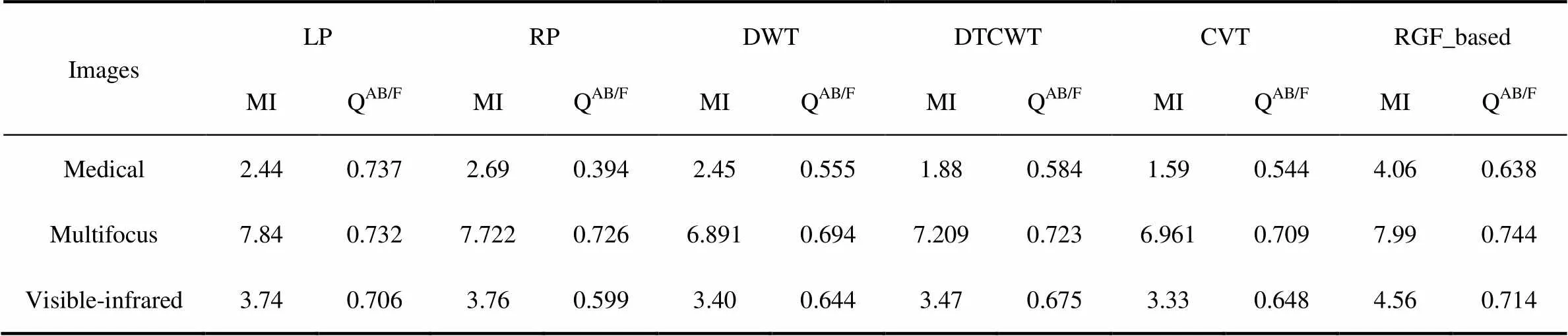
表1 本文算法（RGF_based）与其它基于多尺度变换的图像融合算法性能比较

图3是对Medical图像融合效果的比较，其中两输入图像具有互补的特征。可以看出，本文算法不仅能将两幅图中的重要信息保留下来，而且能保持比较好的对比度和清晰度。从表1也可以看出，本文算法取得了较高的MI值，表明本文算法能从原图像获得较多的信息量；同时本文算法的QAB/F值也比其他算法高，表明本文算法在融合过程中能有效保持输入图像的边界。

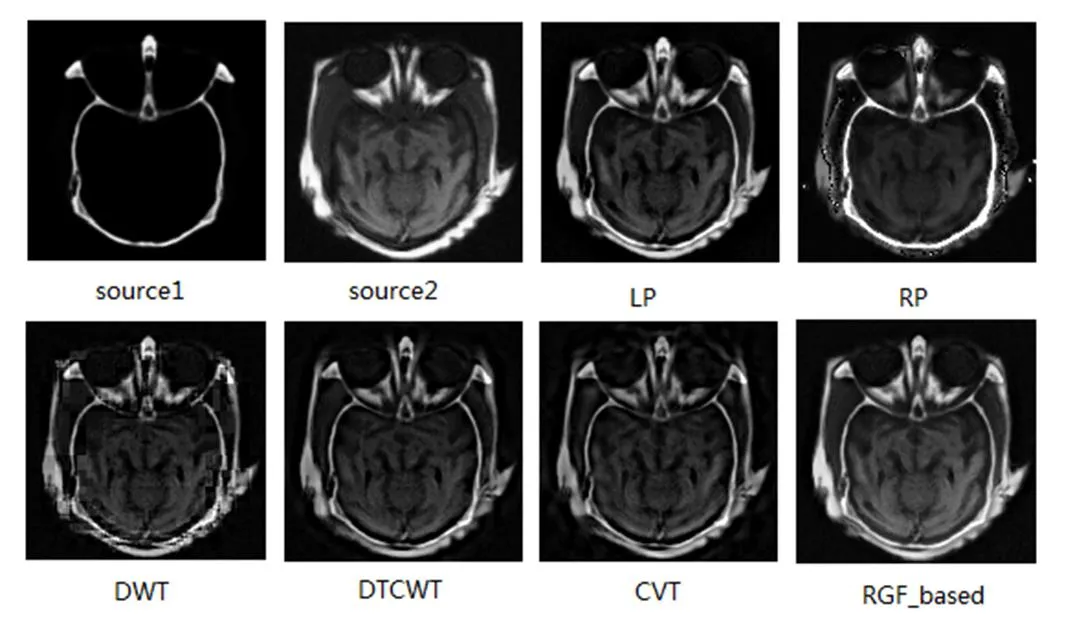
依次为输入图像1，输入图像2，LP，RP，DWT，DTCWT，CVT和本文算法的融合结果。

图4为Multifocus图像融合效果的比较，即两幅图像的聚焦不同。可以看出，两输入图像的特征和清晰度在融合图像中得到了保持，同时本文算法的对比度要稍好于其它算法。从表1的MI和QAB/F值可以看出差别，即本文算法较好地将源图像中的清晰部分保留下来了。

依次为输入图像1，输入图像2，LP，RP，DWT，DTCWT，CVT和本文算法的融合结果。

图5为可见光图像与红外图像的融合。可见光图像能够更好反映物体的细节，而红外图像能够有效捕捉发热目标，因而在融合图像中既有细节又有发热目标。可以看出，本文算法得到的融合图像对比度高，背景信息丰富，同时融合图像中的草丛相比于其它算法要更加清晰。从表1也可看出，本文算法的MI和QAB/F值都较高。

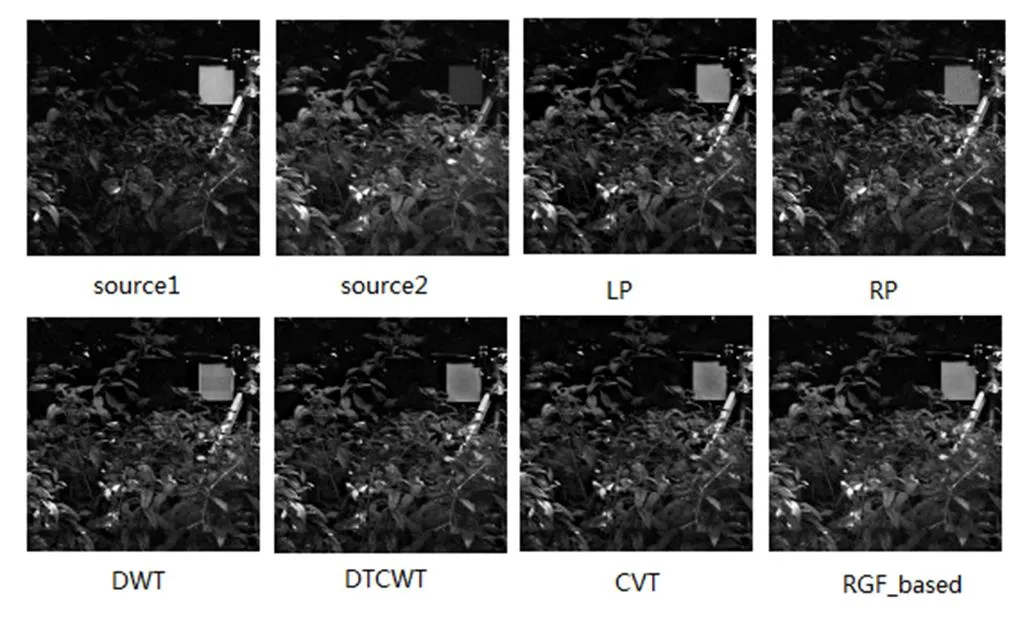
依次为输入图像1，输入图像2，LP，RP，DWT，DTCWT，CVT和本文算法的融合结果。

5 结论

本文基于RGF提出了一种新的图像多尺度表示方法，并将其应用到图像融合技术中。首先，使用RGF将输入图像用多种尺度的子图表示，再基于显著性检测获得输入图像的权重映射，最后使用基于递归滤波的加权融合方法得到最后的融合图像。多组图像融合实验的比较分析结果表明，相比于其它基于多尺度分解的融合算法，本文提出的融合算法更好地保持了输入图像的细节信息，融合图像的视觉效果更好。

参考文献：

[1] Goshtasby AA, Nikolov S.. Image fusion: Advances in the state of the art[J]. Information Fusion, 2007, 8(2): 114–118.

[2] Hall D L, Llinas J. An introduction to multisensor data fusion[J]. Proceedings of the IEEE, 1997, 85(1): 6−23.

[3] Burt P., Adelson E.. The laplacian pyramid as a compact image code[J]. IEEE Transcations on Communications, 1983, 31(4): 532–540.

[4] Petrovic V., Xydeas C.. Gradient-based multiresolution image fusion[J]. IEEE Transactions on Image Processing,2004, 13(2): 228–237.

[5] LI H., Manjunath B., Mitra S.. Multisensor image fusion using the wavelet transform[J]. Graphical Models and Image Processing, 1995, 57(3): 235–245.

[6] Lewis J., O’ Callaghan R., Nikolov S., et al.. Pixel- and region-based image fusion with complex wavelets[J]. Information Fusion, 2007, 8(2): 119–130.

[7] Nencini F., Garzelli A., Baronti S., et al.. Remote sensing image fusion using the curvelet transform[J]. Information Fusion, 2007, 8(2): 143–156.

[8] Piella G.. A general framework for multiresolution image fusion: from pixels to regions[J]. Information Fusion, 2003, 4(4): 259–280.

[9] LI S., YANG B., HU J.. Performance comparison of different multi-resolution transforms for image fusion[J]. Information Fusion, 2011, 12(2): 74–84.

[10] ZHANG Q., SHEN X., XU L., et al.. Rolling guidance fiter[C]//Computer Vision—ECCV 2014, 2014: 815–830.

[11] ZHAO Y., LIU Y., SONG R., et al.. A saliency detection based method for 3d surface simpli fication[C]//IEEE Conf. Acoustics, Speech and Signal Process., 2012, 889–892.

[12] LIU Y, LIU S, WANG Z. A general framework for image fusion based on multi-scale transform and sparse representation[J].Information Fusion, 2015, 24:147-164.

[13] LIU S., HE D., LIANG X.. An improved hybrid model for automatic salient region detection[J]. IEEE Signal Process, Lett., 2012, 19(4): 207–210.

[14] Eduardo S. L. Gastal, Manuel M. Oliveira. Domain Transform for Edge-Aware Image and Video Processing[J]. ACM Transactions on Graphics, 2011, 30(4): 193–202.