厄瓜多尔MS≥6.8级地震时空对称性及趋势判断
2016-10-14高新甜延军平
高新甜,延军平,董 婕
(陕西师范大学旅游与环境学院,西安 710062)
厄瓜多尔MS≥6.8级地震时空对称性及趋势判断
高新甜,延军平,董婕
(陕西师范大学旅游与环境学院,西安710062)
在全球化的背景下,重大自然灾害发生的频率不断加快,其危害对人们的生活造成了重大的威胁。地震灾害是重大自然灾害之一,其发生的频率虽然不高,但造成的人员伤亡和经济损失巨大。对地震进行趋势判断,其理论和现实意义重大。从时间和空间的角度对厄瓜多尔近一个世纪MS≥6.8级地震数据进行了分析,利用蝴蝶结构图和可公度结构系加强对时间对称性的分析,再经震源的经纬度迁移和空间迁移规律,判断得出,厄瓜多尔时间上在2015和2016年的信号较强,空间上在79°~81°W,1°N~1°S之间有发生MS≥6.8级地震的可能。可为地震灾害的趋势判断研究提供一定的参考,为后续研究工作提供一些启示。
可公度;时空对称性;蝴蝶结构图;空间迁移;厄瓜多尔
高新甜,延军平,董婕.厄瓜多尔MS≥6.8级地震时空对称性及趋势判断[J].华南地震,2016,36(2):41-49.[GAO Xintian,YAN Junping,DONG Jie.Space-time Symmetry and Tendency Judgement for Earthquakes with MS≥6.8 in Ecuador[J].South china journal of seismology,2016,36 (2):41-49.]
0 引言
目前,全球自然灾害发生的频率和强度都呈增加趋势,个别灾害的发生具有明显的偶然性,但是大量灾害的发生又具有它的集中性[1],而集中性的背后蕴含的规律,则是我们需要探讨研究的重点。通过揭示自然灾害内在时空规律,可以提高灾害防御能力,对增强灾害适应能力有显著的推动作用。在各大自然灾害中,地震灾害的破坏力极大,波及范围极广,强震在顷刻间对人类的生命财产造成巨大的威胁,准确判断地震的发生趋势,由表及里地逼近地震发生的物理机理,逐步提高地震灾害的趋势判断水平,对人类的生产生活具有实际意义。自然界事物之间存在一种秩序,自然现象的周期性有其客观的外在反应,地震作为一种自然灾害,是自然系统的一部分,从而也遵循着自然的规律,可公度就是利用周期性的原理对自然现象进行趋势判断[2],李双双、延军平[3]基于可公度方法研究的西太平洋俯冲带北部地区MS≥8级强震时空对称特征对地震趋势进行判断,并得到了较好的验证(2013年5月24日,俄罗斯鄂霍次克海发生8.2级地震)系列研究成果表明:利用可公度的方法分析地震的时空分布是有其研究意义的,而验证案例也使我们的研究具有一定的应用和实际价值,本文中基于可公度的研究方法,辅以蝴蝶结构图和可公度结构系,通过对震中点的经纬度迁移和空间变化规律,对厄瓜多尔的地震从时间和空间的角度进行了趋势判断。
1 研究区概况

图1 厄瓜多尔区位图及城市分布Fig.1 Location and city distribution of Ecuador
厄瓜多尔位于全球两大地震带之一的环太平洋地震带上。环太平洋地震带是全球地震活动最强烈的地区,地震释放能量约占全球总释放能量的76%,全世界大约80%的浅源地震,90%的中源地震以及几乎所有的深源地震都集中于此。研究该带地震的震相特征,对正确、迅速地测定地震参数十分重要[4]。厄瓜多尔大致位于2°N~5°S,75°W~81°W,东北同哥伦比亚毗邻,东南与秘鲁接壤,西临太平洋。厄瓜多尔地处南美太平洋地区,在大地构造上属南美大陆科迪勒拉-安第斯中新生代褶皱系。从东向西由6个构造带组成,即伊基多斯弧后盆地、次安第斯山脉区、主科迪勒拉山脉区、西科迪勒拉山脉区、安第斯山间地堑和北安第斯山脉区[5],构造活动强烈,地震频繁,属于地震活跃区域。
位于南极洲板块的科科斯板块从东太平洋海隆处被向东推移,俯冲消减于分属美洲版块的加勒比板块[6],形成一条经过厄瓜多尔的地震带。厄瓜多尔位于太平洋板块和美洲板块的交界处,系交错挤压所形成转换断层型边界。两板块进行持续的摩擦时,能量将以平均的方式持续较长的时间,此时多发生小型地震,但当两板块摩擦减缓,滑动速率减小时,会造成长时间能量的积累,而后以一次集中而大型的形式进行能量的释放,此时多发生大型地震灾难。
2 资料来源
目前国际上对震级的划分如下:1≤MS<3的地震,称为弱震或微震;3≤MS<4.5的地震,称为有感地震;4.5≤MS<6的地震,称为中强震;6≤MS<7的地震,称为强震;7≤MS<8的地震,称为大地震;8级以及8级以上的地震称为巨大地震[7]。据此可知MS≥6.8级地震会造成较大的破坏,本文主要选取厄瓜多尔MS≥6.8级地震作为研究对象具有一定的实际意义。
本文的地震数据来源于宋治平等人主编的《全球地震目录》[8]。重大自然灾害是一个有时空联系的灾害事件群[9],而地震作为重大自然灾害中危害最大的灾害之一,具有一定的时空分布规律。通过统计厄瓜多尔1890—2010年的地震数据,如表1所示,发生了22次MS≥6.8级的地震,其中1906年发生了三次。在此基础上,利用可公度方法计算,并构建可公度结构系和蝴蝶结构图对时间进行分析判断未来地震发生的年份,再利用震源的空间分布特征和经纬度的迁移规律判断震源的空间走向趋势。
3 时间对称性及趋势判断
时间对称性,即多周期叠加,主要通过三元可公度对称法、四元可公度对称法和五元可公度对称法等进行计算确定,其直观表现为蝴蝶结构图[10]。时间对称性包括时间平移对称性和时间反演对称性两种[11]。文中所引用的对称性是指前者,即时间平移对称性。地震活动在时间上还表现为强弱交替的韵律特征[12]。无论是在某一较大的地震区域还是在全球地震活动频次、地震震级和释放能量的大小在时间轴上都有分段起伏的韵律,每一起伏韵律都可分出强活动幕和弱活动幕两个时段。本文主要通过三元可公度对称法、四元可公度对称法和五元可公度对称法等对厄瓜多尔1896—2010年发生地震的年份进行计算,并绘制出对称性的蝴蝶结构图。在时间对称性方面,采用可公度信息提取方法和蝴蝶结构图法两种方法对部分重大自然灾害进行趋势预测,目的在于对不同方法的实用性验证[13]。
3.1可公度方法及其检验
可公度性是自然界的一种秩序,所以是一种信息系[2]。可公度 最早是由提丢斯和波特提出的,他们注意到太阳系星体围绕轨道运行天体的平均运动与其到轨道中心的主星的距离有关,并利用数学的数量给出平均运动的经验关系式,后成为著名的提丢斯波特定则[14]。可公度性亦是对称性规律的一种体现,其对称性既表现在时间上又表现在空间分布上,具有时空统一性[3]。由表1可知,1896—2010年厄瓜多尔MS≥6.8级地震发生次数为22次,同一年发生的地震在计算中取震级最大的一次,统计得出有20次,分别设其为X1-X20,并计算X21,X22
X1=1896,X2=1906,X3=1913,X4=1923,X5=1924,X6=1933,X7=1938, X8=1942,X9=1943,X10= 1949,X11=1950,X12=1955,X13=1956,X14=1963,X15=1971,X16=1987,X17=1995,X18=1998, X19= 2007,X20=2010,X21=?,X22=?
可公度检验是以可公度性为基础,利用之前发生地震的年份统计通过可公度式对厄瓜多尔的研究年份进行逐个检验,从而来判断研究区域的可公度性。分别利用三元、四元、五元的可公度式计算,对结果进行频数统计,并对已经发生地震的20个年份进行可公度检验,检验结果表明:除个别年份,有17个年份都有10个及其以上的可公度性(图2),表明厄瓜多尔的历史地震具有良好的可公度性。
在验证了厄瓜多尔的历史地震有较好的可公度性后,以这20个年份数据作为基础数据来对厄瓜多尔地震灾害的趋势预测。据表2可知,2016年在三元可公度计算结果中具有最高的频数6,2015年在四元的可公度计算结果中具有最高的频数46,2015年和2016年在五元的可公度计算中都有较高的频数。由以上的计算结果可推知:2015年和2016年的地震信号较强,地震的发生趋势比较明显,有发生6.8级以上地震的可能。
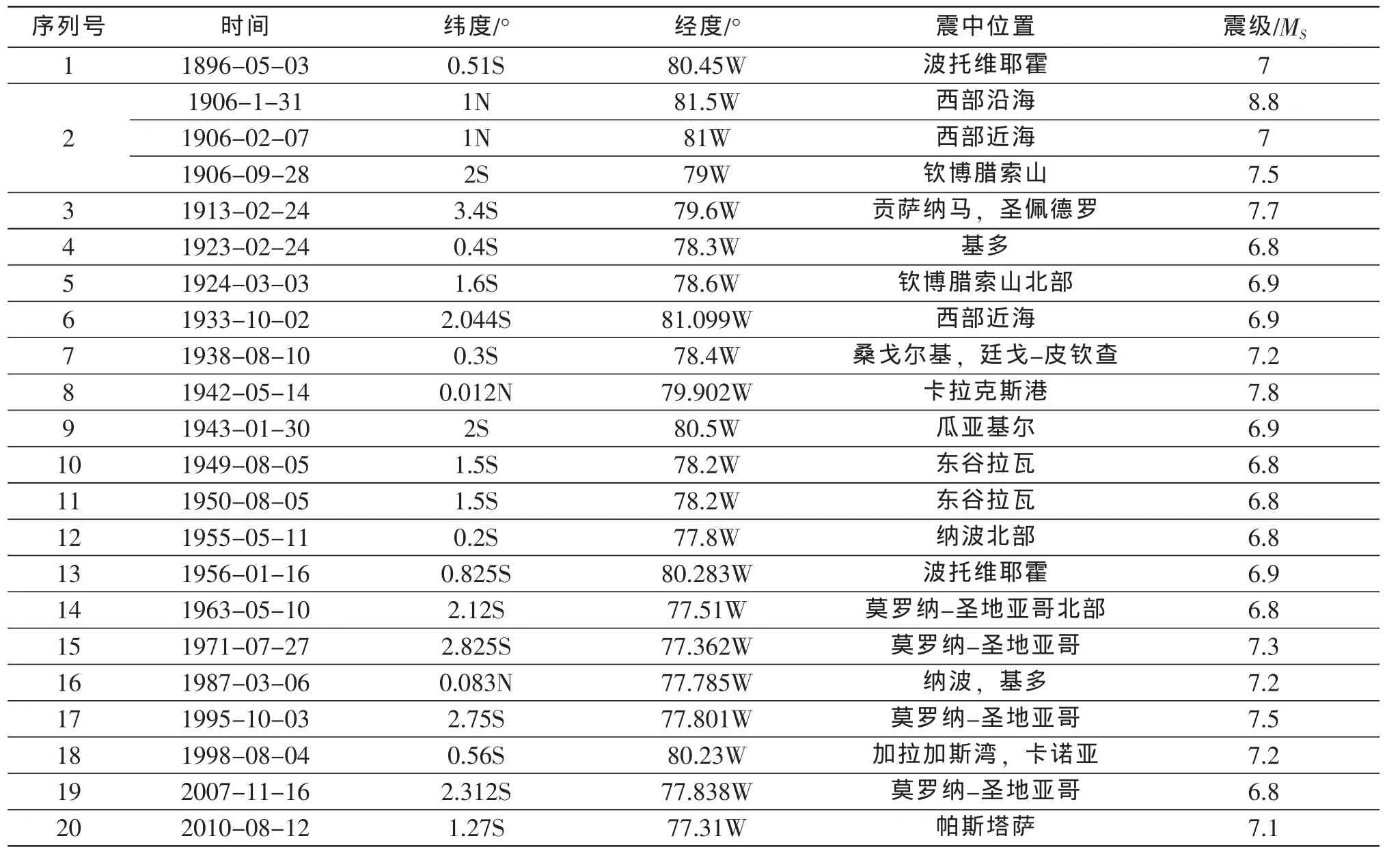
表1 厄瓜多尔1890-2010年MS≥6.8地震参数Table 1 Seismic parameters of earthquakes with MS≥6.8 in Ecuador during 1890 and 2010
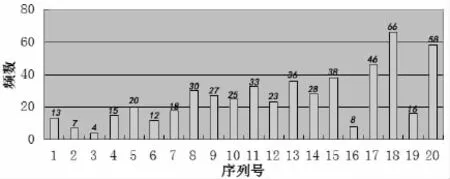
图2 可公度方法检验的年份频数Fig.2 The year frequency tested by the commensurability method
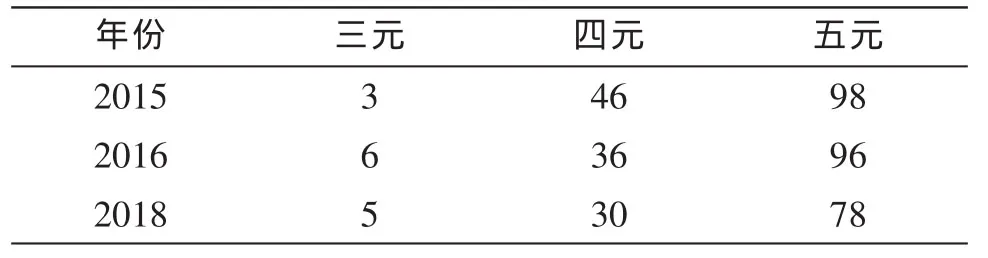
表2 可公度趋势判断的频数统计Table 2 Frequency statistics of the commensurability tendency judgement
3.2蝴蝶结构图法
蝴蝶结构图法是建立在等时间间隔基础上,剖析时间对称性的一种方法[15]。通过构建年份结构关系,绘制具有时间对称性特点的蝴蝶结构图,20个灾害事件至少要有4~5个成组要求,以此来确定预测年份,给出预测结果的随机性概率和不漏报置信水平。根据对厄瓜多尔1896—2010年的地震数据分析得到的可公度信息,绘制出蝴蝶结构图,并发现了一些规律。
从图3中可以看出,厄瓜多尔的地震时间序列具有一定的周期性,时间间隔以74 a,65 a,44 a,27a,9 a,8 a较为显著,与2015年相关的主周期有四组,分别为65 a,44 a,8 a等。与2016年相关的主周期有2组,分别为74 a,9 a。根据主周期计算出蝴蝶结构预测年份的随机性概率:T=m/n,不漏报置信水平:(1-a)=m/n+1,T为预测年份发生的可能概率,n为总灾害事件次数,m为参与实际预测的灾害次数,a为不漏报置信水平。经计算,2015年、2016年厄瓜多尔发生MS≥6.8级以上地震的可能性分别为50%,45%,不漏报置信水平为52.4%,57.1%.
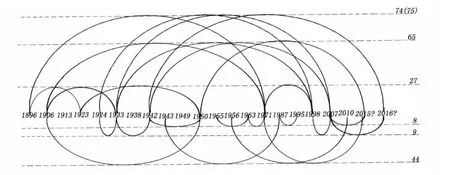
图3 厄瓜多尔MS≥6.8地震蝴蝶结构图及趋势判断Fig.3 The butterfly structure map and trend of earthquakes with MS≥6.8 in Ecuador
3.3可公度结构系法
可公度结构是指从已经发生地震的年份中筛选一种或几种与主周期相关的年份,然后根据时间间隔即周期关系构建一种类似于网状的结构,利用这种结构关系可进一步验证推演下一次地震的发生年份[15]。经可公度计算,2015年和2016年厄瓜多尔发生MS≥6.8级地震信号较强,有可能发生较大的地震。那么从1896年以来发生地震的年份选取部分与周期74 a、65 a、9 a、8 a相关的年份加上推测出来的年份,构建可公度结构系,图中呈现出了明显的对称结构。
如图4所示的2013年可公度结构系,短活跃地震期可被视为一组数据构建可公度结构系。主题表现为以主周期9 a、11 a和74 a形成的矩形和从上到下,从左到右平移对称,根据这种对称形式的发展趋势判断2016年可能发生地震;以主周期27 a、9 a、8 a和65 a组成的对称矩阵的发展趋势判断2015年可能发生地震,此外,主体为主周期65 a、13 a、24 a和 8a也表现出一定的对称性,以此对称结构可判断2015年可能发生地震。以上3种对称形式综合分析主周期与2015年和2016年关联性最好,即2015年和2016年最有可能发生地震,此结果很好的佐证了由可公度法计算出来的结果。
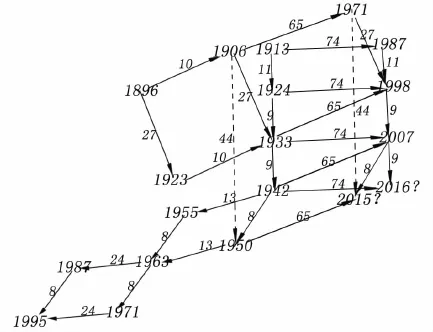
图4 厄瓜多尔MS≥6.8地震可公度结构系Fig.4 Commensurable structure of earthquakes with MS≥6.8 Ecuador
4 空间对称性及趋势判断
空间对称性指几何空间配置上的对称性,是被观察对象相对于某一事物经过空间位置转换后和变化前相似的性质。本文主要是通过探索灾害空间对称性的不同形式,判断灾害发生的空间趋势。同一级别断层之间的间距均匀,同一级别的重大地震灾害更具有空间对称性。
4.1震中分布及其对称性
如图5所示,厄瓜多尔1896—2010年MS≥6.8级的震中分布大致以79°W和1.4S为对称轴,震中在对称轴的两侧基本呈等量分布。通过对厄瓜多尔地形的现状分析,发现在对称轴79°W附近有山脉经过,这与震中的分布有一定的关系。
4.2地震震中的经纬度迁移
地震迁移是理解地震现象本质的一个重要问题[16]。国内外也有多次用震中迁移现象预报大地震的实例,地震震中的迁移也逐渐成为人们预测地震发生过程中考虑的重要因素。本文对20个灾害事件的经纬度进行分析,图6为厄瓜多尔强震震中经向、纬向迁移图,据图分析判断得出下一次地震发生地点经纬度的迁移趋势。
如图6所示,分析地震震中纬向迁移,可以看出历史地震大致以1.4°S为对称轴上下摆动,经度方向上,则以79°W为对称轴摆动。综合分析震中经纬向迁移,可看出两者迁移的同步性。假设区域的迁移规律不变化,第21次的震中迁移方向为经向震中向西迁移,纬向震中向北迁移。
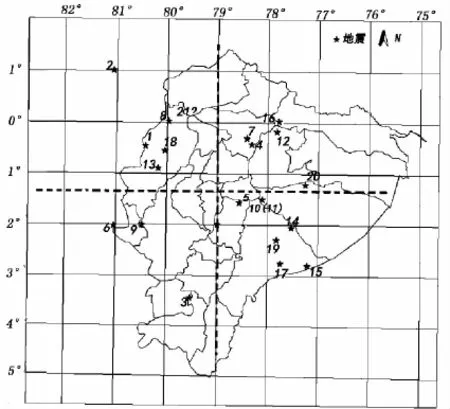
图5 厄瓜多尔1890—2010年MS≥6.8地震震中分布Fig.5 Distribution map of earthquake epicenters with MS≥6.8 in Ecuador during 1890 and 2010
4.3震中空间迁移特征
空间对称性主要可表现为多边形的空间对称,地震空间对称的几何表现形式,主要归类为直线对称、三边对称、四边对称和多边对称等[15]。所以对1896—2010年厄瓜多尔MS≥6.8级的22次地震中按发生的顺序分析,在该过程中,我们将同一地点和同一年发生的地震按一次事件对待,经过筛选后有19个震中点(即序号为10和11两次地震为一个震中点)作为空间迁移的研究对象,构成了5个四边形和7个三角形,进而找出下一次发生地震的可能位置。
将19个震中点分为4组,4个震中点为一组,如表3所示,分析发现100%的四边形都跨过了对称轴1.4°S,75%的四边形跨过了对称轴78°W,说明具有很好的四边形空间对称分布特性。归纳总结前4个四边形的规律,发现第5个四边形的迁移趋势可能是逆时针,第19个震中点向第20个震中点的迁移方向为东-西,南-北,且根据震中点在对称轴两侧分布规律可知第5个四边形中,第20个震中点在对称轴79°W的左侧,满足此迁移规律的范围如图7所示,即下一次地震发生位置可能为79°~81°W,1°N~1°S之间。
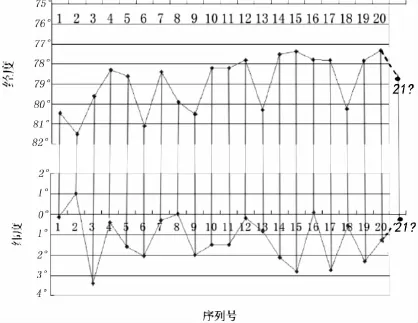
图6 厄瓜多尔MS≥6.8地震震中的经纬度迁移Fig.6 The latitude and longitude migration map of earthquake epicenters with MS≥6.8 in Ecuador

表3 四边形迁移规律Table 3 Quadrilateral migration rule
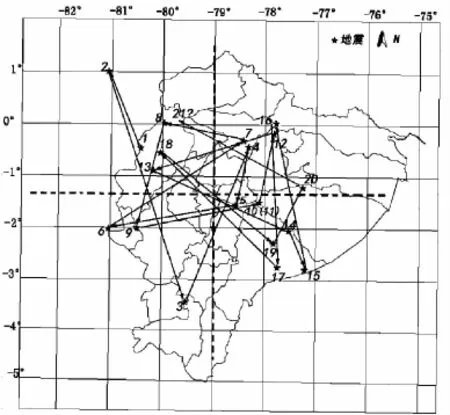
图7 厄瓜多尔MS≥6.8地震震中的空间迁移图Fig.7 Space migration map of earthquake epicenters with MS≥6.8 in Ecuador
将19个震中点分为6组,3个为一组,如表4所示,第2个和第3个三边形在对称轴的东北西南方向形成对称关系;第1个三角形两点在对称轴以北一点在对称轴以南和第5个三边形两点在对称轴以南一点在对称轴以北形成对称关系;第6个三边形两点在对称轴以东一点在对称轴以西和第7个三边形两点在对称轴以西一点在对称轴以东形成对称关系,此外,第4个三边形两点在对称轴以北与第2个三边形两点在对称轴以南形成对称关系,第四个三边形两点在对称轴以东与第3个三边形两点在对称轴以西形成对称关系。以此7个三角形形成的对称关系,则可推断出下一次地震发生位置可能为79°~81°W,1°N~1°S之间。这与四边形迁移规律得出的结论基本一致,更具说服力。
5 结语
本文利用可公度的研究方法,分别从时间和空间的角度对厄瓜多尔MS≥6.8级地震进行分析,得出的主要结论如下:
(1)经可公度方法检验和计算得出,1896—2010年厄瓜多尔MS≥6.8级历史地震具有较好的可公度性,2015,2016年厄瓜多尔发生MS≥6.8级地震的信号较强。
(2)厄瓜多尔MS≥6.8级地震震源的经纬向迁移呈现出较好的对称性,以1.4°S和79°W为对称轴,假设区域的迁移规律不变化,第21次的震中迁移方向将为经向震中向西迁移,纬向震中向北迁移。
(3)厄瓜多尔MS≥6.8级地震震中的空间分布具有一定规律,利用对称性原理进行分析得出第21次震中点的迁移方向应该是东→西,南→北,发生地点为79°W~81°W,1°S~1°N之间。
(4)本文主要是在前期相关研究的基础上,完善了蝴蝶结构图法和可公度结构系法在对地震发生的时间趋势判断的运用,也增加了三边形和四边形迁移规律在对地震空间趋势判断的运用。
(5)本文利用可公度的方法,通过对地震时间和空间资料的分析和观察,将对称性的原理应用于地震活动的趋势分析,尝试对地震的发展趋势进行探讨,旨在为地震的发生趋势判断提供一定的理论方法,为实时的地震预测提供一定的参考依据,将可公度方法研究出的规律与地质预测和物理预测互相结合,减少地震为人民的生产生活带来的损失。

表4 三角形迁移规律Table 4 Triangle migration rule
[1]王铮.近40年来中国自然灾害的时空统计特征[J].自然灾害学报,1994,3(2):16-21.
[2]翁文波.预测论基础[M].北京:石油工业出版社,1984.
[3]李双双,延军平.西太平洋俯冲带北部地区MS≥8强震时空对称特征[J].地球物理进展,2012,27(3):960-966.
[4]赛来义,魏斌,阿下木.喀什台环太平洋地震带地震记录特征[J].内陆地震,1996,10(3):281-285.
[5]唐尧,连卫,郑厚义.厄瓜多尔地质矿产特征及找矿远景分析[J].地质与矿产,2013,39-41.
[6]韩啸,董婕,延军平,等.墨西哥MW≥7.5地震时空对称性及趋势研究[J].内陆地震,2015,29(1):28-36.
[7]曾倪俊.地震震级如何划分[J].四川统一战线,2013 (5):33.
[8]宋治平.全球地震灾害信息目录[M].北京:地震出版社,2011.
[9]李双双,延军平,刘栎杉,等.印度尼西亚 MS≥7.8强震时空对称特征及其趋势判断[J].自然灾害学报,2013,22(1):190-197.
[10]延军平,李双双,刘新颜,等.基于对称性的中国台湾地震趋势判断及物理基础[J].灾害学,2013,28 (1):11-14.
[11]李奴义.浅谈对称概念及其在自然科学中的意义[J].青海师范大学民族师范学院学报,2002,13(2):48-49.
[12]黄建平,石耀林,苏小宁.环太平洋地震的时空特征分析[J].地震,2013,33(4):115-122.
[13]延军平,白晶,苏坤慧,等.对称性与部分重大自然灾害趋势研究[J].地理研究,2011,30(7):1 160-1 168.
[14] NietroM M.The Titius Bode Law of Planetary Distances,Its history and theory[M].New York:Pergamon Press,1972.
[15]延军平.重大自然灾害时空对称性研究[M].陕西:陕西师范大学出版社,2013.
[16]郭增建,秦保燕.地震迁移问题综述[J].国际地震动态,1983,4(1):8-10.
Space-time Symmetry and Tendency Judgement for Earthquakes with MS≥6.8 in Ecuador
GAO Xintian,YAN Junping,DONG Jie
(College of Tourism and Environment Science,Shaanxi Normal University,Xi'an 710062,China)
Under the background of globalization,the frequency of the major natural disasters is accelerating,with the major threat following.Earthquake is one of the major natural disasters.Although earthquake happened with a low frequency,the economic losses and casualties caused by earthquake are huge.It will be of great significance in reality and theory to do study on earthquake tendency.This paper analyzes the seismic data about MS≥6.8 nearly a century of Ecuador from the viewpoint of time and space,and further does the time symmetry analysis by using the butterfly structure and commensurability structure system and the law of the hypocenter migration about latitude-longitude and space.It comes to the conclusion that there is a strong earthquake signal during 2015 and 2016.And it is likely to happen MS≥6.8 earthquake in 79°-81°W,1°N-1°S of Ecuador.Theresearch can offer some reference for the trend analysis of earthquake disasters and provide some enlightenment for future research.
Commensurability;Symmetry;Butterfly structure;Space migration;Ecuador
P315.7
A
1001-8662(2016)02-0041-09
10.13512/j.hndz.2016.02.007
2015-10-06
国家社会科学基金重点项目 “西部重大灾害时空规律的统计研究”1202050208(655278)
高新甜 (1990-),女,硕士研究生,主要从事气候变化与人类适应研究.
E-mail:15902939187@163.com.
