用于电能质量预测分析的交流电弧炉时变参数模型
2016-10-14廖延涛胡骏张海龙王恩荣
廖延涛胡 骏张海龙王恩荣
(1. 南京师范大学电气与自动化工程学院,南京 210042;2. 南京师范大学物理科学与技术学院,南京 210023)
用于电能质量预测分析的交流电弧炉时变参数模型
廖延涛1胡骏1张海龙2王恩荣1
(1. 南京师范大学电气与自动化工程学院,南京210042;2. 南京师范大学物理科学与技术学院,南京210023)
基于能量守恒定律建立了一种以微分方程描述的交流电弧炉(EAF)时域模型,模型以电弧导纳作为状态变量,电弧电流和弧长作为输入,进一步根据弧长与电弧电压关系式推导出模型参数与弧长的关系,并给出时变参数的工程估算方法。以实际炼钢交流电弧炉为例,将带通白噪声信号叠加在弧长上模拟实际工况,分别对熔化期和精炼期电弧炉的动态特性以及电网的电压波动和谐波进行仿真研究,仿真结果与实测数据相吻合,证明了模型的有效性和实用性。
电弧炉;电弧阻抗;时变参数;电能质量;负荷建模
交流电弧炉作为一种冲击性的非线性负荷,对供电网络造成了种种负面影响,包括谐波、电压波动和闪变、三相不平衡以及有功冲击和无功冲击等电网污染,这对于电力系统的安全稳定运行是极为不利的[1-3]。
为了分析并解决上述由交流电弧炉引起的电网污染问题,建立精确、实用的交流电弧炉数学模型至关重要[4]。近年来,许多国内外学者对交流电弧炉的建模问题进行了大量研究[5-14]。通过实际电弧U-I特性曲线拟合的方法是目前应用较多、研究较为深入的方法[5-6]。该方法原理直观明了,所需参数易于获取,可用于谐波和电压波动等电能质量的研究。但该模型依赖于负载消耗的实际有功功率,由于不同电弧炉的特性多样性,参数难以准确地预估,仿真结果未免引入较大误差,并且没有考虑电弧的物理特征,无法体现弧长的随机变化是导致电压波动的根本原因[7]。基于能量平衡关系建立的动态电弧模型能够从系统的运行环境和电弧的微观变化上反映出电弧炉的实际动态特性[8-11]。模型从电弧的内在因素出发推导外部特性,将电弧作为一种非线性时变的电路元件接入供电系统仿真,能够分析不同电弧炉引起的电能质量问题,具有较高的准确性和通用性。但由于模型参数的取值没有明确的物理依据,往往需要依靠经验或实测数据辨识,因此不适用于工程预测。文献[12]基于电弧热学原理,将电弧等效为非线性时变电阻,建立了电弧炉时变电阻模型。模型中的每个参数都有明确的物理意义,对于吻合实际电弧炉的运行特性有直观的优势,但研究对象一般为吨位较小的电弧炉。另有诸多文献采用实测数据注入模型的方法对电弧炉引起的电能质量问题进行了深入研究[13-14]。然而,电弧炉作为一种时变系统,电弧具有高度的随机性和时变性,模型参数的取值应当随着弧长时刻变化,这在目前已报道的模型中并没有得到体现。
鉴于此,本文提出一种模型参数随弧长时序变化,适用于电能质量分析和工程预测的交流电弧炉模型。模型基于能量守恒定律建立,利用电弧炉系统的初始设计参数以及电弧的时变特点确定模型参数的估算方法,以避免传统模型依赖实测数据辨识以及采用固定参数来模拟电弧炉时变系统的不足。通过实际炼钢电弧炉为例进行仿真,以验证模型的有效性以及对于电网电能质量预测分析的准确性。
1 模型建立与参数估计
1.1模型建立
如图1所示为三相交流电弧炉电气系统示意图,钢厂主变压器将高压电网电压降压后接入炉用变压器一次侧,然后通过短网输送低电压大电流至电极,从而产生电弧。
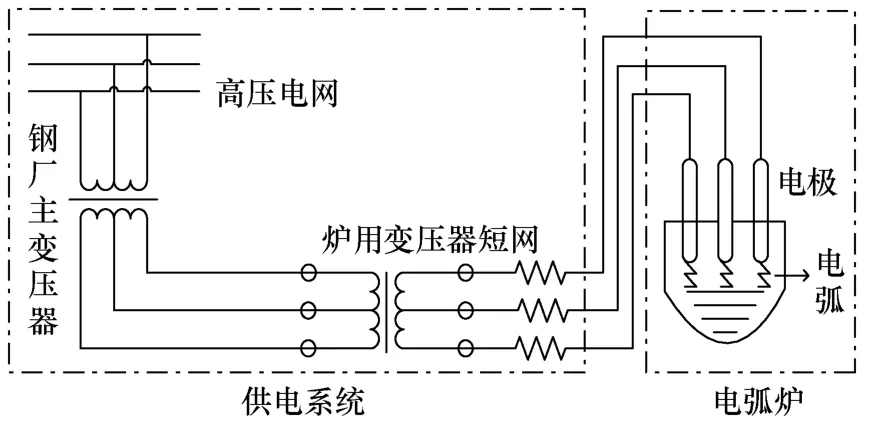
图1 三相交流电弧炉电气系统示意图
由能量平衡原理可得

式中,q为电弧弧柱中积累的能量;u为电弧电压;i为电弧电流;S0是电弧弧柱的视在功率损失。
将模型表示成导纳的形式,式(1)转化为

式中,y为电弧导纳。
根据气体分子运动论,得到电弧弧柱中积累的能量为[15]
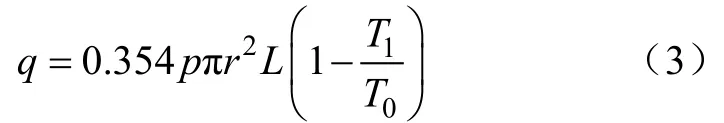
由沙哈公式推导出电弧电导率方程为

式中,σ为电弧电导率;σ0、m为常数,m取值为1.6014×104K[16]。
根据式(4)可推得电弧导纳y为

将式(3)至式(5)代入式(2),整理得

式中,参数k的表达式为
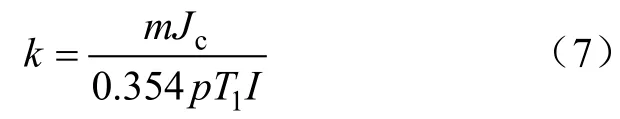
电弧损失的视在功率与电弧导纳的关系式为

式中,Uarc是电弧电压有效值。
将式(8)代入式(6),整理得

1.2参数估计
图2所示为电弧炉单相等效电路图,其中 Up表示电弧炉变压器与档位电压对应的相电压,rt为变压器内部电阻,Lt为变压器内部电感,rd为短网电阻,LdM为短网电感,Zarc为电弧阻抗。

图2 电弧炉单相等效电路图
当电流大于 100A时,电弧电压有效值 Uarc与电弧长度L的关系可以表示为[17]

式中,α为电弧阳极和阴极的电位降;β为弧柱梯度,α和β的值取决于电弧炉的冶炼时期[18]。
对于图2,根据欧姆定律可得

式中,I为电弧电流有效值;ω为供电电压的角频率。
结合式(10)和式(11),进一步推导出电弧电流有效值与弧长之间的关系如下

结合式(9)至式(12)得到提出的交流电弧炉时变参数模型为

可以看出,模型参数Uarc(L)和k(L)均与L相关,Uarc(L)体现了弧长与电弧电压的关系,而弧长与电弧电流、电弧半径的关系隐含在k(L)中。随着L的瞬时变化,模型参数也时刻变化,所描述的电弧伏安特性应当更加契合实际冶炼工况下的伏安特性,这正是本文提出时变参数模型的创新之处。同时,该模型还具有参数少且求解简便的优点,重要的是模型参数不依赖于现场数据采样辨识,从而具有更优异的普适性。
2 算例分析
以某钢厂 40t电弧炉为例[11],根据系统的实际参数,分别就熔化期和精炼期对电弧炉系统进行仿真,并将仿真结果与钢厂提供的实测数据进行对比。如图3所示,根据式(13)建立电弧仿真模型,进一步建立供电系统仿真模型。系统参数为:钢厂主变压器将110kV的高压电网电压变为35kV,低压侧电路等效阻抗为0.256Ω,通过炉用变压器将电压降到420V,短网电阻为0.4mΩ,短网电抗为2.496mΩ,钢厂主变压器的额定容量为63MVA,炉用变压器的额定容量为22MVA,内部电阻为0.069mΩ,内部电感为0.0022mH。
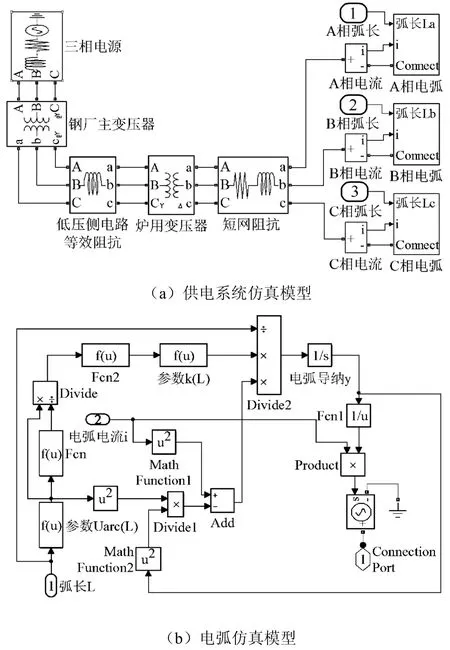
图3 三相交流电弧炉电气系统仿真模型
在实际运行中,由于受电磁力和炉料移动等因素影响,弧长的变化呈现出复杂的随机特性,在不同的冶炼时期由于功率需求不同,其弧长变化范围也不同。熔化期的弧长波动剧烈,形状呈细长状,而精炼期的弧长波动相对稳定,形状呈短粗状[18]。本文采用在最大弧长基础上叠加带通白噪声信号的方法来模拟不同冶炼时期弧长变化的随机性,计算表达式为

式中,L0=(Up−α)/β为最大弧长;Wnoise(t)为带通白噪声,频率范围选取4~14Hz[19]。
2.1熔化期运行特性
在熔化期,由于电弧一般较细长,并且炉温较低,所以电弧不易稳定,弧阻抗的非线性较强,电弧电压和电流波动较剧烈,对电网造成的电压波动和谐波也较为显著,由于维持长弧所需的能量更多,所以燃弧电压和熄弧电压都较高。根据文献[18]中关于电弧电位分布的研究成果,α取值为40V,β取值为10V/cm,炉温设为1150K,参照式(14)计算出熔化期弧长的理论波动范围为0~20.25cm。本文暂不考虑极端工况,将弧长波动范围选取为12~20cm[20],如表1所示,Uarc(L)和k(L)分别在160~240V和0.2507~8.275cm·W-1·s-1范围内随机变化并且在时序上是连续的。

表1 不同冶炼时期的电弧炉模型参数比较
根据电弧炉的动态特性,验证所提出模型的准确性,观察指标选为电弧电流、电弧电压以及电弧伏安特性,如图4所示,弧长的变化导致电弧电流和电弧电压剧烈波动,电流过零点处的伏安特性曲线倾斜度高,电流变化缓慢,“零休”现象明显,即此时电弧的非线性较强,说明本文提出的时变参数模型能够准确地模拟熔化期的电弧特性。
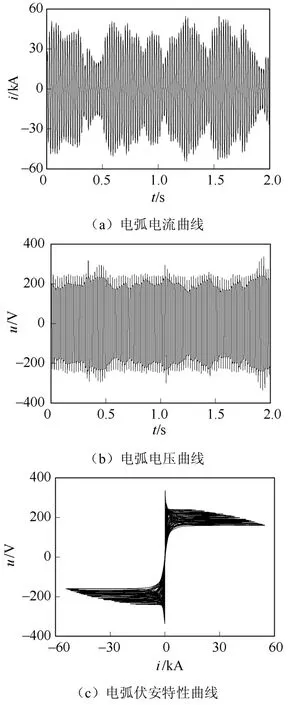
图4 熔化期电弧炉的动态特性
进一步观察电弧炉引起的电网电压波动以及谐波,以验证模型的实用性。国标GB/T 12326—2008《电能质量电压波动和闪变》中给出的电压波动d的定义表达式为

式中,ΔU为电压方均根值曲线上相临两个极值之差;UN为系统标称电压。
如图5所示,依据仿真得到的35kV母线上电压Ud的数据,应用式(15)计算电压波动,得到最大电压波动值为3.47%,超出国标限值的3%,与实测值3.3%基本一致。

图5 熔化期35kV母线A相电压曲线
从表2可看出,熔化期谐波电流的仿真结果与实测数据比较,两者不仅整体趋势一致,从定量的角度观察,也比较接近,尤其是2次谐波和各奇次谐波,误差较小。根据国标GB/T 14549—1993《电能质量公用电网谐波》中公布的谐波电流允许值,5次和7次谐波电流超出国标允许值12A和8.8A,在接入电网前需要治理。

表2 35kV母线A相谐波电流分析结果
2.2精炼期运行特性
在精炼期,电弧呈短粗状,炉温升高,电弧趋于稳定,弧阻抗的非线性降低,电弧电压和电弧电流比较稳定,引起的电网电压波动和谐波也较小,由于维持短弧所需的能量少,所以燃弧电压和熄弧电压都很低。根据文献[18],α取值为20V,β取值为5V/cm,炉温设为1800K,将弧长变化范围选为8~10cm[20]。从表1中可以看出,当弧长波动呈现出不同的剧烈程度和趋势时,参数也呈现出与熔化期不同的随机特性。由式(13)可知,Uarc(L)和k(L)与弧长呈负相关,弧长降低必然导致二者数值下降。实际物理含义为:由于弧长降低,维持电弧所需的能量减少,从而导致电弧电压有效值 Uarc(L)降低;而电流增大,电弧半径增加,炉温升高,也必然导致 k(L)的降低。另外,相对稳定的电弧使得Uarc(L)和 k(L)的波动剧烈程度下降,说明模型参数对于冶炼时期以及弧长变化的追踪性能良好。
电弧炉的动态特性如图6所示,对比图4可以看出,精炼期电弧电流和电压的波形变得平稳,由于弧长降低,燃弧电压和熄弧电压的幅值也大幅下降,电弧电流增大。特别地,在电弧电流过零点处,由于燃弧电压降低,伏安特性曲线的轨迹由尖锐变得平缓;电弧电流增大,非线性减弱,“零休”现象不如熔化期显著,导致伏安特性曲线的倾斜度降低。同样地,35kV母线A相电压曲线如图7所示,其最大电压波动值为1.17%,未超出国标限值。
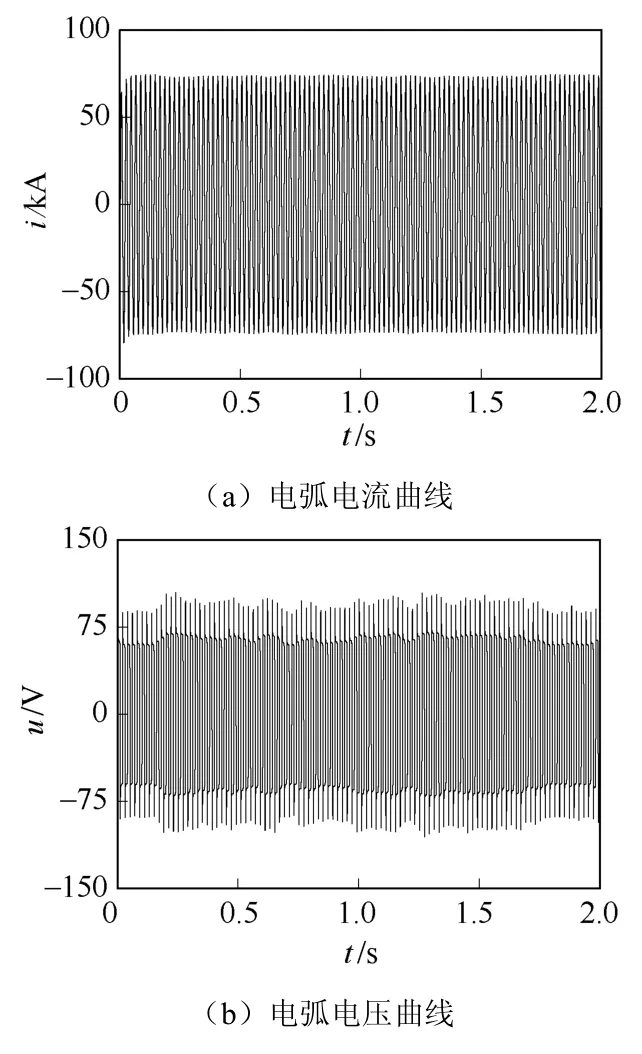
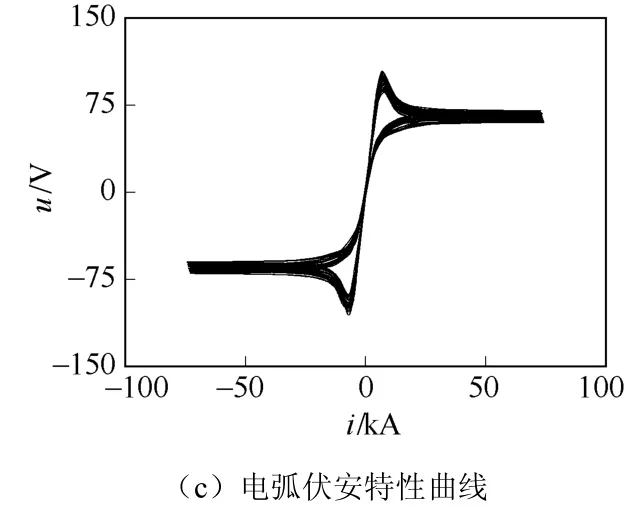
图6 精炼期电弧炉的动态特性

图7 精炼期35kV母线A相电压曲线
通过表2可以观察到,精炼期的谐波电流较熔化期大幅下降,特别是5次和7次谐波,已降至国标允许值以下,电弧炉在精炼期对电网的污染较小,仿真结果与实际相吻合。
3 结论
本文提出了一种基于能量守恒定律,以电弧导纳为状态变量,电弧电流和弧长作为输入的交流电弧炉模型,创新地采用随弧长连续随机变化的模型参数Uarc(L)和k(L),并给出了相应的工程估算方法,两者均与弧长相关,有明确的物理意义。分别对熔化期和精炼期的电弧炉特性以及电网电压波动和谐波进行了仿真分析,仿真结果与实测数据对比表明,该模型能够准确地模拟不同冶炼时期电弧炉的动态特性以及造成的电网电压波动和谐波污染。
本文提出的时变参数模型区别于以往的从能量平衡关系出发或基于实测数据建立的模型。一是可以通过时刻变化的参数精确地模拟电弧炉在不同运行阶段的动态特性,避免了采用固定参数来仿真时变系统的不足;二是只需电弧炉系统的初始设计参数就可以实现模型的仿真,从而并不仅仅针对特定的电弧炉,因此具有准确性和普适性。该模型适用于预测和评估电弧炉接入电网后可能引发的电能质量问题,以便提前采取相应的治理措施,具有一定的工程应用价值。
[1] 彭卉,邹舒,付永生,等. 冲击负荷接入电网的电能质量分析与治理方案研究[J]. 电力系统保护与控制,2014,42(1)︰54-61.
[2] 金维刚,刘会金,李智敏,等. 3种典型间谐波源的间谐波测量及结果分析[J]. 电力自动化设备,2010,30(12)︰30-35.
[3] 刘书铭,李琼林,陈栋新,等. 中高压配电网非线性用户的电能质量特性研究[J]. 电力系统保护与控制,2012,40(15)︰150-155.
[4] 鞠平,王耀,项丽,等. 考虑特殊负荷的宁夏电网负荷建模[J]. 电力自动化设备,2012,32(8)︰1-4,21.
[5] 王育飞,姜建国. 用于电能质量研究的新型交流电弧炉混沌模型[J]. 中国电机工程学报,2008,28(10)︰106-110.
[6] Alonso M P,Donsion M P. An improved time domain arc furnace model for harmonic analysis[J]. IEEE Transactions on Power Delivery,2004,19(1)︰367-373.
[7] Montanari G C,Loggini M,Cavallini A,et al. ARC-FURNACE MODEL FOR THE STUDY OF FLICKER COMPENSATION IN ELECTRICAL NETWORKS[J]. IEEE Transactions on Power Delivery,1994,9(4)︰2026-2036.
[8] Acha E,Semlyen A,Rajakovic N. A HARMONIC DOMAIN COMPUTATIONAL PACKAGE FOR NONLINEAR PROBLEMS AND ITS APPLICATION TO ELECTRIC-ARCS[J]. IEEE Transactions on Power Delivery,1990,5(3)︰1390-1397.
[9] 池伟,张恺伦,查蕾,等. 基于能量平衡的电弧炉模型的仿真与参数辨识[J]. 机电工程,2012,29(4)︰454-457.
[10] 王晶,束洪春,林敏,等. 用于动态电能质量分析的交流电弧炉的建模与仿真[J]. 电工技术学报,2003,18(3)︰53-58.
[11] Wang Yan,Mao Zhizhong,Tian Huixin,et al. Modeling of electrode system for three-phase electric arc furnace[J]. Journal of Central South University of Technology,2010,17(3)︰560-565.
[12] 刘小河,赵刚,于娟娟. 电弧炉非线性特性对供电网影响的仿真研究[J]. 中国电机工程学报,2004,24(6)︰30-34.
[13] 陈大宣,余一平,鞠平,等. 基于时变电流注入方法的特殊电力负荷建模研究[J]. 电力自动化设备,2014,34(3)︰120-124.
[14] Chang Gw,Min-Fu S,Chen Yiying,et al. A hybrid wavelet transform and neural-network-based approach for modelling dynamic voltage-current characteristics of electric arc furnace[J]. IEEE Transactions on Power Delivery,2014,29(2)︰815-824.
[15] 王其平. 电器电弧理论[M]. 北京︰机械工业出版社,1982.
[16] 王丰华. 电弧炉建模研究及其应用[D]. 上海︰上海交通大学,2006.
[17] Paschkis,Persson. Industrial electric furnaces and appliances[M]. new york︰interscience publishers,1960.
[18] (日) 南条敏夫,李中祥. 炼钢电弧炉设备与高效益运行[M]. 北京︰冶金工业出版社,2000.
[19] Manchur G,Erven CC. Development of a model for predicting flicker from electric arc furnaces[J]. IEEE Transactions on Power Delivery,1992,7(1)︰416-426.
[20] 仝永博,刘征,罗玉镯,等. 采用长弧操作的高阻抗电弧炉[J]. 冶金设备,2014(6)︰20-24.
Time-varying Parameter Model of AC Electrical Arc Furnace for Power Quality Predictions and Analysis
Liao Yantao1Hu Jun1Zhang Hailong2Wang Enrong1
(1. College of Electrical and Automation Engineering,Nanjing Normal University,Nanjing210042;2. College of Physics and Technology,Nanjing Normal University,Nanjing210023)
A novel time domain differential model is proposed for the AC EAF (Electrical Arc Furnace) based on the law of conservation of energy. The model is established with arc admittance as a state variable,and with arc current and arc length as the input. The relation between the parameters with arc length is derived from the formula of the arc length and voltage. The engineering estimation method of time-varying parameters are further realized. Moreover,the limited bandwidth random signal is added on the arc length,and actual working state was simulated. A real EAF is taken to simulate the dynamic characteristics as well as the grid voltage fluctuation and harmonic wave in melting and refining stages. The results coincide with the measured data so prove the validity and practicability of the model.
electrical arc furnace;arc impedance;time-varying parameter;power quality;load modeling
廖延涛(1990-),男,安徽淮南人,硕士研究生,主要从事电力系统冲击负荷电能质量分析与治理。
国家自然科学基金项目(51475246)
江苏省普通高校研究生科研创新计划项目(KYLX15_0725)
