基于非负矩阵分解的半监督动态社团检测

常振超，陈鸿昶，黄瑞阳，于洪涛，刘阳



基于非负矩阵分解的半监督动态社团检测

常振超，陈鸿昶，黄瑞阳，于洪涛，刘阳

（国家数字交换系统工程技术研究中心，河南郑州 450002）

如何有效融合不同时刻的网络结构信息，是影响复杂网络中动态社团检测算法检测性能的关键和难点。基于此，提出了一种基于非负矩阵分解的半监督动态社团检测方法SDCD-NMF，该方法首先有效提取了历史时刻所包含的稳定结构单元，然后将其作为正则化监督项，指导当前时刻的网络社团检测。在真实网络数据集上的实验表明，所提方法与已有方法相比具备更高的社团划分质量，更有利于探索网络的演变与发展规律。

半监督；动态；社团检测；非负矩阵分解

1 引言

网络涵盖人类生活的方方面面，对网络中的社团进行挖掘一直是跨各学科领域研究者所共同关注的热点。社团是密集交互的群组，如社会网络中具备相同爱好或者属性特征的群体、生物网络组织中的器官、科学家合作网络中相同领域的研究小组等[1]。网络通常用图来进行表示，图中节点表示网络中的基本构建单元，链接表示节点之间的交互。已有的经典算法诸如基于连接的GN算法[2]、图谱分析方法[3]、非负矩阵分解方法[4]等大多从基于静态网络分析[5~7]角度出发。而许多真实的网络是持续演化的[8]，即网络结构随着时间刻度不断变化，对静态分析算法有必要进行进一步地扩展，以适应动态网络分析的需求。动态社团检测[9]就是从这种变化的网络结构中检测不同时间刻度上密集连接的群组。从静态网络分析转向对动态网络的演化研究是近年来复杂网络研究的新趋势。

已有大量针对动态网络的社团检测的方法被研究者提出，主要可以分为2类[10,11]：一类是基于进化聚类的方式，该方法依据动态网络变化缓慢的基本特征，在对每个时刻的网络进行聚类时，既要使聚类结果与当前时刻的网络结构（静态快照质量）尽量一致，又要满足当前聚类结果与历史时刻的网络结构差异较小（历史开销）；另一类是基于增量聚类的方法，增量的方法以历史时刻网络划分为基础，仅针对增量相关的节点和边进行处理，算法运算速度较快，但为减少时间上的花费，一般都会对聚类质量造成一些牺牲，难以有效应对社团数目发生变化等情况。非负矩阵分解(NMF, non- negative matrix factorization)作为一种有效的高维数据降维方法，具备非负性和易解释性，在数据挖掘领域中得到了广泛应用[12]。由于能够从本质上揭示图数据网络的基本组成，研究者们将其成功地运用在社团检测领域中。基于图正则化的半监督非负矩阵分解方法，将约束信息（部分节点连接信息）指导分解迭代过程中，能够有效提升算法的准确性，在文本聚类、图数据挖掘和静态社团检测等领域已经取得了较大的研究进展[4, 13~17]。

基于上述分析，本文从提升动态网络社团检测精度的角度出发，采用进化聚类的方式对其展开研究，即如何高效地利用历史时刻的信息指导当前时刻的网络划分，提出了一种基于非负矩阵分解的半监督动态社团检测方法SDCD-NMF，该方法首先有效提取了历史时刻所包含的稳定结构信息，然后将其作为非负矩阵分解的正则化项，指导当前时刻的网络社团检测。本文所提方法首次将半监督的非负矩阵分解架构应用到动态社团检测中去，其优势在于有效提取并融合了历史时刻的约束信息，指导当前时刻的社团划分，为动态网络社团检测提供了新的研究思路和框架。

2 相关工作

真实的网络不断演化，其社团结构随着时间推进也在发生变化，例如社团中节点和连边的消失和增加、社团的合并和分类等。针对动态变化的网络社团挖掘仍处于起步阶段。近几年来，国内外研究者分别针对社团的演化提出了一些不同的模型和方法，主要可以分为2类：增量聚类和进化聚类。下面对这2类方法相关研究进展进行了简要回顾。

2.1 基于增量聚类的动态社团检测

基于增量聚类的动态社团检测是一种动态更新策略，将历史时刻的社团划分作为基础，在后续阶段进行更新，大多从增量相关的节点和边出发进行研究，算法的运算效率较高。如Sun等[18]提出的基于信息论的GrapScope算法，以增量的方式选择信息编码花费最小的方式进行划分。黄永锋等[19]提出了一种基于社会特征周期演化的社团检测方法，用之服务于网络路由转发策略的设计。Ning等[20]提出了一种增量谱聚类的方法，通过引入发生矩阵来描述网络节点的增、删以及节点相似性变化，增量更新谱系统。单波等[21]提出了一种增量IC算法，该算法基于社团数目是恒定不变的。肖杰斌等[22]提出了一种随机游走的增量处理相关节点的方法，对增量相关节点进行随机游走聚类，扩展了算法的适用性。郭进时等[23]将拓扑势引入到增量相关节点的处理上去，一定程度上提高了算法的检测精度。Miguel等[24]提出了一种基于张量分析的增量识别算法，将张量分解与异常检测相融合，通过对不同张量的迭代分析，以获取增量节点的社团归属。另外，也有其他将经典算法进行改进为增量聚类方法，如本征矢量分解方法[25]、Rober[26]提出的切割数方法和Duan等[27]提出的派系图方法等。

2.2 基于进化聚类的动态社团检测

进化聚类通常假设历史信息具备时域平滑性，即当前时刻的社团划分同前一时刻社团划分结果相差不大。Chakrabarti等[9]最早提出了一种进化聚类分析架构，该方法将当前时刻动态社团划分结果看成是当前时刻的静态快照划分质量与历史时刻社团划分结果的折中，既要满足静态划分的拓扑一致性，也要使历史开销尽量小，即一个好的社团划分结果也能够尽量满足前一时刻的网络基本结构，其划分质量可以用下述公式来进行描述。

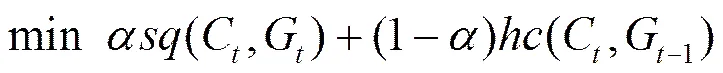
2.3 已有算法分析

基于增量聚类的动态社团检测，以历史时刻所获取的社团划分为基础，然后进行增量相关部分调整，大多假设社团的数目不发生变化，难以有效应对社团的合并、分裂和消亡等数目变化情况，虽然通常具备较高的运算效率，但一般都会对聚类质量造成一些牺牲，导致其算法精度有待提升。而基于进化聚类的动态社团检测，从不同时刻的检测结果进行综合考虑，将历史信息融入到社团检测中来，利用历史有效信息减少噪声的影响，优化了当前时刻的社团划分，能够取得较好的检测效果，由于其能够检测社团中社团数目变化，具备更好的适应动态社团检测需求，拥有更好的检测性能和合理的动态网络解释性，但如何有效利用历史信息是进化聚类算法的关键。

综上所述，本文从提升动态网络社团检测精度的角度出发，采用进化聚类的方式展开研究，提出了一种基于非负矩阵分解的半监督动态社团检测方法。该方法首先提取历史信息中所包含的稳定连接关系，然后将其作为约束项以指导当前时刻的划分，采用了半监督的非负矩阵分解架构，克服了线性融合不同时刻的社团划分需要人工设定平衡因子的缺陷，有效融合了历史信息，具备更好的理论基础和可行性。

3 半监督动态社团检测

传统的进化聚类大多采用线性组合不同时刻社团划分结果的方法，即将历史划分开销和静态快照质量开销进行线性优化，需要确定这两者之间的平衡因子，但该因子通常是人工进行设定，缺乏有效的优化策略，如何有效融合历史信息是进化聚类算法性能提升的关键。本文采用半监督的非负矩阵对社团进行划分，首先将历史时刻的稳定连接关系进行提取，作为约束信息（图正则化项）进而指导当前时刻的网络划分，以克服原有算法中需要人工确定平衡因子的缺陷，能够有效提升动态社团的检测精度。

3.1 相关定义及分析

3.2 非负矩阵分解

由于网络节点间的链接总是非负的，即边权重都是非负的，因此，非常适合采用非负矩阵分解进行社团检测[4~8]。基于非负矩阵进行社团检测的基本定义如下，假设拥有个节点的某网络的邻接矩阵为，则NMF定义为：通过寻找最大近似原始网络数据的2个低秩因子矩阵和来实现社区发现，分解后得到的基向量矩阵表示网络降维后的社区特征，具有稀疏性和线性无关性，而归属矩阵则表示相应节点与社区的隶属程度。其一般采用欧几里德距离最小化方式，优化的目标函数为

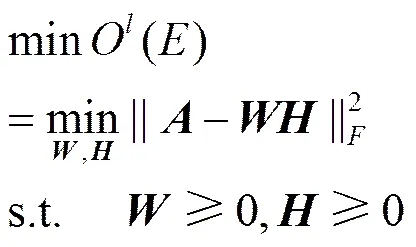
3.3 约束信息获取

因此，这里半监督信息主要关注成对约束信息，即同一条边所连接的2个节点是否属于同一个社团情况。成对约束主要包括2种信息，即must-link和cannot-link，而这里只关注must-link，原因是该约束主要用于控制数据压缩之后表示的距离更近；而cannot-link表示不同类别之间的相似度，且在本文中难以进行有效的提取。对must-link信息进行介绍如下。

现在问题转化为如何有效提取历史时刻的约束信息上，动态网络一般采用时间刻度分析方法，已经有大量的提取共有特征的方法，本文采用挖掘历史时刻稳定的微观结构—三角结构，来确定节点之间的成对约束关系。相关研究表明[37,38]，三角结构是网络中较为稳定的结构关系，借助三角结构信息挖掘社团已经有了大量的相关研究。即便出现社团消亡、分裂情况，稳定三角结构中包含的成对约束在不同的相邻时刻里，仍然能够以较大概率满足成对约束，其不对具体的聚类标示进行修改，而只是表明了节点处于同一个社团的可能性较大，更能符合社团数目变化或者节点对社团归属改变的情况，更具备理论指导意义。对三角结构信息的稳定性结合图2进行分析如下。

在图2的三角结构中，、和分别为其3个顶点，当前时刻该三角结构满足三角结构，设定下一时刻该三角结构中任何一条边（连接）断掉，即不再满足must-link的成对约束的概率为，则仍保持图2(a)三角结构的概率为，跳变为图2(b)只有一条边（连接）断掉的概率为，跳变为图2(c)断掉2条边（连接）的概率为，3条边（连接）完全断掉即跳变为图2(d)的概率为。至此，所有成对约束边跳转情况分析已经结束。

1) must-link约束：即下一时刻为图2(a)时，3个节点中两两满足仍为成对约束情况。

2) must-link约束传递：即下一时刻为图2(b)时，通过2个边的连接扩展，补充到第3条边的连接情况，即满足成对约束的传递性。

综上所述，在历史时刻中三角结构中的顶点，在当前时刻仍处于同一个社团的概率为，此概率值接近于1。原因如下，进化聚类假设相邻时刻的网络结构不会出现剧烈的变化，即变化部分占据了很小的比例，体现在微观的连边在下一时刻断掉的概率值很小，其出现图2(a)和图2(b)的概率较高，即在当前时刻3个节点仍两两近似满足成对约束。同时，在本文实验中也验证了采用三角结构来对历史稳定信息进行刻画的有效性。

对三角结构作为历史监督信息有效性分析之后，约束信息获取过程的描述如下所示。

2) 由三角结构的顶点关系，根据定义3，构造两两节点之间的成对约束矩阵。

3.4 基于图正则化的非负矩阵分解方法

本节将给出本文所提出半监督动态检测方法，这里采用基于图正则化的非负矩阵分解方法，由于其能够有效利用部分节点的先验信息，已经在很多领域得到了成功的应用[4~8]。该方法基于流行假设，即对原始数据图矩阵进行分解之后，在得到的特征矩阵空间上（变换空间后），同一类节点之间的距离更近，而不同类节点之间的距离更远，改进后的半监督方法的优化目标为

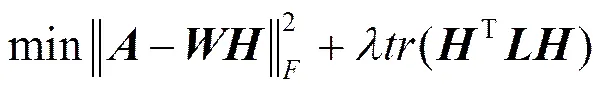
根据基于图正则化项的半监督NMF求解优化过程[4]，对于原式中的矩阵和进行求解，为保证求解过程的非凸性，对参数进行分别更新，此优化问题的迭代过程如下所示。

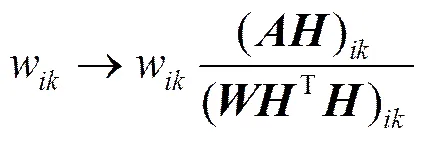
(5)

当相邻2次迭代过程中，目标函数差值满足较小(通常设定为10−5)，或其值不再变小时，算法收敛，迭代过程终止。

基于最终的优化目标函数和历史时刻网络，对本文所提基于非负矩阵分解的半监督动态社团检测具体步骤进行描述如下。假设需要计算时刻的网络社团划分结构，已知时刻到的网络结构。首先，基于NMF算法，提取时刻网络中的社团结构；然后，根据，提取出社团结构中包含的三角结构，构造时刻的成对约束先验信息；最后，根据式(3)，采用基于图的正则化方法，计算时刻社团结构，依次类推，直到计算出所需要的时刻的社团归属矩阵。本文所提方法，按照时刻不同，提取出不同的稳定历史结构信息，在同一个非负矩阵分解框架下，能够有效利用历史信息中包含的约束信息，进而指导当前时刻的社团检测。

算法2 融合多属性算法

5) while not convergent do

8) end while

9) end for

在算法2中，首先经过初始化矩阵，通过前一时刻的网络社团中约束信息获取，指导当前时刻的社团划分，矩阵运算过程中，固定其中2个变量，然后反复迭代运算，直到目标函数收敛，以求得和。

3.5 模型选择

在动态网络中，需要确定每个时刻上不同的社团数目，这就是模型选择问题，即确定社团检测中的社团数目，也就是在矩阵分解迭代运算中矩阵的行数。已经有很多种模型选择方法提出来[17,24,25]，有基于本征值差异方法[39]、交叉验证贝叶斯方法[7,40]和基于模块度的方法[5,6]等。需要提前对社团数目进行预估计。本文采用文献[41]所采用谱分析的方法，该方法基于裴龙聚类(Perron clusters)的本征值所决定[42]。

由于本文基于链接矩阵作为基矩阵进行估计，社团数目可由该链接矩阵的谱分析进行预估计。首先构造对角方阵，该方阵中的对角线上的值为图中相应节点度（链接个数）的大小。基于这2个矩阵构造拉普拉斯矩阵，并对其进行正规化，获取正规化矩阵。

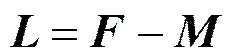
(6)

本文所提模型选择方法用于提前确立不同时刻网络结构中的社团数目，其独立于社团检测过程。

3.6 复杂度分析

本文设计的动态社团检测算法复杂度主要考虑3个方面：约束信息的获取、模型选择和半监督的矩阵迭代分解。假定网络节点个数为，网络社团数目为，在约束信息获取过程中，需要提取已知社团结构中的三角形，且三角形结构中存在节点重叠现象，取不同的社团中节点数目相等进行计算，且社团中所有节点均为全连接情况，其算法复杂度为，在实际情况中，社团内部不可能所有的节点满足全连接这个假设，因此，复杂度应远小于。模型选择中裴龙聚类包含对角矩阵获取、规范化和本征特征值的计算，这3个步骤中，复杂度最高的为本征值获取，按照最高的运算复杂度进行取值，其算法复杂度为。半监督的矩阵分解中，算法复杂度除了矩阵乘运算之外，还取决于迭代次数。其算法复杂度约为，当考虑矩阵的稀疏程度时，该值可以进一步降低为，其中，是must-link的先验信息中节点对个数，是矩阵中数值为1的个数，即真实存在的边个数。综合三者分析，本文设计算法的复杂度最大约为++。

4 实验

为验证本文所提算法的有效性，本文在真实网络数据集上进行了相关的实验，并对实验结果进行了分析。

4.1 实验数据

对已有文献中所广泛应用的网络仿真数据集进行分析，选择了2类数据库进行验证：一类是全局背景已知的情况，采用的是常见的网络仿真数据库工具LFR进行生成人工网络；另一类是3种常见的真实网络数据库。3种最常见的数据集进行了仿真实验，包括Enron邮件网络[43]、arXiv电子引文网络[44]和Facebook社交网络[45]。这些网络数据集覆盖了一定的时间间隔，借鉴文献[46]中的实验数据的静态图构建方式，对数据进行提炼，以构造有效的数据集，本文所采用的相应数据库具体介绍如下。

LFR网络[43]：本文中LFR网络参考文献[30]的实验设置，生成网络数目为50个，且在相同的参数设置下，产生10个网络静态图。仿真了节点个数为10 000情况下，混合参数为0.3和0.5的情况。

Enron邮件网络[44]：该网络包含了150个用户之间的邮件信息，是Enron公司高级管理人员之间的通信。时间为1999年1月~2012年8月。对原始数据进行提炼，挑选其中7个主要的社团，其连接数大约占了总连接数目的50%，按照社团的生长过程，当连接数目变化大约为1 000条连接时构建新的快照，总共构建了21个生长型网络快照，即21个时间刻度。

arXiv电子引文网络[45]：本文采用的数据库为1996年1月~2003年5月，在本文的实验中，对最初的1996年~1997年数据中所包含的网络数据进行获取初始社团结构。采用1998年1月~2003年1月之间的数据，按照2个月时间间隔，构建了30个静态图，即30个时间刻度。

Facebook社交网络[47]：该数据集包含了Facebook网络中新奥尔良区域内注册用户之间的朋友关系，时间为2006年9月~2009年1月。数据集包含了6万个节点，150万个连接关系。本文中数据采用2006年9月~2006年12月的数据作为原始网络数据。按照时间刻度每个月构造静态图。从2007年1月~2009年1月总共构造25张静态图，即25个时间刻度。

4.2 对比算法

为全面分析比较本文所提算法的性能，实验挑选3类具备代表性的对比算法。1）NMF[12]，仅针对静态图的进行社团发现，该方法是一种无监督聚类的方法，由于本文是采用历史信息作为半监督信息的NMF方法，故选择仅对静态图进行社团挖掘的NMF方法作为对比算法。2）FaceNet[29]，该方法基于生成模型进行演化分析，首次将矩阵分解应用到此类问题中来，其针对历史时刻和当前时刻分别进行联合估计获取社团划分，采用平衡因子将两者划分进行统一，取得了较好的效果，是常用于对比算法中的经典算法。3）A3CS[30]，该方法是动态社团检测中提出较新的算法，其从保证模块度最大化的角度出发，取得了较好的识别效果和较高的算法运行效率。

4.3 评价指标

在本文实验数据中，针对网络的真实社团划分已知和未知的情况，需要采用不同的社团划分评价指标。因此，本文实验中选取常用的测试指标归一化互信息指标NMI[43]和模块度[1]来测试社团检测性能。NMI用于衡量已知社团结构下，检测出来的社团结构与已知社团结构的差异程度，NMI值越大，划分结果与已知的社团结果越相似。模块度是由Newman和Girvan提出的一种用于评价划分结果的重要指标，该指标通过与随机网络的差异程度，来衡量发现所发现网络社团的模块化程度，即网络的社团化程度越高，社团结构越明显，其值越大，相应地，通常认为社团检测算法性能越好。同时，为对算法的效率进行分析，对真实网络数据集上的运行时间，也进行了实验分析。

4.4 实验结果

1) LFR邮件网络

在LFR人工网络数据集上进行实验，结果如图3所示。由图3(a)可知，本文所提的方法获得了较高的NMI取值，且在不同的时刻，该值保持的比较稳定。与其余3种算法相比，性能与A3CS大致相当，但仍在大部分时刻取得了一定的优势，这说明了本文所提的方法更为准确地挖掘不同时刻的社团结构，验证了算法的有效性。在图3(b）中，随着混合参数的增加，网络结构更为复杂，所有算法均出现了一定程度的检测性能的降低，而本文所提方法仍能够保持较高的NMI取值，即较好的检测性能。说明了算法在针对更为复杂的网络结构时，仍能够使用。

2) Enron邮件网络

在Enron网络数据集上进行实验，结果如图4所示。由图4(a)可知，在对Enron邮件网络进行仿真时，随着时间间隔的增加，本文所提算法SCD-NMF，相比于其他3种方法，均取得了较高的值，其中，仅对静态图进行社团检测的方法，由于缺少相关的监督信息，值最小，因此，本文算法更能适应网络的动态变化，更能有效挖掘网络中存在的社团结构信息。同时，邮件网络的值较低，说明了该网络的社团结构化不是很明显。由图4(b)可知，随着网络规模的增大，本文所提的方法在运行时间上仅略高于A3CS方法，但要极大地低于其他2种基于矩阵分解的方法FaceNet和NMF，且随着网络规模的增加，算法的运行时间增加并不多。原因在于，基于NMF的社团发现，在算法运行时间上与单次迭代的时间和迭代次数相关，本文所提方法，由于结合了历史监督信息，极大地减少了算法的迭代次数，加快了算法收敛性，减少了运行时间。因此，算法运行效率较高。

3) arXiv电子引文网络

在arXiv网络数据集上进行实验，结果如图5所示。由图5(a)可知，在对arXiv电子引文网络进行仿真时，本文所提算法SCD-NMF，相比于其他3种方法，也同样均取得了较高的值，其中仅对静态图进行社团检测的方法，由于缺少相关的监督信息，值下降的最为厉害，分析可知，随着网络规模的急速增加，网络的社团结构化越不明显，此时，仅仅依靠对单个静态图的分析，难以有效反映社团结构的变化。同时，算法在电子引文网络上的值较高，说明了该网络的社团结构化较为明显。由图5(b)可知，本文所提的方法在运行时间上仅略高于A3CS方法，但要极大地低于其他2种基于矩阵分解的方法FaceNet和NMF，且随着网络规模的增加，算法的运行时间增加并不多，原因在图4(b)的分析中已经给出，验证了利用历史信息，能够有效地减少迭代次数，提高了算法运行效率。

4) Facebook社交网络

在Facebook网络数据集上进行实验，结果如图6所示。由图6(a)可知，由于本文社团检测时，采用已知的账户进行采集数据，其Facebook社交网络更具备社团化结构，因此，随着朋友的不断加入，其值呈增加状态。在不同的时刻上进行仿真可知，本文所提算法SCD-NMF，相比于其他3种方法，均取得了较高的值，且相比其他算法，本文所取得值增加幅度很大，原因在于，Facebook社交网络的历史信息起了很大的指导作用，即前一时刻的网络连接——朋友信息，一般会保持下去，不会出现剧烈的断连接情况，但其网络变化仍剧烈，因为社团规模不断增加，因此，其他3种方法取得的效果增加率小于本文所提算法。同时，由图6(b)可知，本文所提的方法也具备了较高的运行效率，原因见图3(b)的详细分析。

5 结束语

本文从提升动态网络社团检测性能的角度出发，提出了一种基于非负矩阵分解的半监督动态社团检测方法SDCD-NMF，并通过真实网络上的实验验证了本文的有效性。该方法有效提取了历史时刻的网络信息，并将其在同一个社团检测架构中进行融合分析，为动态网络社团检测提供了新的研究思路和框架，更有利于深入探索网络的演变与发展规律。此外，动态变化的社会网络，为社团检测提供了更大规模和更多异构的信息源（不同的链接关系、不同的节点属性和多种信息来源等），如何有效应对这种“异质多源”的海量动态媒体数据，进而挖掘其中存在的社团结构，将是下一步工作的研究重点。

[1] FORTUNATO S. Community detection in graphs[J]. Physics Reports, 2010,486(3-5):75-174.

[2] GIRVAN M, NEWMAN M E J. Community structure in social and biological networks[J]. Proc Natl Acad Sci, 2002, 99 (2002)：7821-7826.

[3] LUXBURG U. A tutorial on spectral clustering[J]. Statistics and Computing, 2007, 17(4):395-416.

[4] YANG L, CAO X C, JIN D. A unified semi-supervised community detection framework using latent space graph regularization[J]. IEEE Transactions on Cybernetics, to Appear 2015, DOI: 10. 1109/TCYB. 2014. 2377154.

[5] ZHANG Z Y. Community structure detection in complex networks withpartial background information[J]. Europhys Lett, 2013, 101(4): Art. ID 48005.

[6] 郭昆, 郭文忠, 邱启荣, 等. 基于局部近邻传播及用户特征的社区识别算法[J]. 通信学报,2015, 36(2):2015035-1—2015035-12.

GUO K, GUO W Z, QIU Q R, et al. Community detection algorithm based on local affinity propagation and user profile[J]. Journal of Communications, 2015, 36(2):2015035-1—2015035-12.

[7] 卫红权, 陈鸿昶, 刘力雄, 等. 基于强度排序的通信社区检测算法[J]. 通信学报, 2014, 35(10): 165-170.

WEI H Q, CHEN H Q, LIU L X, et al. Communication community detection algorithm based on ranking of strength[J]. Journal of Communications, 2014, 35(10): 165-170.

[8] EUSTACE J, WANG X Y, CUI Y Z, et al. Overlapping community detection using neighborhood ratio matrix[J]. Physica A, 2015, 421(2015): 510-521.

[9] CHAKRABARTI D, KUMAR R, TOMKINS A S, et al. Evolutionary clustering[C]//The 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. c2006:554-560.

[10] CAZABET R, AMBLARD F. Dynamic community detection[M]. Encyclopedia of Social Network Analysis and Mining. Springer New York Press, 2014.

[11] CHARU A, KARTHIK S. Evolving network analysis: a survey[J]. ACM Computing Surveys, 2014, 47(1):1-36.

[12] LEE D D, SEUNG H S. Learning the parts of objects by non-negative matrix factorization[J]. Nature, 1999, 401(6755): 788-791

[13] LAI J H, WANG C D, YU P. Dynamic community detection in weighted graph streams[C]//The 2013 SIAM International Conference on Data Mining, c2013:151-161.

[14] CHENG Y, REGE M, DONG M, et al. Non-negative matrix factorization for semi-supervised data clustering[J]. Knowledge and Information Systems, 2008, 17(3): 355-379

[15] WANG H, NIE F P, HUANG H. Nonnegative matrix tri-factorization based high-order co-clustering and its fast implementation[C]// The 2011 SIAM International Conference on Data Mining. c2011: 774- 783.

[16] 尚凡华. 基于低秩结构学习数据表示[D]. 西安: 西安电子科技大学, 2012.

SHANG F H. The low rank structure learning based on data representation[D]. Xi’an: Xidian University, 2012.

[17] CAI D, HE X F, HAN J W, et al. Graph regularized non-negative matrix factorization for data representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 8(33): 1548-1560.

[18] SUN J M, PAPADIMITRIOU S, YU P S, et al. Graphscope: parameter-free mining of large time-evolving graphs[C]//The 13th ACM SIGKDD Int’l Conf on Knowledge Discovery and Data Mining. c2007: 687-696.

[19] 黄永锋, 董永强, 张三峰, 等. 基于社会特征周期演化的机会移动网络路由转发策略[J]. 通信学报, 2015, 36(3): 2015055.

HUANG Y F, DONG Y Q, ZHANG S F, et al. Message forwarding based on periodically evolving social characteristics in opportunistic mobile networks[J]. Journal of Communications, 2015, 36(3): 2015055-1—2015055-12.

[20] NING H Z, XU W, CHI Y, et al. Incremental spectral clustering by efficiently updating the eigen-system[J]. Pattern Recognition, 2010, 43(1):113-127.

[21] 单波, 姜守旭, 张硕. IC: 动态社会关系网络社区结构的增量识别算法[J]. 软件学报, 2009, 20(1): 184-192.

SHAN B, JINAG S X, ZHANG S. IC: incrementalalgorithm for community identification in dynamic socialnetworks[J]. Journal of Software, 2009, 20(1):184-192.

[22] 肖杰斌, 张绍武. 基于随机游走和增量相关节点的动态网络社团挖掘算法[J]. 电子与信息学报, 2013, 35(4):977-981.

XIAO J B, ZHANG S W. An algorithm of integrating random walk and increment correlative vertexes for mining community of dynamic networks[J]. Journal of Electronics & Information Technology, 2013, 35(4):977-981.

[23] 郭进时, 汤红波, 王晓雷.基于社会网络增量的动态社区组织探测[J]. 电子与信息学报, 2013, 35(9): 2240-2246.

GUO J S, TANG H B, WANG X L. A dynamic community structure detection scheme based on social network incremental[J]. Journal of Electronics & Information Technology, 2013, 35(9): 2240-2246.

[24] MIGUEL A, SPIROS P, STEPHAN G, et al. 1Com2: fast automatic discovery of temporal ('Comet') communities[C]//The PAKDD. c2014:271-283.

[25] NIGN H Z, XU W, CHI Y, et al. Incremental spectral clustering with application to monitoring of evolving blog communities[C]//The 2007 SIAM International Conference on Data Mining. c2007: 261-272.

[26] ROBERT G, TANJA H, DOROTHEA W. Dynamic graph clustering using minimum-cut trees[J]. Journal of Graph Algorithms and Applications, 2012, 16(2):411-446.

[27] DUAN D S, LI Y H, LI R X, et al. Incremental-clique clustering in dynamic social networks[J]. Artificial Intelligence, 2012, 38(2): 129-147.

[28] CHI Y, SONG X D, ZHOU D Y, et al. Evolutionary spectral clustering by incorporating temporal smoothness[C]//The 13th ACM International Conference on Knowledge Discovery and Data Mining. c2007: 153-162.

[29] LIN Y R, CHI Y, ZHU S H, et al. Analyzing communities and their evolutions in dynamic social networks[J]. ACM Transactions on Knowledge Discovery from Data, 2009, 3(2):8:1-8:31.

[30] THANG N D, NGUYEN N P, THAI M T. An adaptive approximation algorithm for community detection in dynamic scale-free networks[C]//The 2013 IEEE INFOCOM. c2013: 55-59.

[31] GORKE R, MAILLARD P, SCHUMM A, et al. Dynamic graph clustering combining modularity and smoothness[J]. ACM Journal of Experimental Algorithmics, 2013, 18(1):1.5:1.1-1.5:1.29.

[32] BECCHETTI L, BOLDI P, CASTILLLO C, et al. Efficient semi- streaming algorithms for local triangle counting in massive graphs[C]// The 14th ACM SIGKDD international conference on Knowledge discovery and data mining. c2008:16-24.

[33] KIM M S, HAN J W. A particle-and-density based evolutionary clustering method for dynamic networks[C]//The 35th International Conference on Very Large Databases. c2009:622-633.

[34] TANG L, LIU H, ZHANG J P. Identifying evolving groups in dynamic multimode networks[J]. IEEE Trans on Knowledge and Data Engineering, 2012, 24(1):72−85.

[35] XU KS, KLIGER M, HERO A O. Adaptive evolutionary clustering[J]. Data Mining and Knowledge Discover, 2014, 28(2): 304-336.

[36] MA H F, ZHAO W Z, SHI Z Z. A nonnegative matrix factorization framework for semi-supervised document clustering with dual constraints[J]. Knowledge and Information Systems September, 2013, 36(3):629-651.

[37] WASSERMAN S, FAUST K. Social network analysis: methods and applications[M]. Cambridge University Press, 1994.

[38] PALLA G, DETRNYI I, FARKAS I, et al. Uncovering the overlapping community structure of complex networks in nature and society[J]. Nature, 2005, 435(1):814-818.

[39] NEWMAN M. Spectral methods for network community detection and graph partitioning[J]. Phys Rev E, 2013, 88(4):042822:1-042822:11.

[40] AIROLDI E M, BLEI D M, FIENBERG S E, et al. Mixed membership stochastic block models[J]. J Mach Learn Res, 2009, 9(1):1981-2014.

[41] CHRISTOPHER M, MAES. A regularized active-set method roe sparse convex quadratic programming[M]. 2010 Ph D Dissertation Stanford university.

[42] WEBER M, RUNGSARITYOTIN W, SCHLIEP A. Perron cluster analysis and its connection to graph partitioning for noisy data[M]. Konrad-Zuse-Zentrum für Informationstechnik Berlin, 2004.

[43] LANCICHINETTI A, FORTUNATO S. Community detection algorithms: a comparative analysis[J].Phys Rev E 2009, 80(5):733-737.

[44] SUN J, FALOUTSOS C, PAPADIMITRIOU S, et al. Graphscope: parameter-free mining of large time-evolving graphs[C]//The 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. c2007:687-696.

[45] ArXiv dataset[EB/OL]. http://www.cs.cornell.edu/projects/kddcup/ datasets.html. 2003.

[46] NGUYEN N P, DINH T N, XUAN Y, et al. Adaptive algorithms for detecting community structure in dynamic social networks[C]//The 2011 INFOCOM. c2011:2282-2290.

[47] VISWANATH B, MISLOVE A, CHA M, et al. On the evolution of user interaction in facebook[C]//The 2nd ACM workshop on Online social networks. c2009:37-42.

Semi-supervised dynamic community detection based on non-negative matrix factorization

CHANG Zhen-chao, CHEN Hong-chang, HUANG Rui-yang, YU Hong-tao, LIU Yang

(National Digital Switching System Engineering & Technological Research Center, Zhengzhou 450002, China)

How to effectively combine the network structures on different time points was the key and difficulty to affect the performance of detection algorithms. Based on this, a semi-supervised dynamic community algorithm SDCD based on non-negative matrix factorization, which effectively extracted the historical stability structure unit firstly, and then use it as a regularization item supervision of nonnegative matrix decomposition, to guide the network community detection on current moment. Experiments on the real network data sets show that the method has a higher community detection quality compared with existing methods, which can accurately mine the relationship among different time, and explore network evolution and the law of development more advantageously.

semi-supervised, dynamic, community detection, non-negative matrix factorization

TN915.0

A

10.11959/j.issn.1000-436x.2016039

2015-07-15；

2015-11-06

国家自然科学基金资助项目（No.61171108）；国家重点基础研究发展计划基金资助项目（No.2012CB315901, No. 2012CB315905）；国家科技支撑计划基金资助项目（No.2014BAH30B01）

The National Natural Science Foundation of China (No. 61171108), The State Key Development Program for Basic Research of China (No. 2012CB315901, No. 2012CB315905), The National Key Technology R&D Program (No.2014BAH30B01)

常振超（1987-），男，河北邯郸人，国家数字交换系统工程技术研究中心博士生，主要研究方向为社会网络结构分析。

陈鸿昶（1964-），男，河南郑州人，国家数字交换系统工程技术研究中心教授、博士生导师，主要研究方向为社会网络分析。

黄瑞阳（1986-），男，福建漳州人，博士，国家数字交换系统工程技术研究中心讲师，主要研究方向为社会网络分析。

于洪涛（1970-），男，河南郑州人，国家数字交换系统工程技术研究中心教授、硕士生导师，主要研究方向为社会网络分析。

刘阳（1986-），男，湖北随州人，国家数字交换系统工程技术研究中心博士生，主要研究方向为社会网络分析。