基于FPGA的磁悬浮轴承飞轮控制系统设计

刘鹏远，李建春，王晓瑜，肖跃华，曹扬

（北京航天控制仪器研究所，北京100039）



基于FPGA的磁悬浮轴承飞轮控制系统设计

刘鹏远，李建春，王晓瑜，肖跃华，曹扬

（北京航天控制仪器研究所，北京100039）

针对五自由度永磁偏置磁轴承飞轮，分析其结构参数及控制原理，设计了磁飞轮通用型电控系统。介绍了以FPGA为核心的控制系统构成，并阐述了控制器的设计策略，针对飞轮数据处理设计了一种通用型矩阵运算器。最终完成静态悬浮及低速旋转实验。

磁悬浮飞轮；FPGA；不完全微分PID；矩阵运算器

0　引言

磁悬浮轴承飞轮是空间卫星实现高精度姿态控制常用的执行机构。磁悬浮轴承技术是保障飞轮高效工作的关键，它利用电磁力将转子悬浮，使定、转子之间无机械接触，因此具有无磨损、无需润滑、使用寿命长、功耗低等优点。另外，磁悬浮轴承飞轮在高精度机床、飞轮储能电池、新能源汽车等方面都有越来越广泛的应用［1］。

磁轴承飞轮技术的关键在于磁轴承支撑技术，我国在磁轴承结构设计、控制策略等方面，都取得了长足的进展。

文献［2］提出一种针对飞轮控制的双滑膜变结构控制器，实验验证该控制器具有超调小、稳态误差小、响应速度快等优点；文献［3］提出章动失稳的主要原因是系统的相位滞后引起，进动失稳主要因为积分控制项对系统负阻尼作用引起，并给出了基于PID控制的解决方案；文献［4］实现了以DSP为核心的控制力矩陀螺控制器；文献［5］实现了给予FPGA的磁悬浮飞轮控制器的一体化设计；文献［6］介绍了磁悬浮系统神经网络建模与控制，并分析了磁悬浮轴承系统不确定性因素，采用开源软件实现了主动磁轴承的数字控制；文献［7］采用遗传算法实现了磁悬浮轴承控制系统的设计；文献［8］采用矩阵变换的方法实现飞轮电池能量转换及控制；文献［9］介绍了主动磁轴承抑制机械抖动的方法；文献［10］对主动磁轴承在多种控制模式下的鲁棒稳定性做了详细探讨；文献［11］利用自适应鲁棒控制，成功对柔性转子磁轴承抖动进行了抑制。

本文以现有永磁偏置磁轴承飞轮为研究对象，分析其结构参数及控制原理，分析了五自由度悬浮数学模型；设计了三电平PWM开关功率放大器和以FPGA为核心的控制器，实现了浮点PID算法。最终完成飞轮五自由度静态及低速旋转悬浮实验，并根据实验修正控制算法，最终获得较理想的控制效果。

1　系统模型

五自由度飞轮永磁偏置磁轴承控制系统结构如图1所示。系统由轴向磁轴承、径向磁轴承、电涡流位置传感器、信号调理电路、数字控制器、功率放大器组成。

飞轮系统中，每一组磁轴承以都差动方式提供回复力。轴向传感器单向工作，径向传感器差动工作。传感器实时监测飞轮的位置信号，并将其转化为电压信号。电压信号经调理电路处理和AD转换，作为反馈信号输入数字控制器，其中Z方向信号经过解算（4-3变换），由四个位置信息变成一个转子几何中心位置和绕X轴、Y轴转动的两个角度信息。反馈信号与系统给定比较，偏差作为五自由度控制器输入。输出中，Z方向位置与绕X轴、Y轴的角度信息再经3-4变换成为相应磁轴承的控制信号。控制信号经FPGA处理，产生24路PWM驱动信号，经开关功放，输出三电平PWM电压信号作用于磁轴承绕组线圈。线圈电流产生的磁场与永磁体磁场共同作用，产生回复力，使飞轮回到平衡位置，实现悬浮。磁悬浮轴承为位置-电流双闭环系统，采用电涡流传感器检测位置，霍尔传感器检测电流。

图1　五自由度磁悬浮飞轮系统结构Fig.1Structure of magnetic levitation flywheel system with five degrees of freedom

飞轮转速可达到3000r/min，在此条件下，转子被视为刚性转子，在工作范围内，轴承提供的电磁力与控制电流，转子位置有近似线性的关系：

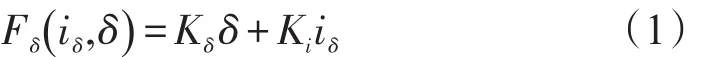
其中，Fδ为电磁力，Kδ为位置刚度，Ki为电流刚度，δ为转子位置，iδ为控制电流。

根据飞轮结构，当不计外力时，由牛顿第二定律可推导得系统五自由度运动微分方程为：

其中，m为转子质量，Jx、Jy、Jz为转子绕X轴、Y轴、Z轴的转动惯量，x、y、zO为转子在X、Y、Z方向的平动位移，θx、θy为转子绕X轴、Y轴的转动角度，Fx+、Fx-、Fy+、Fy-、Fz为磁轴承在X、Y、Z方向的平动回复力，MX、MY为磁轴承施加在X、Y方向的力矩，ωz为电机转速。由方程可知，转子平动自由度间不存在耦合，绕X轴、Y轴转动存在耦合。

对于径向平动自由度，以X轴为例，当不计外力时，轴向单自由度平动传递函数为：

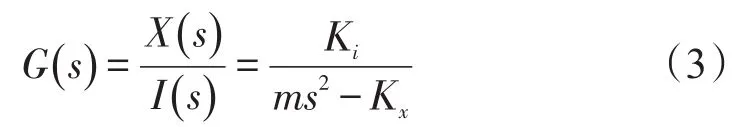
对系统采用闭环控制，以转子位置信号作为反馈量。轴向单自由度闭环系统框图如图2所示。

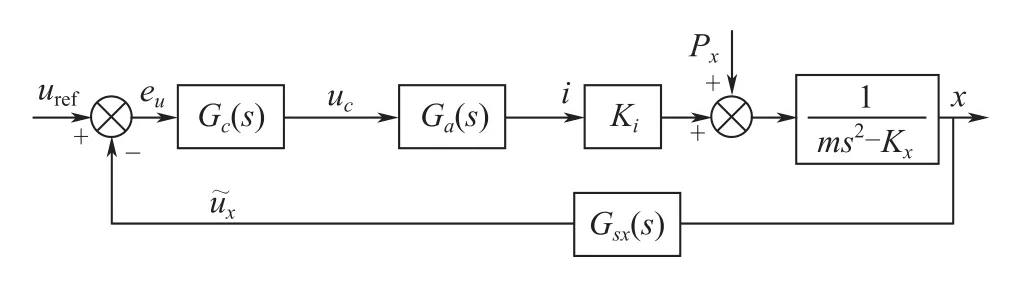
图2　单自由度闭环控制系统框图Fig.2Block diagram of closed-loop control system for single degree of freedom

则系统闭环传递函数为：

其中，Gc（s）为控制器传递函数，在传统控制方法中一般为PID控制器；Ga（s）为电流内环传递函数，正常工作时为常数Ka；Gsx（s）为位移传感器传递函数，正常工作时亦为常数，可设其为Ksx。

此时系统闭环传递函数为：

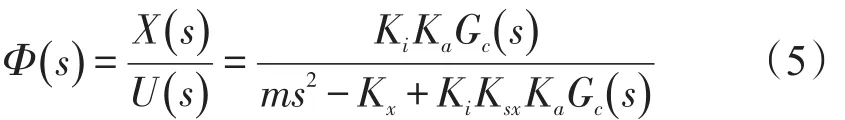
根据闭环系统的稳定劳斯判据，对于二阶系统，系统稳定的充分必要条件为闭环特征多项式系数都大于零，因此控制器必须至少含有微分环节及惯性环节，假设控制器为PD控制，

Gc（s）=Kcp+Kcds，则系统闭环传函为：

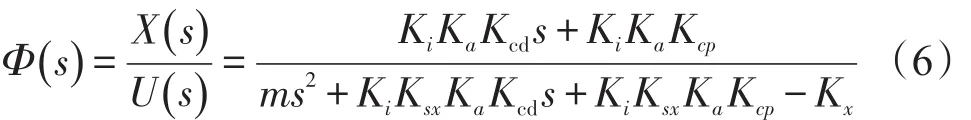
系统稳定需满足：KiKsxKaKcp-Kx＞0。

对于轴向运动（包括轴向平动、径向转动），控制系统框图如图3所示。

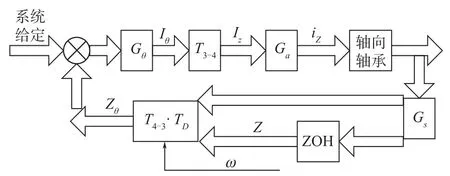
图3　轴向运动控制系统框图Fig.3Block diagram of axial motion control system

在轴向运动控制中，轴向传感器所测位置参数经4-3变换，转换为自由度，经控制器运算后再经3-4变换得出各轴承线圈中的控制电流。其中，Gθ为轴向运动解耦控制器，Iθ=［IZoIθxIθy］'为控制器输出，iz=［iz1iz2iz3iz4］'为线圈控制电流，Zθ=［zOθxθyżOθ̇xθ̇y］'为解算后轴向运动各自由度数据。Z=［z1（k）z2（k）z3（k）z4（k）z1（k-1）z2（k-1）z3（k-1）z4（k-1）］'为位置传感器采集数据。3-4变换矩阵，4-3变换及解耦矩阵，数据处理阵如下：

式中，t为采样频率。

2　控制器结构及算法实现

2.1控制系统整体结构

飞轮控制系统由以FPGA为核心的数字控制器、功放电路和传感器电路构成。鉴于磁悬浮轴承控制系统组成复杂，当某一路功放电路出现故障时，会使整个系统工作受到影响。因此将控制系统电路部分划分为控制板、功放板和信号采集板三部分，并做成可插拔式板卡。

FPGA程序主要包括AD采集、串口通信、数据处理、数字控制、PWM控制信号生成、顶层逻辑及时序分配等几个主要模块，如图4所示。在软件中，利用芯片内部双端口RAM作为数据传递媒介，将各功能模块相互隔离，使每个功能模块都可以独立工作。这种设计方式可以极大程度上减少数字电路中的竞争冒险和时序冲突，易于扩展和协同开发。

2.2AD采集与数据格式

本系统选用的AD转换芯片为AD7656，它是由ADI公司采用iCMOS工艺生产的，高集成度、6通道、16bit逐次逼近型ADC。其单通道采样率可达到250kbit/s，并且内置低噪声宽带宽采样保持放大器，能够处理输入频率达4.5MHz的信号。

图4　FPGA程序主要结构Fig.4Main structure of FPGA

利用二进制数直接计算有诸多不便，在加/减法操作后数据都要做溢出保护处理，在乘法操作后数据都需要做截短处理，这些处理都降低了计算精度，影响控制系统特性。因此，在数据处理和数字控制器中采用单精度浮点数。16位二进制定点数到单精度浮点数的转换利用ALTERA提供的IP核ALTFP_CONVERT来实现。

2.3数据处理

数据处理主要包括3-4变换、4-3变换及解耦、滤波等。数据处理的核心在于利用实现矩阵算法。浮点乘加运算需要消耗大量逻辑资源，利用ALTERA浮点乘法与加法IP核，集合流水线，实现了一种矩阵运算器，可以很方便地实现矩阵与矩阵乘、矩阵与列向量乘、矩阵与常数乘等运算。可以利用最少的逻辑资源和较少的时钟周期实现极大的运算量。

实现浮点乘法器需要5个时钟周期，加法需要8个时钟周期。以矩阵与列向量乘为例，运算器结构如图5所示，乘法器的输出直接作为加法器的一个输入，加法器的输出作为自身的另一个输入。系数矩阵保存在一个8×8RAM中，传感器AD采集数据保存在1×8RAM中。运算开始前，运算器中所有寄存器清零，运算开始后每个时钟周期从系数矩阵读出一组乘数（mdata1），每8个周期从数据矩阵中读出一组乘数（mdata2），5个周期后，乘法器开始输出有效结果，13个周期后，加法器开始输出有效结果，该结果与乘法器输出作和，69个周期后，即可完成矩阵与列向量乘运算，并把结果保存在另一个1×8RAM中。

图5　矩阵运算器示意图Fig.5Diagrammatic sketch for matrix computation

2.4数字控制器设计

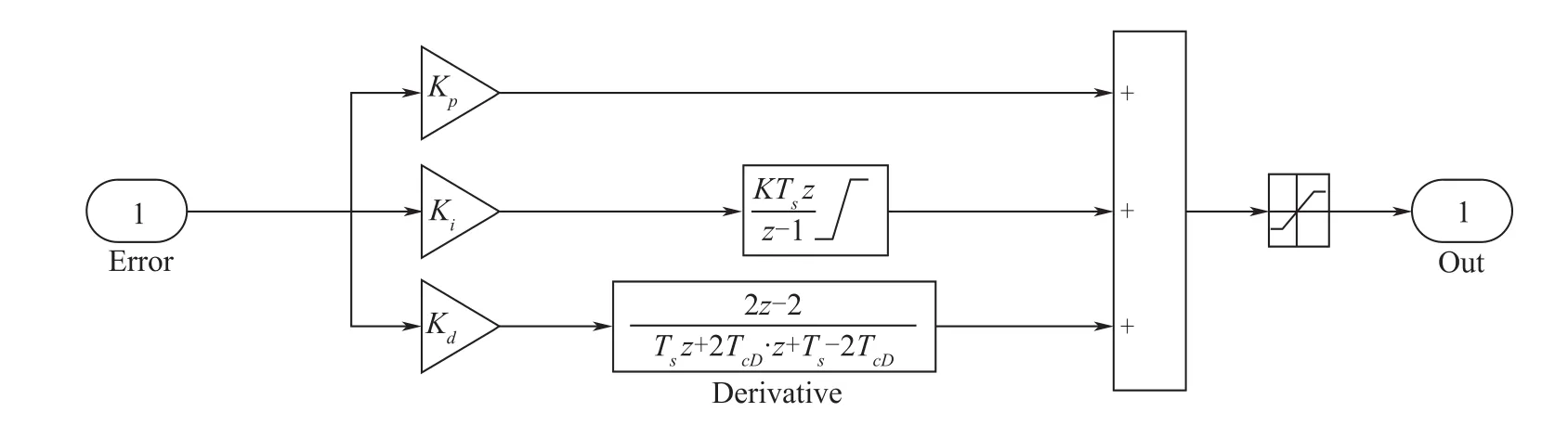
图6　数字式PID控制器结构Fig.6Structure for digitized PID controller

PID控制器脉冲响应传递函数为：

离散化后的比例通道输出：

积分通道输出：

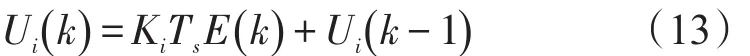
微分通道输出：

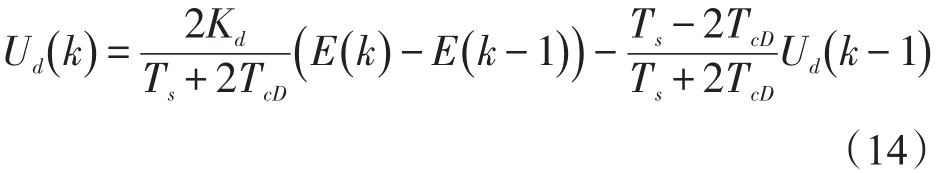
控制器输出为：

PID算法实现过程如图7所示，运算中每一个步骤都占用8个时钟周期。

图7　PID控制算法流程Fig.7Flow path for PID algorithm

3　实验

将程序下载至FPGA完成起浮实验。图8中，X、Y、Z1、Z2、Z3、Z4分别为各轴承对应位置传感器输出波形。电路中，径向位置传感器放大倍数为10mV/μm，轴向传感器放大倍数为7mV/μm。

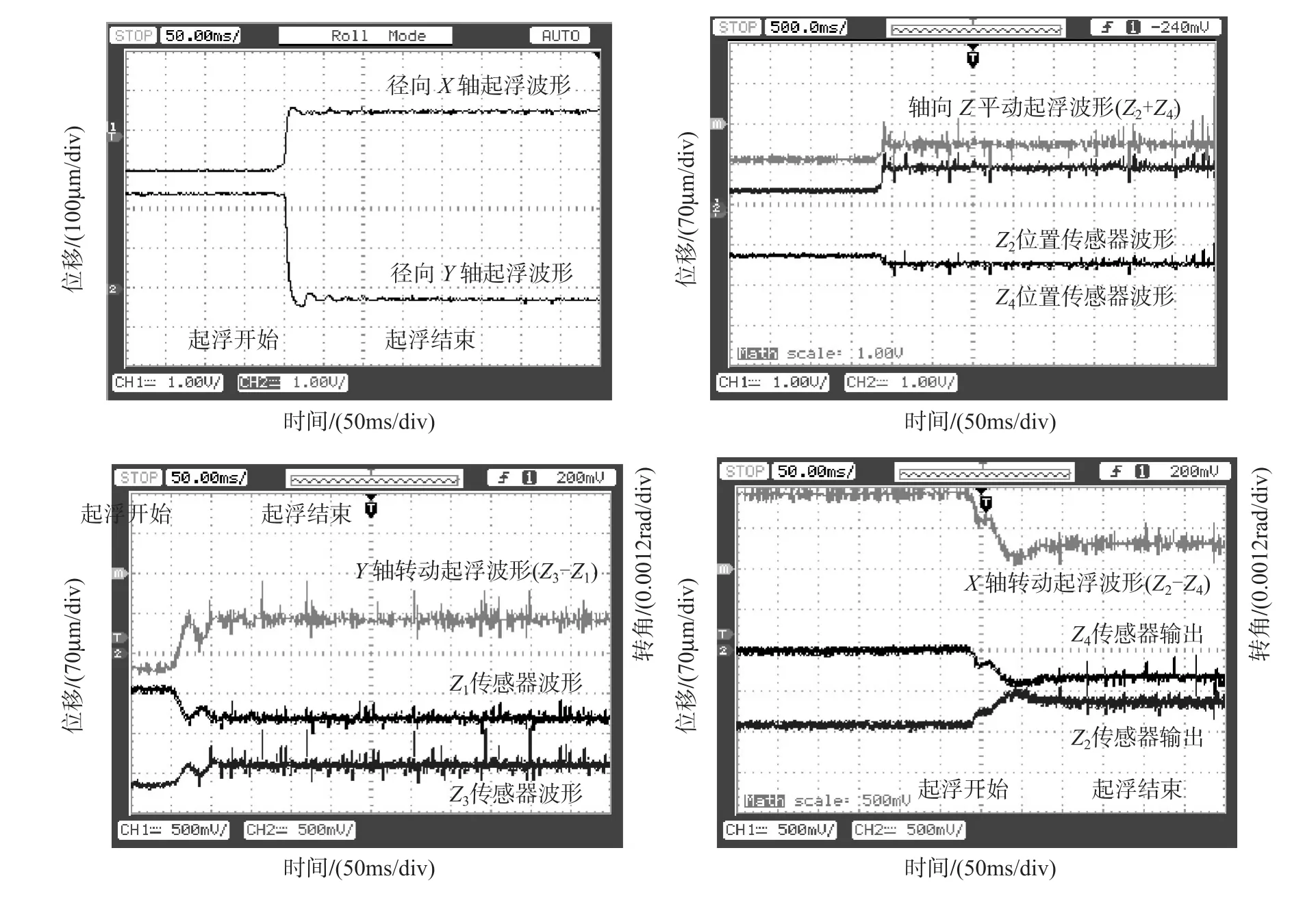
图8　飞轮静态悬浮传感器波形Fig.8Wave form of flywheel static levitation

当飞轮未悬浮时，轴心轨迹如图9所示，飞轮转子转动受保护轴承支撑。转子轴心轨迹在未悬浮时并不是圆形。其主要原因是飞轮转子轴向中心线与定子中心线间存在偏角。该偏角在X轴、Y轴转动起浮后可以减小到较理想状态。

飞轮稳定悬浮后，令其低速（2000r/min）旋转，其轴心轨迹如图10所示。由图10可知，转子轴心在低速旋转时X方向波动范围为［-60，70］μm，Y方向波动范围为［-90，30］μm，转子波动范围约为可移动气隙的30%。

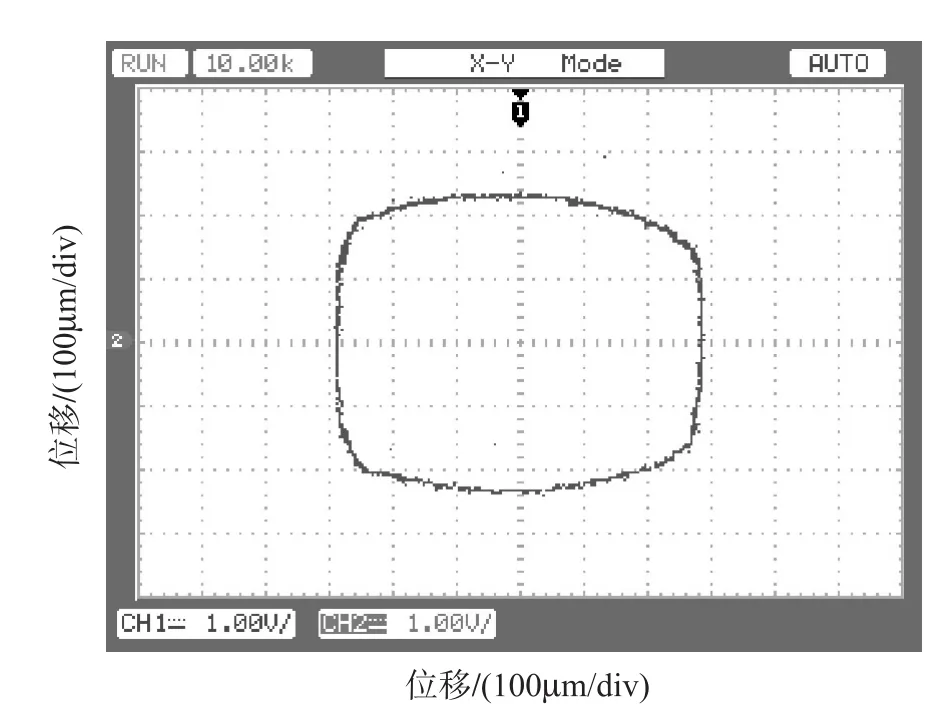
图9　未悬浮轴心轨迹Fig.9Locus for axle centre when the flywheel is not suspended

图10　稳定悬浮后轴心轨迹Fig.10Locus for axle centre when the flywheel is suspended

4　结论

本文介绍了磁轴承飞轮的控制系统模型，并以此为基础，实现了以FPGA为核心的数字控制系统，通过实验，证明该控制器可以实现飞轮的稳定悬浮。

［1］夏刚，李建春，陈效真，马磊忠.磁悬浮空间惯性执行机构浅说［C］.磁悬浮空间惯性执行机构资料汇编：1-12. XIA Gang，LI Jian-chun，CHEN Xiao-zhen，MA Leizhong.Elementary introduction for magnetic space of inertial actuator［C］.Compilation of magnetic space of inertial actuator：1-12.

［2］周新秀，房建成，刘刚.磁悬浮反作用飞轮电机滑模变结构控制［J］.电机与控制学报，2008（5）：487-492. ZHOU Xin-xiu，FANG Jian-cheng，LIU Gang.Reaction flywheel motor sliding mode variable structure control system［J］.Electric Machines and Control，2008（5）：487-492.

［3］董淑成，房建成，俞文伯.基于PID控制的主动磁轴承-飞轮转子系统运动稳定性研究［J］.宇航学报，2005（3）：296-300+306. DONG Shu-cheng，FANG Jian-cheng，YU Wen-bo.Active magnetic bearing flywheel based on PID controllerstudy on the motion stability of flywheel rotor system［J］. Journal ofAstronavigation，2005（3）：296-300+306.

［4］李巍，房建成，俞文伯，赵建辉.控制力矩陀螺用主动电磁轴承数字控制系统设计与实现［J］.中国惯性技术学报，2005（4）：47-51. LI Wei，FANG Jian-cheng，YU Wen-bo，ZHAO Jianhui.Design and realization of a digital control system for active magnetic bearing of control moment gyroscope［J］.Journal of Chinese Inertial Techonology，2005 （4）：47-51.

［5］张立，刘昆.基于FPGA的飞轮磁轴承一体化控制系统设计［J］.电机与控制学报，2012（4）：84-90. ZHANG Li，LIU Kun.Integrated control system design of magnetic bearings for flywheel based on FPGA［J］. Electric Machines and Control，2012（4）：84-90.

［6］Harland E Alpaugh，Jr.Digital control of an experimental active magnetic bearing rotor using open source software ［D］.Tufts University School of Engineering，2007.

［7］Yong Teng.Magnetic bearing system design using a genetic algorithm［D］.The Faculty of Engineering and Applied Science，University of Virginia，1999.

［8］Bingsen Wang.Flywheel based AC power conditioning system using a matrix converter［D］.University of Wisconsin-Madison，2006.

［9］Min Chen.Machining chatter control using active magnetic bearings［D］.The Faculty of Engineering and Applied Science，University of Virginia，2007.

［10］Guoxin Li.Robust stabilization of rotor-active magnetic bearing system［D］.The Faculty of Engineering and Ap-plied Science，University of Virginia，2007.

［11］Hans A.DeSmidt.Robust-adaptive active vibration control of alloy and flexible matrix composite rotorcraft drivelines via magnetic bearings：theory and experiment［D］.The Pennsylvania State University，2005.

［12］Todd Andrew Begalke.Synchronous reluctance drive for flywheel batteries［D］.University of Minnesota，2006.

Design of Control System for Magnetically Suspended Flywheel Based on FPGA

LIU Peng-yuan，LI Jian-chun，WANG Xiao-yu，XIAO Yue-hua，CAO Yang
（Beijing Institute ofAerospace Control Devices，Beijing 100039）

According to the five degree of freedom of permanent manget biased magnetic bearing flywheel，we analyzed the structure and control principle of it.A general electric control system of magnetic flywheel was designed.In this paper a composition of control system with FPGA as the core was introduced.And the design strategies of the controller was expounded.In the view of the data processing for flywheel，a general matrix computation was designed.Finally the static levitation and low-speed rotation experiment were completed.

magnetically suspended flywheel；FPGA；incomplete differential PID controller；matrix computation

TH133.7文献标识志码：A

1674-5558（2016）03-01043

10.3969/j.issn.1674-5558.2016.01.015

刘鹏远，男，硕士，工程师，研究方向为磁悬浮轴承控制、电动舵机控制等。

2014-12-09