利用分解校正矩阵确定搜索方向的BFGS算法

柳力

（吉林市广播电视大学教学处，吉林吉林132002）

利用分解校正矩阵确定搜索方向的BFGS算法

柳力

（吉林市广播电视大学教学处，吉林吉林132002）

本文把正定矩阵关于向量的等内积分解算法应用于改进BFGS算法中搜索方向的计算.通过建立不依赖于搜索方式的用分解矩阵表达的校正公式，给出了用Hesse近似矩阵的等内积分解矩阵确定搜索方向的BFGS算法.

BFGS算法；校正矩阵；等内积分解；搜索方向；算法

1　引言

利用正定矩阵关于向量的等内积分解算法［1］，文［2］提出了由校正矩阵的等内积分解矩阵确定搜索方向的拟Newton算法．即对于无约束最优化问题

其中f：Rn→R1是连续可微函数，通过建立Hesse近似矩阵B关于目标函数梯度向量的等内积分解矩阵的校正公式，计算搜索方向的一种新算法．

以拟Newton算法中最有代表性的BFGS算法为例，当记xk为迭代点，sk=xk+1-xk，yk=gk+1-gk，gk=▽f（xk），则对B和对H的BFGS校正公式分别为

在求迭代点xk+1处的搜索方向dk+1时，一般是解方程组

而不是用（1.3）式直接计算.

采用（1.4）式的计算量显然大于用（1.5）式，“舍近求远”的原因是，由于计算误差的存在，实际计算时用（1.3）式可能出现Hk+1不正定甚至奇异的情况．而（1.2）式可以化为据此，Gill与Murray提出了利用Cholesky分解技术解方程组（1.4）的方法.即先对Bk+1作 Cholesky分解：，其中Lk+1为单位下三角阵，Dk+1为对角阵，再依次解方程组

同时利用（1.6）式，给出由Lk，Dk求Lk+1，Dk+1的迭代公式，使实际计算时不必每次迭代都进行一次Bk的Cholesky分解，具体算法详见文［3-5］.

而文［2］提出的改进算法，则是运用了正定矩阵关于向量的等内积分解算法，通过求Bk+1关于gk+1=▽f（xk+1）的等内积分解矩阵.即满足条件

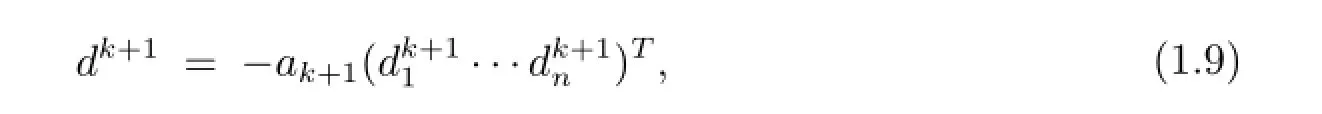
显然文［2］给出了求搜索方向的另一种路径，但文［2］中的相关结论，都是在精确线搜索条件下给出的，所以理论意义大于实际应用．在拟Newton算法中BFGS算法是最有代表性的一个算法，带Wofle搜索的BFGS算法具有全局收敛和超线性收敛性（参见文［4］），与拟Newton算法中的其它算法比较其收敛速度和数值稳定性都是最好的．本文就以BFGS算法为研究对象，通过建立不依赖搜索方式的用分解矩阵表达的校正公式，给出用Hesse近似矩阵的等内积分解矩阵确定搜索方向BFGS新算法.

2　用分解矩阵形式表达的BFGS校正公式

当记uk=yk，vk=gk+1，wk=gk.由文［2］定理2.2，在精确线搜索条件下对于BFGS校正公式（1.2）.若已求得Bk关于gk的等内积分解矩阵，则Bk+1关于gk+1的等内积分解矩阵

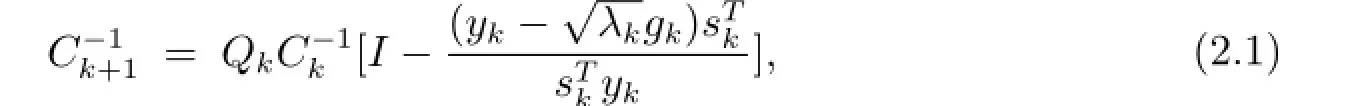
其中λk=，Qk=，σk=wk+tkvk，.由文［2］定理2.3，初始校正矩阵B0=I关于g0的等内积分解矩阵

其中σ0=

引理2.1设u，v†Rn，若β/=0，γ/=0，vTu=β-1+γ-1，则矩阵I-βuvT非奇异，并且

引理2.2对于BFGS校正公式（1.2），若Bk关于gk的等内积分解矩阵为.记

则Bk+1=，并且

证注意到sk=xk+1-xk=αkdk，其中αk为步长，于是Bksk=-αkgk.直接计算得

所以Bk+1=.由于

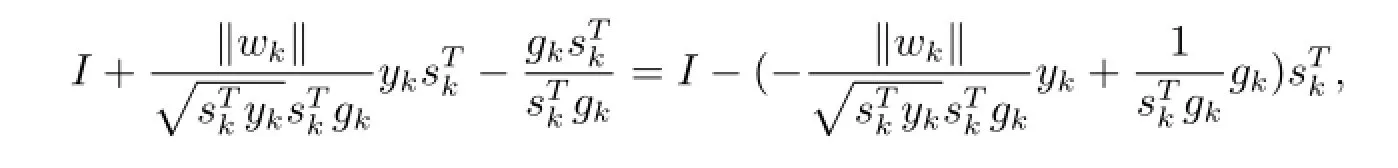
由引理2.1，易得

引理2.3若0/=δk†Rn，记Qk=，其中σk=δk+，则

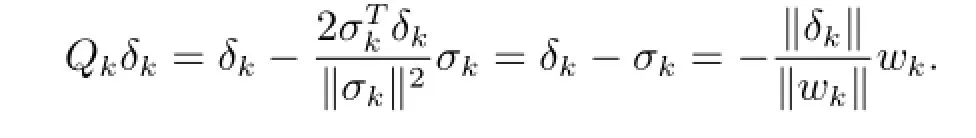
证毕.

当记

定理2.1对于BFGS校正公式（1.2），若已求得Bk关于gk的等内积分解矩阵，则Bk+1关于gk+1的等内积分解矩阵

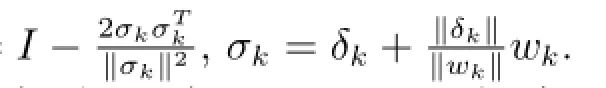
证注意到Qk为Householder矩阵，=I，所以

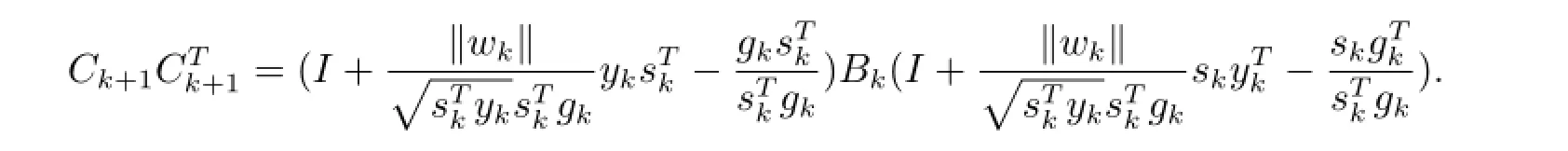
故由引理2.2知Bk+1=.再由引理2.3得

其中ak+1=.故由（2.7）式定义的为Bk+1关于gk+1的等内积分解矩阵.

推论2.1在精确线搜索条件下，（2.7）式与（2.1）式等价，即（2.1）式为（2.7）式的特例.

3　利用分解校正矩阵确定搜索方向的BFGS算法

显然，把由（2.2）式和（2.7）式为分解校正矩阵，由（1.9）式计算搜索方向的步骤替换到BFGS算法中对应的步骤里，就可以构成利用分解校正矩阵确定搜索方向的BFGS新算法.由于分解校正矩阵的迭代运算仅是非奇异矩阵到非奇异矩阵的迭代运算，因此计算精度的要求应低于原BFGS算法中对称正定矩阵到对称正定矩阵的迭代运算.

新的BFGS算法：

步1取初始点x0，ε≥0，计算g0=g（x0）.若‖g0‖≤ε，则停止运算；否则转步2.

步2令k=0；对初始矩阵B0=I作关于g0的等内积分解，求出分解矩阵和

步3求搜索方向dk：dk=.其中，（j=1，2，···，n）是的第j列元素之和.

步4一维搜索：由线性搜索求出步长因子αk.

步5令xk+1=xk+αkdk，计算gk+1=g（xk+1），若‖gk+1‖≤ε，则停止计算；否则转步6.

步6由公式（2.7）求出Bk+1关于gk+1的等内积分解矩阵和系数ak+1=ak.

步7令k=k+1，转步3.

［1］柳力.一个矩阵分解算法的推广及应用［J］.数学的实践与认识，2011，41（21）：239-243.

［2］柳力.由校正矩阵的等内积分解矩阵确定搜索方向的拟牛顿算法［J］.数学的实践与认识，2013，43（10）：214-219.

［3］Gill P E，Murray W.Quasi-Newton methods for unconstrained optimization［J］.Insti.Math.Appl.，1972，（9）：91-108.

［4］席少霖.非线性最优化方法［M］.北京：高等教育出版社，1992.

［5］邓乃扬等.无约束最优化计算方法［M］.北京：科学出版社，1982.

BFGS ALGORITHM BY USING THE DECOMPOSITION MATRIX OF THE CORRECTION MATRIX TO OBTAIN THE SEARCH DIRECTION

LIU Li
（Department of Teaching，TV University of Jilin City，Jilin 132002，China）

In this paper，the equal inner product decomposition algorithm of positive definite matrix is applied to improve the search direction calculation in BFGS algorithm.By setting up the correction matrixes of both independent search mode and decomposition matrixes expression，BFGS algorithm is put forward，in which search directions are obtained by using equal inner product decomposition matrixes of the Hesse approximate matrixes.

BFGS algorithm；correction metrix；equal inner product decomposition；search direction；algorithm

MR（2010）主题分类号：90C30O221.2

A

0255-7797（2016）05-1035-05

2014-02-22接收日期：2014-07-31

吉林省教育厅“十二五”科学技术研究项目资助（2014598）.

柳力（1958-），男，吉林吉林，副教授，主要研究方向：数学规划.

2010 MR Subject Classification：90C30