PERIODIC SOLUTIONS OF DAMPED IMPULSIVE SYSTEMS
2016-10-13JIANGLixinDINGWei
JIANG Li-xin,DING Wei
(1.Department of Mathematics and Physics,Nantong Normal College,Nantong 226006,China)
(2.School of Sciences,Nantong University,Nantong 226007,China)
PERIODIC SOLUTIONS OF DAMPED IMPULSIVE SYSTEMS
JIANG Li-xin1,DING Wei2
(1.Department of Mathematics and Physics,Nantong Normal College,Nantong 226006,China)
(2.School of Sciences,Nantong University,Nantong 226007,China)
In this paper,we study the existence of periodic solutions of damped impulsive problems via variational method.By presenting a new approach,we obtain the critical points of impulsive systems with periodic boundary under some assumptions,which generalizes the known results and enriches the research methods of impulsive problems.
critical points;impulses;periodic boundary;constraint
2010 MR Subject Classification:45M15;65L10
Document code:AArticle ID:0255-7797(2016)05-0920-09
1 Introduction
Impulsive differential equations arising from the real world describe the dynamic of processes in which sudden discontinuous jumps occur.In recent years,impulsive problems attracted the attention of a lot of researchers and in consequence the number of papers related to this topic is huge,see[1-6]and their references.For a second order differential equation x'+f(t,x,x')=0,one usually considers impulses in the position x and the velocity x'. However,in the motion of spacecraft one has to consider instantaneous impulses dependent only on the position,and the result in jump is discontinuous in velocity,but with no change in position[7,8].Let t0=0<t1<t2<···<tp<tp+1=2π.Recently,the following Dirichlet boundary value problems with impulses

were studied by variational method in[9,10],where f:[0,2π]×R→R is continuous,g∈C[0,2π],and the impulse functions Ij:R→R is continuous for every j.After that,impulsive problems(1.1)-(1.2)with periodic boundary
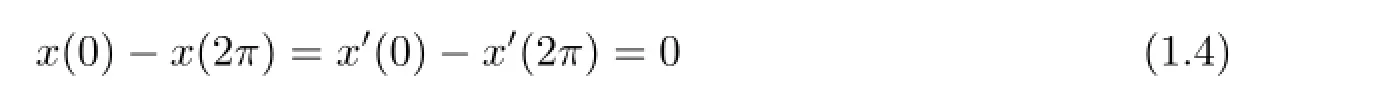
was also investigated in[6]when g(t)≡0.
Generally,people are used to obtain the critical points of impulsive problems via Mountain pass theorem or Saddle point theorem.In this paper,we use Lagrange multipliers theorem,that is conditional extremum theory,to investigate impulsive problems(1.1)-(1.2)with periodic boundary

The organization of the paper is as follows.In Section 2,we give variational structure of impulsive problem(1.1)-(1.2)-(1.5).In Section 3,critical points corresponding to periodic solutions of impulsive problems(1.1)-(1.2)are obtained by constrain theory.
2 Variational Structure
In this section,we always assume that f:R×R→R is 2π-periodic in t for all x∈R and satisfies the following carath´eodory assumptions:
(1)for every x∈R,f(·,x)is measurable on[0,2π];
(2)for a.e.t∈[0,2π],f(t,·)is continuous on R;

Multiplying equation(1.1)by eG(t),we can see that impulsive problem(1.1)+(1.2)+(1.5)is equivalent to

We now investigate impulsive system(2.1)+(1.2)+(1.5).Define Hilbert space

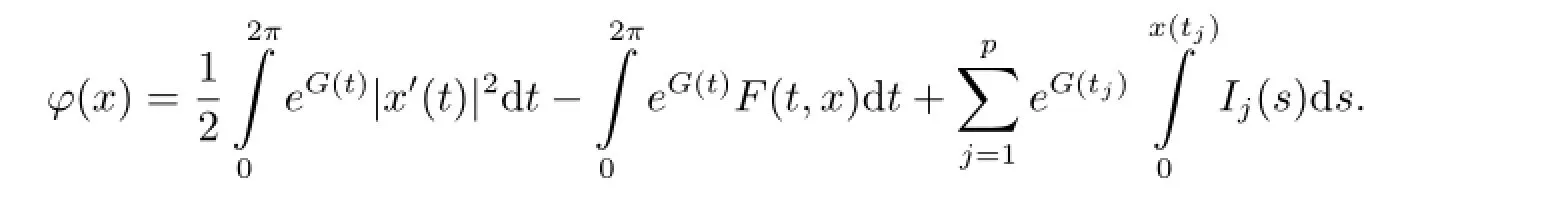
Proposition 2.1 Under our assumptions,functional φ(x)is weakly lower semi-continuous on


The following result is evident.


Proposition 2.3 Under our assumptions,if x∈is a critical point of φ,then x is one 2π-periodic solution of problem(2.1)+(1.2)+(1.5).
Proof Let x be a critical point of φ in,then for every v∈we have

We now check that x satisfies(2.1)+(1.2)+(1.5).
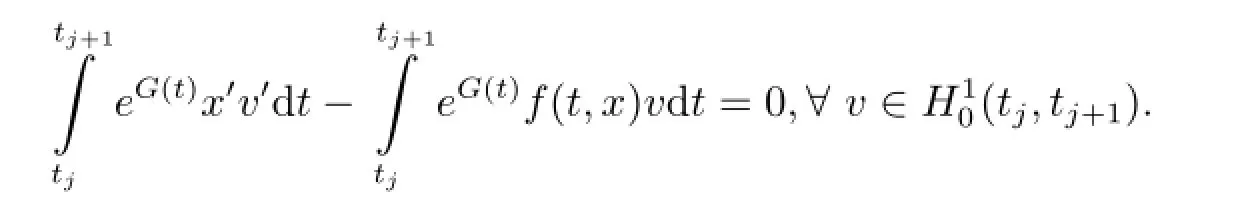
It implies that(eG(t)x')'+eG(t)f(t,x)=0 a.e.t∈[tj,tj+1].Hence x satisfies

That is,x satisfies equation(2.1).
0.By integration by parts,we have

Combining with(2.2),which implies that

Hence

This is just condition(1.2).
On the other hand,in(2.2),let v=1,then

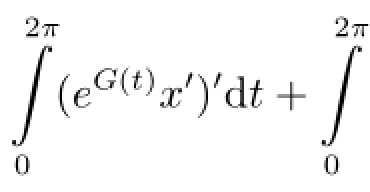


Thus we complete the proof.

3 Critical Points in Constraints
The following Lagrange multipliers theorem is well known(see Theorem 2.1 in[11]or Theorem 3.1.31 in[12]).
Lemma 3.1 Let φ∈C1,R)and M={x∈:ψj(x)=0,j=1,···,n},where ψj∈C1,j=1,···,n,andare linearly independent foreach x∈Then if u∈M is a critical point of φ|M,there exist λj∈R j=1,···,n, such that

We now give the following minimization principle in constraint M.
Lemma 3.2(see Theorem 1.1 in[11])Let M be a weakly closed subset of a Hilbert space X.Suppose a functional φ:M→R is
(i)weakly lower semi-continuous,
(ii)φ(u)→+∞as‖u‖→∞,u∈M, then φ is bounded from below and there exists u0∈M such that φ(u0)=
Using the above lemmas,the author of[11]consider the following Neumann problem

for some suitable Ω⊂RNand f(u)under natural constraints(see[11]).Inspired by his work,in this section,we take our attention to find the critical points of functional φ over a set of constraints M⊆

and

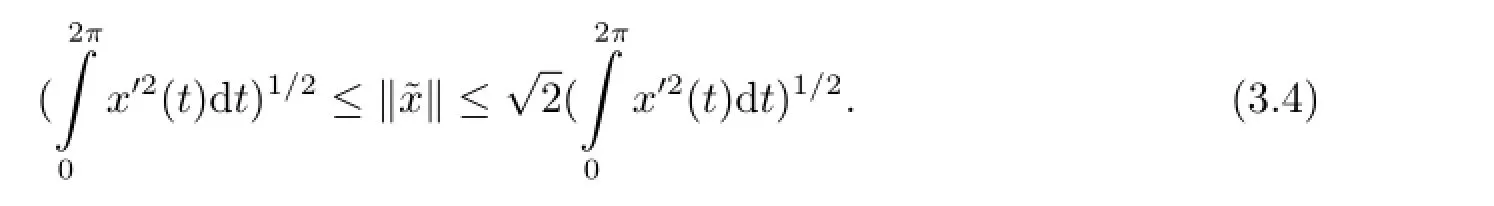
Besides those conditions given to f(t,x),g(t)and Ij(x),j=1,···,k in Section 2,we also assume that there exist constants α,β>0,ξj∈R,j=1,···,k,such that
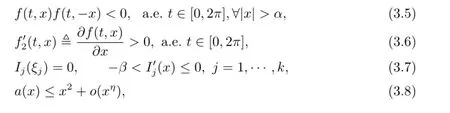
It is easy to see that
where constant 0≤η<2 and the function a is from carath´eodory assumption(3).
For convenience,we denote A=max{eG(t)}and B=min{eG(t)},then A,B>0.
Theorem 3.3If above assumptions hold and 6B-A(2‖b‖1+pβ)π>0,then problem (1.1)-(1.2)-(1.5)has at least one solution.
Remark 3.4We only need to prove that problem(2.1)-(1.2)-(1.5)has at least one solution.


Then by conditions(3.6)and(3.7),one has Γ'(x)/=0,which indicates that Γ'(x)linearly independent for each x∈
Remark 3.5It is easy to see that,by conditions(3.5)-(3.7),we have that,∀u∈there exists a unique c∈R such that u+c∈M.In fact,∀u∈one has that u is continuous and the functioneG(tj)Ij(u(tj)+c)defined on R is continuous and strictly increasing,moreover
Lemma 3.6Under our assumptions,is a critical point of φ if and only if x∈M and x is a critical point of φ|M.
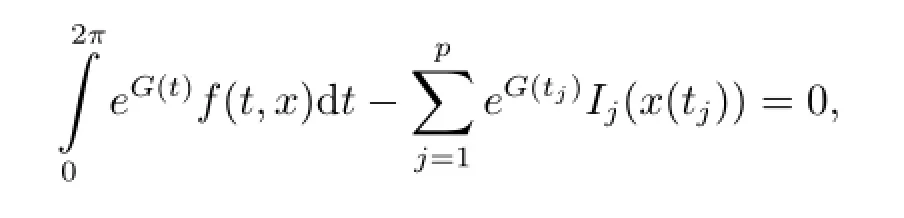
i.e.,x∈M,and hence x is a critical point of φ|M.
On the other hand,if x is a critical point of φ|M,by Lemma 3.1,there exists λ∈Rsuch that for every

Choosing v=1 and observing that x∈M,we have

which follows that λ=0 since>0 and≤0.Putting it into(3.9),one has φ'(x)=0.
Thus we complete the proof.
To functional

we have the following results.
Lemma 3.7Under our assumptions,we have
(i)Φ(u+c)≤Φ(u),∀u+c∈M,where u∈,c∈R.
(ii)Let un+cn∈M,where un∈and cn∈R.Then if‖un+cn‖→∞,one has‖un‖→∞.

The above two inequalities give that

which follows(i).
Next,we turn to prove(ii).Define functional Ψ:×R→R by the following

Because of the strict increase of Ψ(u,·),when n is big enough,we have
0=Ψ(v,c(v))<Ψ(v,cn)=Ψ(v,cn)-Ψ(vn,cn)

as n→∞.It is contradictory.
Thus we complete the proof.
Proof of Theorem 3.3Without loss of generality,we may assume that a(x)≤x2in condition(3.8)and ξj=0,j=1,2,···,p in condition(3.7).Then under our assumptions,one has

It implies that
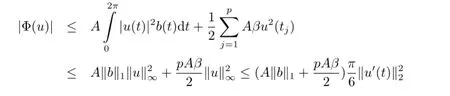

Since 6B-A(2‖b‖1+pβ)π>0,by(3.4)and(ii)of Lemma 3.7,we have φ(u+c)→+∞as ‖u+c‖→∞,u+c∈M.
On the other hand,M is weakly closed and φ is weakly lower semi-continuous,therefore by Lemma 3.2,there exists at least one critical point x∈M of φ|M.Then by Lemma 3.6,we complete the proof.
References
[1]Nieto J J.Basic theory for nonresonance impulsive periodic problems of first order[J].J.Math. Anal.Appl.,1997,205(2):423-433.
[2]Dong Y.Sublinear impulse effects and solvability of boundary value problems for differential equations with impulses[J].J.Math.Anal.Appl.,2001,264(1):32-48.
[3]He Z,Yu J.Periodic boundary value problems for first-order impulsive ordinary differential equations[J].J.Math.Anal.Appl.,2002,279(1):1223-1232.
[4]Nieto J J,O'Regan D.Variational approach to impulsive differential equations[J].Nonl.Anal. (RWA),2009,10(2):680-690.
[5]Zhang X Z,Liu B.Existence of positive periodic solutions to a nonautonomous delay differential equation with impulses[J].J.Math.,2007,27(2),157-164.
[6]Ding W,Qian D.Periodic solutions for sublinear systems via variational approach[J].Nonl.Anal. (RWA),2010,11(4):2603-2609.
[7]Carter T E.Optimal impulsive space trajectories based on linear equations[J].J.Optim.The.Appl.,1991,70(2):277-297.
[8]Carter T E.Necessary and sufficient conditions for optimal impulsive rendezvous with linear equations of motion[J].Dynam.Contr.,2000,10(3):219-227.
[9]Nieto J J.Variational formulation of a damped Dirichlet impulsive problem[J].Appl.Math.Lett.,2010,23(8):940-942.
[10]Xiao J,Nieto J J.Variational approach to some damped Dirichlet nonlinear impulsive differential equations[J].J.Franklin Inst.,2011,348(2):369-377.
[11]David G C.An invitation to variational methods in differential equations[M].Boston,Basel,Berlin:Birkh¨auser,2007.
[12]Berger M S.Nonlinearity and functional analysis[M].San Diego,US:Els.Sci.Publish.Co.Inc.,1977.
[13]Mawhin J,Wilem M.Critical point theory and Hamiltonian systems[M].Berlin,Heidelberg,New York:Springer-Verlag,1989.
带阻尼项的脉冲系统的周期解
姜黎鑫1,丁卫2
(1.南通师范高等专科学校数理系,江苏南通226006)
(2.南通大学理学院,江苏南通226007)
本文利用变分法研究了带阻尼项的脉冲系统的周期解.采用一种新的方法,在一些条件下证明了带周期边界条件的脉冲系统存在临界点.本文不仅推广了已有的结果而且还丰富了研究脉冲系统的方法.
临界点;脉冲;周期边界;限制
MR(2010)主题分类号:45M15;65L10O175.13;O176.3
date:2016-03-15Accepted date:2016-04-22
Supported by National Natural Science Foundation of China(11501308).
Biography:Jiang Lixin(1982-),female,born at Qidong,Jiangsu,master,major in ordinary differential equation.
猜你喜欢
杂志排行
数学杂志的其它文章
- SOME RESULTS FOR TWO KINDS OF FRACTIONAL EQUATIONS WITH BOUNDARY VALUE PROBLEMS
- ROBUST STABILIZATION OF UNCERTAIN STOCHASTIC SYSTEMS WITH TIME-VARYING DELAY AND NONLINEARITY
- EQUIVALENCE BETWEEN TIME AND NORM OPTIMAL CONTROL PROBLEMS OF THE HEAT EQUATION WITH POINTWISE CONTROL CONSTRAINTS
- ESSENTIAL NORMS OF THE GENERALIZED VOLTERRA COMPOSITION OPERATORS
- THE MINIMAL SOLUTION OF A SPECIAL ANTICIPATED BACKWARD STOCHASTIC DIFFERENTIAL EQUATION
- THE APPLICATION OF THE BASIN OF ATTRACTION TO THE EXISTENCE AND UNIQUENESS OF SOLUTIONS FOR THE SECOND ORDER PARABOLIC BOUNDARY VALUE PROBLEM
