城市发展规模理论：国外前沿研究回顾

汤　勇



城市发展规模理论：国外前沿研究回顾

汤勇

（湖南城市学院城市管理学院，湖南益阳413000）

Zipf定律的统计学意义及对城市发展规模的借鉴意义、城市合理规模及Zipf定律适用范围是国外城市发展规模理论的三类前沿问题。从创新驱动的角度总结国外城市发展规模研究的进展并讨论创新的过程性特征与城市发展的契合要求，认为城市是一种初期“原型产品”生产和后期“规模产品”生产的均衡体；从人力资本积累角度进行文献回顾，其结论是区域外部性和人力资本的外部性是驱动城市规模发展的主要原因。上述三类理论中，Zipf具备统计实证意义，而创新驱动与人力资本积累理论具备解释性意义。

城市规模；Zipf定律；创新过程；外部性

一、前言

2012年，国务院印发《关于调整城市规模划分标准的通知》，以常住城市人口为标准，将中国661个城市划分为五类七档。由于城市分类标准以现有人口数量为基础，缺少对城市人口集聚形成内在机理的探讨，对于直接指导城市发展、实现功能定位缺少理论依据。在新型城镇化全面推进过程中，一批以城市群为主体形态的城市群出现，使得部分城市边界模糊，造成部分区域在城市规模设定与控制上面临依据不足，严重影响了城市发展战略的制定，直接导致城市福利制度改革、户口及计划生育政策等的实施困难。针对城市规模问题，国内既有研究较多地遵循古典主义经济学思路，强调城市系统完善、区域中心地位及自然优势等城市形成与演化因素驱动，在研究范式上呈现出以现象解释现象的特征，造成理论框架单一和不完整，整体缺少预测与诊断能力。

本文针对以上缺陷，从文献回顾角度重点介绍三类城市发展规模理论，以期为学者们深入探讨我国城市规模合理性提供依据。一类是基于随机增长过程，主要基于Zipf定律，强调从统计学角度分析单个城市与城市整体分布规律；第二类强调其经济特征，以Duranton研究为基础，试图从创新驱动角度发掘城市规模的形成与城市内部均衡。第三类从人力资本积累的微观发展角度阐述城市的形成与演化机理，进而确定城市规模。

二、Zipf定律对城市规模分布的解释

Zipf定律由G. K. Zipf提出，表述为“自然语言语料库里，一个单词出现的次数与它在频率表里的排名成反比”，该规律被普遍运用于具备大样本的统计中。[1]一些学者受此启示，开始探讨城市规模排名（位序）与其人口数量（规模）的问题。在统计环节上，具体操作如下：将一个国家的城市按由大到小排列，然后计算位序－规模关系：

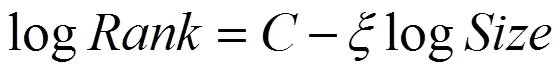
下面从统计角度来分析Zipf定律解释城市规模分布的合理性：

一是从乘数过程解释Zipf定律统计规律。借鉴Gabaix& Ioannides（2004）研究，视某一经济体（经常以一个国家为代表）具有固定人口规模，且这个经济体中含有若干数量城市。在期和期，城市按照的规律增长。采用Gibrat定律，假定不同城市按照相同的期望增长水平及方差增长，即均服从分布函数独立同分布。在期以后，城市规模为：

二是从加数过程解释Zipf定律。加数过程最早由Simon提出，[7]从本质上说，Simon模型假设总人口随时间按照既定增量方式增长，即城市人口规模增加与城市已有人口数量呈比例的规律出现。结合优先连接规律，认为某一个城市吸引新增人口的概率与该城市本身人口数量相关，也就是说某一外来人口进入该城市的概率等于该城市人口与所在经济体总人口比。在概率选择下，能保证各城市人口分布幂率性，即城市规模分布服从Zipf定律。

三是将乘数过程与加数过程相结合反映城市随机增长。本文结合Eeckhout[8]模型进行统计解释。假设存在一个经济体内的连续性城市集，城市在时期提供生产力水平，并认为该城市只具备唯一生产要素。设为城市在时期的人口数量，集聚经济提升了生产力水平；但随着城市的增长，相应出现了增加的拥堵成本，进而降低了生产力水平，由此该城市每位劳动力产出为。考虑到经济体城市特征，为避免人口完全集中于某一城市，要求。此时，城市之间人口自由流动意味着城市劳动力产出水平的变化，而均衡结果意味着任意城市劳动力产出水平相等。假设任意城市都可扩充，意味着人口自由流动能使得每个城市规模发生变动。结合大数定律，在人口总量一定的情况下，要求每一位劳动力产出效率相同，此时城市均衡规模为：

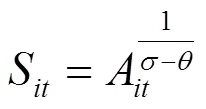
从上式可知，该模型不仅将乘数过程运用于模型中，在模型推导时也考虑了生产力变动的过程，即体现了模型加数过程。在完全自由流动假设下，人口数量为生产力的幂函数，那么城市生产力的对数正态分布反映了城市人口的对数正态分布，进一步证明了城市规模变动符合Zipf定律。

三、创新驱动与城市规模均衡

创新驱动作为城市形成理论的重要分支，近年来越来越受到关注。其中最有代表性的研究是Duranton的创新机制推进模型。[9]Duranton&Puga模型可以概括为：设定在某一城市创业需要先期支付某一初始固定成本，假定有高创新思维的创业者通过自身融资能力支付某一固定成本进入该城市，获得生产产品机会。考虑到产品生产系统性，创业者所具备的条件只够满足生产“原型产品”，即获得该产品的生产专利与技术，但并不具备满足生产该产品所需的全部资源。考虑“原型产品”生产的固定成本与可变成本之间的关系，依托城市资源获取批量生产才能够保证创业者获得足够高的生产率水平。在此前提条件下，下面来考虑产品批量化生产与城市形成之间的关系。

假设存在既定规模经济体，该经济体含有限数量投入集，包括创业者投入资源、要素生产者投入资源，其中要素生产者投入资源是创业者将原型产品转化为批量产品所必须的生产性资源条件。在此情况下，创业者创新产品生产过程实质上等同于发现原型产品与满意的生产性资源匹配的过程。在无法充分获得区域信息的情况下，创业者通过试错选择进行原型产品与生产性资源匹配，最终均衡情况为创业者原型产品的生产性资源得到满足并开展批量化生产。为此，创业者在生产性资源选择过程中存在两类策略：一类策略是当生产性资源分散分布时，创业者通过改变自身区位获得物理邻近性，同时承担迁徙成本。另一类策略是选择生产性资源集中区域，减少创业者的迁徙成本。如果生产性资源区域集中，那么不仅能减少创业者本身的迁徙成本，同时可以更好地通过区域内集聚效应为要素生产者带来便利。事实上，现实中存在大量的创业者与要素供应者同时集聚于同一区域的情况，理论界也广泛认可这种城市相处模式。但考虑到创新本身的特征会发现，创新往往是异质性资源整合的结果，异质性资源往往基于区域内资源的多样性，这与区域内同类型资源大量聚集的现实产生矛盾。

在迁移需要成本的条件下，要素生产者通过集聚提升效率的同时给创新对城市的驱动产生了另外一个问题。在试错机制存在的情况下，创业者最理想的选择情况是将自己的创业固定在一个拥有所有满足其生产要素的区域，但这并非是创业者能够直接获得的区域。从创业过程可以发现，获得创业机会需要创业者具备获得足够潜在异质性资源的可能，因此在机会搜索和获得阶段，创业者会优先选择一个具备多样性资源的区域。一旦完成选择，创业者就需要利用区域的集聚优势获得其生产效率，因此此时最优的区域应该为专业化城市。

由此，创新驱动下，在搬迁成本处在非极高或极低条件下，城市能形成一类新的均衡，该均衡反映了创业企业生命周期过程中的专业性与多样性要求。首先，创业者运用城市多样性生产结构在城市内开发新产品，发现理想资源投入结合。其次，一旦发现理想资源投入结合，此时多样性资源从区域产业布局中不能直接受益，并可能使城市规模不断增大，增加生产成本。在这种情况下不论是要素生产者还是创业者都会失去对城市多样性的兴趣。从过程角度看，对于已经掌握其理想投入要素的创业者将会选择一个具备这些资源生产者集聚的城市。也就是说，如果迁移成本并非极高，掌握其理想投入要素的创业者将会移出多样性城市，而选择一个专业化城市。因此，合理的城市分布应该是以多样性城市为基础进行创业机会的孵化，为创业者学习提供基础；而专业性的城市是创业者成熟产品生产的区域。

从Duranton&Puga的城市分布模型可以看出，在创新存在的前提下，创业者要更能利用城市的成本和资源优势，创业过程就必然对城市本身的布局有一个阶段性的把握。该研究结论也得到一些学者的证实。如在Glaeser et al.[10]以及Henderson et al.[11]的文献中，发现专业性城市在成熟产业方面更能促进企业发展；但对于高科技企业，在多样性城市中发展更加有利。另外Dumais et al.[12]以及 Bernard & Jensen[13]对于创业者进入与退出城市的问题展开了实证研究，发现在创业初期创业者选择多样性城市能较好地获得创业灵感，而一旦创业方案敲定，那么创业者选择专业化城市更利于其展开大规模的生产。

在接受创业过程影响城市分布的理论模型后，Duranton进一步探讨了创新驱动条件下城市规模的分布问题。Duranton承认，如果仅仅考察创业者对多样性和专业性城市的需求，那么合理的城市布局意味着所有城市拥有同等的规模，显然这与实际是不相符的。为使研究结论更加贴近实际，Duranton发现创新本身存在强的差异性，那么创业者对于多样性和专业性的要求也存在差异。因此，他的研究起点转向了不同城市集聚效应对不同行业的差异性影响。存在有差异的强度，那么其预测结果应该就有会差异。研究发现形成特定规模的专业化城市有赖于部门专业化水平，由于不同部门专业化存在不同的集聚效应和成本效应，因而其平衡点也不同；同时他还发现当部门在同一区域不断增长时，集聚效应随着弱化，也意味着多样性城市规模远大于专业化城市。

紧接着，Duranton开始从区位溢出的角度探讨城市规模问题。[14]他的模型建立在Romer（1990）的内生增长模型之上，其核心在于创业产品的生产受到区域溢出效应的影响。在这个模型中，Duranton假设一个区域的研究活动与该区域创业产品数量成比例。另外，他假设工人可以无成本自由流动，并且不考虑城市本身的福利情况，那么就会出现城市人口与区位产品数量成比例。在均衡状态下，不同类型的创新数量与区位人口数量成比例。但由创新导致的创业产品生产会提高对专业劳动力的需求，进而导致了人口数量的增长。这个过程类似于加数过程模型，从实质上也印证了Zipf定律。

另外，从创新角度，Duranton（2007）进一步探讨了城市规模分布机理。建立在Grossman &Helpman（1991）的熊彼特增长模型之上，Duranton提出了利润驱动模型，以反映创新产品实现过程中的新旧产品更替。在该模型中，前期创新成功意味着创业产品以其竞争优势获得垄断，跟进者如果在下一期重复对该产品创新，那么获得市场份额的概率会大大降低。因此，Duranton认为创业产品的生产需要间断，间隔化创业产品的生产由于无法扩大规模不会吸引更多的城市新进入者。值得注意的是，相邻城市的存在使各自的产品生产通过区位溢出效应进行创新思维扩散，以获得具备区位“交叉产品”的生产。在这种情况下，原有产品的生产可能发生在原有城市，但交叉产品的生产会吸引更多新进入者，相邻城市间人员实现流动从而改变城市间人口规模。Duranton针对美国城市数据发现，城市间溢出的创新使城市重新布局也符合Zipf定律。但Duranton同时指出，对于特大或者特小的城市，它们经常需要作为异常值被剔除出Zipf统计。究其原因，Duranton认为特别大的城市已经有了广泛的产品，它们无需通过区位溢出从周边获得“交叉产品”的需求。而对于一些规模很小的城市，受制于本身基础设施及发展要求等因素，本身也无法作为创新溢出源为其它城市提供“交叉产品”的生产，在这种情况下城市增长低于城市规模的比例，导致城市规模的分布呈现出与Zipf定律更小的偏度。

四、人力资本积累模型

就城市本身的增长而言，其表象为人力资本的增加。为此，一些学者单纯从人力资本的进入与流出角度分析城市的演化。Eaton & Eckstein[15]考虑了一个存在人力资本积累的集聚效应模型，认为虽然人力资本积聚主要在城市内部进行了拓展，但动态人力资本外部性是经济增长和城市存在的根基。Glaeser改进了Eaton & Eckstein的研究，将人力资本的交往由抽象的外部性简化为人力资本在不同区域间的直接交往。[16]在微观表象上，Glaeser认为学习的过程是人力资本交往的主要手段，更多工人之间的直接交往机会是知识积累和扩散的源泉，但学习仅仅发生在熟手教育新手的过程中。城市中之所以能提供学习这种交往的手段，主要原因是城市已经聚集了数量较多的熟手。新手如果想提升自己的人力资本储备，就有动机主动融入城市以结识更多的熟手。在结识熟手方面，Glaeser采用了优先连接机制，即认为新手对城市环境具有不明了性时，更愿意认识影响力更高的熟手，因此熟手被新手连接的概率与熟手本身的社会影响力（即熟手周边依附的新手数量）相关。在这种连接模式下，城市发展的格局就具备幂率特征，因而也符合Zipf统计。

人力资本积累模型的核心体现在人力资本外部性，更高人力资本积累的区域更具备吸引生手的潜质，从而扩张既有人力资本储备，因此Black & Henderson认为更大的城市规模更有利于工人提高生产率水平。[17]在更高生产率水平基础上，城市中生产者面临整体生产能力提升压力，因而迫使他们支付更多时间用于人力资本积累。在这种人力资本积累、生产效率和城市人口增长的关联下，人力资本在大城市中外部性更加显现。

但城市规模并非能够无限扩大，Aghion& Howitt提出的熊彼特视角认为城市应该被视为一类人力资本积累与城市成本的均衡。在均衡模型中，集聚力使更大的城市更具备生产力，但更多的人口数量使城市土地更为稀缺，交通等生产消费水平相应提升，造成后续跟进者无法在获得城市平均生产率水平前弥补应支付的人力资本积累成本而主动退出。[18]另外，过多竞争也使企业整体利润下降，造成经济利润丧失甚至倒闭。也就是说，在城市规模增长过程中，城市正外部性和城市成本力量交锋使城市发展到一定规模会处于停滞状态，导致城市中企业的收益与城市人口规模呈钟型曲线关系。换言之，当城市扩张时，集聚效应和城市成本效应均处于增长状态；当城市规模较小时，集聚效应占据主导；而随着城市进一步扩张，成本效应主导趋势越发显著，最终抵销集聚效应，进而限制大城市的经济增长。

五、总结

本文在当前深入推进新型城镇化背景下就城市规模的分布问题进行文献回顾，认为Zipf定律为城市规模分布提供了统计规律，为我国城市分布提供了整体性理论依据，也为其合理性诊断提供了经验手段。另外，学者们从创新驱动及人力资本积累等方面思考城市规模分布影响因素与过程，在实现机制上借鉴了古典微观经济学、熊彼特创新等经典理论，在分析范式上体现了将经典增长理论与随机理论相结合，从城市功能静态特征与人口规模动态增长相整合，在研究结论上也部分跟进了Zipf定律。虽然目前学者们对于Zipf定律的规律性和理论性探讨还在持续，但在测定城市规模分布上仍是可供实证检验的命题。

当然，我国城市规模的分布必然有其内在的特点，汲取国外理论研究的思想并借鉴国外实证研究方法只能为我国城市规模分布提供借鉴意义，而深入发掘我国城市规模的形成机理和运行机制才是摆在我国学者面前重大而深远的问题。

参考文献：

[1] Newman M E J. Power laws, Pareto distributions and Zipf'slaw[J]. Contemporary physics, 2005(5): 323-351.

[2] Rosen K T, Resnick M. The size distribution of cities: an examination of the Pareto law and primacy[J]. Journal of Urban Economics, 1980(2): 165-186.

[3] Soo K T. Zipf's Law for cities: a cross-country investigation[J]. Regional science and urban Economics, 2005(3): 239-263.

[4] Gabaix X. Zipf's law for cities: an explanation[J]. Quarterly journal of Economics, 1999(3): 739-767.

[5] Gabaix X, Ioannides Y M. The evolution of city size distributions[J]. Handbook of regional and urban economics, 2004(4): 2341-2378.

[6] Jiang B, Yin J, Liu Q. Zipf’s law for all the natural cities around the world[J]. International Journal of Geographical Information Science, 2015(3): 498-522.

[7] Simon H A. On a class of skew distribution functions[J]. Biometrika, 1955, 42(3/4): 425-440.

[8] Eeckhout J. Gibrat's law for (all) cities[J]. American Economic Review, 2004(5): 1429-1451.

[9] Duranton G, Puga D. Nursery cities: Urban diversity, process innovation, and the life cycle of products[J]. American Economic Review, 2001(5): 1454-1477.

[10] Shleifer A, Glaeser E L, Kallal H D, et al. Growth in cities[M]. National Bureau of Economic Research, 1991.

[11] Henderson J V, Kuncoro A, Turner M. Industrial development in cities[R]. National Bureau of Economic Research, 1992.

[12] Dumais G, Ellison G, Glaeser E L. Geographic concentration as a dynamic process[J]. Review of economics and Statistics, 2002(2): 193-204.

[13] Bernard A B, Jensen J B. Firm structure, multinationals, and manufacturing plant deaths[J]. The Review of Economics and Statistics, 2007(2): 193-204.

[14] Duranton G. Some foundations for Zipf's law: Product proliferation and local spillovers[J]. Regional science and urban Economics, 2006(4): 542-563.

[15] Eaton J, EcksteinZ. Cities and growth: Theory and evidence from France and Japan[J]. Regional science and urban Economics, 1997(4): 443-474.

[16] Glaeser E L. Learning in cities[J]. Journal of urban Economics, 1999(2): 254-277.

[17] Black D, Henderson V. Urban evolution in the USA[J]. Journal of Economic Geography, 2003(4): 343-372.

[18] Liu X, Derudder B, Taylor P. Mapping the evolution of hierarchical and regional tendencies in the world city network, 2000–2010[J]. Computers, environment and urban systems, 2014(1): 51-66.

（责任编校：贺常颖）

The Theory of City Development: the Literature Review

TANG Yong

（College of Urban Management; Hunan City University, Yiyang, Hunan 413000, China）

With the consideration of China’s city development this paper reviews literatures concerning with city’s scale theories. At first, this paper considers the Zipf’s law and its statistics significance in city scale, concluding its feasibility in explaining city’s development. Then, from the perspective of innovation-driven, this paper exemplifies the theory of city development, and it explores the coincidence of innovation process and city’s internal development, thinking the city is an equilibrium of “prototype production” and “mass production”; Finally, this paper reviews some literatures from human resource accumulation, and concludes that the externality of region and the externality of human resource are the main forces to drive the scale development among cities. For the three theories above, Zipf’s law can be reflected as the statistic tool, and innovation-driven and human resource accumulation can be used as the explanatory tools.

city scale; Zipf’s Law; innovation process; externality

F 291.1

A

10.3969/j. issn.2096-059X.2016.05.012

2096-059X(2016)05-0061-05

2016-06-10

湖南省社科基金项目（15JD08）；湖南省教育厅优秀青年项目（15B046）

汤勇（1978-）男，湖南益阳人，博士，副教授，主要从事区域创业管理研究。