基于酉变换-矩阵束的稀布线阵方向图综合

沈海鸥 王布宏 刘新波



基于酉变换-矩阵束的稀布线阵方向图综合

沈海鸥*王布宏 刘新波

(空军工程大学信息与导航学院 西安 710077)

该文提出一种非迭代的稀布线阵方向图综合方法。该方法首先对方向图采样数据进行centro-Hermit化处理，然后通过酉变换构造等价实矩阵束，得到非均匀单元位置与新矩阵束广义特征值的关系。在此基础上，对实矩阵奇异值分解，并舍弃非主要奇异值以获得低阶左奇异向量矩阵，进而求得稀布阵列的阵元位置和相应激励。相比于其他方法，该方法能够直接得到阵元位置的实数解，奇异值分解和特征值分解均在实数域进行，提高逼近程度的同时有效降低了计算量，仿真验证了该方法利用少量阵元即可高效实现线阵的方向图综合。

稀疏布阵；Centro-Hermit矩阵；酉变换；矩阵束；方向图综合

1 引言

近些年，阵列天线在雷达、通信、导航等方面得到了广泛应用，伴随系统功能的日益强大，天线的数目和复杂程度也随之增加，受到载体平台空间的限制，利用尽可能少的阵元数目对阵列天线进行优化布局成为阵列设计中需要解决的关键问题。阵列天线的稀疏布阵使用少于均匀等间隔布阵所需的阵元个数，在提高分辨力、抑制互耦、简化阵列结构、降低成本等方面具有明显优势[1]。根据稀疏方式的不同，可以将稀疏阵列分为两种，一种是根据稀疏率从均匀间隔阵列中抽取部分阵元得到的稀疏阵[2,3]，另一种是天线单元随机分布的稀布阵[4,5]。相比较而言，稀疏阵的阵元间距通常约束为半波长的整数倍，优化自由度较小。而稀布阵的阵元间距相互不可整除，一般大于半波长，在优化布阵过程中有更大的自由度，相同阵列孔径和阵元数条件下可以获得更优的方向图性能，近年来受到越来越多的关注。

根据给定的期望方向图，求解稀布阵列的阵元位置和相应激励，利用尽可能少的阵元个数逼近期望方向图是稀布阵列设计的主要优化目标，也是本文重点研究的内容。由于涉及较多未知变量的联合优化，使该非线性优化问题变得更加复杂，国内外学者对此展开了一系列研究。文献[6,7]利用优化算法实现稀布线阵的综合，但是对于大型阵列，智能优化算法会因为参数空间的增加导致运算量急剧增加。文献[8,9]将贝叶斯压缩感知算法成功用于求解非均匀线阵的稀疏优化综合问题，但是由于该算法的性能受到调节参数的控制，不恰当的参数选择将会严重影响算法的性能，使其适用范围受限。文献[10]通过构造方向图采样数据的Hankel矩阵，并利用矩阵束方法(Matrix Pencil Method, MPM)求解稀布线阵的阵元位置及相应激励。但是该方法涉及的矩阵运算均在复数域进行，求得的阵元位置为复数，对阵元位置的近似处理将会造成方向图逼近程度的较大误差。文献[11]在此基础上，利用前后向矩阵束算法(Forward-Backward Matrix Pencil Method, FBMPM)对复矩阵束广义特征值的分布进行约束，该方法对于非对称的赋形波束方向图综合，性能改善明显。然而这种方法无法保证所有特征值均在单位圆上，也存在某些复数阵元位置近似处理的问题，不能保证最佳的方向图拟合效果。针对上述问题，本文通过构造centro-Hermit矩阵，将其与酉矩阵相乘得到包含方向图采样信息的实矩阵，使复数域SVD和EVD问题的求解实数化，然后通过构造新的等价实矩阵束并利用稀布阵元位置与实矩阵束广义特征值的关系，直接得到稀布阵元位置的实数解，有效避免了复数阵元位置需要近似处理的问题。最后通过仿真对比验证了本文方法能够以少量阵元个数和较高的方向图拟合精度快速实现线阵的方向图综合。

2 数学模型及centro-Hermit矩阵

2.1数学模型

考虑由个全向阵元组成的线阵，阵因子可表示为

2.2 centro-Hermit矩阵

定义1[12]如果矩阵满足：

则称为centro-Hermit矩阵。其中，表示阶单位反对角置换矩阵，即

定理1[12]对于任意矩阵,是centro-Hermit矩阵。

3 稀布线阵方向图综合的酉变换-矩阵束算法

3.1算法描述

其中，

由于等价矩阵束的广义特征值相同[15]，也就是说，矩阵束左或(与)右乘任意的非奇异矩阵并不会改变矩阵束的广义特征值。对于centro-Hermit矩阵，存在阶非奇异酉矩阵：

则有

根据三角函数的二倍角公式整理式(17)，可得

将式(5)表示成矩阵形式：

3.2 实现步骤及复杂度分析

综合以上，酉变换-矩阵束算法实现稀布线阵方向图综合的具体步骤如下：

步骤1 centro-Hermit化预处理。根据期望方向图采样值计算复向量和复矩阵，然后判断是否满足式(7)，如果满足，取centro-Hermit矩阵；否则，由式(8)计算；

步骤2 计算实矩阵并进行奇异值分解。利用酉变换构造实数据矩阵。对奇异值分解，保留个左奇异向量构成矩阵；

由于矩阵束算法的计算复杂度主要由矩阵的SVD和EVD决定[13,14]，本文通过对期望方向图复采样矩阵的centro-Hermit化处理，并与酉矩阵相乘得到包含采样信息的实矩阵，使算法引入的SVD和EVD计算从复数域转换到实数域，进而通过矩阵运算得到相应的阵元位置和激励。该非迭代算法的计算复杂度可以通过估计算法主要步骤的乘法运算次数分析，根据以上步骤可知，该算法共需要次实数乘法运算，由于复矩阵乘法运算相当于同维数实矩阵乘法运算的4倍，因此，本文算法的计算复杂度约为传统矩阵束算法的1/4。

4 仿真结果及分析

4.1性能验证及分析

以文献[19]中的赋形余割方向图为期望方向图进行仿真实验，该方向图由个等间隔均匀排列的阵元实现，单元间距为半波长，峰值旁瓣电平为。对于包含方向图采样值的实矩阵，图1给出了前个奇异值的分布曲线，从图1中可以看出，当时，；当时，，且随着值增大，急剧减小。在保证获得方向图主要采样信息的情况下，通过舍弃较小的奇异值对均匀阵列进行稀疏，综合考虑稀疏率和方向图拟合程度，稀布阵列的阵元个数可在13~15间取值。稀疏率由确定，而方向图拟合程度可通过计算方向图归一化匹配误差衡量。

图2 不同M值下归一化误差关于束参数的变化趋势

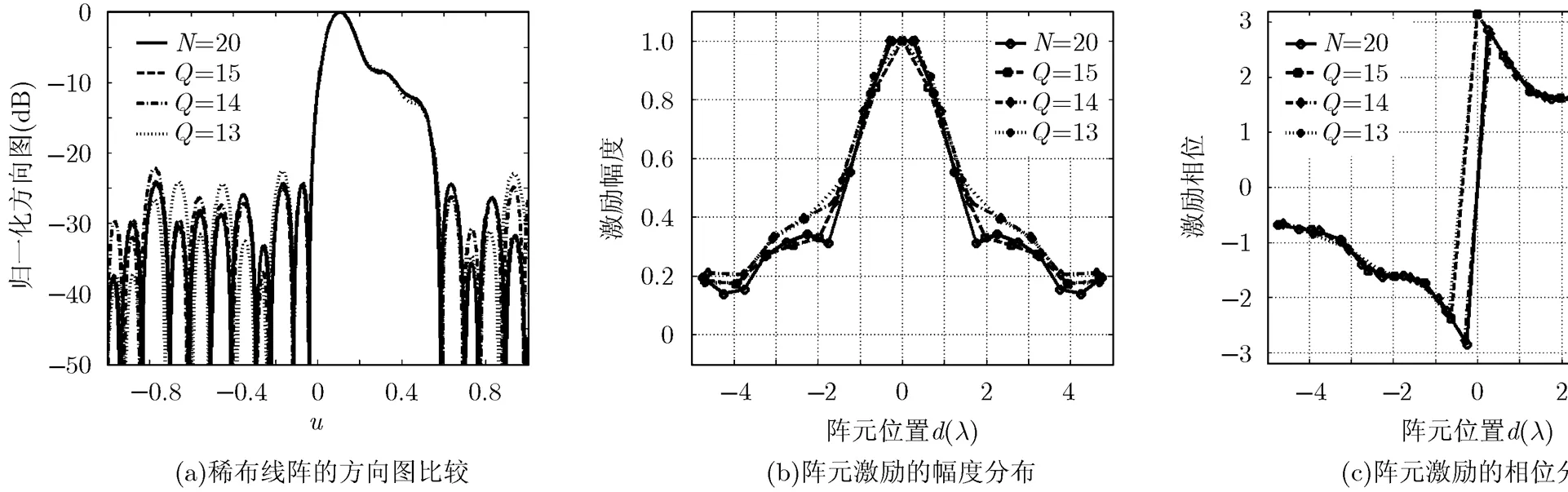
图3 不同Q值下稀布线阵的方向图及阵元位置和激励

4.2 不同算法的性能比较

为了验证算法在计算复杂度及方向图拟合精度方面的优越性，分别采用本文算法，MPM[10], FBMPM[11], BCS[8], MT-BCS[9]对个间距为半波长的单元构成的均匀线阵进行稀疏，并对相应的性能指标做以比较。以文献[20]中的余割方向图为期望方向图(CPU3.40 GHz, 3.46 GB RAM, Matlab2012b)，取=22,=121,=37进行仿真。图4给出了不同算法的方向图比较，相比于其他算法，本文算法在主瓣赋形区波束形状和副瓣电平均能满足要求的前提下，能够得到与期望方向图形状保持一致的波束方向图，可以实现方向图高精度拟合。FBMPM和MT-BCS在主瓣赋形区能够与期望方向图匹配，但是副瓣电平不能满足要求。而MPM和BCS对于本例中非对称的赋形方向图，已经不能有效地控制其波束形状。具体的性能比较见表1。表2给出了由本文方法得到稀布线阵的阵元位置及相应激励。

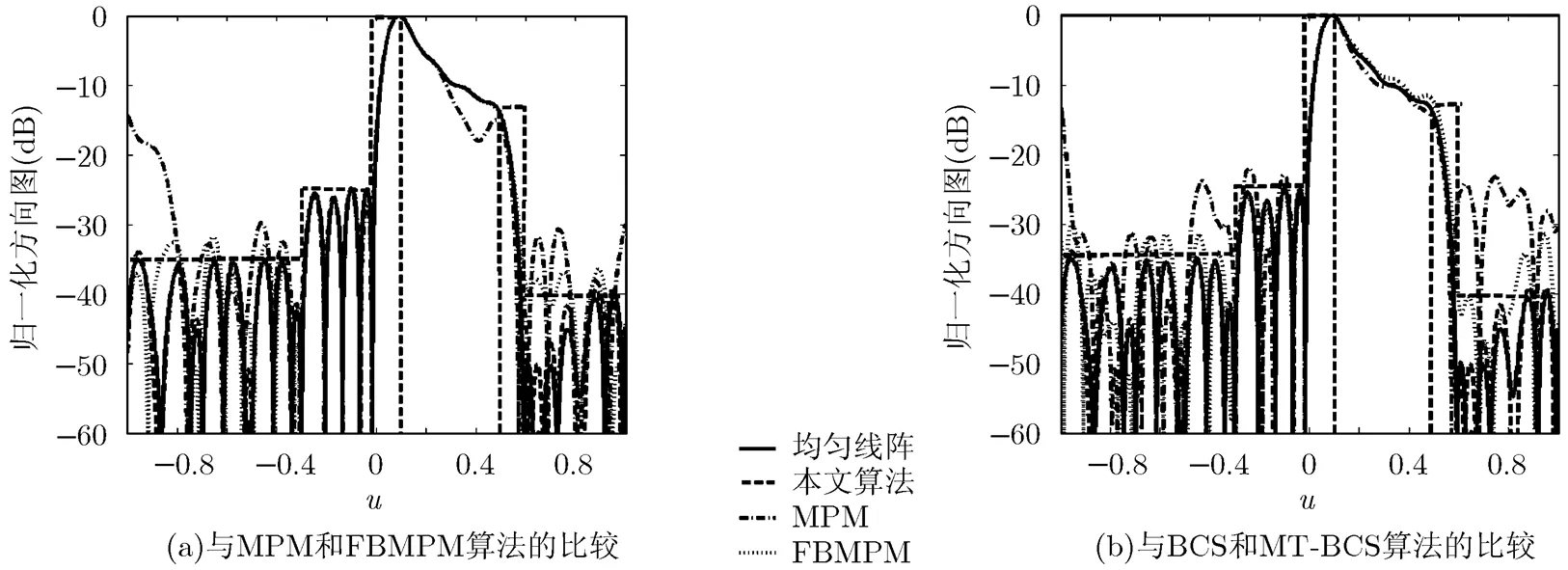
图4 不同算法的方向图比较

表1 不同算法的性能比较

表2本文算法实现稀布线阵的阵元位置和相应激励

4.3 实际天线阵列的性能及分析

为了进一步验证本文算法的可行性，引入实际天线单元进行组阵分析，通过建立如图5所示的微带贴片天线阵列模型，并利用HFSS电磁仿真软件实现全波仿真，天线的工作频率取为3.25 GHz。图5(a)是均匀阵列模型，其单元分布和激励的取值见文献[20]，图5(b)为稀布阵列模型，其单元分布和激励设置同表2。微带天线的介质基片采用厚度为2 mm的F4B-2介质板，相对介电常数为2.65，矩形贴片的长度为35 mm，宽度为26.3 mm，使用的同轴线馈电，馈电位置离贴片中心的距离为5 mm。图6给出了两个阵列全波分析的方向图，从图中可以看出，将本文算法用于实际天线阵的方向图综合，也能够实现与目标方向图波束形状的拟合，可以获得近似一致的方向图主瓣，虽然低副瓣区的拟合精度有所下降，但方向图的副瓣电平仍能满足要求，这说明本文算法同样适用于实际天线阵列。此外，为了研究单元间耦合对方向图综合性能的影响，分别将均匀阵列和稀布阵列的全波仿真方向图与其理想点源方向图进行比较，可以得到归一化匹配误差为和，这是因为与均匀阵列相比，稀布阵列的单元间距较大，实际单元的耦合对方向图性能的影响较小，使其与理想点源方向图的误差相对较小。

图5 微带贴片天线的阵列模型

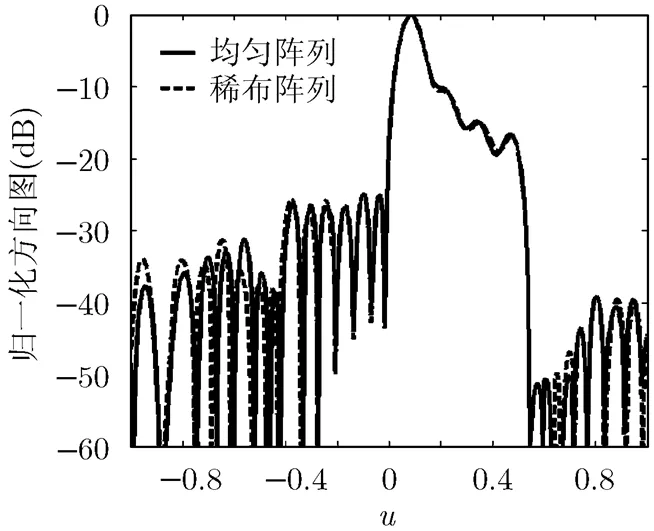
图6 全波仿真的方向图比较

5 结束语

对于稀布线阵的方向图综合，本文提出一种求解阵元位置和激励的非迭代算法。该方法利用centro-Hermit处理和酉变换将方向图复采样矩阵转变为实矩阵，使复数域的EVD和SVD问题等效到实数域。通过舍弃非主要奇异值来减少天线单元个数，再根据等价矩阵束和广义特征值分解得到稀布阵列的实阵元位置，有效解决了传统矩阵束算法求得的阵元位置需要近似处理的问题。最后仿真验证了本文方法能够快速实现稀布线阵的方向图综合，且具有计算复杂度低，拟合精度高的优点，尤其适合于阵元数目较多的大型阵列的稀疏优化。下一步的研究拟将增益和方向图拟合同时作为优化目标，根据实际应用的需要获得稀布阵列多目标联合优化的折中设计方案。

参考文献

[1] ZHAO X W, YANG Q S, and ZHANG Y H. Compressed sensing approach for pattern synthesis of maximally sparse non-uniform linear array[J].,&, 2014, 8(5): 301-307. doi: 10.1049/iet-map.2013. 0492.

[2] WANG X R, ABOUTANIOS E, and AMIN M G. Thinned array beampattern synthesis by iterative soft-threshold-based optimization algorithms[J]., 2014, 62(12): 6102-6113. doi: 10.1109/tap. 2014.2364048.

[3] SARTORI D, MANICA L, OLIVERI G,. Design of thinned arrays with controlled sidelobes by ADS-CP strategy [C]. 8th European Conference on Antennas and Propagation (EuCAP2014), Hague, Netherlands, 2014: 1-17. doi: 10.1109/ eucap.2014.6901846.

[4] PINCHERA D and MIGLIORE M D. Effective sparse array synthesis using a generalized alternate projection algorithm [C]. IEEE Conference on Antenna Measurements & Applications, Antibes, France, 2014: 16-19. doi: 10.1109/ cama.2014.7003322.

[5] 杨鹏, 闫飞, 张胜辉, 等. 基于FOCUSS算法的稀疏阵列综合[J]. 电子科技大学学报, 2014, 43(2): 203-206. doi: 10.3969/ j.issn.1001-0548.2014.02.008.

YANG Peng, YAN Fei, ZHANG Shenghui,. Sparse array synthesis based on FOCUSS algorithm[J]., 2014, 43(2): 203-206. doi: 10.3969/j.issn.1001-0548.2014.02. 008.

[6] ANGELETTI P, TOSO G, and RUGGERINI G. Sparse array antennas with optimized elements positions and dimensions[C]. 8th European Conference on Antennas and Propagation (EuCAP2014), Hague, Netherlands, 2014: 3142-3145. doi: 10.1109/eucap.2014.6902493.

[7] 贾维敏, 林志强, 姚敏立, 等. 一种多约束稀布线阵的天线综合方法[J]. 电子学报, 2013, 41(5): 926-930. doi: 10.3969/ j.issn.0372-2112.2013.05.015.

JIA Weimin, LIN Zhiqiang, YAO Minli,. A synthesis technique for linear sparse arrays with multiple constraints [J]., 2013, 41(2): 926-930. doi: 10.3969/ j.issn.0372-2112.2013.05.015.

[8] OLIVERI G and MASSA A. Bayesian compressive sampling for pattern synthesis with maximally sparse non-uniform linear arrays[J]., 2011, 59(2): 467-481. doi: 10.1109/tap.2010. 2096400.

[9] OLIVERI G, CARLIN M, and MASSA A. Complex-weight sparse linear array synthesis by Bayesian compressive sampling[J]., 2012, 60(5): 2309-2326. doi: 10.1109/ tap.2012. 2189742.

[10] LIU Y H, NIE Z P, and LIU Q H. Reducing the number of elements in a linear antenna array by the matrix pencil method[J]., 2008, 56(9): 2955-2962. doi: 10.1109/tap.2008.928801.

[11] LIU Y H, LIU Q H, and NIE Z P. Reducing the number of elements in the synthesis of shaped-beam patterns by the forward-backward matrix pencil method[J]., 2010, 58(2): 604-608. doi: 10.1109/tap.2009.2037709.

[12] LEE A. Centrohermitian and skew-centrohermitian matrices [J]., 1980, 29: 205-210. doi: 10.1016/0024-3795(80)90241-4.

[13] SARKAR T K and PEREIRE O. Using the matrix pencil method to estimate the parameters of a sum of complex exponentials[J]., 1995, 37(1): 48-55. doi: 10.1109/74.370583.

[14] KHAN M F and TUFAIL M. Comparative analysis of various matrix pencil methods for direction of arrival estimation[C]. 2010 International Conference on Image Analysis and Signal Processing (IASP), Xiamen, China, 2010: 496-501. doi: 10.1109/iasp.2010.5476066.

[15] 张贤达. 矩阵分析与应用(第2版) [M]. 北京: 清华大学出版社, 2013.11.

ZHANG X D. Matrix Analysis and Application (Second Edition)[M]. Beijing: Tsinghua University Press, 2013.11.

[16] YILMAZER N, KOH J, and SARKAR T K. Utilization of a unitary transform for efficient computation in the matrix pencil method to find the direction of arrival[J]., 2006, 54(1): 175-180. doi: 10.1109/tap.2005.861567.

[17] QIAN C, HUANG L, and SO H C. Improved unitary root-Music for DOA estimation based on pseudo-noise resampling[J]., 2014, 21(2): 140-144. doi: 10.1109/Isp.2013.2294676.

[18] LI J F and ZHANG X F. Unitary subspace-based method for angle estimation in bistatic MIMO radar[J].,, 2014, 33(2): 501-513. doi: 10.1007/s00034-013-9653-9.

[19] AKDAGLI A and GUNEY K. Touring ant colony optimization algorithm for shaped-beam pattern synthesis of linear antenna arrays[J]., 2006, 26(8): 615-628. doi: 10.1080/02726340600978349.

[20] AKDAGLI A and GUNEY K. Shaped-beam pattern synthesis of equally and unequally spaced linear antenna arrays using a modified tabu search algorithm[J]., 2003, 36(1): 16-20. doi: 10.1002/mop.10657.

Sparse Array Pattern Synthesis Using Unitary Transformation Matrix Pencil Method

SHEN Haiou WANG Buhong LIU Xinbo

(,,710077,)

A novel non-iterative method, named unitary matrix pencil method, is presented in this paper for the pattern synthesis of sparse linear arrays. Through unitary transformation of the centro-Hermit matrix constructed using sample data of the desired pattern, an equivalent real-valued matrix pencil can be achieved so as to determine the relation between non-uniform element positions and new generalized eigenvalues. Then, the lower order left singular vector matrix can be obtained by discarding the non-principal singular values generated by Singular Value Decomposition (SVD) of the real-valued matrix. The element positions and excitations are thereby estimated efficiently. Compared with other algorithms, this method can be utilized to directly obtain the real-valued solution of sparse array locations. Furthermore, Singular Value Decomposition (SVD) and Eigen Value Decomposition (EVD) are computed in the real-valued field with a lower computational cost. Simulation results validate the high-efficiency of the proposed synthesis method for the design of arbitrary linear array pattern with a fewer number of antenna elements.

Sparse array; Centro-Hermit matrix; Unitary transformation; Matrix Pencil Method (MPM); Pattern synthesis

TN820

A

1009-5896(2016)10-2667-07

10.11999/JEIT151437

2015-12-17；改回日期：2016-05-23；网络出版：2016-07-14

沈海鸥 haioushen1990@sina.com

国家自然科学基金(61172148)

The National Natural Science Foundation of China (61172148)

沈海鸥： 女，1990年生，博士生，研究方向为阵列信号处理和雷达信号处理.

王布宏： 男，1975年生，教授，博士生导师，主要从事阵列信号处理、阵列校正等方面的研究工作.