变参数细胞神经网络的分数阶可切换多元电路设计及仿真

张小红，俞梁华

（江西理工大学信息学院，江西赣州341000）

变参数细胞神经网络的分数阶可切换多元电路设计及仿真

张小红，俞梁华

（江西理工大学信息学院，江西赣州341000）

构建新的整数阶三维细胞神经网络系统，通过对其非线性动力学分析、数值计算与电路仿真，验证了该系统混沌吸引子的存在性及物理上的可实现性.同时通过调节线性参数b，研究了新的细胞神经网络系统在基于分数阶qi（i=1，2，3）不同组合条件下所表现出的混沌特性.结合分数阶电路理论分析分数阶电路中各单元电路形式，并设计了相应参数b可变、阶数值qi可切换的分数阶细胞神经网络电路系统.经统计本设计可实现13824种多元组合电路，并选取具有代表性组合电路进行电路仿真.仿真结果表明，多元电路仿真和数值仿真具有相似的混沌相图，从而证实了细胞神经网络在分数阶条件下仍表现出丰富的动力学特性，具有灵活实用价值和现实推广意义.

细胞神经网络；分数阶电路；混沌吸引子；电路仿真；可切换电路

1 引言

细胞神经网络（Cellular Neural Networks，CNN）是一种具有强实时性和连续时间动力学性质的神经网络模型，局部连接性质简单易于超大规模电路（VLSI）实现，可产生非线性动力学混沌现象甚至超混沌复杂行为. 自1988年Chua和Yang提出细胞神经网络理论［1，2］以来，CNN在预测学、图像处理、模式识别、保密通信、逻辑阵列计算机的构建等方面已经取得了巨大的发展［3，4］，具有广泛的应用前景和工程实践价值［5，6］.

分数阶微积分是研究任意阶次的微分、积分算子特性及应用的数学问题，是整数阶微积分概念的延伸和拓展［7］.近年来分数阶非线性动力学系统中存在的混沌现象也引起了人们的广泛兴趣［8］，通过对Chua混沌电路、Lorenz混沌系统以及 Chen和超混沌系统等的研究过程发现，对于整数阶的混沌系统，当阶数为分数时，系统存在更丰富的动力学特性［9，10］.利用分数阶微积分算子更能准确地描述现实世界的各种动力学特性和系统的实际物理现象.因此，对分数阶混沌系统的研究具有重要的理论研究价值.

细胞神经网络的研究至今为止大部分都是建立在整数阶的条件下，而对于其在分数阶条件下所表现出的混沌特性的研究却鲜有报道［11，12］.本文就分数阶细胞神经网络的混沌特性展开较系统的研究，在构建一个简单三维整数阶CNN系统基础上，通过理论分析、数值仿真及电路仿真，验证了该整数阶和分数阶系统混沌特性的存在性和物理可实现性，并发现改变线性参数b系统仍旧能够产生混沌吸引子现象.利用Multisim软件实现了阶数值qi可灵活切换，线性参数b可调节的分数阶CNN多元电路，电路仿真结果与数值计算具有相似的吸引子图，从而证实了本设计理论方法的正确性和现实可行性.

2 CNN系统结构及状态方程描述

细胞神经网络的基本单元电路称作一个细胞，它由线性与非线性电路元件组成，其电路原理图如图1（b）所示［13］.一个细胞神经网络系统是由相邻细胞元之间相互连接而成，图1（a）所示即为一种简单的连接方式.

C（i，j）表示第 i行、第 j列的神经元，它只同周围 r范围内的神经元相连，而同其它的神经元不连接.若用Nr（i，j）表示C（i，j）神经元和邻近其它神经元的集合，在一个m×n的二维神经元排列空间内，CNN网络的连接关系可以表示为［14］：

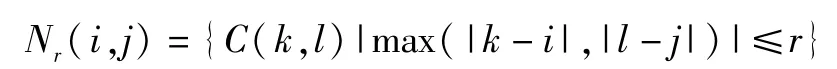
其中1≤k≤m；1≤l≤n，r为正整数.

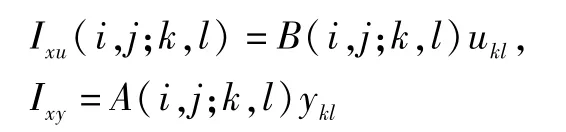
CNN中每个神经元细胞的状态可以用方程（1）来描述：

式中xij是第（i，j）个细胞的状态变量；I表示网络的外部输出；ukl（t）表示第（i，j）个细胞相应的输入电压；yu（t）是第（i，j）个细胞相应的输出，其输出函数f（xij）是一个分段线性函数，其表达式为：

为了方便起见，本文引入简化的推广CNN细胞模型，由以下无量纲的非线性状态方程描述：

其中，j为细胞标号，aj为常数，f（xj）为状态xj的输出，Go和Gs分别表示邻近连接细胞之间的状态变量和对应输出的线性组合，~Ij为门限值.

3 整数阶CNN构建、分析及电路仿真

3.1CNN系统模型构建

将式（3）中细胞神经网络推广动态模型状态方程展开，并取j=1，2，3得到本文研究的传统三阶细胞CNN模型的状态方程，其描述如下：

式中xj是第j个细胞的状态变量，f（xj）是第j个细胞相应的输出.

令系数矩阵

当初始值为x1（0）=0.1，x2（0）=0.2，x3（0）= 0.2，步长h=0.01时，对系统（5）所描述的细胞神经网络进行数值仿真，得到二维吸引子相图如图2所示.

从图2中可以看出，通过具体设定参数与初始值，系统（4）所描述的整数阶细胞神经网络中产生了双涡旋混沌奇异吸引子，因此定性的证实了该CNN系统中产生了混沌现象.

数值仿真求得系统 （4）的Lyapunov指数为（3.8651，-0.9996，-1.3355），其最大的Lyapunov指数大于 零，并 且系 统的Lyapunov维 数因此从理论上定量证明了该CNN系统中产生了混沌现象.

3.2CNN系统动力学特性理论分析

对于系统（5），由于

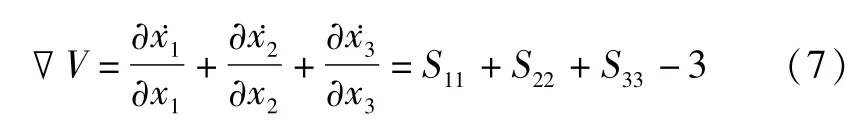
当S11=-2.43，S22=0，S33=1时，有▽V＜0，因此系统（5）是一个耗散系统，且以式（8）指数形式收敛：

即当t→∞时，系统轨线会以指数率▽V收缩到零，所有的系统轨线最终将会被限制在吸引子上，这样说明了系统吸引子的存在性.

令系统（5）中的每个微分方程右边都等于零，即

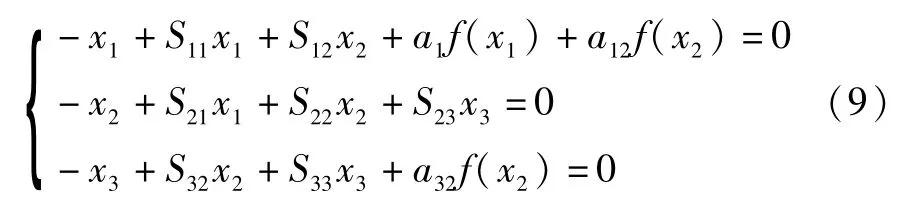
对系统（5）进行线性化处理，得到系统的Jacobi矩阵为：

由于非线性函数f（xi）的作用，对系统（5）的Jacobi矩阵求解应分组讨论，按照数学组合公式可得组合数为并对其进行分类可得如表1所示.其中“+”表示 xi≥1，“-”表示 xi≤ -1，“0”表示

对于区域Ⅰ内不难求得其平衡点为（0，0，0），Jacobi矩阵为

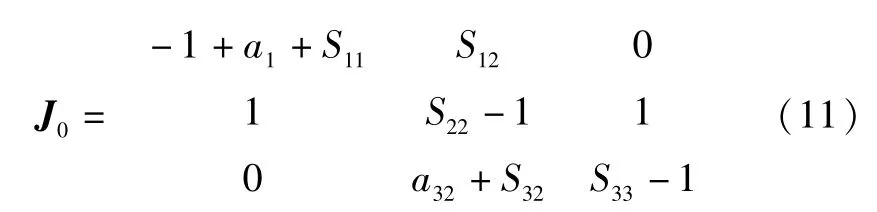
表1　f·（x1），f·（x2）取值分布

将参数值矩阵（6）代入得：

由于特征值λ2、λ3的实部为负实数，而λ1为正实数，这就意味着在（0，0，0）点是一个不稳定的且为三维空间内的一个鞍点，其不稳定性也导致了可能会产生混沌的特性.

同理也可求得其他的区域编号内的平衡点及特征值，如表2所示.该系统的平衡点都是不稳定的鞍焦点，满足Shilnikov定理［15］，即对于三阶自治系统平衡点的特征值γ和σ±ωj，若满足γσ＜0且|γ|＞|σ|，则系统的矢量场满足产生混沌的鞍焦点条件，从而在理论上证明了系统（5）存在混沌特性的可能性.

表2　各区域平衡点的特征值及其平衡点类型

3.3线性参数S22对系统的影响

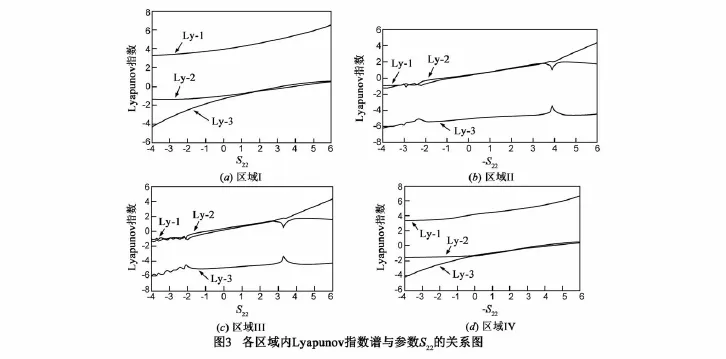
在一个动力学系统中随着系统参数值的变化，系统的平衡点和稳定性也会发生相应的变化，从而会使系统处于不同的状态.对于这种变化一般可以用Lyapunov指数谱图（图3）和分岔图（图4）直观的表示出来.对于本文中的CNN系统（5），我们仅随机选择系统中的线性参数值S22来分析其对系统的影响，若选择其它线性参数也会得到类似的结论.

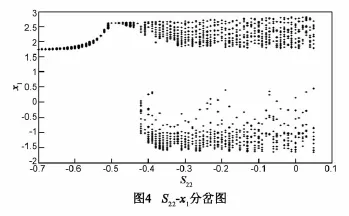
S22-x1分岔图如图4所示，从图中可以看出系统的混沌动力学行为随着S22的变化而不断改变.

3.4整数阶CNN电路仿真

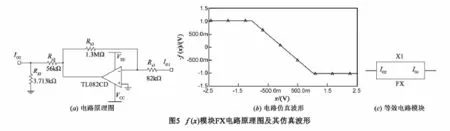
整数阶电路采用线性电阻、线性电容、运算放大器来实现.运算放大器采用 LM741来进行电路的加减运算.而对于非线性函数则用放大器TL082CD在 ±18V条件下来实现，放大电路的输出端不能直接实现 f（x）而是实现uout=-f（x），其具体的实现电路及仿真结果如图5所示.

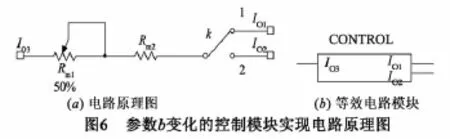
参数变化的控制模块主要由滑动变阻器和单刀双掷开关组成，其主要目的是为了实现分数阶时对线性参数b的调节，端口1和2分别对应输出x2和-x2.图中滑动变阻器选取最大值为Rm1=500kΩ，Rm2=10kΩ，电路原理图如图6所示.

依照系统（5）数学模型设计的电路原理图及其仿真结果如图7所示，电路图中各元器件的值为Rf1=Rf2=Rf3=100kΩ，R1=R2=R3=R4=R5=R6=R7=R8= R9=Ra=Rb=10kΩ，R11=29.1kΩ，R12=9.3kΩ，R13= 11kΩ，R14=66.7kΩ，R21=100kΩ，R22=50kΩ，R23= 100kΩ，R31=6.67kΩ，R32=50kΩ，C1=C2=C3=33nF.

将Multisim仿真结果与Matlab数值仿真结果比较不难发现其波形十分吻合，因此电路仿真结果是有效的，从而也验证了该混沌系统电路是可以物理实现的.

4 分数阶CNN仿真分析

4.1分数阶微积分的定义

在分数阶微积分理论发展过程中，共有若干种定义，但是最常用的是Riemann-Liouville定义的分数阶微积分，其数学表达式如下［16］：

式中的Γ（·）为Gamma函数，n-1≤q≤n，q为分数，n为整数，该式子的Laplace变换表达式为：

若函数f（t）的初始条件为零，则式（14）可表示为：

对于一个动力学系统其对应的分数阶微分方程可以表示成：

其中F（x，y）为系统输入，G（x，y）为系统输出，假设它们均满足初始值为0的条件.对其做Laplace变换，可以得到分数阶微分方程的传递函数为：

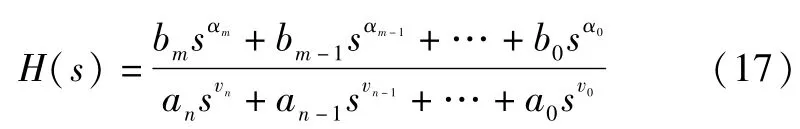
从式（15）中不难看出可以在频域中用传递函数H（s）=1/sq来表示分数阶微分算子q，因此工程中常常采用时域-复频域转换法来求解分数阶微分方程.本文3.1节通过仿真证实了传统的整数阶细胞神经网络系统（5）能够产生混沌现象，当系统的阶数值分别为q1，q2，q3（0＜q1，q2，q3＜1）时，系统（5）变为分数阶CNN系统：

当q1=q2=q3=1时退化为整数阶系统（5）.依据Charef，Hartley等研究者所提出的分数阶微积分数值解法［17］可知：当q1，q2，q3取值不同时，标准整数阶算子逐渐逼近分数阶算子的方式也不同，如表 3所示.

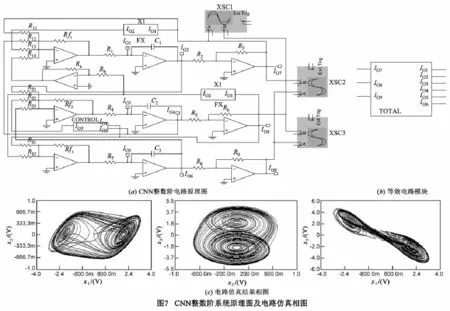
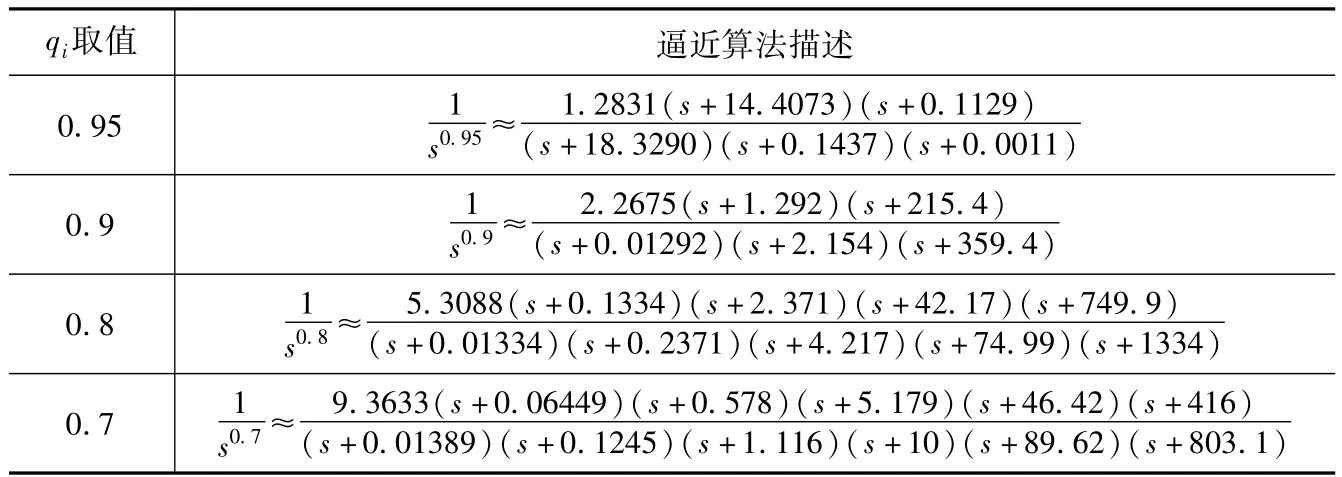
表3　整数阶逼近分数阶算子公式

4.2分数阶CNN数值仿真

将参数值矩阵（6）代入式（18）中，并令b=S22-1，则系统（18）变为

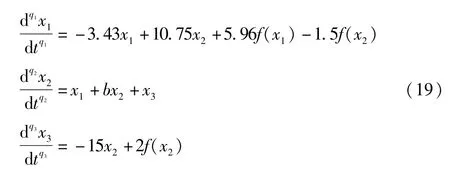
经过实验研究发现对应不同的阶数值q1，q2，q3，当改变系统（19）中的参数b时仍会表现出混沌现象.数值仿真结果如表4所示（由于篇幅有限故只选取几项进行说明）.

从表4中不难发现当分数阶CNN取不同的阶数值q1，q2，q3时，只要能够选取不同的参数值 b，就能够产生与整数阶CNN系统相似的混沌吸引子.

4.3分数阶电路单元

分数阶电路的电路单元有四种［18～20］，分别为链型、树型、混合型及新型.每种单元的电路结构如表5所示.

表5单元电路中的n为A和B之间的等效电路复频域表达式H（s）展开式中分母s的最高阶.以链型单元中q=0.95为例，A和B之间的等效电路复频域表达式为：

对应的表3可知n=3，则

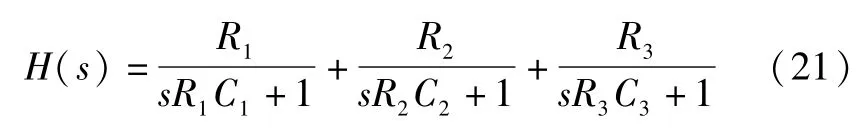
同理可求得其他类型单元电路在q=0.95时的复频域表达式，见表5.

通过对式（21）做基本的数学变形并与表3进行比较，通过比较可计算出各元件的参数值为R1=15.1kΩ，R2=1.51MΩ，R3=692.9MΩ；C1=3.616μF，C2= 4.602μF，C3=1.267μF.同理可得各个单元电路在不同q值（0.95、0.90、0.80）时各个元器件的参数值，如表6所示，其在“-”表示无元器件.

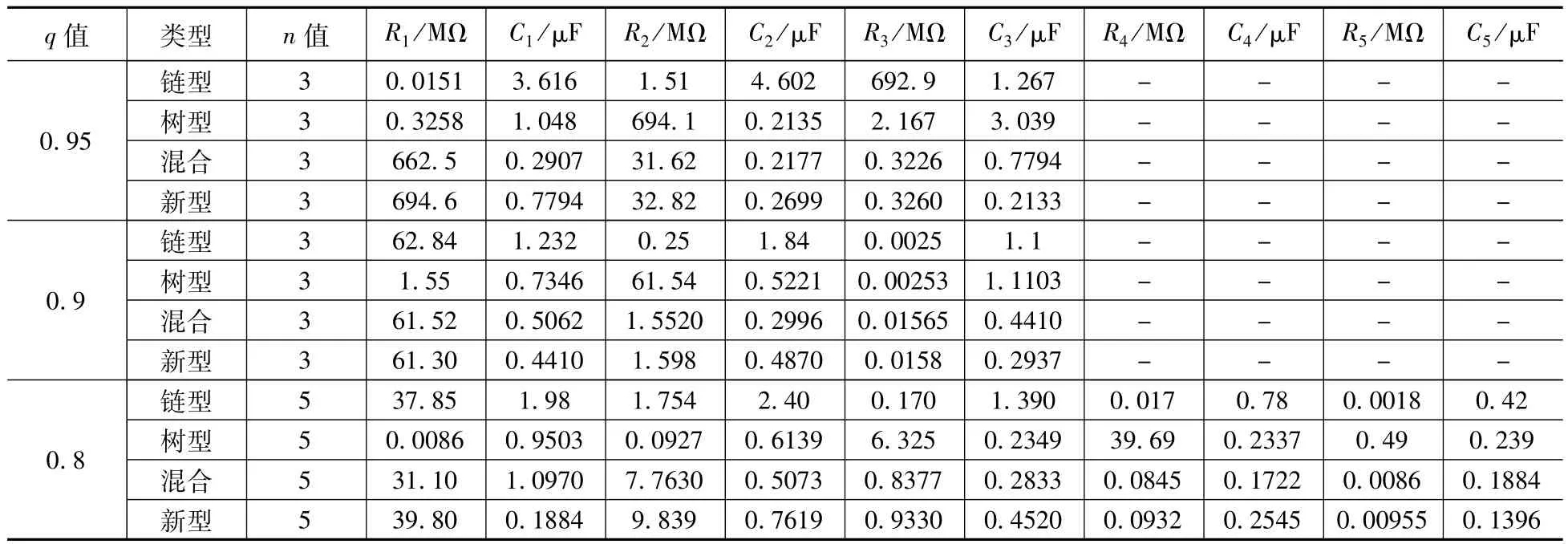
表6　分数阶各单元电路元件参数

4.4分数阶CNN电路仿真

4.4.1总体电路框图设计

在整数阶CNN系统电路原理图（图7（a））中引入分数阶电路单元，通过调节参数b来实现各阶值产生混沌现象，总体电路设计原理图如图8所示.

电路图8中的TOTAL模块即为CNN整数阶电路（图7），电路图中的电容器件C1、C2、C3由分数阶单元电路替换，LINExx，TREExx，MIXxx和NEWxx模块分别表示不同的分数阶电路单元（分别对应表5中链型、树型、混合型及新型，xx表示q值大小），实验时通过开关的闭合来控制q1，q2，q3的值.

4.4.2分数阶CNN多元电路仿真

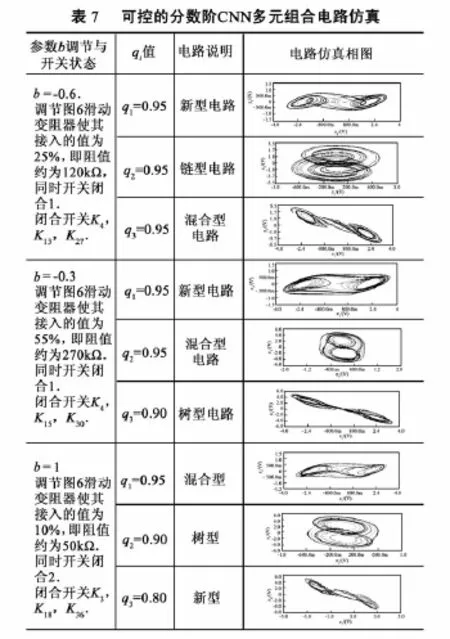
对于一个特定的三维分数阶系统，当阶值q1，q2，q3分别取电路可实现阶数｛0.7，0.75，0.8，0.85，0.9，0.95｝中任意值时，由组合数学排列原理可知共有组合方式种.由于对每一阶数值（q1，q2，q3）均有链型、树型、混合型和新型4种电路单元选择.所以对于任何一个三维的系统其电路单元设计的组合数有种.所以对于该三维的分数阶CNN系统其组合电路方式共有216×64=13824种.而对于每一种组合方式通过调节滑动变阻器改变线性参数b时，系统的混沌特性会出现相应的变化，使得系统的实际电路种数不可估量.因此对于该分数阶的系统其混沌特性更丰富.

为了简化设计而不失一般性，本文从三个阶值全部相同、不全相同和全部不同中各选择一组，所选择的阶值组合为q1=q2=q3=0.95，q1=q2=0.95，q3=0.9 和q1=0.95，q2=0.9，q3=0.8.仿真实验开关设置及实验结果如表7所示.

5 结论

研究了一个新的三维细胞神经网络系统及其在不同分数阶qi组合下的混沌动力学特性.理论分析和数值计算结果表明，所构建的新的细胞神经网络系统在整数阶及分数阶下不仅均能产生复杂的混沌动力学行为，而且具有一定的拓扑性.同时结合分数阶电路理论与多元组合电路思想，设计出参数可控的CNN可切换阶值的电路原理图.仿真结果表明电路仿真与数值仿真具有相似的混沌吸引子相图，验证了该系统理论分析的正确性及实际物理上的可实现性，该设计方法具有一定的普适性和实用推广性.

［1］L O Chua，L Yang.Celluar neural networks：Application ［J］.IEEE Transactions Circuits and System I，1988，35 （10）：1273-1290.

［2］L O Chua，L Yang.Cellularneural networks：Theory［J］. IEEE Transactions on Circuits and System I，1988，35 （10）：1257-1272.

［3］赵廷钊.基于细胞神经网络的煤仓图像处理方法的研究［J］.煤矿机械，2014，35（5）：185-186. Zhao Ting-zhao.Research on image processing method of coal bunker based on cellular neural networks［J］.Coal Mine Machinery，2014，35（5）：185-186.（in Chinese）

［4］刘泉，李佩玥，章明朝，等.基于可Markov分割混沌系统的图像加密算法［J］.电子与信息学报，2014，36（6）：1271-1277. Liu Quan，Li Pei-yue，Zhang Ming-chao.Image encryption algorithm based on chaos system having Markova portion ［J］.Journal of Electronics and Information Technology，2014，36（6）：1271-1277.（in Chinese）

［5］徐小军，王友仁.基于离散分数阶正交小波变换图像降噪新方法［J］.电子学报，2014，42（2）：280-287. Xu Xiao-jun，Wang Youren.Novel image denoising method based on discrete fractional orthogonal wavelet transform ［J］.Acta Electronica Sinica，2014，42（2）：280-287.（in Chinese）

［6］张迎迎，周立群.一类具多比例延时的细胞神经网络的指数稳定性［J］.电子学报，2012，40（6）：1159-1163. Zhang Ying-ying，Zhou Li-qun.Exponential stability of a class of cellular neural networks with multi-pantograph delays［J］.Acta Electronica Sinica，2012，40（6）：1159-1163.（in Chinese）

［7］Slavova A，Rashkova V.A novel CNN based image denoising model［A］.The 20th European Conference on Circuit Theory and Design（ECCTD）［C］.USA：IEEE，2011.226 -229.

［8］Deng S，Tian Y，Hu X，et al.Application of new advanced CNN structure with adaptive thresholds to color edge detection［J］.Communications in Nonlinear Science and Numerical Simulation，2012，17（4）：1637-1648.

［9］Caponetto R.Fractional Order Systems：Modeling and Control Applications［M］.Singapore：World Scientific，2010.

［10］孙克辉，杨静利，丘水生.分数阶混沌系统的电路仿真与实现［J］.计算机仿真，2011，28（2）：117-119. Sun Ke-hui，Yang Jing-li，Qiu Shui-sheng.Circuit simulation and implement for fractional-order chaotic systems ［J］.The Computer Simulation，2011，28（2）：117-119. （in Chinese）

［11］贾红艳，陈增强，薛薇.分数阶Lorenz系统的分析及电路实现［J］.物理学报，2013，62（14）：140503-140503. Jia Hong-yan，Chen Zeng-qiang，Xue Wei.Analysis and circuit implementation for the fractional-order Lorenz system［J］.Acta Physica Sinica，2013，62（14）：140503-140503.（in Chinese）

［12］张广军，董俊，姚宏，等.分数阶Chen混沌系统的完全同步与反向同步［J］.应用力学学报，2013，30（2）：201 -205. Zhang Guang-jun，Dong Jun，Yao Hong，et al.The complete synchronization and anti-phase synchronization of the fractional-order Chen chaotic system［J］.Chinese Journal of Applied Mechanics，2013，30（2）：201-205. （in Chinese）

［13］Chua L O，Lin G.Canonical realization of Chua’s circuit family［J］.IEEE Transactions on Circuits and System，1990，37（7）：885-902.

［14］廖晓昕.细胞神经网络的数学理论（II）［J］.中国科学（A辑），1994，24（10）：1037-1046. Liao Xiao-xi.The mathematical theory of cellular neural networks（II）［J］.China Science（A），1994，24（10）：1037-1046.（in Chinese）

［15］Silva C P.Shil’nikov’s theorem-a tutorial［J］.IEEE Transactions on Circuits and Systems I：Fundamental Theory and Applications，1993，40（10）：675-682.

［16］Podlubny I.Fractional Differential Equations：An Introduction to Fractional Derivatives，Fractional Differential E-quations，to Methods of Their Solution and Some of Their Applications［M］.USA：Academic Press，1998.

［17］A Charef，H H Sun，Y Y Tsao，B Onaral.Fractal system as represented by singularity function［J］.IEEE Transactions on Automatic Control，1992，37（9）：1465-1470.

［18］张小红，孙强.异分数阶混沌系统构造及多元电路仿真［J］.系统仿真学报，2014，26（7）：1460-1466. Zhang Xiao-hong，Sun Qiang.Construction of a heterogeneous fractional-order chaotic system and its multiple circuits simulation［J］.Journal of System Simulation，2014，26（7）：1460-1466.（in Chinese）

［19］许喆，刘崇新，杨韬.基于Lyapunov方程的分数阶新混沌系统的控制［J］.物理学报，2010，59（3）：1524 -1531. Xu Zhe，Liu Cong-xin，Yang tao.Controlling fractionalorder new chaotic system based on Lyapunov equation ［J］.Acta Physica Sinica，2010，59（3）：1524-1531.（in Chinese）

［20］曹鹤飞，张若洵.基于单驱动变量分数阶混沌同步的参数调制数字通信及硬件实现［J］.物理学报，2012，61 （2）：123-130. Cao He-fei，Zhang Ruo-xun.Parameter modulation digital communication and its circuit implementation using fractional order chaotic system via a single driving variable ［J］.Acta Physica Sinica，2012，61（2）：123-130.（in Chinese）

张小红 女，1966年8月出生，河北昌黎人.现为江西理工大学信息工程学院教授、博士、硕士生导师.研究方向为无线传感器网络、非线性动力学理论、混沌保密通信.

E-mail：xiaohongzh@263.net

俞梁华 男，1989年2月出生，江西上饶人.2013年在江西理工大学获得学士学位，现为江西理工大学硕士研究生.主要从事细胞神经网络方面的研究工作.

Multi-Element Circuit Simulation of Alterable Parameters and Switchable Fractional-Order Cellular Neural Networks

ZHANG Xiao-hong，YU Liang-hua

（Jiangxi University of Science and Technology Information Institute，Ganzhou，Jiangxi 341000，China）

Designed a new integer-order and three-dimensional cellular neural networks system.Through nonlinear dynamics analysis，numerical calculation and circuit simulation，the existence of chaotic attractor and realizability in physical about the system were verified.At the same time，studied the system’s chaotic characteristics under the conditions of different combination about fractional order qi（i=1，2，3），by adjusting the linear parameter b.According to the theoretical analysis of each unit circuit of fractional-order circuit，designed a corresponding fractional order cellular neural networks system，which has variable parameter b and switchable qi.Statically，the design can realize 13824 kinds of multiple combination circuits.This paper selects several representative combinational circuits for circuit simulation.The simulation results show that multiple circuit simulation and numerical simulation have similar chaos phase diagram，which confirmed the system still has rich dynamic characteristics under the condition of the fractional-order，also has flexible application value and realistic significance.

cellular neural networks；fractional-order circuit；chaotic attractor；circuit simulation；switchable circuit

TP391.9/O415.5

A

0372-2112（2016）04-0933-11

电子学报URL：http：//www.ejournal.org.cn 10.3969/j.issn.0372-2112.2016.04.026

2014-09-16；

2015-03-14；责任编辑：孙瑶

国家自然科学基金（No.61363076，No.11062002）；江西省自然科学基金（No.20142BAB207020）；江西省教育厅科技项目（No.GJJ14465，No.GJJ14439）；江西省研究生创新专项资金（No.YC2014-S368）