一种用于多目标定位的MIMO雷达快速功率分配算法

冯涵哲 严俊坤 刘宏伟



一种用于多目标定位的MIMO雷达快速功率分配算法

冯涵哲 严俊坤*刘宏伟

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

为了满足实际需求，该文提出一种用于多目标定位的功率分配算法，实现MIMO雷达有限功率的快速优化分配。该文首先给出了多目标定位误差的克拉美罗下界，并将其作为代价函数进行功率分配。而后，设计了一种可应用于多目标定位功率分配的交替全局优化算法，通过搜索Pareto解集来实现功率的快速分配。最后，仿真结果表明，所提的算法能快速实现MIMO雷达有限功率的优化分配，明显提升多目标定位精度。

MIMO雷达系统；克拉美罗下界；Pareto解集；交替全局优化算法

1 引言

由于实际雷达的载荷和能源总是有限的，MIMO雷达系统在对目标进行定位时发射总功率也会受到限制。因此，如何使MIMO雷达系统在有限功率约束下得到更好的目标定位性能已经成为现代研究的一个热点问题。目前，已经有越来越多的学者开始对这个问题进行研究。

从目前的现状来看，现有研究大致可分为两种框架：第1种是在MIMO雷达发射总功率恒定的前提下，调整各站的功率分布，以达到提升目标定位精度的目的[4]；第2种框架则是在保证定位精度的条件下，通过优化调整MIMO内分配方式，使得系统消耗总功率最小[5]。第1种框架为目前较常见处理框架，可通过多种优化算法来快速获取其优化结果。文献[4]在MIMO雷达背景下，研究了针对目标定位的功率分配算法[1,4,5]。为了保证系统能在各个时刻选择适当的雷达以适当的发射参数对各个目标进行正确定位，文献[6,9-12]将文献[4]的工作进行了扩展，考虑了雷达选取和功率的联合优化分配算法。但是，第1种框架缺点在于无法满足低截获的需求[8,13]。因此，按需分配的第2种框架更加贴合实际。在此框架下，普林斯顿大学学者Godrich提出了两种优化求解方法[5]。方法1是对目标函数先做凸松弛[5]后再快速求解，但松弛过程可能会引入额外误差，从而导致优化结果与最优解存在间隙；方法2是域分解方法(Domain Decomposition Methods, DDM)，该方法属于一种简化的贪婪算法，虽然可获取原问题的最优解，但庞大的计算量无法满足实时性的需求。此外，现有功率分配算法主要针对单目标的背景，在推广到多目标背景下无法使用。

针对上述问题，本文结合两种框架优势，以框架1的优化模型为主体，引入框架2的约束理念，构建了一种新的资源分配数学优化模型。具体地说，本文首先构造了一个以总功率和定位精度为优化目标的双目标函数规划(Double Objective-functions Programming, DOP)模型，实现了上文两种框架的有机结合。然后，本文结合坐标轮换和序列二次规划的思想，采用了一种交替全局优化算法(Alternating Global Search Algorithm, AGOA)对DOP模型求解。继而，结合Pareto解集理论，拟合出该DOP模型的Pareto最优曲线。进一步将本文算法通过流程的调整推广至多目标背景。最后，对提出的算法进行了有针对性的仿真，验证了本文算法在多目标背景下的有效以及单目标背景下的快速与准确性。

2 数学模型

2.1 现有的两种功率分配模型

(2)

(4)

传统针对目标定位的功率分配方法大部分按目标函数的种类，可分为如下两种：

框架1中，由于约束为线性方程，且目标函数是分式多项式，可采用多种优化方法对该框架进行求解。但在实际工程应用中，定位精度只需达到一定指标即可。采用第1种框架最终优化结果定位精度高度依赖于最初给定的，取值过小可能导致无法满足工作中的最低需求；取值过大则会造成功率浪费且与低截获的期望相矛盾。框架2则建立在按需分配的基础上，更贴近实际应用。但因为考虑到该框架中约束的复杂性，目前可以采用的优化算法较为单一，且计算时间较慢。

2.2 针对多目标定位的DOP优化模型

假设MIMO雷达采用全向发射的工作模式来实现多目标定位，此时待优化功率变量仍可表示为。同时，我们假设各个目标的观测相互独立，再将上述两种优化模型结合，可获取以总功率和定位精度为优化目标的DOP模型：

3 AGOA算法

从物理意义来讲，AGOA算法就是在固定系统发射功率将现有资源一对一注入更有优势的雷达。本文将CRLB用作AGOA算法的代价函数，采用最小可行变量集(Minimal Viable Sets, MVS)1)本文的最小可行变量集是指这些变量一起可以满足所有等式约束。轮换算法对此问题进行优化。

AGOA算法的求解过程：

从式(2)-式(4)可发现，系统定位目标的精度与雷达的发射功率、距离方位信息以及目标的RCS等都有关。式(7)是一个双目标函数的优化问题，现有的求解方法可概述为：先对原问题的子问题进行凸松弛，再通过CVX优化包对该问题求解[5]。该算法的优点是求解过程简单，但凸松弛会引入额外误差。且对于有()个目标的功率分配问题，目标函数的分子多项式是阶的，分母多项式是阶的。如果采用单目标的松弛方法得到松弛后目标函数依然是非凸的。DDM把整个问题分成多个子问题，然后求解这些子问题的的解析解；然而，当存在多目标时，我们无法找到这些子问题的解析解。

本文中，AGOA算法采用了一种新的策略进行快速计算，具体算法如下：

(2)这两个雷达站的功率的更新值记为

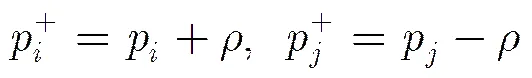
(9)

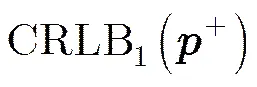
将其相加后通分可得

(11)

表1 交替全局优化算法

(1)给定初始均匀分配;(2)根据两两组合，选取其中两部雷达，其功率为，其他雷达的功率在这个子步假设是不变的，令和；(3)求解一元多项式方程，得到个根；(4)若或，去掉该根；(5)在剩余根和边界点中，找出 ，令和；(6)将用替代；(7)搜索所有的组合，完成一个扫描，令；(8)若(收敛条件取)，停止迭代。否则令，返回步骤(2)，进行下一次的搜索循环。

总起来说，由上述算法可以快速获取MIMO雷达系统的资源分配的一个折中解，继而拟合MIMO雷达的功率分配问题的Pareto集。实际应用时可以根据用户需求(定位误差、系统总功率)在得到的Pareto集曲线上选取最合适的折中解。

4 实验结果分析

为了验证了本文算法在单目标定位背景下的快速、准确性以及多目标定位背景下的有效性。本文进行了如下仿真。4.1节实验针对MIMO雷达平台设计了一种单目标定位场景，通过对比不同算法来验证本文算法的快速、准确性。4.2节实验则针对多目标定位场景进行了仿真，并验证了算法在多目标背景下的有效性。为简化仿真，假设各部发射雷达参数相同，如表2所示。

表2 发射雷达与发射信号参数

参数名称数值 信号有效带宽(MHz)1 波长(m)0.3 发射雷达最大工作功率(kW)100 发射雷达最小待机功率(kW)1

4.1 单目标背景下不同算法优化性能比较

现有功率分配优化方法，如凸松弛方法和DDM，大多仅适用单目标情况，很难推广到多目标定位情况(凸松弛方法和DDM不适合处理多目标问题)。为了能够与这些算法进行性能对比，这里设计一种单目标背景的实验，通过该仿真来验证AGOA算法的优越性。图1给出了目标与雷达的空间位置示意图。

图2在不同发射功率条件下，给出了不同优化算法得到的定位精度。结果显示，与理论分析一致，AGOA和DDM算法能够获得最优的定位精度，而松弛方法因额外误差的引入只能得到较差的定位精度。值得注意的是，当MIMO雷达系统平均的功率在15~40 kW范围内时，AGOA和DDM算法能明显提升定位性能，因为此时发射功率的可调空间较大。当功率过载或不足时(曲线两端)，两种算法的优越性不太明显。

图3给出了AGOA, DDM和凸松弛算法的优化时间。当系统总功率过载或者不足时，MIMO雷达的功率接近其发射功率的上下界，导致各站发射功率的可调空间减小，因此几种算法的优化时间都比较接近。在系统平均功率适中情况下，MIMO雷达发射功率可调整空间较大，导致DDM计算时间激增。此时，凸松弛方法具有最快的优化速度，因为该算法将代价函数松弛为线性表达式，降低了算法复杂度。结合图2的结果可以发现，AGOA算法则可以快速分配MIMO雷达的发射功率，并获取更好的定位性能。

4.2 验证算法在多目标定位背景下的有效性

为了验证算法在多目标背景下的有效性，我们设计了如下场景，MIMO雷达系统包含了4个发射雷达，3个接收雷达，目的是对4个目标进行定位，空间位置关系如图4所示。各部发射雷达信号参数如表2所示。

5 结束语

本文在分布式MIMO雷达系统下，提出了一种可应用于多目标定位的AGOA功率分配算法，将多次求解得到的结果拟合成Pareto曲线，进而使MIMO雷达系统能实时地根据各部雷达的发射参数，在功率有限等约束下达到更好的性能。具体工作方式是在各个时刻，将功率尽可能分配给优势雷达来对现有目标进行更好的定位。与传统的功率分配算法相比，本文的算法优势有如下几点：(1)直接对原函数进行优化，避免了松弛可能带来的偏差；(2)本文算法大大减少了运算时间；(3)本文算法可直接应用于多目标同时定位，更符合实际应用中可能遇到的情况。未来，推广AGOA算法，并用于解决跟踪定位一体化问题。

图1 雷达与单目标的空间位置关系  图2 多种算法对模型优化结果比较  图3 AGOA和DDM优化目标函数的优化时间

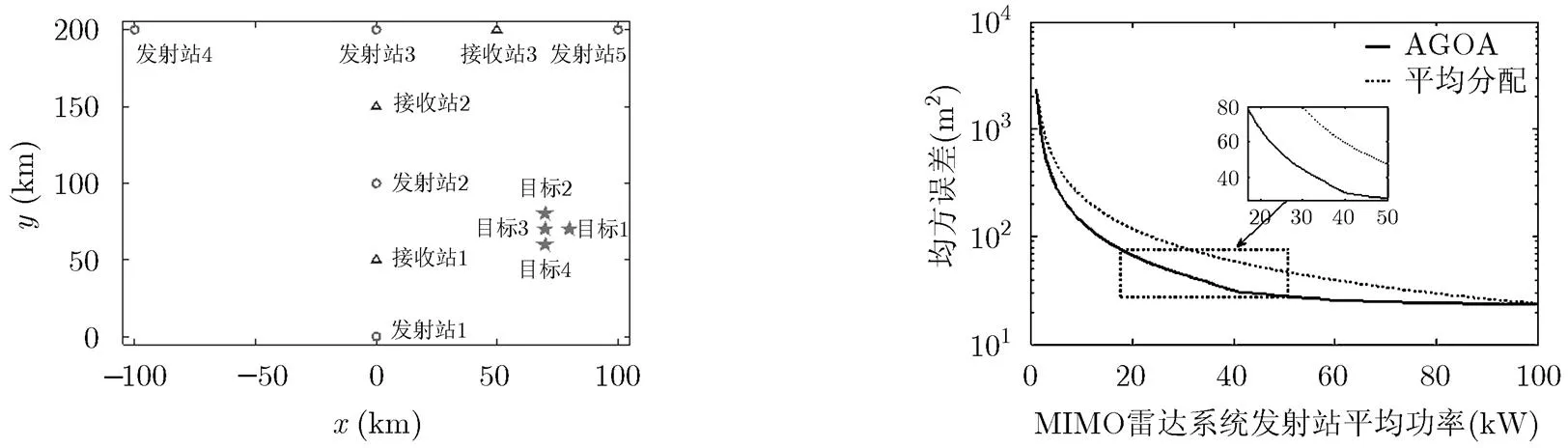
图4 MIMO雷达与4个目标的空间位置关系    图5 非起伏RCS条件下系统对多目标定位的最优解集

参考文献

[1] GODRICH H, HAIMOVICH A M, and BLUM R S. Target localization accuracy gain in MIMO radar based system [J],, 2010, 56(6): 2783-2803.

[2] VAN TREES H L and BELL K L. Bayesian Cramer-Rao bounds for multistatic radar[C]. Proceedings of Waveform Diversity Design, Orlando, FL, USA, 2007: 856-859.

[3] GODRICH H, PETROPULU A P, and POOR H V. Cluster allocation schemes for target tracking in multiple radar architectures[C]. Proceeding of Signals, Systems and Computers, Princeton, NJ, USA, 2011, 863-867.

[4] GODRICH H, PETROPULU A P, and POOR H V. Resource allocation schemes for target localization in distributed multiple radar architectures[C]. Proceedings of Signal Processing, Aalborg, Denmark, 2010: 23-27.

[5] GODRICH H, PETROPULU A, and POOR H V. Power allocation strategies for target localization in distributed multiple-radar architecture[J].2011, 59(7): 3226-3240.

[6] 严俊坤, 刘宏伟, 戴奉周, 等. 基于非线性机会约束规划的多基雷达系统稳健功率分配算法[J]. 电子与信息学报, 2014, 36(3): 509-515. doi: 10.3724/SP.J.1146.2013.01189.

YAN Junkun, LIU Hongwei, and DAI Fengzhou,. Nonlinear chance constrained programming based robust power allocation algorithm for multistatic radar systems[J].&, 2014, 36(3): 509-515. doi: 10.3724/SP.J.1146.2013.01189.

[7] 时晨光, 汪飞, 周建江, 等. 基于低截获概率优化的组网雷达系统最优功率分配算法[J]. 雷达学报, 2014, 3(4): 465-473.

SHI Chenguang, WANG Fei, and ZHOU Jianjiang,. Optimal power allocation algorithm for radar network systems based on low probability of intercept optimization[J]., 2014, 3(4): 465-473.

[8] GARCIA N, HAIMOVICH A M, COULON M,. Resource allocation in MIMO radar with multiple targets for non-coherent localization[J]., 2014, 62(10): 2656-2666.

[9] HERO A O and COCHRAN D. Sensor management: Past, present, and future[J]., 2011, 11(12): 3064-3075.

[10] VAN TREESH L. Detection, Estimation, and Modulation Theory, Part III[M]. New York, NY: John Wiley and Sons, 1971: 275-352.

[11] STOICA P and SELÉN Y. Cyclic minimizers, majorization techniques, and expectation-maximization algorithm: A refresher[J], 2004, 21(1): 112-114.

[12] GODRICH H, PETROPULU A, and POOR H V. A combinatorial optimization framework for subset selection in distributed multiple-radar architecture[C]. Proceedings of Acoustics, Speech and Signal Processing, Piscataway, NJ, USA, 2011: 2796-2799.

[13] 张娟, 赵永红, 张林让, 等. 网络化雷达协同抗干扰发射功率分配方法[P]. CN103941238A. 2014.

[14] LIN Jiguan. Multiple-objective problems: Pareto-optimal solutions by method of proper equality constraints[J]., 1976, 21(5): 641-650.

[15] KIM I Y and DE WECK O L. Adaptive weighted-sum method for bi-objective optimization: Pareto front generation [J]., 2005, 29(2): 149-158.

[16] KAO H Y, CHAN C Y, and WU D J. A multi-objective programming method for solving network DEA[J]., 2014, 24: 406-413.

[17] EHRGOTT M and WIECEK M M. Multiple Criteria Decision Analysis: State of the Art Surveys[M]. New York, NY: Springer 2005: 667-708.

冯涵哲： 男，1988 年生，博士生，研究方向为认知雷达定位、协同探测.

严俊坤： 男，1987 年生，博士后，讲师，研究方向为认知雷达、目标跟踪与定位、协同探测.

刘宏伟： 男，1971 年生，博士，教授，博士生导师，研究方向为雷达信号处理、雷达自动目标识别等.

Fast Power Allocation Algorithm for Multiple Target Localization in MIMO Radar System

FENG Hanzhe YAN Junkun LIU Hongwei

(,,710071,)

To meet the need of the real application, this paper proposes a power allocation algorithm for multiple target localization, which tries to get the quick optimal allocation of the limited power resources in the MIMO radar. Firstly, Cramér-Rao Lower Bound (CRLB) of the Mean Square Error (MSE) of the multi-target localization is given, and CRLB is used as a cost function to allocate the power resource. Then, an Alternating Global Optimal Algorithm (AGOA) is designed which can be used in power allocation of multi-target localization, the related Pareto sets to achieve the fast allocation of the power resources. Finally, the simulation results show that the AGOA can quickly achieve the optimal allocation of the limited power allocation in MIMO radar, and can significantly enhance the precision of the multiple target localization.

MIMO radar; Cramér-Rao Lower Bound (CRLB); Pareto optimal set; Alternating Global Optimal Algorithm (AGOA)

TN958

A

1009-5896(2016)12-3219-05

10.11999/JEIT160981

2016-09-29；改回日期：2016-11-23；

2016-12-14

严俊坤 jkyan@xidian.edu.cn

国家自然科学基金(61601340)，国家杰出青年科学基金(61525105)，中国博士后基金(2015M580817, 2016T90890)

The National Natural Science Foundation of China (61601340), The National Science Fund for Distinguished Young Scholars (61525105), The Postdoctoral Science Foundation of China (2015M580817, 2016T90890)