基于运动补偿的弹载前斜视SAR成像算法
2016-10-13张林让唐世阳
张 延 张林让 唐世阳
基于运动补偿的弹载前斜视SAR成像算法
张 延*张林让 唐世阳
(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)
曲线轨迹下的弹载合成孔径雷达(SAR)前视成像算法校正了方位时不变运动误差,忽略了时变运动误差,造成成像质量下降。针对这一问题,该文提出一种基于运动补偿的前斜视成像算法。首先将加速度分解成前向加速度和径向加速度,然后将径向加速度分解为成像平面内的加速度和垂直于成像平面的加速度,经过分析可知,对成像质量起决定作用的是成像平面内的加速度,该文通过矢量方法将其补偿。此外,对于加速度带来的较大的距离徙动,通过级数反演法求出信号的2维频谱,然后结合非线性频调变标(NCS)算法进行校正,取得了良好的效果。最后通过仿真实验证明了所提算法的有效性。
运动补偿;曲线轨迹;弹载;非线性频调变标算法;级数反演法
1 引言
合成孔径雷达(Synthetic Aperture Radar, SAR)由于其全天候、全天时、远距离、高精度等特点得到了广泛应用。常规SAR对两侧目标进行高分辨成像,广泛应用于对敌侦察、导弹制导等军事领域和地形测绘等民用领域。随着战场环境的日益复杂,对前向目标更为关心,而前向目标的方位维与距离维重合,形成了严重的成像盲区,因此对于前视成像的研究具有重要意义。
对于雷达前视成像,文献[5-9]提出了一种双基前视系统,在这种双基构型下,通过令雷达平台引入的多普勒信息对前向目标成像。双基构型可以有效提高被动雷达的战场生存能力,但是需要解决双基时间同步、位置同步等问题,需要较大的系统投入。文献[10-12]利用长阵列天线在垂直航向方向形成实孔径进行前视成像,由于阵列天线长度有限,分辨率往往较差,且对于导弹这一特殊雷达载体而言,对其搭载的雷达系统体积和重量等指标均有较高要求,因此这种体制需要对现有系统进行比较大的改变。文献[13]通过设计特殊的弹道,将前斜视成像模式转化为斜视工作模式,采用扩展的线频调变标(Extended Chirp Scaling, ECS)算法较好地解决了该问题,但是只考虑了加速度带来的时不变误差,忽略了时变误差,当积累时间较小时,对特定的运动参数是可行的。当运动参数改变时,成像质量变差。
因此,在曲线轨迹雷达前视成像的基础上,本文提出了一种基于运动补偿的弹载前斜视成像算法。首先在成像段通过曲线轨迹使目标与雷达运动方向保持一定的夹角,将前斜视成像模式转化为斜视成像模式,这样在不改变现有系统的条件下,实现弹载SAR的前视成像。成像过程中,加速度带来的影响必须予以补偿,本文将加速度分解成前向加速度和径向加速度,详细分析了这两个加速度与等效斜视角的关系,指出当斜视角较小时,径向加速度对成像起主要影响;斜视角较大时,前向加速度对成像起主要影响。由于本文等效斜视角较小,因此前向加速度没有考虑,只考虑径向加速度,为了更好分析径向加速度对成像效果的影响,本文将其进一步分解为成像平面内的加速度和垂直于成像平面的加速度,通过矢量分析可知,垂直于成像平面的加速度对相位误差的影响可以忽略,对成像影响起决定作用的是在成像平面内的加速度,本文通过矢量方法将其补偿。此外,对于加速度引起的较大的距离徙动,结合非线性频调变标(Nonlinear Chirp Scaling, NCS)算法对其精确校正,实现目标的精确成像。最后,通过与ECS算法的比较,验证了本文算法的有效性。
2 运动模型
本文假设导弹处于末制导阶段,已获得目标的大体方位,欲成像后选择打击位置。由于目标位于导弹航向的前下方,导引头雷达天线方位与导弹航向一致,回波的多普勒维与距离维重合,形成成像盲区,无法做合成孔径处理。也就是说,该轨迹下,仅仅利用导引头雷达无法2维分辨目标。

系数采用矢量表达式可以表示为
(2)
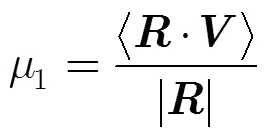
(4)
(5)
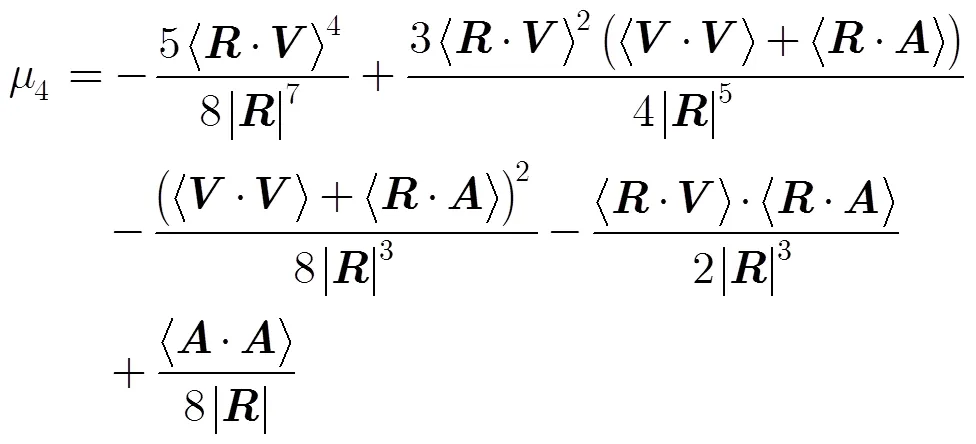
图1 导弹成像轨迹示意图
3 运动误差分析
运动误差是由导弹飞行中存在加速度造成的,从式(4)~式(6)可以看出,加速度分量存在,和中。将加速度分量代入式(1)中,忽略四阶项,得到加速度产生的运动误差在瞬时斜距中的表达式为

其中,第1项是运动误差对方位调频率的影响,第2项是运动误差对于方位高阶项的影响。为了更好地分析加速度对运动误差的影响,首先将加速度矢量分解为前向加速度和径向加速度,然后将径向加速度分解为成像平面内的加速度和垂直于成像平面的加速度,如图2所示。则运动误差的各个系数采用标量表示为
图2 加速度矢量分解示意图

(9)
(10)
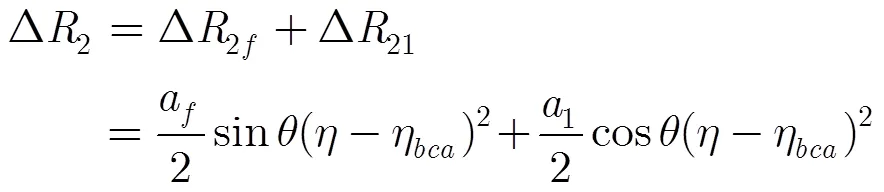
(12)
从式(11)和式(12)可以看到,加速度对调频率的运动误差由前向加速度误差分量和径向加速度误差分量组成,与加速度和等效斜视角有关;加速度对方位高阶项的误差也由前向加速度误差分量和径向加速度误差分量组成,与速度、加速度、斜距和斜视角有关。由于垂直于成像平面,所以对相位不会产生影响,没有出现在表达式中。前向加速度对成像的影响在小斜视角情况下可以忽略,因此本文主要分析径向加速度在成像平面的分量对成像的影响。由于与成正比,与成正比,因此在正侧视或者小斜视情况下,产生较大的运动误差,产生的运动误差可以忽略。也就是说,在一定的积分时间内,式(7)中的第2项在正侧视或者小斜视情况下可以忽略。为验证这个结论,选择相距中心点1000 m的,来仿真这两项运动误差引起的运动误差,仿真参数如表1所示。
表1 仿真参数

载频10 GHz 脉冲宽度10 信号带宽50 MHz PRF2000 Hz 导弹速度(500, 500, 200) m/s 导弹加速度(10, -9, -10) 导弹参考点坐标(0, 0, 9000) m 场景中心坐标(0, 10000, 0) m 积分时间0.4 s 等效斜视角8.9°
通过图3和图4可以看到,在表1的参数下,随着积分时间的增加,二次项和三次项带来的运动误差都是增加的,当积分时间小于0.4 s时,三次项引起的相位误差小于,对于成像的影响可以忽略,验证了上述分析;从图5和图6可以看到,在小斜视角情况下(约10°以下),前向加速度对成像的影响可以忽略,对成像结果起决定作用的是径向加速度,验证了上文的结论,而径向加速度的补偿也是本文算法研究的重点。
图3 二次项引起的运动误差 图4 高阶项引起的运动误差
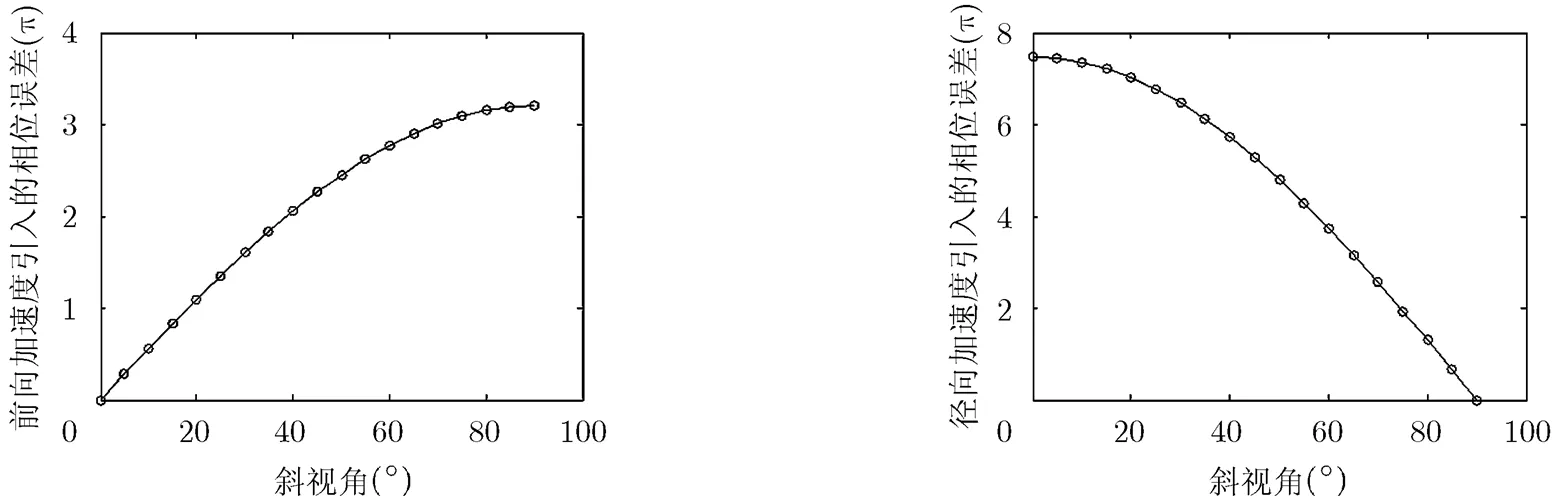
图5 二次项中前向加速度引起的运动误差 图6 二次项中径向加速度引起的运动误差
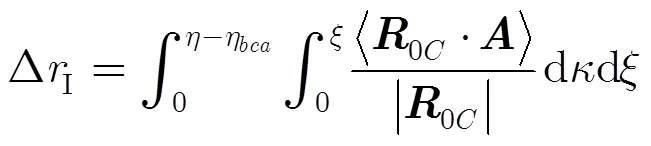
(14)
4 算法分析
本文算法流程如图7所示。距离走动补偿详见文献[13],本文在此基础上,增加距离维粗补偿:
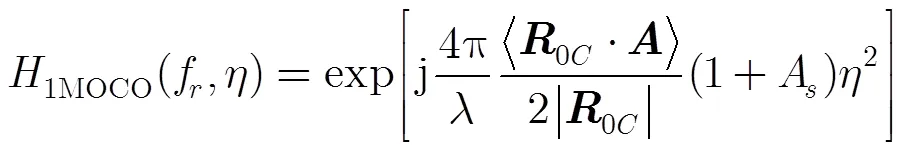
去走动和距离维粗补偿后,信号表示为
(16)

图7 算法流程

如上所述,由于雷达预先仅确定照射的范围,并不能确定目标点的确切位置。这需要对整个照射区域成像,就涉及大场景成像问题。而上述推导是针对中心点的,对于场景中偏离中心点的点,如果用上述2维频谱直接2维成像,不能完全压缩,成像质量下降,也就是没有考虑空变性,因此需要变标。在变标前,首先求出点2维谱和点2维谱之间的关系。设它们的斜距差为,则

由式(18)可以得到非线性变标因子和调频率随距离的变化率:
(19)
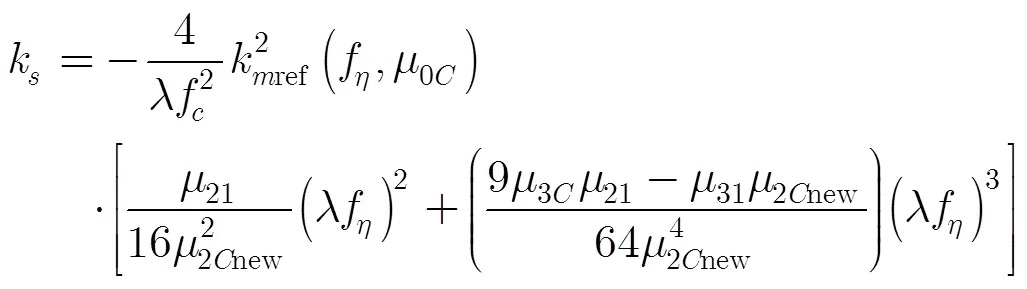
后续的处理步骤和常规NCS方法类似[15],只是在方位维处理之前需要校正运动补偿因子。
(21)
本文算法流程如图7所示。
从图7可以看到,相对于文献[13]提出的ECS算法,本文提出的NCS算法由于增加了三次相位滤波和运动补偿函数,因此需要8次傅里叶变换和7次相位函数相乘,需要的复乘次数为,其中是方位维采样点数,是距离维采样点数;ECS算法需要6次傅里叶变换和4次相位函数相乘,总的复乘次数为,两者运算量之比为,因此本文算法的运算量和ECS算法运算量在同一个数量级,差别不大,可实时成像。
5 算法仿真
为了验证该算法的有效性,将该算法与文献[13]中算法的成像结果比较。场景中心点坐标为(0, 10000, 0),边缘点和坐标分别为(0, 9000, 0), (0, 11000, 0),两者选用同样的参数,仿真参数如表1所示。
图8和图9分别给出了基于运动补偿的NCS算法成像结果和文献[13]提出的ECS算法的成像结果。为进一步说明成像质量,选择分辨率、峰值旁瓣比(Peak Side-Lobe Ratio, PSLR)和积分旁瓣比(Integrated Side-Lobe Ration, ISLR)作为衡量成像结果的指标,如表2所示。由于本文算法校正了加速度带来的时变误差,因此场景中的点目标几乎没有出现方位维散焦的状况,且方位维分辨率、PSLR和ISLR都接近理论值;ECS算法只校正了方位时不变误差,忽略了时变误差,因此场景中边缘点目标方位维主瓣展宽,旁瓣升高,主、副瓣之间耦合严重,成像效果变差。

图8 本文算法成像结果
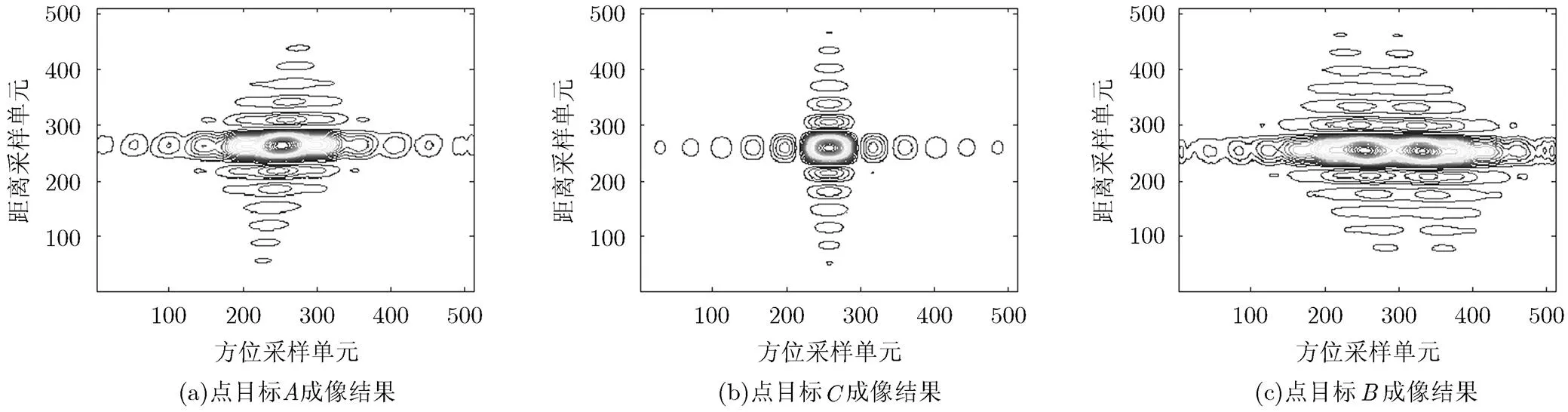
图9 ECS算法成像结果
表2 成像评估结果
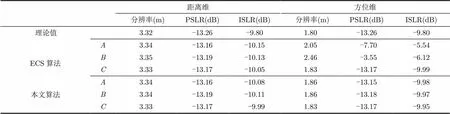
距离维方位维 分辨率(m)PSLR(dB)ISLR(dB)分辨率(m)PSLR(dB)ISLR(dB) 理论值3.32-13.26-9.801.80-13.26-9.80 A3.34-13.16-10.152.05 -7.70-5.54 ECS算法B3.35-13.19-10.132.46 -3.55-6.12 C3.33-13.17-10.051.83-13.17-9.99 本文算法A3.34-13.16-10.081.86-13.15-9.98 B3.34-13.19-10.111.86-13.18-9.97 C3.33-13.17 -9.991.83-13.17-9.95
6 结束语
本文通过曲线运动轨迹,将前斜视成像模式转化成斜视成像模式,然后分析了斜视模式下加速度的各个分量带来的运动误差对成像的影响,经分析可知,对成像效果起决定作用的是成像平面内的加速度分量,本文采用矢量方法对其进行补偿。此外,对于加速度带来的较大的距离徙动,通过级数反演法求出信号的2维频谱,然后结合NCS算法对目标进行成像,取得了良好的结果。
参考文献
[1] 庞礡, 代大海, 邢世其, 等. 前视SAR成像技术的发展和展望[J]. 系统工程与电子技术, 2013, 35(11): 2283-2290. doi: 10.3969/j.issn.1001-506X.2013.11.09.
PANG Bo, DAI Dahai, XING Shiqi,. Development and perspective of forward-looking SAR imaging technique[J]., 2013, 35(11): 2283-2290. doi: 10.3969/j.issn.1001-506X.2013.11.09.
[2] 黎剑兵, 张双喜, 苏大亮, 等. 一种多普勒域走动校正的斜视SAR成像算法[J]. 宇航学报, 2016, 37(1): 118-126. doi:10.3873/j.issn.1000-1328.2016.01.015.
LI Jianbing, ZHANG Shuangxi, SU DaliangA squint SAR imaging algorithm for linear range cell migration correction in Doppler domain[J]., 2016, 37(1): 118-126. doi: 10.3873/j.issn.1000-1328.2016.01. 015.
[3] 梁颖, 张群, 杨秋, 等. 基于改进NCS算法的弹载FMCW SAR大斜视成像方法[J]. 系统工程与电子技术, 2016, 38(8): 1764-1770. doi: 10.3969/j.issn.1001-506X.2016.08.09.
LIANG Ying, ZHANG Qun, YANG Qiu,. Study on the high squint imaging method for missile-borne FMCW SAR based on extended NCS algorithm[J]., 2016, 38(8): 1764-1770. doi: 10.3969/j.issn. 1001-506X.2016.08.09.
[4] CUMMING I G and WONG F. Digital Processing of Synthetic Aperture Radar: Algorithms and Implemention[M]. Norwood, MA: Artech House, 2005, Chapters 1-4.
[5] YI Yusheng, ZHANG Linrang, LI Yan,Range Doppler algorithm for bistatic missile-borne forward-looking SAR[C]. 2nd Asian-pacific Conference on Synthetic Aperture Radar Proceedings, Xi’an, China, 2009, 4: 960-963. doi: 10.1109/ APSAR.2009.5374268.
[6] 孟自强, 李亚超, 刑孟道, 等. 基于斜距等效的弹载双基前视SAR相位空变校正方法[J]. 电子与信息学报, 2016, 38(3): 613-621. doi: 10.11999/JEIT150782.
MENG Ziqiang, LI Yachao, XING Mengdao,. Phase space-variance correction method for missile-borne bistatic forward-looking SAR based on equivalent range equation[J].&, 2016, 38(3): 613-621. doi: 10.11999/JEIT150782.
[7] HEE S S and JONG T L. Omega-K algorithm for airborne forward-looking spotlight SAR imaging[J]., 2009, 6(2): 312-316. doi: 10.1109/LGRS.2008.2011924.
[8] LI Wenchao, YANG Jianyu, HUANG Yulin,. A geometry-based Doppler centroid estimator for bistatic forward-looking SAR[J]., 2012, 9(3): 388-392. doi: 10.1109/LGRS. 2011.2170151.
[9] 孟自强, 李亚超, 邢孟道, 等. 弹载双基前视SAR扩展场景成像算法设计[J]. 西安电子科技大学学报(自然科学版), 2016, 43(3): 31-37. doi:10.3969/j.issn.1001-2400.2016.03.006.
MENG Ziqiang, LI Yachao, XING Mengdao,. Imaging method for the extended scene of missile-borne bistatic forward-looking SAR[J].(), 2016, 43(3): 31-37. doi: 10.3969/j.issn. 1001-2400.2016.03.006.
[10] REN Xiaozhen, SUN Jiantao, YANG Ruliang,. A new three-dimensional imaging algorithm for airborne forward-looking SAR[J]., 2011, 8(1): 153-157. doi: 10.1109/LGRS. 2010.2055035.
[11] 包敏, 周鹏, 史林. 双天线前视弹载SAR解模糊算法研究[J]. 电子与信息学报, 2013, 35(12): 2857-2862. doi: 10.3724/ SP.J.1146.2013.00083.
BAO Min, ZHOU Peng, and SHI Lin. Study on deambiguity algorithm for double antenna forward looking missile borne SAR[J].&, 2013, 35(12): 2857-2862. doi: 10.3724/SP.J.1146.2013.00083.
[12] 陈琦, 杨汝良. 机载前视合成孔径雷达Chirp Scaling成像算法研究[J]. 电子与信息学报, 2008, 30(1): 228-232. doi: 10.3724/SP.J.1146.2006.00747.
CHEN Qi and YANG Ruliang. Research of chirp scaling algorithm for airborne forward-looking SAR[J].&, 2008, 30(1): 228-232. doi: 10.3724/SP.J.1146.2006.00747.
[13] 刘高高, 张林让, 刘昕, 等. 一种曲线轨迹下的大场景前斜视成像算法[J]. 电子与信息学报, 2011, 33(3): 628-633. doi: 10.3724/SP.J.1146.2010.00575.
LIU Gaogao, ZHANG Linrang, LIU Xin,. Missile-borne large region squint SAR algorithm based on a curve trajectory[J].&, 2011, 33(3): 628-633. doi: 10.3724/SP.J.1146. 2010.00575.
[14] NEO Y L, WONG F, and CUMMING I G. A two- dimensional spectrum for bistatic SAR processing using series reversion[J].2007, 4(1): 93-96.doi: 10.1109/LGRS.2006.885862.
[15] DAVIDSON G W, CUMMING I G, and ITO M R. A chirp scaling approach for processing squint mode SAR data[J]., 1996, 32(1): 121-133. doi: 10.1109/7.481254.
张 延: 男,1988年生,博士生,研究方向为机载/弹载SAR成像.
张林让: 男,1966年生,教授,博士生导师,研究方向为阵列信号处理、雷达系统仿真、雷达成像等.
唐世阳: 男,1989年生,博士生,研究方向为曲线轨迹SAR成像.
Novel Missile-borne Forward-looking SAR Algorithm Based on Motion Compensation
ZHANG Yan ZHANG Linrang TANG Shiyang
(,,’710071,)
For missile-borne forward-looking SAR in curve trajectory, time-variant motion errors are ignored, leading to degradations in imaging result. This paper proposes a missile-borne forward-looking SAR algorithm based on motion compensation to solve the above problem. The acceleration is divided into forward-looking acceleration and cross-track acceleration, the second phase error and cubic phase error caused by these two accelerations are analyzed in detail. For the cross-track acceleration component, it can be divided into the acceleration vertical to the imaging plane and the one in imaging plane further. Via such dividing, the phase errors caused by acceleration are compensated by using vectorial methods. Moreover, for range migration, it is compensated through Nonlinear Chirp Scaling (NCS) approach based on the accurate 2-D spectrum acquired by the Method of Series Reversion (MSR). The simulated results are given to illustrate the validity of the proposed algorithm.
Motion compensation; Curve trajectory; Missile-borne; Nonlinear Chirp Scaling (NCS) algorithm; Method of Series Reversion (MSR)
TN957.52
A
1009-5896(2016)12-3159-07
10.11999/JEIT161006
2016-09-30;改回日期:2016-11-24;
2016-12-14
张延 060222zhang@163.com
国家自然科学基金(61601343, 61671361)
The National Natural Science Foundation of China (61601343, 61671361)
