基于多伯努利概率假设密度的扩展目标跟踪方法

李文娟 顾 红 苏卫民



基于多伯努利概率假设密度的扩展目标跟踪方法

李文娟 顾 红*苏卫民

(南京理工大学电子工程与光电技术学院 南京 210094)

高分辨率雷达系统中，扩展目标一般会产生多个量测。现有随机有限集(RFS) 类算法一般假定扩展目标的量测数目服从泊松分布，然而这个假设与实际情况不符。针对这一问题，该文提出一种多伯努利扩展目标概率假设密度(MB-ET-PHD)跟踪算法。该算法首先假设扩展目标的量测数目服从多伯努利分布，然后通过有限集统计(FISST)理论的多目标微积分推导得到校正等式，最后给出了高斯混合(GM)框架的仿真结果。仿真结果表明该算法能够获得比泊松ET-PHD算法更好的跟踪性能。

扩展目标跟踪；概率假设密度；多伯努利

1 引言

在传统目标跟踪问题中，一个目标每个时刻最多产生一个量测。然而，在一些高分辨雷达中，一个目标会占据多个分辨单元，这种目标被称为扩展目标。在扩展目标跟踪问题中，令人感兴趣的是对扩展目标的量测数目建模。文献[1]提出扩展目标的量测数目服从泊松分布的假设，一个扩展目标产生任意数目的量测且量测互相独立。基于此假设，Mahler[2]提出一种泊松扩展目标概率假设密度(Extended Target Probability Hypothesis Density, ET-PHD)滤波算法。PHD滤波是一种新颖的随机有限集(Random Finite Set, RFS)多目标跟踪方法。与传统算法相比，PHD滤波方法易于统筹管理，避免了大量的数据关联。文献[9,10]给出了泊松ET-PHD的高斯混合(Gaussian Mixture, GM)滤波器实现方法，并提供了一种将未标记的量测集分成几个子集的方法，每个子集的所有量测应当来自同一个目标或者杂波。基于泊松ET-PHD的滤波算法，扩展目标的其他扩展信息，如形状和大小等，的建模和估计都是近年来扩展目标跟踪的研究热点。

扩展目标占据多个分辨单元，不是每个单元都能被雷达检测出量测。为了便于表述，目标占据的单元总数称为量测总数。对于静止的扩展目标，其量测总数由雷达的分辨率和目标的大小决定。每个时刻目标产生小于或者等于量测总数的量测数目。现有文献假设扩展目标的量测数目服从泊松分布，泊松分布是多伯努利分布在扩展目标的量测总数趋于无穷大，检测概率趋于无穷小的极限情况下近似得到的一种分布。然而，在实际应用中，扩展目标的量测总数有限，不可能趋于无穷大，这个扩展目标的量测数目服从泊松分布的假设显然与实际情况不符。针对这一问题，本文提出多伯努利扩展目标概率假设密度滤波(Multi-Bernoulli ET-PHD, MB-ET-PHD)算法。该算法假设扩展目标量测数目服从多伯努利分布，利用有限集统计(FInite Set STatistics, FISST)理论中的多目标微积分推导得出MB-ET-PHD的更新等式，并给出在高斯混合框架下的仿真结果。仿真实验验证了算法的有效性和比泊松ET-PHD算法更好的跟踪性能。

2 研究背景

2.1 多目标状态和量测

考虑多目标场景下的目标跟踪问题。对于多目标状态，排列无序且目标数目未知。对于接收到的量测，量测的排列是无序和随机的，且来源(杂波或者目标)未知。而多目标跟踪的目的是从未知来源和未标记的量测集中联合估计目标的数目和状态。

为了描述多目标跟踪中的不确定性，用RFS表示多目标状态集和量测集，其中，和分别是所有子集和的集合，目标和量测数目分别为和。是时刻的第个目标的运动状态矢量，和分别是目标的位置坐标和速度信息，是时刻的第个量测矢量，是量测在笛卡尔坐标系下的坐标信息。

2.2 泊松ET-PHD滤波器

对于扩展目标跟踪问题，现有PHD滤波算法假设扩展目标的量测数目服从泊松分布。与传统滤波算法相同，泊松ET-PHD滤波算法分为预测等式和更新等式。假设存活概率和检测概率与目标状态无关，即，那么时刻的泊松ET-PHD滤波预测等式和更新等式[9,10]分别为

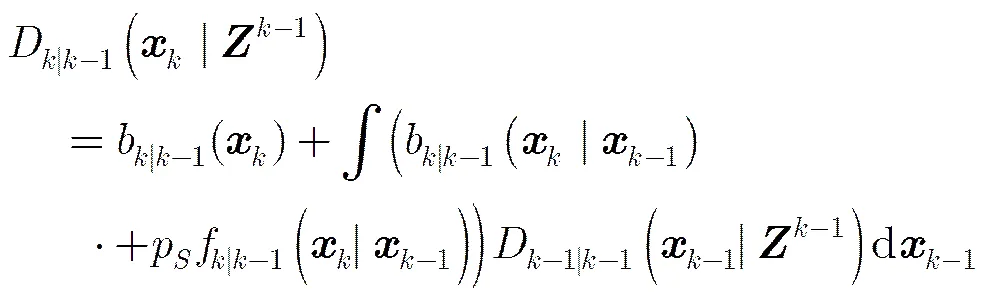
(2)

为了更好地理解式(2)，假设某一时刻的量测集只有3个元素。那么，最多存在5种分类情况，分别为

(4)

2.3 量测数目模型

与扩展目标的量测数目模型不同，杂波的量测数目应该假设服从泊松分布。跟踪场景的每个分辨单元都有可能检测出杂波。一些高分辨雷达的分辨单元总数可达到108的数量级，每个分辨单元的虚警概率又很小。当很大，概率很小时，两者的乘积是一个常值，这是多伯努利分布的一种极限情况，称为泊松分布。因此，可以假设杂波的量测数目在空间上服从泊松分布。

然而，现有泊松ET-PHD滤波算法假设扩展目标的量测数目服从泊松分布，这显然与实际情况不符。因为与整个跟踪场景的分辨单元数相比，每个扩展目标占据的分辨单元有限，不可能趋于无穷大。所以，假设扩展目标的量测数目服从泊松分布是不妥的。

为了对扩展目标和杂波的量测数目建模，引入RFS理论中一个重要的基本统计描述符：概率生成泛函(Probability Generating Functional, PGFL)。假设是状态空间上的多目标RFS，那么的PGFL定义[3]为，其中，是随机有限集的概率密度函数，是关于矢量的检测函数。当，；否则，。

多伯努利分布的PGFL[3]为，其中，,是关于矢量的检测函数，是扩展目标的量测总数。泊松分布的PGFL[3]为，其中是期望平均量测数目。

3 MB-ET-PHD滤波算法推导

由于MB-ET-PHD滤波算法的预测等式与泊松ET-PHD相同，见式(1)，下面仅讨论更新步骤的公式推导。

引理1

(8)

引理2

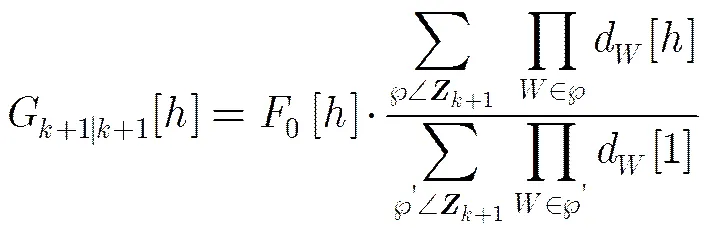
(10)

证明 根据文献[3]，多扩展目标的校正等式的PGFL是

将式(6)代入式(11)即可得到引理2。 证毕

定理1 MB-ET-PHD的更新等式为

证明 对式(9)求导，得到

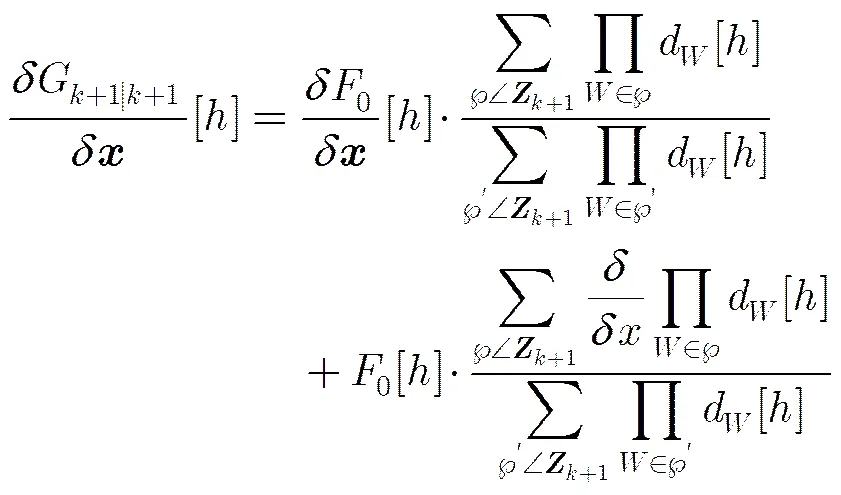
(14)

将PHD的量测更新[3]代入式(15)，可得定理1。定理1的隐含条件为，为了保证阶乘的非负性，用取代中的，即

(16)

4 实验结果与分析

实验1和实验2分别在线性系统和非线性系统下比较本文算法和泊松ET-PHD的目标估计数目和最佳子模式分配(Optimal SubPattern Assignment, OSPA)距离误差。两种滤波器保持真实航迹数据和算法参数不变，蒙特卡罗仿真100次，每次仿真的观测数据独立产生。假设存活概率和检测概率与目标状态无关，即，检测概率。实验1和实验2均采用ET-PHD滤波的高斯混合实现方法，高斯分量的修剪阈值，合并阈值，以及最大分量数目。其中，实验2采用不敏卡尔曼(Unscented Kalman, UK)和PHD相结合的滤波器进行仿真实验。

实验1考虑线性系统的多目标运动场景 线性系统的动态方程和量测方程分别为和。其中，表示采样时刻，是系统转移矩阵，是过程噪声，其协方差为是量测矩阵，是量测噪声，和是2维的单位矩阵和全零矩阵，采样间隔s,和分别是过程噪声和测量噪声的协方差，过程噪声的标准差m/s2，测量噪声的标准差m/s2。在一个[-1000 1000] m×[-1000 1000] m的2维仿真场景中，目标运动的最大时间为100 s。杂波强度为,m-2。场景中目标的新生和死亡发生在不同的时间和地点，场景中最多同时存在10个目标，目标的轨迹如图1所示。分别有8个目标与其他目标空间邻近，目标两两邻近，且邻近的两个目标量测总数分别为10和30，具体如下：从第41 s到80 s，两个目标平行同向运动，任意时刻纵坐标只相差10 m。在第51 s和第64 s，目标轨迹发生交叉。在第71 s，产生一个衍生目标。衍生目标的强度为，其中，。剩余目标的量测总数均为10。新生目标的强度为

其中,

假设在整个运动过程中，每个目标的量测总数不随时间变化。量测、真实目标位置和MB-ET-GM- PHD滤波器的估计值如图2所示。滤波估计结果表明MB-ET-GM-PHD滤波算法能够正确跟踪多个目标。为了更好地评估本文算法，实验1分别在不同杂波强度、不同检测概率以及时变的量测总数情况下比较本文算法与泊松ET-GM-PHD滤波算法的跟踪性能。

假设每个目标的量测总数保持不变，检测概率为0.9。当杂波强度不同时，两种算法的目标估计数目和OSPA误差距离如图3所示(从上到下，相应的杂波数目分别是10, 30, 50)。可以发现以下几点：(1)随着杂波强度不断增大，MB-ET-GM-PHD算法的目标数目估计和OSPA误差几乎不受影响。相反，泊松ET-GM-PHD算法的OSPA误差距离有小幅度的增长；(2)除目标空间邻近时刻外，两种算法的跟踪性能相差不大；(3)当不同大小的目标空间邻近时，MB-ET-GM-PHD算法的目标数目估计更为准确，OSPA误差更小。

假设每个目标的量测总数保持不变，杂波数目为10，图4给出了两种滤波算法在不同检测概率下的目标数目估计和OSPA误差距离。可以看出，当两个大小不一的目标靠的很近时，不管检测概率如何变化，MB-ET-GM-PHD算法的跟踪性能总是比泊松ET-GM-PHD算法好；当检测概率从0.9降低到0.7时，两种滤波算法的OSPA误差幅度变化不大；当检测概率较低(0.5)时，两种滤波算法的目标数目估计和OSPA距离均增大。究其原因，这两种滤波算法都依赖于目标的量测数目，当检测概率较低，检测到的属于目标的量测数目较少，从而导致两种滤波算法的跟踪性能降低。

图1线性系统的目标真实轨迹        图2 量测、真实目标位置和本文算法的估计值

图4 线性系统不同检测概率下两种算法的跟踪性能对比

在实际应用中，目标的量测总数随着时间不断变化，与目标的径向距离和目标的大小有关。对于一个确切的目标，它的量测总数只跟径向距离有关，即。检测后的量测数目小于或者等于量测总数，其量测数目是随机的，相应的平均期望是量测总数和检测概率的乘积。为了清楚明白地展示两种算法在量测总数随时间不断变化时的跟踪性能，只选择跟踪在第64 s交叉的两个目标。这两个目标轨迹不同，但任意时刻的径向距离和量测总数均相同。两个目标分别运行100 s，随径向距离变化的量测总数函数为

两种算法的目标数目估计和OSPA距离如图5所示。可以看出，当两个大小相同的目标相距较远时，两种算法都能够获得准确的目标数目估计和相差不大的OSPA距离。在两个大小相同的目标空间邻近时刻附近，两种算法均高估目标的数目，这是合乎情理。因为，当两个目标靠的很近而且量测总数相同时，每个目标对应的高斯分量有两个较大权值，滤波器无法取舍，从而高估目标数目。

目标的真实轨迹如图6所示，目标运动的最大时间为50 s。，目标的起始位置和终止位置分别用圆圈和方形表示。场景中最多同时存在6个目标，在第30 s两个大小不一的目标相遇，其量测总数分别是10和20。其余目标目标的量测总数为20。

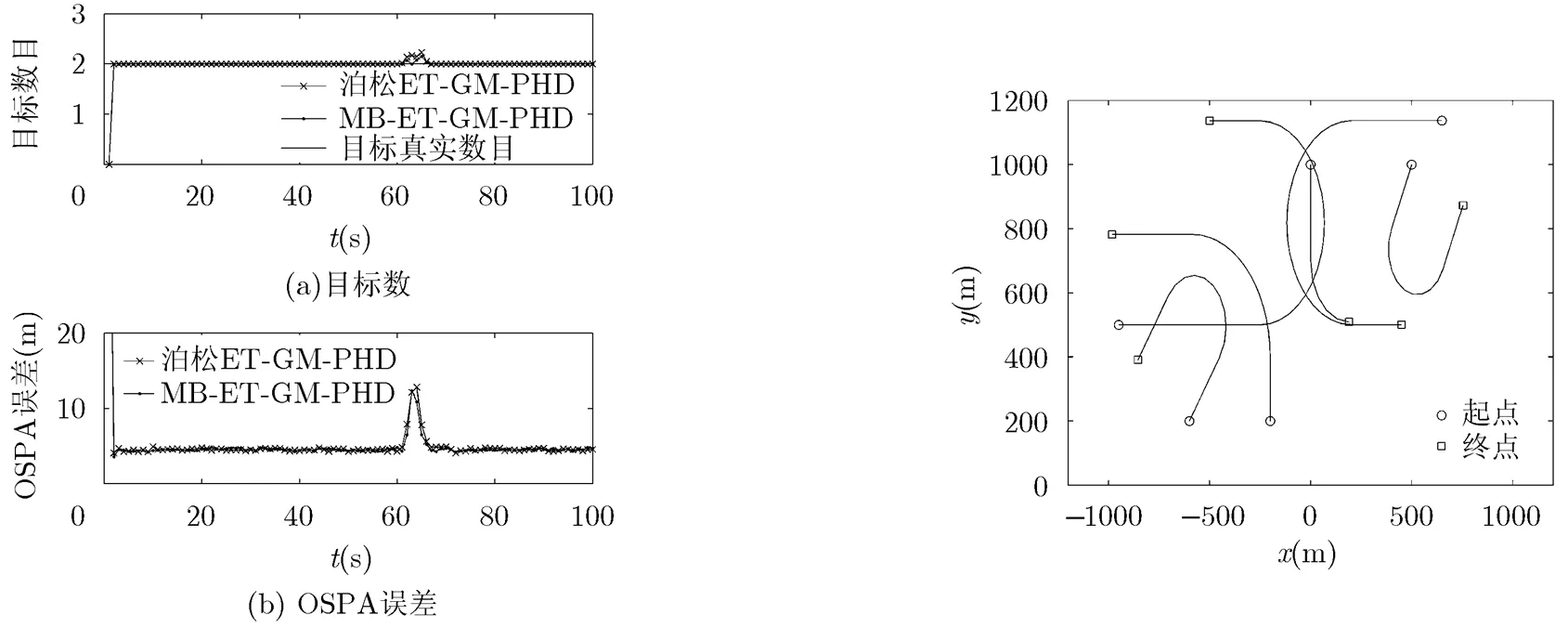
图5 线性系统下量测总数时变时两种算法的跟踪性能       图6 非线性系统的目标真实轨迹

假设没有衍生目标，新生目标的强度为

图7 非线性系统不同杂波强度下两种算法的OSPA距离  图8 非线性系统不同检测概率下两种算法的OSPA距离

事实上，两种算法唯一不同的是校正器(式(2)和式(12))，算法复杂度相差不大。在杂波数目为10，检测概率为0.9且目标的量测总数不变的条件下，MB-ET-GM-PHD算法和泊松ET-GM-PHD算法在线性系统下的蒙特卡罗平均运算时间分别是15.79 s和15.97 s，在非线性系统下的蒙特卡罗平均运算时间分别是3.47 s和3.30 s。综合实验1和实验2，可以得出以下结论：不论线性系统还是非线性系统，对于空间邻近的不同大小的目标，MB-ET- GM-PHD算法的跟踪性能比泊松ET-GM-PHD的更好。对于相隔较远的多目标、空间邻近的相同大小的目标或者量测总数时变的目标，在相同的检测概率和杂波强度下，MB-ET-GM-PHD算法和泊松ET-GM-PHD的跟踪性能差距不大。

5 结束语

针对现有扩展目标量测数目的泊松模型与实际情况不符的问题，本文提出了一种基于新的量测数目模型的MB-ET-PHD滤波算法。该算法通过引入多伯努利分布对扩展目标的量测数目建模，利用FISST多目标微积分和PHD滤波器推导得到MB-ET-PHD的更新等式。仿真结果表明，相比于泊松ET-PHD多目标跟踪算法，MB-ET-PHD算法的目标数目估计更为准确，OSPA距离误差更小，跟踪空间邻近目标的能力更强。

参考文献

[1] GILHOLM K and SALMOND D. Spatial distribution model for tracking extended objects[J].,&, 2005, 152(5): 364-371.doi: 10.1049/ip-rsn: 20045114.

[2] MAHLER R. PHD filters for nonstandard targets I: extended targets[C]. International Conference on Information Fusion, Seattle, WA, USA, 2009: 915-921.

[3] MAHLER R. Statistical Multisource-Multitarget Information Fusion[M]. Artech House, Norwood, MA, 2007: 193-360.

[4] MAHLER R. Multi target Bayes filtering via first-order multi target moments[J]., 2003, 39(4): 1152-1178.doi: 10.1109/ TAES.2003.1261119.

[5] VO B, SINGH S, and DOUCENT A. Sequential Monte Carlo methods for multi-target filtering with random finite sets[J]., 2005, 41(4): 1224-1245.doi: 10.1109/TAES.2005.1561884.

[6] 胡子军, 张林让, 张鹏, 等. 基于高斯混合带势概率假设密度滤波器的位置杂波下多机动目标跟踪算法[J]. 电子与信息学报, 2015, 37(1): 116-122. doi: 10.11999/JEIT140218.

HU Zijun, ZHANG Linrang, ZHANG Peng,. Gaussian mixture cardinalized probability hypothesis density filter for multiple maneuvering target tracking under unknown clutter situation[J].&, 2015, 37(1): 116-122.doi: 10.11999/JEIT140218.

[7] 吴卫华, 江晶, 冯讯, 等. 基于高斯混合势化概率假设密度的脉冲多普勒雷达多目标跟踪算法[J].电子与信息学报, 2015, 37(6): 1490-1494.doi: 10.11999/JEIT141232.

WU Weihua, JIANG Jing, FENG Xun,. Multi-target tracking algorithm based on Gaussian mixture cardinalized probability hypothesis density for pulse Doppler radar[J].&, 2015, 37(6): 1490-1494.doi: 10.11999/JEIT141232.

[8] VO B and MA W. The Gaussian mixture probability hypothesis density filter[J]., 2006, 54(11): 4091-4104.doi: 10.1109/TSP.2006. 881190.

[9] GRANSTROM K, LUNDQUIST C, and ORGUNER U. Extended target tracking using a Gaussian mixture PHD filter[J]., 2012, 48(4): 3268-3286.doi: 10.1109/TAES.2012. 6324703.

[10] GRANSTROM K, LUNDQUIST C, and ORGUNER U. A Gaussian mixture PHD filter for extended target tracking[C]. International Conference on Information Fusion, Edinburgh, Scotland, UK, 2010: 1-8.doi: 10.1109/ICIF.2010.5711885.

[11] LAN Jian and LI Xiaorong. Tracking of maneuvering non-ellopsoidal extended ojectct or target group using random matrix[J]., 2014, 62(9): 1042-1059.doi: 10.1109/TSP.2014.2309561.

[12] FELDMANN M, FRANKEN D, and KOCH W. Tracking of extended objects and group targets using random matrices[J]., 2011, 59(4): 1409-1420.doi: 10.1109/TSP.2010.2101064.

[13] GRANSTROM K and ORGUNER U. A PHD filter for tracking multiple extended targets using random matrices[J]., 2012, 60(11): 5657-5671.doi: 10.1109/TSP.2012.2212888.

[14] GENNARELLI G, VIVONE G, BRACA P,. Multiple extended target tracking for through-wall radars[J]., 2015, 53(12): 6482-6494.doi: 10.1109/TGRS.2015.2441957.

[15] WAHLSTROM N and OZKAN E. Extended target tracking using Gaussian processes[J]., 2015, 63(16): 4165-4178.doi: 10.1109/TSP. 2015.2424194.

[16] GRANSTROM K, NATALE A, BRACA P,. Gamma Gaussian inverse Wishart probability hypothesis density for extended target tracking using X-band marine radar data[J]., 2015, 53(12): 6617-6631.doi: 10.1109/TGRS.2015.2444794.

[17] BEARD M, REUTER S, GILHOLM K,. Multiple extended target tracking with labeled random finite sets[J]., 2016, 64(7): 1638-1653.doi: 10.1109/TSP.2015.2505683.

[18] MA Dongdong, LIAN Feng, and LIU Jing. Sequential Monte Carlo implementation of cardinality balanced multi-target multi-Bernoulli filter for extended target tracking[J].,&,2016, 10(2): 272-277.doi: 10.1049/iet-rsn.2015.0081.

李文娟： 女，1990年生，博士生，研究方向为场面监视雷达信号处理、目标跟踪与识别.

顾 红： 男，1967年生，教授，博士生导师，主要研究方向为雷达信号处理、噪声雷达体制、稀疏阵列信号处理.

苏卫民： 男，1959年生，教授，博士生导师，主要研究方向为阵列信号处理、雷达成像.

Extended Target Tracking Method Based on Multi-Bernoulli Probability Hypothesis Density

LI Wenjuan GU Hong SU Weimin

(,,210094,)

Extended targets usually generate multiple measurements in high resolution radar systems. Existing algorithms of the Random Finite Set (RFS) assume that the measurement number of extended targets follows Poisson distribution in a general way. However, this assumption is inconsistent with actual situations. Considering this issue, a Multi-Bernoulli Extended Target Probability Hypothesis Density (MB-ET-PHD) tracking method is proposed. First, this method assumes that the measurement number of extended targets is Multi-Bernoulli (MB) distributed. Then, its update equation is derived by using the FInite Set STatistics (FISST) multi-target calculus. Finally, simulated results of Gaussian Mixture (GM) framework are given. The simulation results show that the proposed method can obtain better tracking performance compared with the Poisson ET-PHD method.

Extended target tracking; Probability Hypothesis Density (PHD); Multi-Bernoulli (MB)

TN953

A

1009-5896(2016)12-3114-08

10.11999/JEIT160372

2016-04-18；改回日期：2016-08-25；

2016-10-21

顾红 guhongjust@163.com

国家自然科学基金(61471198)

The National Natural Science Foundation of China (61471198)