基于贝塞尔函数基信号分解的微动群目标特征提取方法

张 群 何其芳 罗 迎



基于贝塞尔函数基信号分解的微动群目标特征提取方法

张 群 何其芳*罗 迎

(空军工程大学信息与导航学院 西安 710077) (信息感知技术协同创新中心 西安 710077)

微动特征提取是群目标分辨的有效手段，以往针对孤立目标的特征提取技术不再适用。针对此该文提出了一种基于信号分解的微动群目标特征提取方法。首先通过分析微动信号的正弦调频(SFM)形式，推导了SFM信号相位项在-分辨率贝塞尔函数基上的分解结果；然后根据回波分解结果中微动频率与函数基的一一对应关系进行频率粗略估计，并针对误差产生原因给出了精确的微动频率估计方法；最后在离散信号相位解模糊的基础上，完成各子目标的微动频率提取。仿真实验验证了算法的有效性，且与正弦调频傅里叶变换(SFMFT)算法和平均幅度差函数(AMDF)算法相比具有更高精度。

微多普勒；群目标；贝塞尔函数基；特征提取；参数估计

1 引言

当多个目标位于雷达天线同一波束范围内，目标回波信号在时频域相互叠加构成群目标[1,2]。群目标特征提取旨在利用目标的不同参数和特征实现群目标分辨与识别[3]。微多普勒效应(micro-Doppler effect, m-D effect)反映了目标的精细运动特征[4,5]，不同目标的微多普勒特征往往各不相同。对于地面驻停车辆群，可通过提取发动机的振动微多普勒特征分辨汽车与坦克，还可根据发动机转速来区分不同发动机类型；对于中段弹道导弹群目标，可通过提取目标进动微多普勒特征进行真弹头的识别。因此，基于微多普勒效应的目标特征提取是实现群目标分辨识别的有效途径之一。

近年来，国内外学者对微多普勒特征提取技术进行了大量的研究。一类主要的方法基于联合时频分布(Joint Time-Frequency Distribution, JTFD)展开，此类方法不需要建立参数化模型，在计算微动回波JTFD的基础上寻找周期性特征进行特征提取。然而，不同JTFD方法在时频分辨率、鲁棒性和计算复杂度等方面各具优劣，同时此类方法往往参数估计精度不足。为此，文献[9]提出一种基于分段FFT的瞬时频率估计算法，该算法的估计精度有所提高，但FFT分段长度对不同信号的估计精度存在影响。文献[10]提出一种基于时变自回归(Time-Varying Auto-Regressive, TVAR)模型的参数估计方法，该方法能够准确地估计微动参数并提取目标几何尺寸。平均幅度差函数(Average Magnitude Difference Function, AMDF)法是一种参数化估计方法，对噪声不敏感且易于实现[11,12]。然而，以上微动特征提取技术的研究对象均为孤立目标，对于群目标不再适用。

针对微动群目标，文献[13]提出一种基于时频滤波和Viterbi算法的微动信号分离方法。文献[14]通过对APY-6SAR数据的分析，指出微动信号为正弦调频(Sinusoidal Frequency-Modulated, SFM)形式，基于此，一类在正交基函数上进行SFM信号分解投影，并通过变换域信号进行微动特征提取的方法发展起来。文献[15]通过将微动信号相位项的调制信息正交投影在三角函数基上，提出了一种基于正弦调频傅里叶变换(Sinusoidal Frequency Modulation Fourier Transform, SFMFT)的微动群目标参数估计方法。该方法通过SFMFT计算可得到微动信号频谱，然而，频谱中除真实频率谱线外还存在干扰项谱线。与SFMFT采用的三角函数基不同，傅里叶-贝塞尔变换(Fourier-Bessel Transform, FBT)将信号投影在贝塞尔函数上，免除了干扰项，使得线性调频信号能够很好地在贝塞尔函数域上完成分离。基于这种考虑，本文结合-分辨率贝塞尔函数基的性质，通过研究微动信号的SFM形式，在分析SFM信号相位项在贝塞尔函数基上分解结果的基础上，提出了一种微动群目标参数估计算法。

2 贝塞尔函数性质分析

经典的信号表示方法通常将信号投影在正交基上，这类方法一般能够较好地反映信号在时域难以表现的特征，如小波变换、Fourier变换等。为清楚地阐释贝塞尔函数与信号的关系以及相关计算的物理意义，现将部分贝塞尔函数性质分析如下。

2.1 准周期性

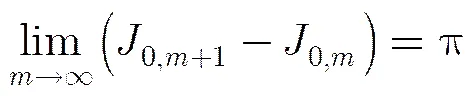
(2)

2.2 幅值特性

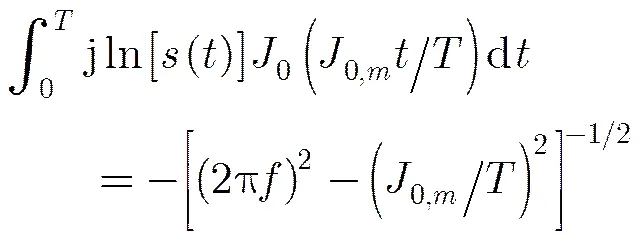
由式(3)可知，该信号在贝塞尔函数基上的投影的幅值大小仅随项数改变。当时幅值取得最小值，则该最小值项数与频率存在一一对应关系。因此，若信号投影在第项贝塞尔函数时取得最小值，表明与之对应的SFM信号理论调制频率为。

2.3 贝塞尔函数基分辨率

有限时域SFM信号与贝塞尔函数基进行投影，等价于将信号的频率调制成分依次分解在各项贝塞尔函数基上。由于贝塞尔函数与理论调制频率一一对应，若将相邻两项贝塞尔函数基进行等分，以等分后的函数基进行信号分解，则第项函数对应的理论调制频率为

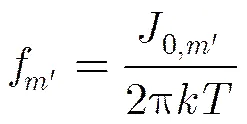
3 参数估计相关分析

当SFM信号调制指数超过一定范围时，离散SFM信号的参数估计受相位模糊的影响[15]，本文所提算法也同样存在这一问题。为获得更加精确的估计频率，同时避免由相位模糊造成的估计错误，现对估计误差以及相位模糊产生的原因进行分析，并在此基础上给出相应修正方法。

3.1 估计误差分析

则有

(6)

由基本不等式性质，解得

(8)

3.2 相位模糊分析

4 微动群目标回波分析与估计算法

本节分别以自旋群目标和振动群目标为例，推导微动群目标回波的SFM形式，并在回波SFM形式的分析基础上，以多分量SFM信号为模型给出微动群目标的参数估计算法。

4.1 微动群目标回波分析

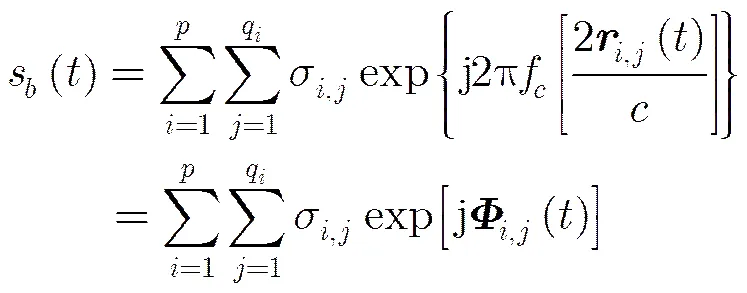
市售3种富马酸替诺福韦二吡呋酯片的主要质量比较……………………… 田慈惠，刘航岐，杨 柳，等（3·175）

(11)

联立式(10)至式(12)，对相位项求导得到的微动频率为

(13)

4.1.2 振动群目标 在相同雷达体制信号下进行振动群目标微多普勒效应分析。假设某振动目标群包含个子目标，目标上存在个散射点且均以相同频率进行周期性振动。散射点的振幅为,和分别为振动轴与雷达所形成的方位角和仰角。当目标群位于雷达远场时，振动定向轴的方位角和仰角可近似为和，则时刻散射点到该目标参考点的距离为

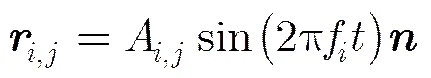
(15)

由式(15)可知，振动群目标的微多普勒频率同样按正弦规律变化。综上所述，自旋群目标和振动群目标的微动回波信号均为SFM形式，表现为具有不同调制指数和调制频率的多分量SFM信号的叠加，这与文献[14]的分析相符。

4.2 参数估计算法

下面以微动群目标离散回波信号为模型给出具体的参数估计算法。由4.1节分析可知，由自旋和振动引起的微动回波信号为SFM形式，则以序列长为的多分量SFM离散信号建立微动群目标回波信号模型。

(16)

式中信号分解结果为虚部项与实部项之和。仅考察实部项：

(18)

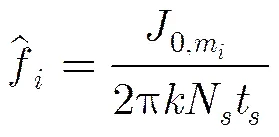
其中，

(20)

综上所述，基于贝塞尔函数基信号分解的微动群目标参数估计算法流程为：

步骤 2 判断回波信号是否存在相位模糊。若存在，则对回波信号进行相位解模糊处理；

步骤 3 计算回波信号与贝塞尔函数基的投影，取最小幅值对应项数，计算初始估计频率；

步骤5 重复步骤3–步骤4，直到不存在明显的最小幅值项。

5 仿真实验

为分析算法有效性，对本文算法与AMDF算法及文献[15]提出的SFMFT算法，从参数估计精度和鲁棒性两方面进行分析与比较。

5.1 算法精度与鲁棒性分析

图1表明，无论在是否含有噪声的条件下，信号分解投影的幅值分别在,和处取得极小值。将,和分别代入式(19)~式(21)，求解得3个振动子目标的估计频率分别为3.2345 Hz, 7.9345 Hz和13.1345 Hz，估计频率误差均在0.0300 Hz以内。可见，本文算法在SNR>0 dB时能够较好地进行微动群目标的频率估计。

归一化均方误差(Normalized Root-Mean- Square Error, NRMSE)是衡量参数估计精度的常用指标，它表征了估计参数与实际参数之间的欧氏距离。为分析SNR与-分辨率对估计精度的影响，本文采用200次Monte Carol仿真，以3个子目标估计频率的NRMSE平均值衡量算法的估计精度，仿真结果如图2所示。

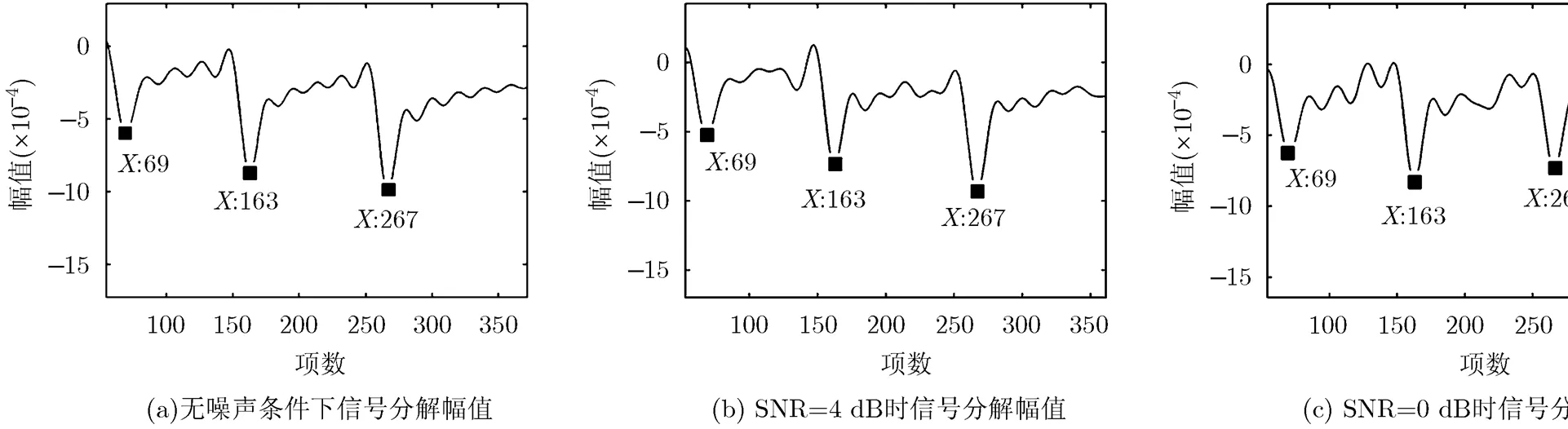
图1 采用k-分辨率贝塞尔函数基信号分解结果

图2 不同SNR及k-分辨率条件下频率估计的NRMSE

5.2 算法对比分析

SFMFT算法[15]通过定义信号的正弦调频空间，将微动信号的相位项调制信息直接投影在以三角函数构成的正交基上，并以频谱的形式表达出来。以相同振动群目标为模型，在不同SNR条件下采用SFMFT算法进行仿真，仿真结果如图3所示。

图3(a)表明，即使在无噪声条件下，除过在3个子目标的微动频率,处外还含有若干项谱线，这些谱线将对微动特征的提取造成干扰；图3(b)与图3(c)表明，在时，SFMFT频谱仍能够反映各子目标的振动频率，但干扰项同样存在。

AMDF算法[11,12]将采样序列采用加窗处理，通过信号时移、作差、绝对值求和等一系列运算，寻找谷值点求取微动周期。下面采用AMDF算法进行目标的微动频率估计，仿真实验结果如图4所示。

图4(a)表明，基于AMDF的微动参数估计算法不适用于微动群目标，当若干信号分量叠加在一起时谷值点将产生混乱。图4(b)与图4(c)分别为在和条件下以目标1为例的仿真结果。从图上可以看出，在0 dB和条件下基于AMDF的参数估计算法能够通过谷值点较好地反映单目标的振动周期与振动频率，经计算其估计误差分别为0.0096 Hz和0.0319 Hz。

由3种算法的仿真实验结果可以看出，SFMFT算法和AMDF算法均在低SNR条件下具有更强的鲁棒性。然而，SFMFT算法在对群目标微动频率估计时干扰项较为明显，而AMDF算法无法对群目标回波进行微动频率估计。为得到一般性的结论，现将以上3种算法的主要指标进行对比总结，如表1所示。

图3 SFMFT算法仿真得到的振动群目标估计频谱

图4 基于AMDF的微动目标特征提取算法仿真图

表1 算法主要指标对比

SFMFT算法AMDF算法贝塞尔函数基信号分解算法 是否适用于群目标参数估计是否是 是否含干扰项是否否 参数估计精度(Hz)约为 关键参数信号序列长信号序列长，时延窗长信号序列长，k-分辨率 最低信噪比约为-4 dB约为-4 dB约为0 dB

综上所述，3种算法的估计精度同样受限于脉冲重复频率与信号序列长。对于相同的PRF和信号序列长，文中算法具有更高的估计精度，理论上可通过选取合适的-分辨率贝塞尔函数基来达到估计精度要求，且对群目标进行微动频率估计时不存在干扰项；然而，该算法相比前两种算法对噪声更为敏感，通常适用于SNR>0 dB的条件。

6 结束语

参考文献

[1] 黄剑, 胡卫东. 基于贝叶斯框架的空间群目标跟踪技术[J]. 雷达学报, 2013, 2(1): 86-96. doi: 10.3724/SP.J.1300.2013. 20079.

HUANG Jian and HU Weidong. Tracking of group space objects within Bayesian framework[J]., 2013, 2(1): 86-96. doi: 10.3724/SP.J.1300.2013.20079.

[2] 李靖卿, 冯存前, 张栋, 等. 基于时频域增强和全变差的群目标信号分离[J]. 北京航空航天大学学报, 2016, 42(2): 375-382. doi: 10.13700/j.Bh.1001-5965.2015.0110.

LI Jingqing, FENG Cunqian, ZHANG Dong,Group-target signal separation based on time-frequency enhancement and total variation[J]., 2016, 42(2): 375-382. doi: 10.13700/j.Bh.1001-5965.2015.0110.

[3] 关永胜, 左群声, 刘宏伟. 高噪声环境下微动多目标分辨[J]. 电子与信息学报, 2010, 32(11): 2630-2635. doi: 10.3724/SP. J.1146.2009.01348.

GUAN Yongsheng, ZUO Qunsheng, and LIU Hongwei. Micro-motion targets resolution in a high noise environment[J].&, 2010, 32(11): 2630-2635. doi: 10.3724/SP.J.1146. 2009.01348.

[4] CHEN V C, LI Fayin, HO Shenshyang,. Micro-Doppler effect in radar: Phenomenon, model and simulation study[J]., 2006, 42(1): 2-21. doi: 10.1109/TAES.2006.1603402.

[5] NARAYANAN R M and ZENALDIN M. Radar micro- Doppler signatures of various human activities[J].,&, 2015, 9(9): 1205-1215. doi: 10.1049/iet- rsn.2015.0173.

[6] THAYAPARAN T, ABROL S, RISEBOROUGH E,. Analysis of radar micro-Doppler signatures from experimental helicopter and human data[J].,&, 2007, 1(4): 288-299. doi: 10.1049/iet-rsn: 20060103.

[7] QI Wang, PEPIN M, BEACH R J,. Demonstration of target vibration estimation in synthetic aperture radar imagery[C]. 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, Canada, 2011: 4083-4086. doi: 10.1109/IGARSS.2011.6050130.

[8] 陈小龙, 刘宁波, 王国庆, 等. 基于高斯短时分数阶Fourier变换的海面微动目标检测方法[J]. 电子学报, 2014, 42(5): 971-977. doi: 10.3969/j.issn.0372-2112.2014.05.021.

CHEN Xiaolong, LIU Ningbo, WANG Guoqing,. Gaussian short-time fractional Fourier transform based detection algorithm of target with micro-motion at sea[J]., 2014, 42(5): 971-977. doi: 10.3969 /j.issn.0372-2112.2014.05.021.

[9] QU Wenxing, YANG Wenge, and ZHANG Ruoyu. Frequency estimation method of sinusoidal frequency signal based on piecewise FFT[C]. 11th International Conference on Wireless Communications, Networking and Mobile Computing, Shanghai, China, 2015: 1-4. doi: 10.1049/cp.2015.0638.

[10] 韩勋, 杜兰, 刘宏伟. 基于窄带微多普勒调制的锥体目标参数估计[J]. 电子与信息学报, 2015, 37(4): 961-968. doi: 10.11999 /JEIT140814.

HAN Xun, DU Lan, and LIU Hongwei. Parameter estimation of cone-shaped target based on narrowband micro-Doppler modulation[J].&, 2015, 37(4): 961-968. doi: 10.11999/JEIT140814.

[11] 王玥, 钱志鸿, 张营. 基于扩展谱相减的RCAF基音周期检测算法[J]. 电子与信息学报, 2009, 31(5): 1161-1165.

WANG Yue, QIAN Zhihong, and ZHANG Ying. RCAF pitch detection algorithm based on expanded spectral subtraction [J].&, 2009, 31(5): 1161-1165.

[12] 王义哲, 冯存前, 李靖卿, 等. 弹道导弹群防御目标信号识别仿真研究[J]. 计算机仿真, 2016, 33(1): 42-46.

WANG Yizhe, FENG Cunqian, LI Jingqing,. A study on simulation of group-target signal identification in ballistic missile defense[J]., 2016, 33(1): 42-46.

[13] LI Po, WANG Dechun, and WANG Lu. Separation of micro- Doppler signals based on time frequency filter and Viterbi algorithm[J].,, 2013, 7(3): 593-605.

[14] SPARR T and KRANE B. Time-frequency analysis of vibrating targets in airborne SAR system[J].-,, 2003, 150(3): 173-176. doi: 10.1049/ip-rsn:20030447.

[15] PENG Bo, WEI Xizhang, DENG Bin,. A sinusoidal frequency modulation Fourier transform for radar-based vehicle vibration estimation[J]., 2014, 63(9): 2188-2199. doi: 10.1109/TIM.2014.2308031.

[16] PACHORI R B and SIRCAR P. A new technique to reduce cross terms in the Wigner distribution[J]., 2007, 17(2): 466-474. doi: 10.1016/j.dsp.2006. 10.004.

[17] SURESH P, THAYAPARAN T, and VENKATARAMANIAH K. Fourier-Bessel transform and time-frequency-based approach for detecting maneuvering air target in sea-clutter [J].,&, 2015, 9(5): 481-491. doi: 10.1049/iet-rsn.2014.0207.

[18] SURESH P, THAYAPARAN T, OBULESU T,. Extracting micro-Doppler radar signatures from rotating targets using Fourier-Bessel transform and time-frequency analysis[J]., 2014, 52(6): 3204-3210. doi: 10.1109/TGRS.2013. 2271706.

[19] SCHAUM S and ARFKEN G. Mathematical Methods for Physicists[M]. New York: Academic Press, 1970: 165-175.

[20] 胡晓伟, 童宁宁, 董会旭, 等. 弹道中段群目标平动补偿与分离方法[J]. 电子与信息学报, 2015, 37(2): 291-296. doi: 10.11999/JEIT140494.

HU Xiaowei, TONG Ningning, DONG Huixu,. Translation compensation and resolution of multi-ballistic targets in midcourse[J].&, 2015, 37(2): 291-296. doi: 10.11999/ JEIT140494.

[21] 张群, 罗迎. 雷达目标微多普勒效应[M]. 北京: 国防工业出版社, 2013: 22-30.

ZHANG Qun and LUO Ying. Micro-Doppler Effect of Radar Targets[M]. Beijing: National Defense Industry Press, 2013: 22-30.

张 群： 男，1964年生，教授，博士生导师，研究方向为雷达信号处理、雷达成像与目标识别.

何其芳： 女，1993年生，硕士生，研究方向为雷达信号处理.

罗 迎： 男，1984年生，副教授，博士生导师，研究方向为雷达成像与目标识别.

Micro-Doppler Feature Extraction of Group Targets Using Signal Decomposition Based on Bessel Function Basis

ZHANG Qun HE Qifang LUO Ying

(,,’710077,) (,’710077,)

Micro-Doppler (m-D) feature extraction is significant for group target discrimination, while the methods for single target are invalid. An m-D feature extraction method of group targets is proposed based on signal orthogonal decomposition. First, the Sinusoidal Frequency-Modulated (SFM) form of m-D signals and the decomposition result of the phase term on-resolution Bessel basis is deduced. The m-D frequency is coarsely estimated by the one-to-one relationship between frequencies and basis functions. Then an algorithm is introduced to reduce the error and thus a finer estimation is obtained. Finally, the m-D frequency of each target is extracted by discrete echoes without phase shift ambiguity. Simulation experiments validatethe effectiveness, and show that the proposed method outperforms the Sinusoidal Frequency Modulation Fourier Transform (SFMFT)-based method and Average Magnitude Difference Function (AMDF)-based method in estimation precision.

Micro-Doppler (m-D); Group targets; Bessel function basis; Feature extraction; Parameter estimation

TN957.51

A

1009-5896(2016)12-3056-07

10.11999/JEIT161036

2016-10-08；改回日期：2016-11-08；

2016-12-02

何其芳 qifanghe@163.com

国家自然科学基金(61471386, 61571457)

The National Natural Science Foundation of China (61471386, 61571457)