建立新型边缘泄露补偿机制的四阶方程图像平滑方法

易三莉，陈 勇，贺建峰

（昆明理工大学信息工程与自动化学院，云南昆明650500）

建立新型边缘泄露补偿机制的四阶方程图像平滑方法

易三莉，陈 勇，贺建峰

（昆明理工大学信息工程与自动化学院，云南昆明650500）

针对传统的四阶偏微分方程（四阶方程）降噪算法容易造成图像边缘泄露的问题，本文提出了一种基于边缘检测理论的泄露修补算法.该算法首先用非线性的双边滤波器对噪声图像进行预处理，得到边缘结构较好的预处理图像，然后基于梯度算子具有检测图像边缘特征的特点，提出将结果图像和预处理图像二者梯度差值的二范数平方作为边缘保持约束项，并将其加入到四阶方程算法的能量泛函中.另外，基于图像局部方差构造了自适应的拉格朗日乘子，从而实现对边缘保持约束项的自适应调整，以提高其边缘保持性能.实验测试结果表明，本文算法不仅继承了传统四阶算法具有的优点，而且增强了对边缘结构的保持能力.

四阶偏微分方程；边缘泄露；边缘检测；边缘保持约束

1 引言

数字图像在获取和传输过程中，均要受一定程度的噪声污染.受噪声污染的图像不仅影响其视觉效果，而且限制了其后续处理及分析利用，如图像分析及内容理解部分都需要较高质量的信号，因此图像的降噪复原成为了计算机底层视觉研究中的热点问题.

对图像进行降噪关键是要解决好去除噪声和保护边缘特征的这一对矛盾.目前，常用的图像降噪方法有：基于贝叶斯框架的统计模型［1］、小波方法［2］、稀疏表示方法［3］及基于偏微分方程的方法.其中，基于偏微分方程的方法因其具有简单有效、数学理论完备等技术优点而受到了广泛的重视.以Witkin等人［4］提出线性的各向同性扩散算法作为此类算法的开端，Perona等人［5［6］提出以高斯平滑后的梯度来代替扩散函数中的梯度计算；Black等人［7］提出了鲁棒各向异性扩散（RAD），该类算法指出了鲁棒统计学模型和各向异性扩散模型的联系；余庆军等人［8］以图像的局部方差作为屏蔽函数，提出了基于人类视觉系统的各向异性扩散方法；Gilboa等人［9］的复数域扩散算法，提出以复扩散函数代替实扩散函数，同时实现了高斯和拉普拉斯金字塔的多尺度分析；针对阶梯效应的问题，朱立新等人［10］提出在经典的二阶方程扩散算法中耦合了梯度保真项；王志明等人［11］依据像素点在其邻域内的灰度关系，提出对像素点进行分类平滑；Yang等人［12］依据中心像素点邻域内外区域之间的像素灰度相似性关系，提出了基于非邻域均值理论的P-M算法.值得特别注意的是，Yu等人［13］分析了经典二阶方程算法使结果图像存在阶梯效应的原因，并提出了四阶方程算法，该算法从理论上保证了所得结果图像为分段平面图像，并且该算法对高频噪声具有较强的平滑能力，但是该算法容易造成结果图像的边缘泄露而降低了其保护边缘特征的能力.针对四阶方程出现边缘泄露的问题，Li等人［14］提出将全变分算法和四阶方程算法相加权，并以此降低四阶方程部分在边缘等特征区域的平滑速度；Zhang等人［15］在四阶方程所对应的能量泛函中，将梯度算子和拉普拉斯算子相加权，以更好地测量图像的平滑性.以上算法虽然一定程度上改进了传统的四阶方程算法，但由于引入了全变分项，因此在平滑中带来了一定程度的阶梯效应，所以该问题仍值得更多地关注.

本文针对以上传统四阶方程算法在降噪过程中存在的问题，提出将边缘保持项作为其对应能量泛函的约束项，这样最小化能量泛函的过程就相当于平滑图像的同时使结果图像和原图像二者的边缘特征尽量保持一致；然后，基于对局部方差理论的分析，构造出具有自适应调整能力的拉格朗日乘子；最后，给出了本文模型的凸性证明.

2 传统四阶方程算法

用传统的二阶方程对图像进行降噪，容易使结果图像朝着分段常量图像演变.为了解决这一问题，Yu等人分析了问题的原因，并提出如下图像范围Ω内的能量泛函［13］：

式中，▽2为拉普拉斯算子，φ（·）≥0且φ（·）为单调增函数，即φ′（·）＞0.因此最小化式（1）就相当于平滑图像u，通过泛函极值处理，可以得到式（1）对应的欧拉-拉格朗日方程为：

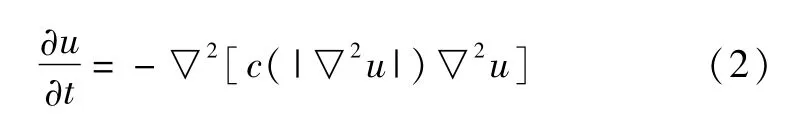
3 本文的四阶方程算法

3.1加入边缘保持约束项的四阶方程算法

针对上述四阶方程容易使结果图像产生边缘泄露的问题.本文根据梯度算子▽具有检测图像边缘特征的特点，提出将结果图像u和原始图像u（0）的梯度作差值，并将差值的二范数作为测量结果图像边缘和原始图像边缘差异的量度，然后将其二范数平方作为式（1）能量泛函的约束项.因此，加入边缘保持约束的能量泛函如下：

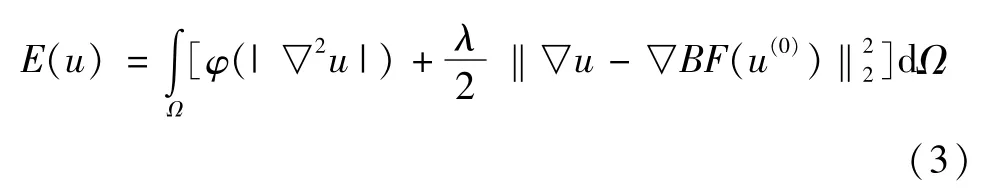
式中，λ（λ≥0）为拉格朗日乘子.BF（u（0））为原始图像u（0）经双边滤波器［17］预滤波的输出图像.双边滤波器的滤波过程如下：

式中，S是以p为中心像素点的邻域像素集，q为S中的像素点，σ为高斯核.‖p-q‖、|u（p）-u（q）|分别为像素点p到q的Euclidean空间距离测量和像素灰度相似性距离测量.由于双边滤波器具有简单及非线性等技术优点，因此该滤波器预处理的图像能较好的保持原始图像的边缘特征，克服了传统的高斯滤波器作为预处理滤波器易导致图像边缘模糊的不足.

因此，式（3）具有如下形式的欧拉-拉格朗日方程：

经过简单的导数计算，式（3）对应的欧拉-拉格朗日方程为：

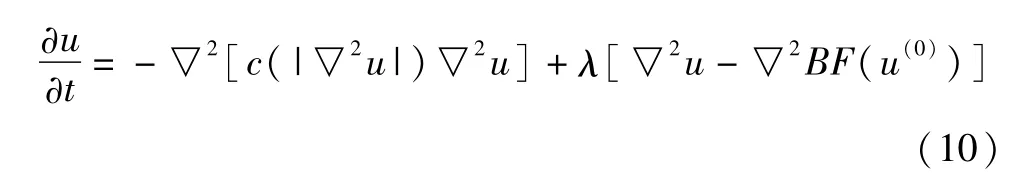
式中，拉格朗日乘子 λ起着平衡的作用，平衡平滑项（右边第一项）平滑图像和边缘保持约束项（右边第二项）阻止发生边缘泄露.

3.2拉格朗日乘子λ的自适应

式（10）中边缘保持项的拉格朗日乘子λ，应满足如下要求：自适应性，即能够根据图像的局部结构特征自适应地调整边缘保持项的权值；稳定性，即 λ值不应过大，以防止造成算法的不稳定性.

文献［18］认为，相较于梯度信息，图像的局部方差信息能更好地反映图像的局部结构特征，并且图像在边缘等异质区域的局部方差要大于同质区域的局部方差.图像的局部方差定义为：

式中，m（x，y）为像素点（x，y）在尺寸为（2N+1）×（2N +1）分析窗口内的局部均值.

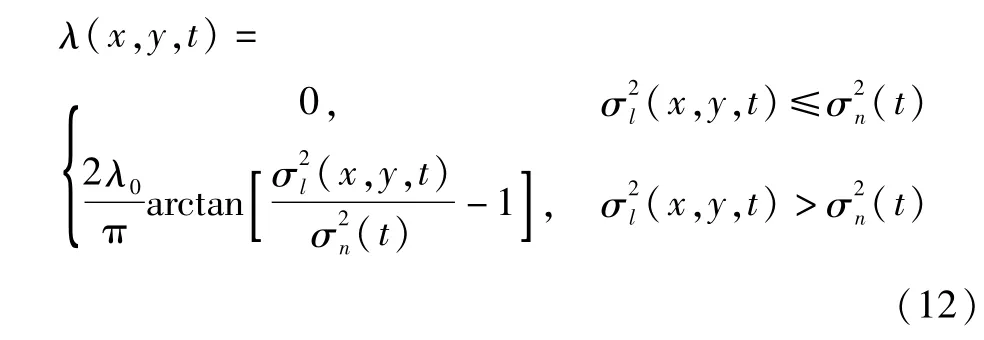
式中，λ0（λ0≥0）为可调参数.式（12）提出的λ自适应方案充分地利用了反正切函数的有界性质，即因此，合理地设置参数λ0，可以防止λ越界，进而保证算法式（10）的稳定性.

根据式（10）与式（12）我们可以看出拉格朗日乘子λ具有以下特点：

基于上述分析，我们可以看到，本文算法由于引入了自适应的拉格朗日乘子，使式（10）中的边缘保持项能够更好地发挥作用，从而使本文算法具有更好的自适应性和鲁棒性.

3.3本文模型凸性证明

对于边缘停止函数c（·），本文采用文献［8］中的方法进行定义：

式中，k（k＞0）为控制算法平滑范围的阈值.

对式（14）的φ′（s），求出其导数为：

然后，对任意常数a，b＞0（a+b=1），并对于图像u1、u2，由三角不等关系有：

由于φ（s）为单调递增函数，并结合式（16），有如下不等关系成立：

由式（15）知：φ″（s）＞0，即函数φ（s）是凸性的.结合式（17），故有如下不等关系成立：

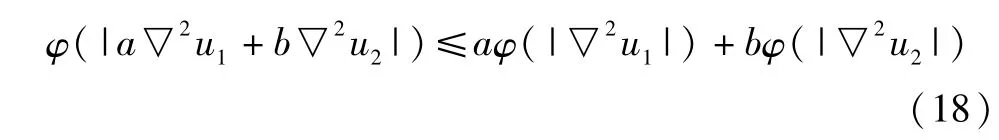
最后，又有如下不等关系：

式中，〈·〉表示向量内积运算.式（19）中，应用到了不等式：

由式（18）（19），并且λ≥0，有如下不等关系：

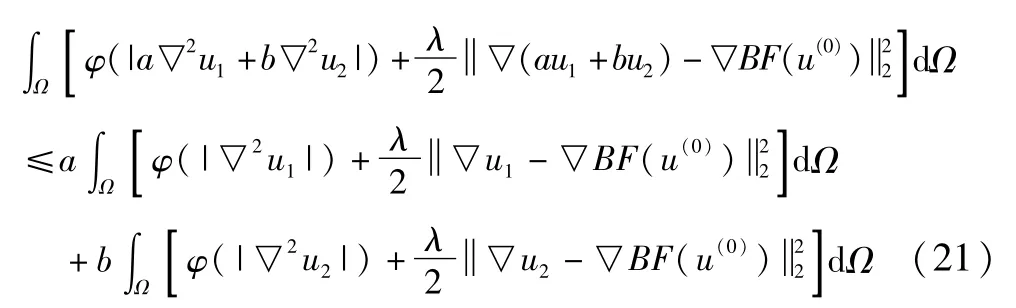
由不等关系式（21）知，本文能量泛函式（3）是凸性的，表明本文算法在加入边缘保持约束项后，唯一全局最优解的性质保持不变.

3.4数值实现及算法步骤

首先将本文算法式（10）数值化为：

式中，Δt为迭代的时间步长.

算法主要流程如下：

步骤1：确定参数 Δt、λ0、k、σd、σr、N和预滤波窗口S的大小，输入噪声图像u（0）；

步骤2：确定最大迭代次数nitermax.若迭代次数niter≤nitermax则进入步骤3；否则进入步骤4；

步骤4：退出迭代，以u（n+1）作为降噪后的结果图像.

4 实验结果及分析

针对本文算法的特点：既保留了传统四阶方程算法所具有的优点，又较好地解决了传统四阶方程算法易使结果图像出现边缘泄露的问题，增强了对图像边缘的保持能力，并且降低了图像质量对迭代次数（平滑时间）的敏感性.本文分别用不同类型的图像展开如下4部分实验，并用峰值信噪比（PSNR（dB））及平均结构相似度（MSSIM）［20］指标对前三部分的实验结果图像展开定量评价.其中，PSNR值越高，表明结果图像和原图像的差异越小；MSSIM∈［0，1］值越接近1，表明结果图像和原图像在亮度、对比度、结构相似度的信息上越接近.另外，在实验中将本文算法的参数取为：Δt=0.25、λ0=1、σd=1.5、σr=0.6、N=5、S=5，阈值参数 k根据不同图像的对比度进行合理选取，建议在k=0.5邻近选取.

相较于经典的二阶方程算法，为了验证本文算法和传统四阶方程算法的优势.本文将不同噪声水平（噪声方差）的高斯噪声叠加到Lena原图像中，并用本文算法及各个时期较为经典的算法：P-M算法、RAD扩散、复数域扩散及传统四阶方程方法对噪声图像进行降噪处理，所得结果如表1所示.为了便于从结果图像的视觉效果上说明各算法的特点，本文将情况下的实验结果展示在图1（c）～（h）中.

由图1（c）可见，λ（n=0）图像在一定程度上剔除了噪声的干扰，并反映出原图像的绝大部分特征信息.由图1 （d）～（h）中各算法降噪后的结果图像可以看到，P-M算法降噪后的结果图像如图1（d），可见图像中部分颗粒噪声并没有得到有效去除，且图像中存在阶梯效应；RAD扩散降噪后的结果图像如图1（e），可见该算法与P-M算法类似，仍难以消除颗粒噪声的干扰；复数域扩散降噪后的结果图像如图1（f），图像受所谓的“棋盘”效应的影响，在去除颗粒噪声方面与前面两种算法类似；传统四阶方程算法迭代14次后（为了说明问题，进行14次迭代）的结果图像如图1（g），图像各部分区域较为平滑而不受阶梯效应的影响，但图像出现了边缘泄露的问题，造成结果图像的边缘较为模糊；本文算法迭代14次后的结果图像如图1（h），可见本文算法的降噪效果较为明显，图像中各部分区域也较为平滑，但和使用相同迭代次数的传统四阶方程算法不同的是，本文算法由于边缘保持项发挥了作用，因而使结果图像的边缘等特征信息较为清晰，一定程度上遏制了边缘泄露现象的发生.

表1　各算法的评价指标值

为了验证3.2节所述的拉格朗日乘子自适应方案的特点，将本文算法与上述实验对比算法作迭代实验的比较.首先将方差为0.015的高斯噪声叠加到Peppers原图像中，然后分别用本文算法和对比算法对所得到的噪声图像展开25组迭代实验（2次迭代～50次迭代，步长为2次），并根据MSSIM指标的特点，用MSSIM指标定量评价各次迭代的结果图像，所有结果图像的MSSIM评价值如图2所示.其中，传统四阶方程算法及本文算法在 n=8，16，24，32，40及48次迭代时的结果图像分别展示于图3～4中.

从图2可以看到，本文算法在2次迭代时的MSSIM值低于传统四阶方程算法，但随着迭代次数的增加，本文算法的MSSIM值都要显著高于传统四阶方程算法及其它对比算法，并且这种趋势越来越明显.这些都表明，由于本文算法的边缘保持项及拉格朗日自适应方案的作用，一定程度上克服了传统四阶方程算法使结果图像出现边缘泄露而模糊边缘的问题，并且降低了结果图像的质量对迭代次数增加的敏感性.另外，根据图3～4中的结果图像，可以从视觉效果上确认本文算法的这一特点.

相较于文献［14，15］所改进的四阶方程算法，为了验证本文算法的优势，本文将不同噪声水平的高斯噪声叠加到Goldhill原图像中，并用本文算法和文献［14，15］中的算法对噪声图像进行降噪处理，所得结果如表2所示.并将情况下的实验结果展示在图5（a）～（e）中.

由图5（c）～（e）中各算法降噪后的结果图像可以看到，文献［14］算法降噪后的结果图像如图5（c）和文献［15］算法降噪后的结果图像如图5（d），两图像均受一定程度的阶梯效应的影响，这是由于该两种算法都在传统四阶方程算法中引入了全变分项，并以此防止边缘泄露的发生，但由于全变分项的作用，使图像局部朝着分段常量图像演变，进而产生阶梯效应.本文算法降噪后的结果图像如图5（e），如前述，取得较好的降噪效果.另外，从各噪声水平下的降噪情况来看，表2中的数据说明本文算法在 PSNR和MSSIM评价值上要优越于另外两种算法.

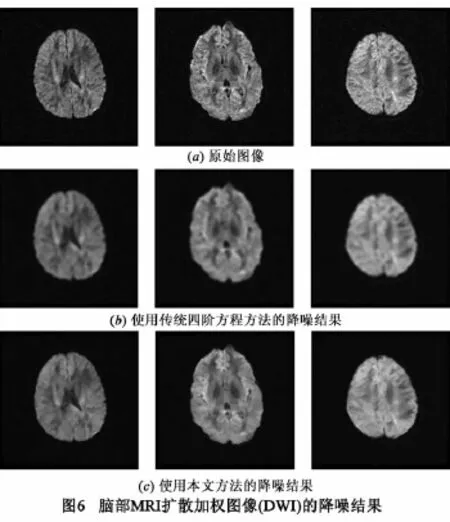
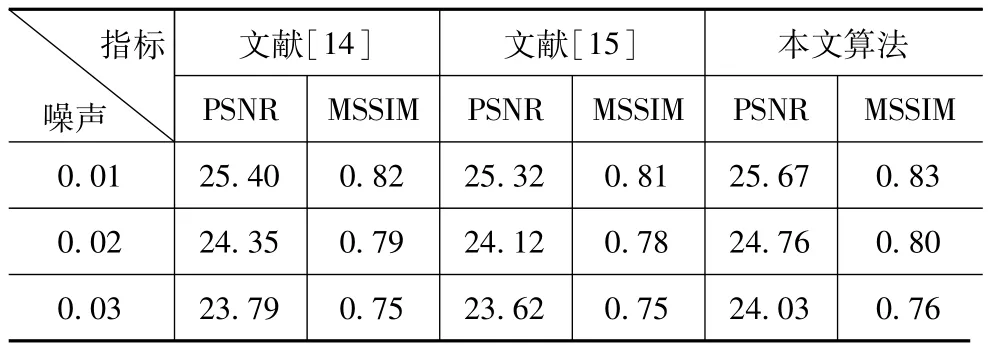
表2　各算法的评价指标值

上文实验均为对人为合成的噪声图像进行的实验，为了验证本文算法对真实噪声图像进行降噪的有效性.本文选用3幅不同层面的含Rician噪声的脑部MRI扩散加权图像（DWI）进行测试.3幅原图像如图6 （a）所示，使用传统四阶方程方法降噪后的结果图像如图6（b）所示，本文算法降噪后的结果图像如图6（c）所示.

相较于图6（b）中使用传统四阶方程方法得到的结果图像（均迭代8次），由图6（c）中本文算法的结果图像（均迭代14次）可见，图像在背景区域内较为平滑，信号区域的边缘、纹理信息保持的较为完好和清晰.因此，表明了本文算法对真实噪声图像进行降噪的有效性和实用性.

5 结论

通过对传统四阶方程算法添加边缘保持约束，较好地解决了传统四阶方程算法容易使结果图像出现边缘泄露的问题，增强了对边缘的保持能力，并降低了图像质量对迭代次数增加的敏感性.通过展开一系列实验，其结果验证了本文算法的有效性和实用性.为了进一步增强本文算法的边缘保持能力，下一步研究的重点将是如何改进边缘保持约束项中边缘检测算子的鲁棒性，以更精确地从噪声图像中获取其边缘信息.另外，还可以将本文算法的边缘保持约束项推广应用到其它四阶方程算法［21，22］，以获得更好的效果.

［1］李春芳，杨鑫，张旭明，丁明跃.基于MAP的超声图像分解去噪算法研究［J］.电子学报，2014，42（7）：1291 -1298. Li Chun-fang，Yang Xin，Zhang Xun-ming，Ding Mingyue.MAP based ultrasound image decomposition and denoising method［J］.Acta Electronica Sinica，2014，42（7）：1291-1298.（in Chinese）

［2］徐小军，王友仁.基于离散分数阶正交小波变换图像降噪新方法［J］.电子学报，2014，42（2）：280-287. Xu Xiao-jun，Wang You-ren.Novel image denoising method based on discrete fractional orthogonal wavelet transform［J］.Acta Electronica Sinica，2014，42（2）：280-287. （in Chinese）

［3］徐焕宇，孙权森，李大禹，宣丽.基于投影的稀疏表示与非局部正则化图像复原方法［J］.电子学报，2014，42 （7）：1299-1304. Xu Huan-yu，Sun Quan-sen，Li Da-yu，Xuan Li.Projectionbased image restoration via sparse representation and nonlocal regularization［J］.Acta Electronica Sinica，2014，42 （7）：1299-1304.（in Chinese）

［4］Witkin A P.Scale space filtering［A］.Proceedings of International Joint Conference on Artificial Intelligence［C］. New York，USA：Artificial Intelligence，1983.1019-1021. ［5］Perona P，Mailik J.Scale space and edge detection using anisotropic diffusion［J］.IEEE Transactions on Pattern A-nalysis and Machine Intelligence，1990，12（7）：629-639. ［6］Catte F，Lions P L，Morel J M，Coll T.Image selective smoothing and edge detection by nonlinear diffusion［J］. SIAM Journal on Numerical Analysis，1992，29（1）：182 -193.

［7］Black M J，Sapiro G，Marimont D H，Heeger D.Robust anisotropic diffusion［J］.IEEE Transactions on Image Processing，1998，7（3）：421-432.

［8］余庆军，谢胜利.基于人类视觉系统的各向异性扩散图像平滑方法［J］.电子学报，2004，32（1）：17-20. Yu Qing-jun，Xie Sheng-li.An anisotropic diffusion image smoothing method based on human visual system［J］.Acta Electronica Sinica，2004，32（1）：17-20.（in Chinese）

［9］Gilboa G，Sochen N，Zeevi Y Y.Image enhancement and denoising by complex diffusion process［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2004，26（8）：689-703.

［10］朱立新，王平安，夏德深.引入耦合梯度保真项的非线性扩散图像去噪方法［J］.计算机研究与发展，2007，44 （8）：1390-1398. Zhu Li-xin，Pheng Ann Heng，Xia De-shen.Nonlinear diffusion based image denoising coupling gradient fidelity term［J］.Journal of Computer Research and Development，2007，44（8）：1390-1398.（in Chinese）

［11］王志明，张丽.局部结构自适应的图像扩散［J］.自动化学报，2009，35（3）：244-250. Wang Zhi-ming，Zhang Li.Local-structure-adapted image diffusion［J］.Acta Automatica Sinica，2009，35（3）：244 -250.（in Chinese）

［12］Yang M，Liang J K，Zhang J H，et al.Non-local means theory based Perona-Malik model for image denoising ［J］.Neurocomputing，2013，120（SI）：262-267.

［13］You Y，Kaveh M.Fourth-order partial differential equations for noise removal［J］.IEEE Transactions on Image Processing，2000，9（10）：1723-1730.

［14］Li F，Shen C M，Fan J S，Shen C L.Image restoration combining a total variational filter and a fourth-order filter ［J］.Journal Visual Communication&Image Representation，2007，18（4）：322-330.

［15］Zhang J H，Li L C，Yang J.An enhanced fourth-order PDE model based on laplacian and gradient operator［A］. Proceedings of International Conference on Computer and Information Technology［C］.Nanjing，China：IEEE，2012.144-146.

［16］Gonzalez R C，Woods R E.数字图像处理［M］.阮秋琦，阮宇智，译.北京：电子工业出版社，2010.

［17］Danny Barash.A fundamental relationship between bilateral filtering，adaptive smoothing，and the nonlinear diffusion equation［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2002，24（6）：844-847.

［18］Chao S M，Tsai D M.An improved anisotropic diffusion model for detail and edge preserving smoothing［J］.Pattern Recognition Letters，2010，31（13）：2012-2023.

［19］Jing T，Li C.Image noise estimation using a variation adaptive evolutionary approach［J］.IEEE Signal Processing Letters，2012，19（7）：395-398.

［20］Wang Z，Bovik A C，Sheikh H R，Simoncelli E P.Image quality assessment：from error visibility to structural similari-ty［J］.IEEE Transactions on Image Processing，2004，13（4）：600-612.

［21］Lysaker M，Lundervold A，Xue-Cheng T.Noise removal using fourth order partial differential equation with applications to medical magnetic resonance images in space and time［J］.IEEE Transactions on Image Processing，2003，12（12）：1579-1590.

［22］贾迪野，黄凤岗，苏菡.一种新的基于高阶非线性扩散的图像平滑方法［J］.计算机学报，2005，28（5）：882 -891. Jia Di-ye，Huang Feng-gang，Su Han.A new noise removal method based on fourth order nonlinear diffusion［J］. Chinese Journal of Computer，2005，28（5）：882-891.（in Chinese）

易三莉 女，1977年12月出生，湖南岳阳人.2011年毕业于中南大学生物医学工程系，取得博士学位，2012年进入昆明理工大学生物医学工程系从事医学图像处理方面的研究.

E-mail：152514845@qq.com

贺建峰（通信作者） 男，1965年7月出生，云南开远人.教授，主要研究方向为医学影像与模式识别.

E-mail：jfenghe@qq.com

陈 勇 男，1986年11月出生，四川泸县人.硕士研究生.主要研究方向为计算机图像处理与模式识别.

E-mail：2269134036@qq.com

A Novel Compensation Mechanism of Edge Leakage for Fourth Order Equation Smoothing Image

YI San-li，CHEN Yong，HE Jian-feng

（Faculty of Information Engineering and Automation，Kunming University of Science and Technology，Kunming，Yunnan 650500，China）

As the traditional fourth order partial differential equation（fourth order equation）algorithm causes edge leakage of image，a leakage compensation method is proposed based on edge detection theory.Firstly the noise image is preprocessed by a nonlinear bilateral filter to obtain the better edge preservation image.Based on the feature of the gradient operator on the detection of image edge and the squared two-norm of gradient difference which is between the result image and the preprocessed image，a constraint item is built.Then the constraint item is added to the corresponding energy functional of fourth order equation.Finally，to adaptively adjust the edge preservation constraint item and improve the performance of edge preservation，an adaptive Lagrange multiplier which is based on image local variance is constructed.The experimental results show that the proposed algorithm not only inherits the advantage of traditional fourth order equation，but also enhances its ability of edge preservation.

fourth order partial differential equation；edge leakage；edge detection；edge preservation constraint

TP391.41

A

0372-2112（2016）04-0813-08

电子学报URL：http：//www.ejournal.org.cn 10.3969/j.issn.0372-2112.2016.04.009

2014-10-21；

2015-01-20；责任编辑：孙瑶

国家自然科学基金（No.11265007）；教育部回国人员科研启动基金（No.2010-1561）；云南省人培基金（No.KKSY201203030）