一种广义主成分提取算法及其收敛性分析

2016-10-13高迎彬孔祥玉胡昌华张会会侯立安

电子与信息学报 2016年10期

高迎彬孔祥玉胡昌华张会会侯立安

一种广义主成分提取算法及其收敛性分析

高迎彬孔祥玉*胡昌华张会会侯立安

(第二炮兵工程大学西安 710025)

广义主成分分析在现代信号处理的诸多领域发挥着重要的作用。目前，自适应广义主成分分析算法还并不多见。针对这一现状，该文提出一种快速收敛的广义主成分分析算法，并通过理论分析所提算法的确定性离散时间系统，导出了保证算法收敛的学习因子和初始权向量模值等边界条件。仿真实验和实际应用验证了所提算法的正确性和有用性。仿真结果还表明，所提算法比现有同类算法具有更快的收敛速度和更高的估计精度。

广义主成分；确定性离散时间；收敛性分析；神经网络

1 引言

广义主成分分析是现代信号处理和数据分析领域内的一门重要工具，已经广泛应用于如雷达信号处理[1]，移动通信[2]，盲信号分离[3]，医学检查[4]等各个领域。因此发展广义主成分分析算法是非常有意义的工作。

为了求解上述问题，一些学者提出了数值算法[5]。然而这些算法均是批处理算法，计算复杂度非常大，而且这些算法还要求输入信号的自相关矩阵是已知的，而在实时信号处理领域输入信号的自相关矩阵通常是不确定的，只能根据输入信号来进行在线估计，因此这些数值算法是难以满足实时信号处理的需要。近些年来，学者们相继提出了一些采用神经网络来进行广义主成分提取。相比传统的数值算法，神经网络算法具有以下3个方面的优点：(1)可以对输入信号的自相关矩阵进行在线估计；(2)算法的计算复杂度较低；(3)能够处理非平稳的随机信号[9]。因此基于神经网络的广义主成分分析算法研究成为了近些年来国内外一个研究热点。本文提出了一种新的广义主成分分析算法。相比一些现存算法，该算法具有算法形式简单、收敛速度快、收敛精度高等特点。

神经网络算法的收敛性分析是一个非常值得研究的问题。通过对其进行收敛性分析，给出神经网络算法收敛的边界条件，这对于神经网络算法的实际应用十分有利。一般而言，神经网络算法是由其对应的随机离散时间(Stochastic Discrete Time, SDT)来描述的，这就使得直接对神经网络算法进行分析变得十分困难[10]。长期以来，学者们相继提出了一些间接分析方法，主要有：确定性连续时间(Deterministic Continuous Time, DCT)方法和确定性离散时间(Deterministic Discrete Time, DDT)方法。相比DCT方法，DDT方法可以保留神经网络算法的离散本质[11]，而且可以允许神经网络算法的学习因子为一个常值，十分符合实际使用的需要，因此成为近些年来人们研究的一个热点。近些年来，学者们相继采用DDT方法对一些神经网络算法进行了收敛性分析，取得了很多成果。然而以上所提文献中的所有算法都针对的是一般主成分分析问题，到目前为止，还很少有文献对广义主成分分析算法采用DDT方法进行研究。由于相比一般主成分分析算法，广义主成分分析算法形式复杂，所以采用DDT方法对广义主成分分析算法进行分析时也会比一般主成分分析算法复杂。因此采用DDT方法对广义主成分分析算法进行收敛性分析就显得很有必要。因此本文将采用DDT方法对所提广义主成分分析算法进行收敛性分析，确定其收敛的边界条件。

本文的结构安排如下：在第2节中，提出了一种新的广义主成分分析算法；在第3节中采用DDT方法对所提算法进行收敛性分析，确定了所提算法的收敛性条件；第4节主要是通过两组仿真实验对所提算法的性能进行验证；本文的总结结论安排在第5节。

2 一种广义主成分分析算法

目前，基于Hebb神经网络的广义主成分分析算法的研究是国际上的一个研究热点。Hebb是一个具有线性形式的神经网络，它在迭代过程中不引入后项传播误差来更新权矩阵，其权值更新只依靠相应神经元的输入输出乘积。Hebb神经网络的神经元模型可以通过式(2)来描述：

近些年来，基于Hebb神经网络学者们提出了一些的广义主成分分析算法。这些方法按照提出方式可以分为两类：一类是基于某种信息准则导出的算法，如RLS算法[6]；另一类是基于某种启发式推理而提出的，如R-GEVE算法[13]等。虽然第2类算法缺乏相对应的信息准则，但是这并没有限制算法的使用，也不会影响对算法进行收敛性分析。本文提出了一个基于启发式推理的神经网络权向量更新算法：

表1自适应广义主成分分析算法

3 算法的收敛性分析

本节采用DDT方法对所提算法进行收敛性分析：对式(6)施加条件期望因子，并将辨识的条件期望值作为下一次迭代值，则可获得所提算法的DDT系统[10]，该系统与式(3)形式相同。

接下来，通过定理1-定理6来完成对所提算法进行收敛特性分析。

证明应用式(3)，可以得到

将式(8)代入式(10)可得

定理1主要完成的是权向量模值的上限证明，定理2则提供了权向量模值下限的分析。

证明根据式(8)，可得

通过定理1和定理2可以完成式(3)的边界性证明。下面，将证明在一些温和的条件下，式(3)中权向量将最终收敛到矩阵束的广义主成分。为了分析式(3)的收敛性，这里通过定理3给出一些预备结论。

证毕

证明由式(24)和定理4，定理5可得

证毕

到此就完成了对所提算法的收敛性证明。下面对所提算法收敛性条件进行讨论。从条件和可得，所提算法学习因子的选择与最大广义特征值有关。在实际应用过程中，尽管最大广义特征值是未知的，但是它的上限是可以被估计得出的[12]。因此，学习因子的限制条件是可以达到的。此外，当初始权向量为随机产生时，初始权向量的条件是以概率1满足的。因此可以说，通过DDT分析获得的所提算法的收敛性条件是符合实际使用需要的。

4 仿真实验

本节将提供两个实验是对所提算法的性能验证。第1个实验是考验算法对于两个随机输入向量的广义特征向量提取的能力以及和其他算法的性能比较；第2个实验是应用所提算法解决盲信号分离问题。

4.1广义主成分提取实验

本实验目的是对所提算法的广义主成分提取能力进行实验验证。这里将所提算法与RLS算法[6]和FPI-GED算法[7]进行对比。为了能够衡量所提算法的性能，这里引入方向余弦作为评价函数：

在仿真实验过程中，神经网络的输入向量由式(38)和式(39)产生[6]：

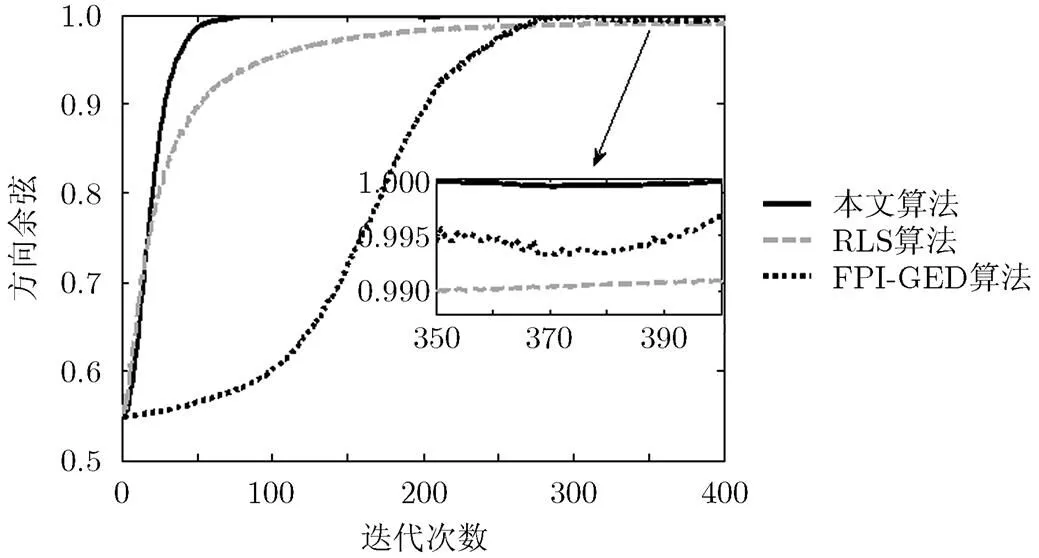
图1 两种算法的方向余弦曲线

从图1中可以看出：相比RLS算法和FPI-GED算法，本文所提算法具有较快的收敛速率。此外，虽然两种算法的方向余弦最终均收敛到了1附近，但是当把仿真的最后50步进行放大后可以发现：本文所提算法与单位1的接近程度要优于RLS算法。由于方向余弦可以表征算法的收敛精度，所以可以得出结论：相比RLS算法和FPI-GED算法，本文所提算法不仅具有较快的收敛速度而且具有较高的收敛精度。

4.2盲信号分离实验

本实验主要是应用所提算法解决盲信号分离问题。考虑式(40)所示的盲分离模型：

在本实验将ICALAB中的ABio7.mat(获取地址为：http://www.bsp.brain.riken.go.jp/ICALAB/)中的4个信号作为输入，如图2所示，图中横纵坐标为时刻，纵坐标为幅值。盲信号的混合矩阵为

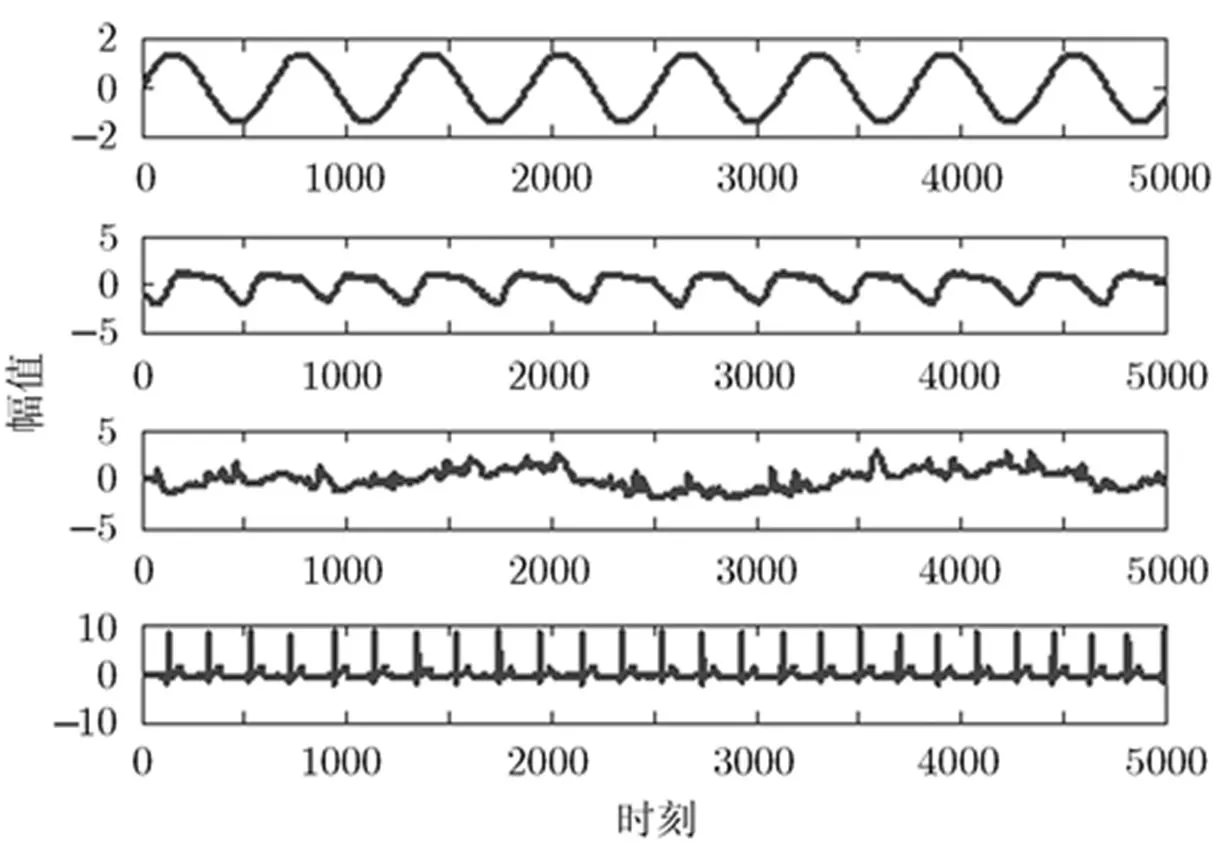
图3分离信号曲线

表2原信号和分离信号的互相关系数

从图3和表2中可以看出，采用本文所提算法获得的分离信号与源信号之间具有很强的相似性。虽然本文算法的分离结果略逊于广义特征值分解算法，但是本文算法是可以在线进行的，而广义特征值分解算法是一种批处理算法，而且具有很高的计算复杂度。

5 结论

本文提出了一种新型的广义主成分分析算法，并采用一种DDT分析方法对所提算法进行了收敛性分析，确定了保持该算法收敛性的边界条件，为算法的实际应用奠定了基础。仿真实验和实际应用表明：相比一些现有广义主成分分析算法，本文所提算法不仅具有很快的收敛速度而且具有很高的估计精度。

参考文献

[1] 谢荣, 刘峥, 刘俊. 基于矩阵束的MIMO雷达低仰角快速估计方法[J]. 电子与信息学报, 2011, 33(8): 1833-1838. doi: 10.3724/SP.J.1146.2010.01242.

XIE Rong, LIU Zheng, and LIU Jun. Fast algorithm for low elevation estimation based on matrix pencil in MIMO radar[J].&, 2011, 33(8): 1833-1838. doi: 10.3724/SP.J.1146.2010.01242.

[2] 蔡振浩, 赵昆, 陈文. TD-LTE-A 系统下行多用户CoMP 联合预编码算法[J]. 北京邮电大学学报, 2015, 38(1): 67-70.

CAI Zhenhao, ZHAO Kun, and CHEN Wen. Research on CoMP joint transmission for downlink MU-MIMO in TD-LTE-A[J]., 2015, 38(1): 67-70.

[3] ANA Maria Tomé. The generalized eigen-decomposition approach to the blind source separation problem[J]., 2006, 16: 288-302.

[4] ZHANG Weitao, LOU Shuntian, and FENG Dazheng. Adaptive quasi-newton algorithm for source extraction via CCA approach[J]., 2014, 25(4): 677-689.

[5] WANG Shougen and ZHAO Shuqin. An algorithm for=with symmetric and positive-definiteand[J]., 1991, 12(4): 654-660.

[6] YANG Jian, XI Hongsheng, and YANG Feng. RLS-based adaptive algorithms for generalized eigen-decomposition[J]., 2006, 54(4): 1177-1188.

[7] YANG Jian, HU Han, and XI Hongsheng. Weighted

non-linear criterion-based adaptive generalised eigen

decomposition[J]., 2013, 7(4): 285-295.

[8] Tuan Duong Nguyen and Isao Yamada. Adaptive normalized quasi-Newton algorithms for extraction of generalized eigen-pairs and their convergence analysis[J]., 2013, 61(6): 1404-1418.

[9] MÖLLER R. A self-stabilizing learning rule for minor component analysis[J]., 2004, 14(1): 1-8.

[10] ZUFIRIA P J. On the discrete-time dynamics of the basic Hebbian neural-network node[J]., 2002, 13(6): 1342-1352.

[11] GAO Yingbin, KONG Xiangyu, HU Changhua,. Convergence analysis of möller algorithm for estimating minor component[J]., 2015, 42(2): 355-368.

[12] Tuan Duong Nguyen and IsaoYamada. Necessary and sufficient conditions for convergence of the DDT systems of the normalized PAST algorithms[J]., 2014, 94: 288-299.

[13] ATTALLAH S and ABED-MERAIM K. A fast adaptive algorithm for the generalized symmetric eigenvalue problem[J]., 2008, 15: 797-800.

A Generalized Principal Component Extraction Algorithm and Its Convergence Analysis

GAO Yingbin KONG Xiangyu HU Changhua ZHANG Huihui HOU Li’an

(,’710025,)

The generalized principal component analysis plays an important roles in many fields of modern signal processing. However, up to now, there are few algorithms, which can extract the generalized principal component adaptively. In this paper, a generalized principal component extraction algorithm, which has fast convergence speed, is proposed. The corresponding Deterministic Discrete Time (DDT) system of the proposed algorithm is analyzed and some conditions about the learning rate and initial weight vector are also obtained. Finally, computer simulation and practical application results show that compared with some existing algorithms, the proposed algorithm has faster convergence speed and higher estimation accuracy.

Generalized principal component; Deterministic Discrete Time (DDT); Convergence analysis; Neural networks

TP391

1009-5896(2016)10-2531-07

10.11999/JEIT151433

2015-12-17；改回日期：2016-05-10；网络出版：2016-07-04

孔祥玉 xiangyukong01@163.com

国家自然科学基金面上项目(61074072, 61374120)，国家杰出青年基金(61025014)

The National Natural Science Foundation of China (61074072, 61374120), The National Science Fund for Distinguished Youth Scholars (61025014)

高迎彬：男，1986年生，博士生，研究方向为自适应信号处理.

孔祥玉：男，1967年生，教授、博士生导师，研究方向为自适应信号处理、非线性系统建模和故障诊断.

胡昌华：男，1966年生，教授、博士生导师，研究方向为导弹测试与故障诊断.

张会会：男，1986年生，博士生，研究方向为故障诊断与寿命预测.