基于不确定集的稳健MIMO雷达波形设计算法

李秀友 薛永华 黄 勇 关 键



基于不确定集的稳健MIMO雷达波形设计算法

李秀友*薛永华 黄 勇 关 键

(海军航空工程学院信息融合技术研究所 烟台 264001)

针对雷达目标回波信号存在不确定性导致MIMO雷达波形优化设计性能下降问题，该文提出一种扁平椭球不确定集约束下的稳健自适应发射-接收波形联合优化设计方法。首先将目标脉冲响应的误差推广到更为一般的扁平椭球不确定集约束条件，并利用Lagrange乘子法对优化过程进行推导，得出扁平椭球不确定集约束下的闭式表达式。其次为了提高目标脉冲响应不确定集范围较大时的优化性能，采用了迭代鲁棒最小方差法进行求解(IRMVB)，求得更为精确的目标脉冲响应，提高了SINR改善性能。然后进一步分析了基于扁平椭球不确定集约束条件与球体约束条件优化问题的内在联系，推导得出该文求解过程为广义对角加载方法。最后通过仿真实验表明所提算法对于目标回波信号不确定性具有更高的稳健性。

MIMO雷达；波形设计；扁平椭球；Lagrange函数

1 引言

大量文献研究了基于目标检测的波形优化设计方法，以最大化目标信号输出SINR为准则，基于已知的目标脉冲响应时域或频域表示式，提出宽带雷达发射-接收波形联合优化设计方法。波形设计中通常假设目标脉冲响应是先验已知的确定量或服从给定统计特性的随机变量，但实际雷达目标回波同时具有方位敏感性、幅度起伏性和初相随机性等特点[6]。这些因素导致雷达目标回波信号具有较大的不确定性，给波形优化设计带来较大的难度，也会明显降低所设计优化波形的性能。文献[7,8]研究了基于国家土地覆盖数据库(NLCD)等辅助知识的波形设计方法，但是杂波强度与雷达系统参数及工作模式有关，并且杂波存在起伏现象，很难得到指定距离-方位分辨单元内精确的杂波RCS值。文献[9,10]提出了基于反馈结构的认知雷达工作流程图，通过场景分析器得到环境模型参数。文献[11]首先利用常规脉冲串估计场景参数，再根据估计值设计自适应波形使得目标SCNR最大化，这种基于实测回波数据估计的方法存在一定的估计误差。当杂波统计特性先验已知时，通常将杂波(噪声)建模为给定协方差矩阵的统计模型，再根据给定的杂波和噪声优化发射波形，其中杂波模型的精确程度将直接影响波形优化设计性能[12]及杂波抑制能力[13]。

在大量自适应波束形成算法中，为了提高算法在误差情况下的稳健性，相继提出了基于期望信号导向矢量不确定集约束下的稳健算法，导向矢量约束于各种不确定集合中，包括球体不确定集[14]、椭球体不确定集、扁平椭球不确定集[15]等，确保了导向矢量误差在一定范围内变化时，波束形成器仍能满足性能要求。文献[16]针对期望导向矢量不确定集较大时自适应波束形成输出SINR损失较大的问题，提出了迭代鲁棒最小方差算法(IRMVB)，采用较小的不确定集迭代求解，逼近更为准确的期望导向矢量。

文献[17]根据阵列流形测量值的变化范围确定不确定集大小，当不确定集各向异性时，可以用扁平椭球不确定集建模阵列流形变化特性。又由文献[18]关于目标1维距离像分析可知，目标1维距离像(目标脉冲响应)强度起伏的均值和方差各不相同，即目标脉冲响应存在于各向异性的不确定集中，因此可以将目标脉冲响应建模为更为精确的扁平椭球不确定集，其中强度均值对应椭球中心，强度方差对应椭球半径，相比于球体不确定集，用椭球不确定集模型建模各向异性的不确定集，不会导致不确定集范围的增大。文献[19]研究了MIMO雷达目标脉冲响应在球体误差约束条件下发射波形和接收波形的联合优化设计方法，提出了一种新的迭代优化算法，保证在误差范围内最差条件下的最优波形设计。但是该文献仅考虑了目标脉冲响应误差范围约束于一个球体的特殊情况，没有考虑更为一般的椭球体和扁平椭球体等不确定集约束条件，也没有考虑当不确定集较大时SINR改善性能下降的问题[20]。

针对以上分析的问题，本文在MIMO雷达联合发射-接收波形优化设计过程中，首先将目标脉冲响应的误差推广到更为一般的扁平椭球不确定集约束条件，并利用Lagrange乘子法对优化过程进行推导，得出扁平椭球不确定集约束下的闭式表达式；其次为了提高目标脉冲响应不确定集范围较大时的优化性能，采用了迭代鲁棒最小方差法进行求解，求得更为精确的目标脉冲响应，提高了SINR性能；然后进一步分析了基于扁平椭球不确定集约束条件与球体约束条件优化问题的内在联系，推导得出本文求解过程为广义对角加载方法；最后通过仿真结果比较分析本文算法的有效性。

2 稳健的发射波形和接收波形联合设计方法

当目标雷达信号脉冲响应、杂波脉冲响应和噪声二阶统计量已知时，波形设计的目的是设计维发射信号矢量和维接收波形矢量使得检测概率最大化，最优检测器可以由对数似然比检验得到，且检测概率是SINR的单调递增函数，因此，波形设计的目标等价于通过选取和使得SINR最大化。

2.1 问题描述

图1 系统工作模型图

其中L是有限持续信号的阶数，定义接收信号

其中L是接受滤波器的阶数，整体接收信号可以表示为

其中

和

其中扁平椭球不确定集约束表示为

2.2迭代求解算法

根据文献[19]的分部迭代算法，问题1具体迭代步骤如下，其中步骤1用于初始化，步骤8计算相邻两次SINR的改善值，当改善值足够小时循环结束。算法具体步骤如下(记为算法1)：

步骤6 求取

3 不确定集约束下的目标冲激响应优化求解

上述算法1迭代过程中的步骤3和步骤6在不同约束条件下有着不同的求解表示式。文献[19]推导了目标脉冲响应在球体不确定集约束下的求解表达式，但没有考虑误差更一般的扁平椭球不确定集约束条件下的解析表达式，本文将误差集合定义为更一般的扁平椭球不确定集，并通过推导得到解析表达式，将复杂的不确定集优化问题转化为Lagrange乘子的线性搜索问题，针对不确定集范围较大时，SINR改善性能下降的问题，采用了迭代鲁棒最小方差法进行迭代逼近，进一步提高优化波形对SINR的改善性能。

3.1不确定集约束下问题求解

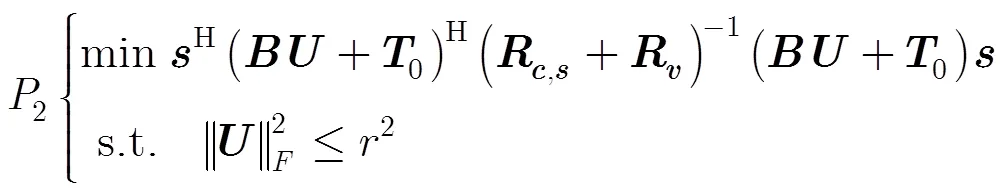
对问题2的目标函数进行分解，得到表示式

令

和

由于式(13)右侧第4项为确定值，优化过程中可以省略，并将式(14)和式(15)代入式(13)进行变量替换，则优化问题2可以写成

为了求解式(16)，构造Lagrange函数将约束优化模型转化为无约束优化问题。

则式(19)可以写成

则可求得

代入式(11)则可得到

利用相同的处理方法可以求解算法1步骤6的问题，表示式为

Egger′s检验(t=0.39，P=0.708)、Begg′s检验(Z=-0.27，P=0.784)和漏斗图(图5)的结果均提示，本篇Meta分析不存在发表偏倚。

3.2迭代鲁棒最小方差法

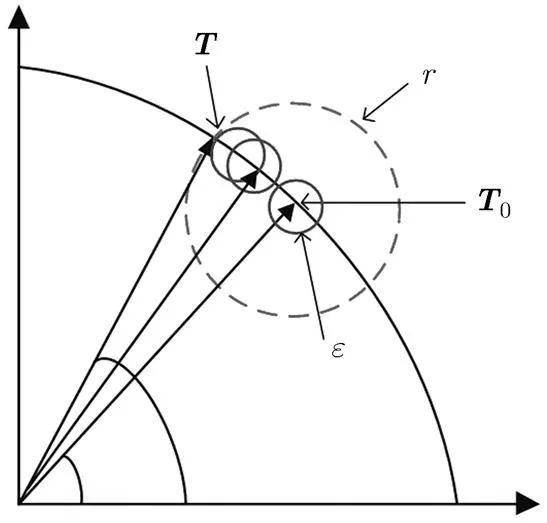
图2 IRMVB算法示意图(虚线大圆表示原始不确定集r，实线小圆表示用于迭代搜索的小不确定集)

迭代鲁棒最小方差法具体步骤如下(记为算法2)：

3.3算法分析

综上所述，算法1迭代过程中的步骤3和步骤6需要调用算法2求解，利用迭代鲁棒最小方差法缩小不确定集范围，进一步降低目标失配损失。算法2的步骤2利用式(23)将复杂的不确定集优化问题转化为Lagrange乘子的线性搜索问题，大大降低了运算量。

4 仿真结果及性能分析

在仿真实验中，为了便于对比分析，参数设置与文献[19]保持一致。假设MIMO雷达系统发射天线数，接收天线数，目标脉冲响应阶数为16阶，的系数为独立同分布复高斯随机变量。杂波脉冲响应建模为AR过程，协方差表达式为

图3 矩阵AR过程中使用的参数

实验1 目标存在于椭球不确定集时不同算法的收敛特性 从图4可以看出，对于确定已知目标，算法具有单调性，保证了较快的收敛速度。对于不确定目标，由于每步迭代过程中要在不确定集中搜索最差情况的目标脉冲响应，因此没法保证单调性，但局部非单调起伏不影响整体收敛趋势，随着迭代次数的增加均能趋于收敛。图4给出了一次迭代过程收敛曲线，当存在扁平椭球不确定集误差时本文算法最大输出SINR低于目标确定已知条件，这是由于目标脉冲响应不确定造成的失配损失。在相同的不确定集条件下，本文算法高于文献[19]算法输出SINR。

图4 3种情况SINR与迭代次数关系曲线(CNR=5 dB,=0.01)

图5给出了优化后的最优发射波形和最优接收波形，可以看出发射波形矢量和接收波形矢量均包含4个不同的波形。

图5 原始发射波形及优化后的发射波形和接收波形

实验2 不同杂噪比对优化波形设计性能的影响 图6给出了目标脉冲响应存在于扁平椭球不确定集时，3种不同算法在不同杂噪比(CNR)条件下的SINR改善情况。图中横坐标表示CNR，纵坐标表示波形优化后的输出SINR，从图中可以看出，3种算法输出SINR随着CNR的增大而降低。在同一个CNR条件下，当目标脉冲响应为确定值时，输出SINR最大，当目标脉冲响应约束于椭球不确定集中时，文献[19]算法在目标失配条件下具有一定的稳健性，但是仍然存在较大的失配损失。本文算法在目标脉冲响应不确定时采用了迭代鲁棒最小方差法，利用较小的不确定集迭代搜索期望的目标脉冲响应，降低了不确定集导致的SINR损失。

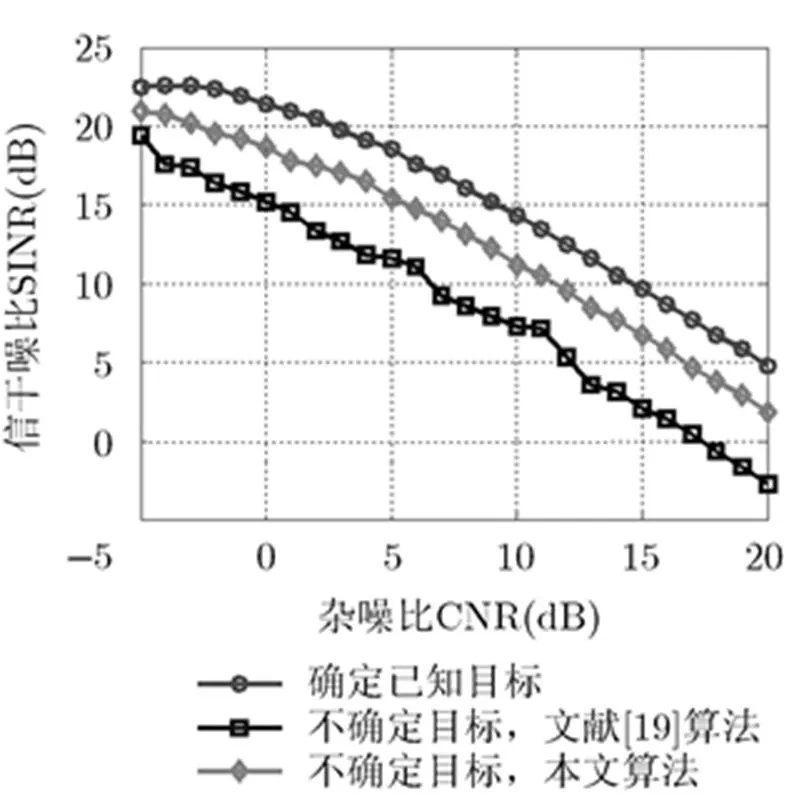
图6 3种算法不同CNR条件下的SINR输出(=0.01)

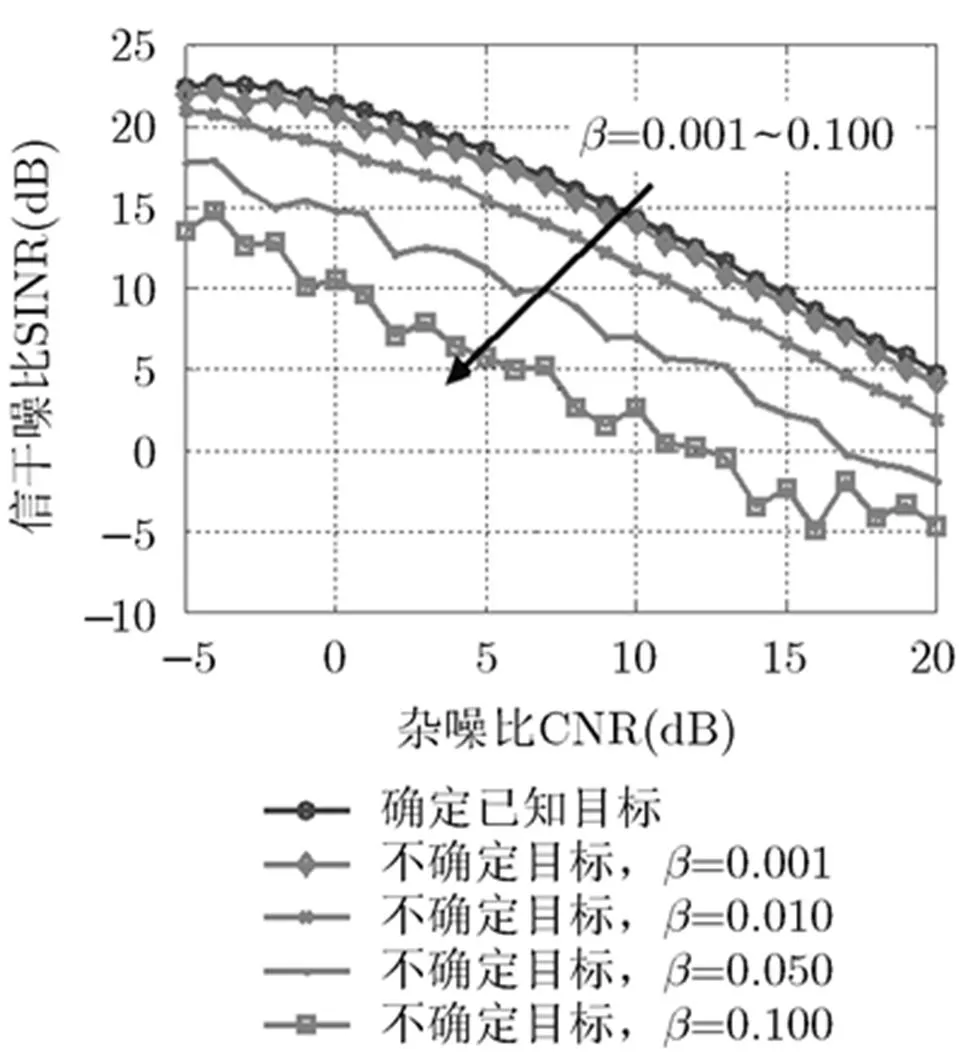
图7 不同不确定系数时输出SINR随CNR的变化曲线

实验3 目标存在于球体不确定集时算法性能分析 当式(11)中时，扁平椭球不确定集退化为球体不确定集合，可以表示为

图8给出了3种不同条件下一次迭代过程SINR收敛曲线，可以看出确定目标SINR输出最大，本文算法和文献[19]算法非常接近，本文算法虽然存在一定的失配损失，但是由于IRMVB处理步骤降低了失配损失，使得整体输出结果与文献[19]算法性能相当，具有较强的稳健性。

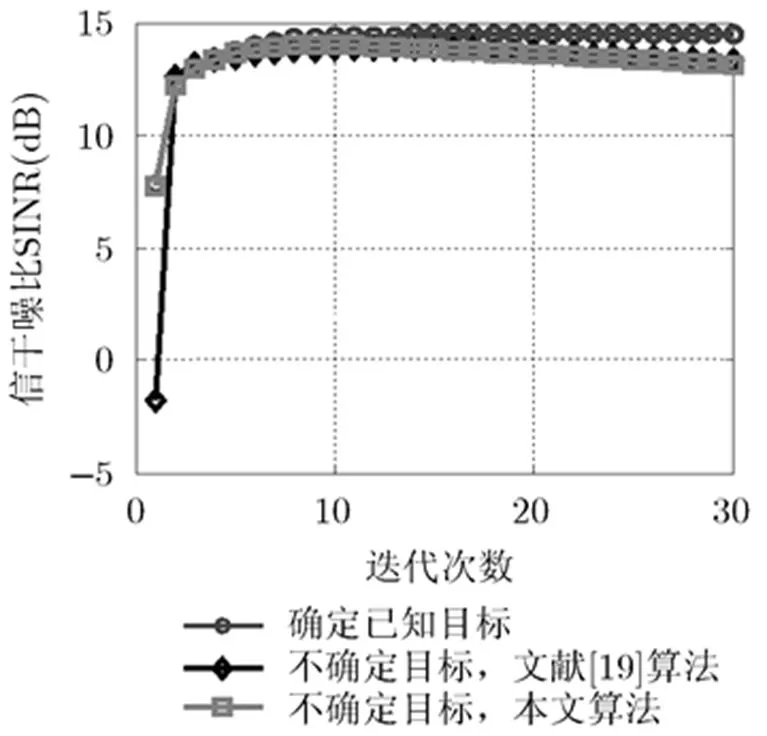
图8 3种情况SINR与迭代次数关系曲线(CNR=5 dB,=0.01)

图9给出了目标脉冲响应存在于球体不确定集时，3种不同算法在不同杂噪比(CNR)条件下的SINR改善情况。图中横坐标表示CNR，纵坐标表示波形优化后的输出SINR，从图中可以看出，3种算法输出SINR随着CNR的增大而降低。在同一个CNR条件下，当目标脉冲响应为确定值时，输出SINR最大，当目标脉冲响应约束于球体不确定集中时，文献[19]算法能够匹配球体不确定集，本文算法存在模型失配损失，但在目标脉冲响应不确定时采用了迭代鲁棒最小方差法，利用较小的不确定集迭代搜索期望的目标脉冲响应，降低了不确定集模型失配导致的SINR损失。从图中可以看出，本文算法在模型失配时相对于文献[19]算法存在约0.4 dB的损失。

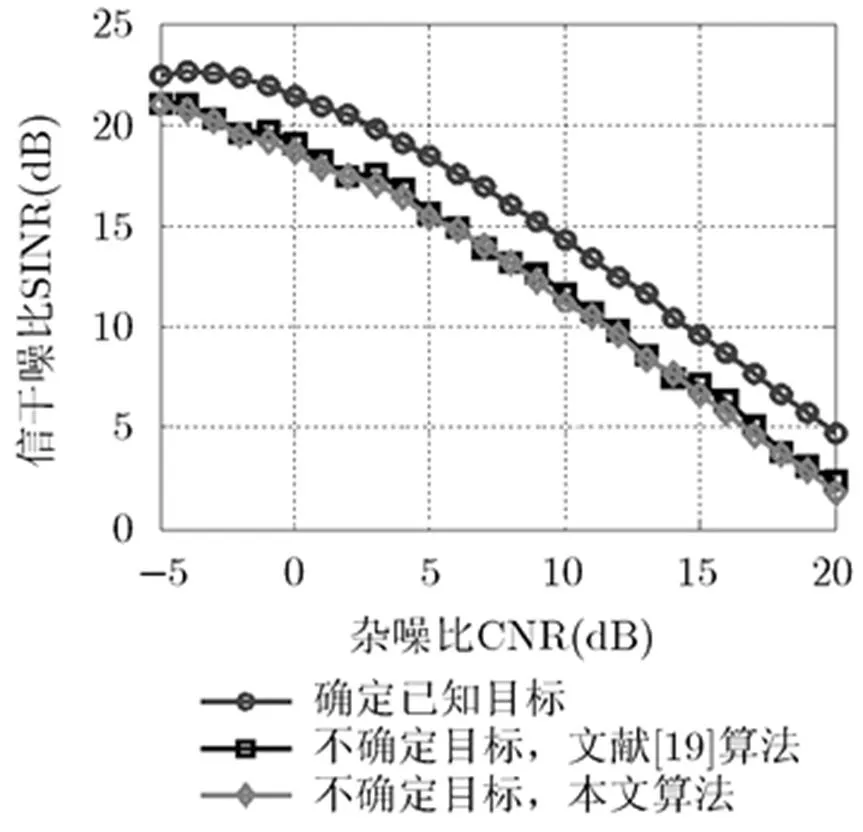
图9 3种算法不同CNR条件下的SINR输出(=0.01)

5 结论

本文在MIMO雷达联合发射-接收波形优化设计过程中，将目标脉冲响应的误差推广到更为一般的扁平椭球不确定集约束条件，并利用Lagrange乘子法对优化过程进行推导，得出扁平椭球不确定集约束下的闭式表达式，将不确定集约束下的优化问题转化成简单的线性搜索问题，为了提高目标脉冲响应不确定集范围较大时的优化性能，采用了迭代鲁棒最小方差法进行求解，进一步提高了波形设计改善性能，并指出了基于扁平椭球不确定集约束条件的优化问题与球体约束条件优化问题的内在联系，最后通过仿真结果验证了本文算法对于目标不确定性的稳健性。

参考文献

[1] ROMERO R A, BAE J, and GOODMAN N A.Theory and application of SNR and mutual information matched illumination waveforms[J]., 2011, 47(2): 912-927.

[2] JIU Bo, LIU Hongwei, ZHANG Lei,. Wideband cognitive radar waveform optimization for joint target radar signature estimation and target detection[J]., 2015, 51(2): 1530-1546.

[3] JIU Bo, LIU Hongwei, WANG Xu,. Knowledge-based spatial-temporal hierarchical MIMO radar waveform design method for target detection in heterogeneous clutter zone[J]., 2015, 63(3): 543-554.

[4] SEN S. PAPR-constrained pareto-optimal waveform design for OFDM-STAP radar[J]., 2014, 52(6): 3658-3669.

[5] SUN Shunqiao and PETROPULU A P. Waveform design for MIMO radars with matrix completion[J]., 2015, 9(8): 1400-1414.

[6] 纠博, 刘宏伟, 胡利平, 等. 针对目标识别的波形优化设计方法[J]. 电子与信息学报, 2009, 31(11): 2585-2590.

JIU Bo, LIU Hongwei, HU Liping,. A method of waveform design for the recognition of radar targets[J].&, 2009, 31(11): 2585-2590.

[7] AUBRY A, DE MAIO A, FARINA A,. Knowledge- aided (potentially cognitive) transmit signal and receive filter design in signal-dependent clutter[J]., 2013, 49(1): 93-116.

[8] AUBRY A, DE MAIO A, JIANG Bo,.. Ambiguity function shaping for cognitive radar via complex quartic optimization[J]., 2013, 61(22): 5603-5619.

[9] HAYKIN S. Cognitive radar: a way of the future[J]., 2006, 23(1): 30-40.

[10] FATEMI M and HAYKIN S. Cognitive control: Theory and application[J]., 2014, 2: 698-710.

[11] SIRA S P, COCHRAN Do, SUPPAPPOLA A P,. Adaptive waveform design for improved detection of Low-RCS targets in heavy sea clutter[J]., 2007, 1(1): 56-66.

[12] GARREN D A, OSBORN M K, ODOM A C,. Enhanced target detection and identification via optimised radar transmission pulse shape[J].,, 2001, 148(3): 130-138.

[13] HERBERT G M. Clutter modelling for space-time adaptive processing in airborne radar[J].,&, 2009, 4(2): 178-186.

[14] JIAN L, STOICA P, and WANG Z S. Doubly constrained robust capon beamformer[J]., 2004, 52(9): 2407-2423.

[15] JIAN Li and STOICA P. On robust capon beamforming and diagonal loading[J]., 2003, 51(7): 1702-1715.

[16] NAI S E, SER W, ZHU Liangyu,. Iterative robust minimum variance beamforming[J]., 2011, 59(4): 1601-1611.

[17] LORENZ R G and STEPHEN P B. Robust Minimum Variance Beam forming[J]., 2005, 53(5): 1684-1696.

[18] 杜兰. 雷达高分辨距离像目标识别方法研究[D]. [博士论文], 西安电子科技大学, 2007.

DU Lan. Study on radar HRRP target recognition[D]. [Ph. D. dissertation], Xidian University, 2007.

[19] CHEN Chunyang and VAIDYANATHAN P P. MIMO radar waveform optimization with prior information of the extended target and clutter[J]., 2009, 57(9): 3533-3544.

[20] 戴凌燕, 王永良, 李荣锋, 等. 基于不确定集的稳健Capon波束形成算法性能分析[J]. 电子与信息学报, 2009, 31(12): 2931-2936.

DAI Lingyan, WANG Yongliang, LI Rongfeng,. Performance analysis of robust capon beamforming based on uncertainty set[J].&, 2009, 31(12): 2931-2936.

Robust MIMO Radar Waveform Design Algorithm Based on Uncertainty Set

LI Xiuyou XUE Yonghua HUANG Yong GUAN Jian

(,,264001,)

In order to solve the problem of performance losses in the MIMO radar waveform design when target signal is uncertainty, a novel joint optimization of transmitting waveforms and receiving filters in the MIMO radar for the case of target in flat ellipsoid uncertainty set is proposed. Firstly, constraint of impulse response of target is extended to flat ellipsoid uncertainty set, Lagrange multiplier is used to solve the optimization problem, and the closed form solution is got under the constrain. Secondly, in order to improve SINR output of waveform design when the uncertainty set is large, Iterative Robust Minimum Variance Beamforming (IRMVB) is used to get more precise target impulse response. Thirdly, the relationship between flat ellipsoid uncertainty set and sphere uncertainty set is analyzed, and a solution which has the form of diagonal loading is derived. Finally, simulation results show that the proposed algorithm has excellent performance and it is robust for the uncertainty of impulse response of the target.

MIMO radar; Waveform design; Flat ellipsoid; Lagrange function

TN958

A

1009-5896(2016)10-2445-08

10.11999/JEIT151425

2015-12-14；改回日期：2016-05-30；网络出版：2016-07-14

李秀友 lixiuyou2012@163.com

国家自然科学基金(61471382, 61401495, 61501487, 61531020)，山东省自然科学基金(2015ZRA06052)

The National Natural Science Foundation of China (61471382, 61401495, 61501487, 61531020), The Natural Science Foundation of Shandong Province (2015ZRA06052)

李秀友： 男，1983 年生，博士生，研究方向为认知雷达波形设计、海杂波中目标检测等.

薛永华： 男，1986 年生，博士生，研究方向为MIMO雷达波形设计及目标检测等.

黄 勇： 男，1979 年生，博士，研究方向为MIMO雷达波形设计及目标检测等.

关 键： 男，1968 年生，教授，博士生导师，研究方向为雷达目标检测与跟踪、侦察图像处理和信息融合等.