矢量传感器阵列MIMO雷达高精度二维DOA与极化联合估计

梁 浩 崔 琛 余 剑 郝天铎



矢量传感器阵列MIMO雷达高精度二维DOA与极化联合估计

梁 浩*崔 琛 余 剑 郝天铎

(合肥电子工程学院通信对抗系 合肥 230037)

该文采用矢量传感器配置下的十字型阵列MIMO雷达系统，提出一种新的2维高精度DOA与极化参数联合估计算法。首先根据MIMO雷达虚拟阵列导向矢量的特点，通过降维矩阵的设计及回波数据的降维变换，将高维回波数据转换至低维信号空间；然后基于传播算子获得对应信号子空间的估计，利用收、发阵列阵元间长基线对应的旋转不变性和极化矢量中电场矢量和磁场矢量的叉积进行2维高精度DOA估计和解模糊处理，同时利用与阵列结构无关的极化域旋转不变性进行极化辅角和极化相位差的联合估计。该矢量传感器MIMO雷达阵列可同时获取MIMO雷达的波形分集和矢量传感器的极化分集，无需额外增加阵元和硬件开销，能够有效扩展阵列孔径，提高参数估计性能；同时通过降维变换及传播算子，在获取信噪比增益的同时，能够实现2维高精度DOA和2维极化矢量的联合估计及参数的自动配对，有效降低数据处理维数和参数估计的运算复杂度；最后，仿真结果验证了理论分析的正确性和算法的有效性。

MIMO雷达；矢量传感器阵列；高精度DOA估计；极化参量

1 引言

多输入多输出(Multiple Input and Multiple Output, MIMO)雷达在目标检测、参数估计、杂波抑制等方面具有诸多优势[1,2]，已成为现代雷达发展趋势的综合体现，引起国内外学者的高度关注。

单基地MIMO雷达因其虚拟扩展能力，能够获取比传统相控阵雷达更大的虚拟孔径，因此在参数估计性能方面优势明显。鉴于虚拟扩展后与1维线性阵列的等效相似性，目前的研究大多是将传统基于相控阵雷达的高分辨算法直接推广应用，获取目标1维方位测向，而无法进行目标方向的定位。事实上，当收、发阵列均采用2维(或更高维)阵列配置时，目标参数维度的扩展意味着目标特征描述得更加准确，同时收、发阵列经过MIMO雷达虚拟扩展后整体天线流型也就更为复杂，因此深入研究2维天线配置下单基地MIMO雷达的虚拟扩展性能以及参数估计问题对目标的定位具有重要意义。文献[7]研究了双平行线阵配置下单基地MIMO雷达的2维参数估计问题，但双平行线阵配置只能实现1维方向上的阵列扩展；文献[8,9]研究了L型阵列配置下单基地MIMO雷达的2维参数估计问题，并提出了对应的参数估计算法；文献[10]研究了平面阵配置下的单基地MIMO雷达的2维参数估计问题，并针对降维后阵列流型与双基地MIMO雷达的等效相似性，利用文献[11,12]中的酉变换思想进行实数域信号子空间估计和2维参数求解，但其降维矩阵的设计以及降维过程本质上为文献[3-6]中1维降维变换在2维上的扩展应用，同时面临着巨大硬件成本和复杂代价。以上算法尽管能够实现单基地MIMO雷达1维/2维目标角度的有效估计，但大多要求收、发阵列阵元间距满足半波长的限制，本质上仍属于角度参量在短基线阵元间距上的度量。

电磁矢量传感器因其能够获得极化分集，有效提高系统性能，而被广泛应用于无线通信与信号处理中；文献[13-17]研究表明MIMO雷达与矢量传感器相结合能够综合极化分集与波形分集，有效提高系统辨识和目标分辨能力，但接收端线阵配置的矢量传感器只用到了电磁的两维信息；文献[18,19]基于发射极化利用玻印亭矢量获取目标2维角度估计，并利用了6维电磁信息提高参数估计性能，却弱化了收发阵列流型对测向的作用，同时未对极化参量进行有效估计。本文针对单基地MIMO雷达的多维参数联合估计问题，采用矢量传感器配置下的十字型阵列MIMO雷达系统，提出一种2维高精度DOA与极化参数联合估计算法，并通过仿真验证本文理论分析的正确性和算法的有效性。

2 信号模型

考虑收、发共址的MIMO雷达系统，收、发阵列均为十字型阵列配置，其中十字型阵列由平面上以参考点为交叉点的两个垂直等间距线阵构成，并以参考点(点为轴，轴共用)对称分布着和个阵元，即轴与轴的各个半轴(含参考点)的阵元数分别为和，其中阵元间距分别为和。收、发阵列配置如图1所示，其中发射阵列由标量传感器构成，接收阵列由共点式电磁矢量传感器构成，每个矢量传感器由三正交偶极子组成。假设远场空域存在个不相关目标，第目标对应的俯仰和方位角为，极化辅角与极化相位为；发射端个标量传感器发射相同载频及带宽的正交信号，即，其中第个发射阵元的发射信号，其中，；则第次脉冲下发射波形经过目标反射后在接收端的输出信号为

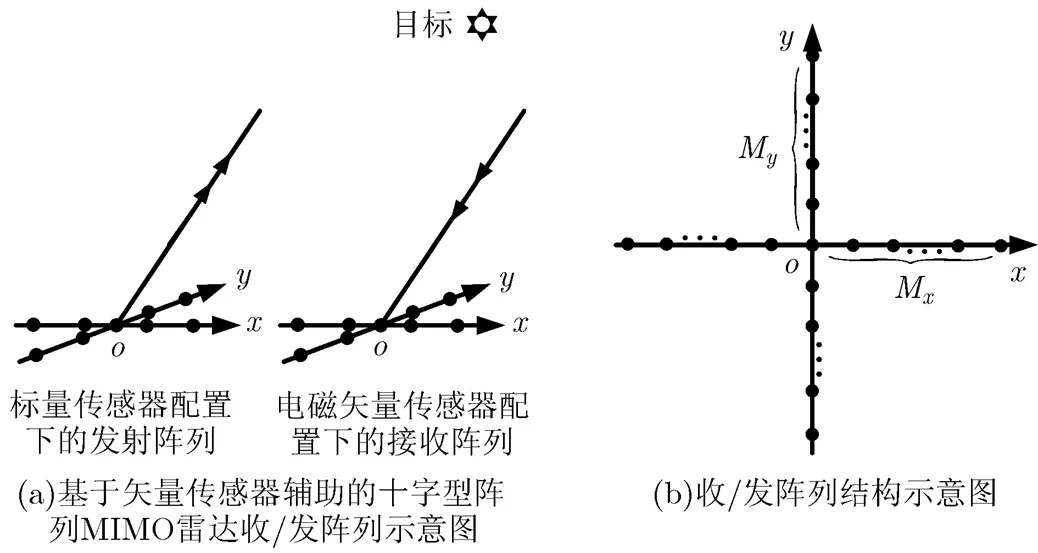
图1 矢量传感器阵列MIMO雷达收、发十字型阵列配置

式中，

3 矢量传感器MIMO雷达2维高精度DOA与极化联合估计

3.1 接收数据降维预处理

3.2基于传播算子的信号子空间估计

3.3高精度2维DOA估计与极化联合估计

3.3.1 2维方位余弦的粗估计与精估计 由于共点式电磁矢量传感器有3个正交的电偶极子和3个正交的磁环构成，同时极化矢量中电场矢量和磁场矢量的叉积计算得到闭式且自动配对的2维方位角度估计值，因此可以通过对极化矢量进行估计来获取目标的2维方位角度。由式(2)可得，第目标对应的极化矢量可以表示为

综合以上分析可得

进一步可得

化简可得

则对应的无模糊高精度2维方位、俯仰估计值为

3.3.2极化辅角与极化相位联合估计 由式(2)可得，三正交偶极子构成的矢量传感器中，电场与磁场分量在轴的分量具有极化域旋转不变性，由式(12)定义电场与磁场分量在轴的比值为极化因子，即

4 算法性能分析

4.1 降维处理信噪比增益

与文献[20]类似可得，本文经过降维处理前后获得的信噪比增益为

4.2算法复杂度分析

本节主要比较本文算法与文献[10,14]算法的运算复杂度。其中文献[10]RD-Unitary-ESPRIT算法收、发阵列均采用标量传感器配置的矩形阵列，算法总的运算复杂度为：。文献[14]RD-MUSIC算法总的运算复杂度为(为谱搜索步数)。本文算法总的运算量为：。其中,,,,,,,，为了在相同孔径下比较不同算法间的运算复杂度，假设,，显然与文献算法相比，本文算法通过降维变换，同时采用传播算子估计信号子空间，无需特征分解，具有更低的运算复杂度。

5 仿真实验与分析

假设十字型阵列配置下的共址MIMO雷达，雷达收发阵列结构如图1所示，其中接收阵列采用三正交偶极子构成的共点式电磁矢量传感器，以Hadamard编码信号为发射波形，分别进行以下仿真实验。

实验1 算法有效性验证 假设MIMO雷达收、发阵列配置满足，收、发阵元间距为；远场空域存在个独立目标，对应的俯仰、方位2维角度为,；对应的极化辅角和极化相位为,；信噪比，数据快拍为，进行200次Monte-Carlo实验，仿真结果如图2所示。显然，本文算法能够实现目标2维方位角度和2维极化参数的有效估计及参数的自动配对，同时估计的2维方位角度和2维极化参数比较集中而没有出现散布，一定程度上也反映了算法的稳健性。

图2 本文算法2维参数的联合估计结果

实验2 算法估计性能的比较 假设MIMO雷达收、发阵列配置满足，即；远场空域存在个独立目标，俯仰、方位角和2维极化参数为,,；数据快拍为，其余条件不变，进一步与文献[21,22]ESPRIT算法、文献[12]Unitary-ESPRIT算法、文献[10]RD-Unitary- ESPRIT算法及文献[14] RD-MUSIC算法进行参数估计性能的比较；仿真结果如图3所示，其中CRB采用文献[15]推导方式。同时为了获得相同的孔径，ESPRIT, Unitary-ESPRIT及RD-MUSIC算法采用的均匀线阵；RD-Unitary- ESPRIT算法中收、发阵列均采用方形阵，收、发阵列配置，即。由图3仿真结果可知，随着信噪比的增大，以上几种算法参数估计的RMSE逐渐变小，估计精度越来越高，这一点很好理解；与文献算法仅利用阵元间距短基线(半波长)进行参数估计相比，本文算法通过扩展阵元间基线长度来获取2维DOA的高精度估计，同时利用采用三正交偶极子的矢量传感器获得2维DOA的无模糊快速估计，进一步解决高精度DOA的周期模糊，最终获取无模糊的高精度2维DOA估计，估计精度要优于文献算法；同时与文献[10]收发均采用方形阵列相比，本文采用收发十字型阵列在获取2维平移不变性的同时，能够有效减少收发阵元数目，提高阵元利用效率；此外三正交偶极子构成的矢量传感器具有极化域旋转不变特性，可以用来获取极化辅角与极化相位的联合估计，与采用RD-MUSIC算法性比，本文算法无需谱搜索，在获得接近与RD-MUSIC算法的估计精度，具有更低的运算复杂度。

图3 不同算法间多维参数的联合估计性能与信噪比的关系

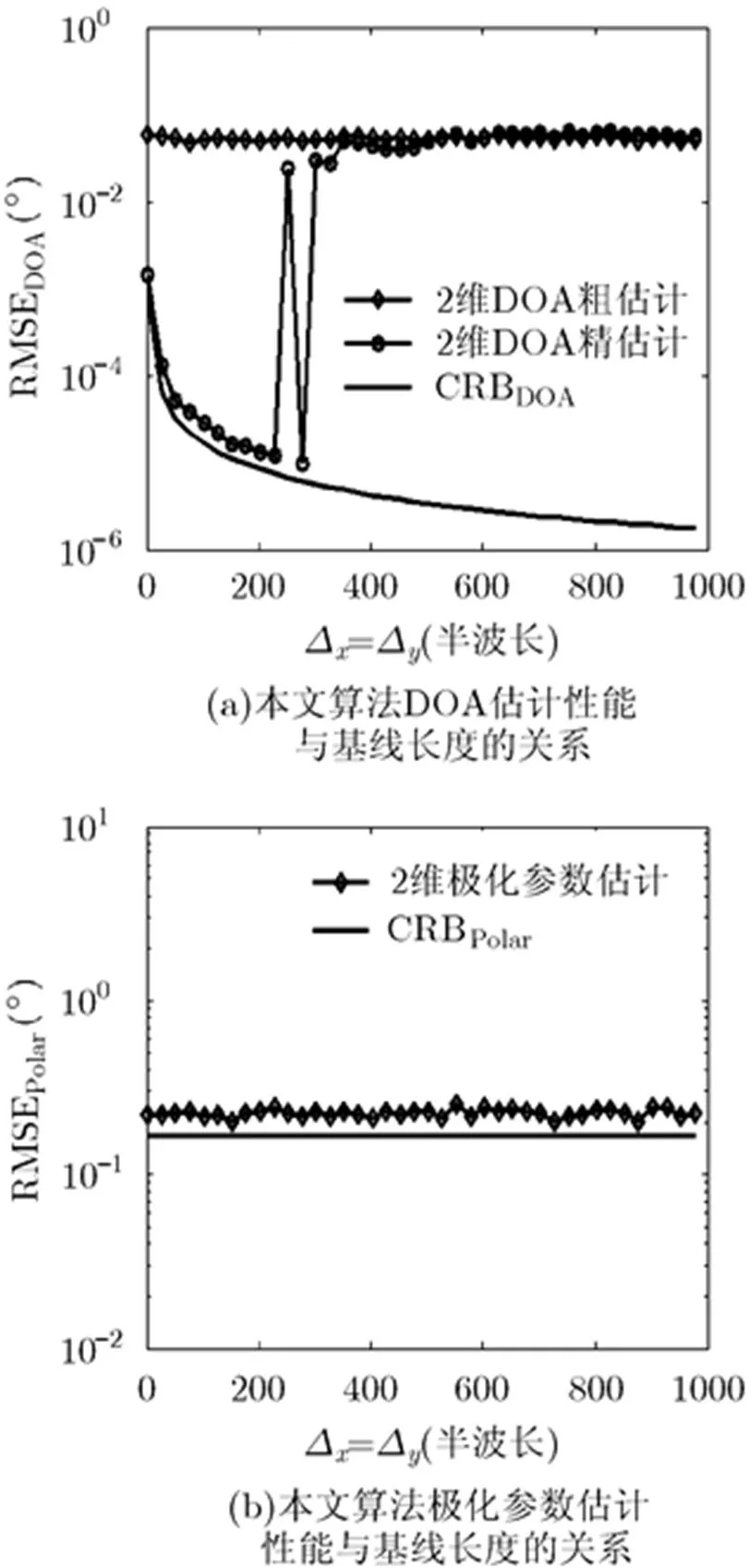
图4 本文算法多维参数估计性能与基线长度()间的关系

6 结论

本文针对单基地MIMO雷达的多维参数联合估计问题，基于矢量传感器配置下的十字型阵列MIMO雷达系统，提出一种2维高精度DOA与极化参数联合估计算法。理论分析和实验仿真表明，算法通过降维变换和传播算子算法，有效降低数据处理维数和算法运算复杂度的同时，能够获得较高的信噪比增益；在获取2维无模糊高精度DOA与2维极化参数联合估计的同时，能够实现参数的自动配对；该矢量传感器MIMO雷达阵列，可同时获取MIMO雷达的波形分集和矢量传感器的极化分集，无需额外增加阵元和硬件开销，即可有效扩展阵列孔径，提高参数估计性能。值得注意的是，本文分析基于收、发十字型阵列配置的矢量阵列MIMO雷达，当收、发阵列采用诸如矩形、L型等平面阵列配置时，算法同样适用。

参考文献

[1] HULEIHEL W, TABRIKIAN J, and SHAVIT R. Optimal adaptive waveform design for cognitive MIMO radar[J]., 2013, 61(20): 5075-5089. doi: 10.1109/TSP.2013.2269045.

[2] WANG P, LI H B, and HIMED B. A parametric moving target detector for distributed MIMO radar in non- homogeneous environment[J]., 2013, 61(9): 2282-2294. doi: 10.1109/TSP.2013. 2245323.

[3] ZHANG X, HUANG Y, CHEN C,. Reduced-complexity Capon for direction of arrival estimation in a monostatic multiple -input multiple-output radar[J]., 2012, 6(8): 796-801. doi: 10.1049/iet-rsn. 2011.0343.

[4] ZHANG X and XU D. Low-complexity ESPRIT-based DOA estimation for colocated MIMO radar using reduced- dimension transformation[J]., 2011, 17(47): 283-284. doi: 10.1049/el.2010.3279.

[5] 文才, 王彤. 单基地MIMO雷达降维酉ESPRIT算法[J].系统工程与电子技术, 2014, 36(6): 1062-1067. doi: 10.3969/j.issn. 1001- 506X.2014.06.08.

WEN C and WANG T. Reduced-dimensional unitary ESPRIT algorithm for monostatic MIMO radar[J]., 2014, 36(6): 1062-1067. doi: 10.3969/j.issn.1001-506X.2014.06.08.

[6] WANG W, WANG X, SONG H,. Conjugate ESPRIT for DOA estimation in monostatic MIMO radar[J]., 2013, 93(7): 2070-2075. doi: 10.1016/j.sigpro. 2013.01.007.

[7] LI J F, ZHANG X F, CHEN W Y,. Reduced- dimensional ESPRIT for direction finding in monostatic MIMO radar with double parallel uniform linear arrays[J]., 2014, 77(1): 1-19. doi: 10.1007/s11277-013-1491-3.

[8] 王伟, 王晓萌, 李欣, 等. 基于MUSIC算法的L型阵列MIMO雷达降维DOA估计[J]. 电子与信息学报, 2014, 36(8): 1954-1959. doi: 10.3724/SP.J.1146.2013.01281.

WANG W, WANG X M, LI X,. Reduced-dimensional DOA estimation based on MUSIC algorithm in MIMO radar with L-shaped array[J].&, 2014, 36(8): 1954-1959. doi: 10.3724/ SP.J.1146. 2013.01281.

[9] 梁浩, 崔琛, 代林, 等. 基于ESPRIT算法的L型阵列MIMO雷达降维DOA估计[J]. 电子与信息学报, 2015, 37(8): 1928-1935. doi: 10.11999/JEIT141295.

LIANG H, CUI C, DAI L,. Reduced-dimensional DOA estimation based on ESPRIT algorithm in MIMO radar with L- shaped array[J].&, 2015, 37(8): 1928-1935. doi: 10.11999/JEIT141295.

[10] LI J F and ZHANG X F. Unitary reduced-dimensional estimation of signal parameters via rotational invariance techniques for angle estimation in monostatic multiple-input-multiple-output radar with rectangular arrays [J].,, 2014, 8(6): 575-584. doi: 10.1049/iet-rsn.2013.0269.

[11] ZHENG G M and CHEN B X. Unitary dual-resolution ESPRIT for joint DOD and DOA estimation in bistatic MIMO radar[J]., 2015, 26(1): 159-178. doi: 10.1007/s11045-013-0244-5.

[12] ZHENG G M, CHEN B X, and YANG M L. Unitary ESPRIT algorithm for bistatic MIMO radar[J]., 2012, 48(3): 179-181. doi: 10.1049/el.2011.3657.

[13] JIANG H, WANG D F, and LIU C. Joint estimation of DOD/DOA/polarization parameters of bistatic MIMO radar[J]., 2010, 17(5): 32-37. doi: 10.1016/S1005- 8885(09)60504-5.

[14] ZHOU M and ZHANG X F. Joint estimation of angle and polarization for bistatic MIMO radar with polarization sensitive array using dimension reduction MUSIC[J]., 2015, 81(3): 1333-1345. doi: 10.1007/s11277-014- 2187-z.

[15] 王克让, 朱晓华, 何劲. 基于矢量传感器MIMO雷达的DOD/DOA和极化联合估计算法[J]. 电子与信息学报, 2012, 34(1): 160-165. doi: 10.3724/SP.J.1146.2011.00576.

WANG K R, ZHU X H, and HE J. Joint DOD DOA and polarization estimation for MIMO radar with electromagnetic vector sensors[J].&, 2012, 34(1): 160-165. doi: 10.3724/ SP.J.1146.2011.00576.

[16] 王克让, 何劲, 贺亚鹏, 等. 基于矢量传感器的扩展孔径双基地MIMO 雷达多目标定位算法[J]. 电子与信息学报, 2012, 34 (4): 582-586. doi: 10.3724/SP.J.1146.2011.00801.

WANG K R, HE J, HE Y P,. Extended-aperture mulit-target location algorithm for MIMO radars with vector sensors[J].&, 2012, 34(4): 582-586. doi: 10.3724/SP.J.1146.2011.00801.

[17] 郑桂妹, 杨明磊, 陈伯孝, 等. 干涉式矢量传感器MIMO雷达的DOD/DOA和极化联合估计[J]. 电子与信息学报, 2012, 34(11): 2635-2641. doi: 10.3724/SP.J.1146.2012.00407.

ZHENG G M, YANG M L, CHEN B X,. Joint DOD/DOA and polarization estimation for interferometric MIMO radar with electromagnetic vector sensors[J].&, 2012, 34(11): 2635-2641. doi: 10.3724/SP.J.1 146.2012.00407.

[18] GU C, HE J, Li H,. Target localization using MIMO electromagnetic vector array systems[J]., 2013, 93(7): 2103-2107. doi:10.1016/j.sigpro.2013.02.005.

[19] 郑桂妹, 陈伯孝, 杨明磊. 基于矢量传感器MIMO雷达的发射极化优化DOA估计算法[J]. 电子与信息学报, 2014, 36(3): 565-570. doi: 10.3724/SP.J.1146.2013.00648.

ZHENG G M, CHEN B X, and YANG M L. Transmitted polarization optimization for DOA estimation based on vector sensor MIMO radar[J].&, 2014, 36(3): 565-570. doi: 10.3724/ SP.J.1146.2013.00648.

[20] 梁浩, 崔琛, 余剑. 基于ESPRIT算法的十字型阵列MIMO雷达降维DOA估计[J]. 电子与信息学报, 2016, 38(1): 80-89. doi: 10.11999/JEIT150402.

LIANG H, CUI C, and YU J. Reduced-dimensional DOA stimation based on ESPRIT algorithm in monostatic MIMO radar with cross array [J].&, 2016, 38(1): 80-89. doi: 10.11999 /JEIT150402.

[21] CHEN D F, CHEN B X, and GUO D Q. Angle estimation using ESPRIT in MIMO radar[J]., 2008, 44(12): 770-771. doi: 10.1049/el:20080276.

[22] CHEN J L, GU H, and SU W M. Angle estimation using ESPRIT without pairing in MIMO radar[J]., 2008, 44(24): 1422-1423. doi: 10.1049/el:20089089.

[23] LEMMA A N, VEEN A J, and DEPRETTERE E F. Multiresolution ESPRIT algorithm[J]., 1999, 47(6): 1722-1726. doi: S 1053-587X (99)03682-X.

Joint Estimation of Two Dimensional DOA with High Accuracy and Polarization for MIMO Radar Using Electromagnetic Vector Sensor Arrays

LIANG Hao CUI Chen YU Jian HAO Tianduo

(,,230037,)

In this paper, monostatic MIMO radar with cross array using electromagnetic vector antennas is utilized and a novel algorithm for fast Two Dimensional (2D) Direction Of Arrival (DOA) with high accuracy and polarization estimation is proposed. First, given the virtual steering vector of monostatic MIMO radar, a reduced-dimensional matrix is employed and the high dimensional received data is transformed into a lower dimensional signal space via the reduced-dimensional transformation. Then the Propagator Method (PM) is utilized to estimate the corresponding signal subspace by linear operation. Second, rotational invariance relationships with long baseline in the proposed scheme and polarization vector cross product between the normalized electric vector and the normalized magnetic vector can be used to obtain the 2D DOA estimation with high accuracy and non-ambiguity. The polarization rotational invariance relationship, which is irrespective of array geometry, is utilized to estimate the auxiliary polarization angle and polarization phase difference. The proposed system, extending array aperture without increasing sensors and hardware costs, can obtain the waveform diversity offered by MIMO radar and the polarization diversity offered by vector sensor together and achieve better estimation performance. Meanwhile, through the reduced-dimensional and linear operation, the proposed algorithm, obtaining signal to ratio gain and joint estimation for 2D DOA with high accuracy and 2D polarization parameters with automatic pairing, can reduce the dimension of received data and the computational complexity of parameters estimation effectively. Lastly, simulation results verify the correctness of theoretical analysis and the effectiveness of proposed algorithm.

MIMO radar; Vector sensor array; High accurate DOA estimation; Polarization parameters

TN958

A

1009-5896(2016)10-2437-08

10.11999/JEIT151469

2015-12-24；改回日期：2016-07-22；网络出版：2016-08-26

梁浩 lhmailhappy@163.com

国家自然科学基金(60702015)，安徽省科技攻关项目(1310115188)，电子工程学院院控科研基金(KY13A197, KY13A200, KY13A206)

The National Natural Science Foundation of China (60702015), Auhui Province Foundation for Science and Technology Research Project (1310115188), Scientific Research Foundation of Electronic Engineering Institute (KY13A197, KY13A200, KY13A206)

梁 浩： 男，1987年生，博士，主要研究方向为阵列信号处理以及MIMO雷达信号处理.

崔 琛： 男，1962年生，教授，博士生导师，主要研究方向为雷达信号处理.

余 剑： 男，1980年生，讲师，硕士，主要研究方向为雷达信号处理以及雷达对抗技术.

郝天铎： 男，1989年生，博士生，研究方向为认知雷达信号处理.