基于混合匹配追踪算法的MIMO雷达稀疏成像方法

王 伟 张 斌 李 欣



基于混合匹配追踪算法的MIMO雷达稀疏成像方法

王 伟*张 斌 李 欣

(哈尔滨工程大学自动化学院 哈尔滨 150001)

多输入多输出(MIMO)雷达作为一种新型的雷达体制，其成像兼具高分辨率与实时性的优点。由于观测区域的稀疏性，MIMO雷达成像可以用压缩感知的方法进行处理。而现有的MIMO雷达稀疏成像的贪婪恢复算法中，正交匹配追踪算法(OMP)存在成像图像有伪影的缺点，子空间追踪算法(SP)则受到低分辨率的困扰。针对上述问题，该文提出一种称为混合匹配追踪算法的压缩感知贪婪算法以实现MIMO雷达稀疏成像。通过将两种贪婪恢复算法结合起来，利用OMP 算法选择基信号的正交性和SP 算法具有基信号选择的回溯策略，来重构出高分辨率且没有伪影的雷达图像。仿真实验验证了所提算法的有效性。

MIMO雷达；压缩感知；稀疏成像；贪婪算法

1 引言

多输入多输出(MIMO)雷达是一种21世纪新出现的雷达系统[1,2]，它利用多个发射与接收天线同时对目标进行观测。良好的阵列构型设计和波形分集技术使得MIMO雷达能够获得远多于实际物理阵元个数的观测通道和空间自由度，可以显著地改善参数的可辨识性，实现更为灵活的发射方向图设计，改进目标检测和参数估计性能[3]。相比于传统成像雷达，MIMO雷达在成像的方位向分辨率、实时性和运动补偿方面具有明显的性能优势。因此MIMO雷达成像具有广泛的应用前景。

常见的MIMO雷达成像算法，诸如BP(Back Projection)算法[4]或DAS(Delay And Sum)类波束形成算法，包括改进的Kirchhoff偏移算法[5]、衍射堆栈算法[6]等，具有与匹配滤波和波束形成相似的形式，其优点是算法简单易于实现，输出信噪比高，但是存在分辨率较低且旁瓣水平高，成像效果差的缺陷。

为了获得更好的成像效果，人们将压缩感知技术应用到MIMO雷达成像中。稀疏微波成像是指将压缩感知与雷达成像有机结合形成的一种新的成像方法。它通过寻找被观测目标的少量回波数据，利用稀疏重构技术提取目标的空间位置、散射特征和运动特征等参数。和传统的雷达成像算法相比，压缩感知的引入可以显著地降低系统的数据采集率和系统复杂度，而且稀疏重构算法潜在的超分辨能力有进一步提升成像性能的能力。佛罗里达大学的Li教授等人提出了许多适用于MIMO雷达稀疏成像的稀疏重构算法，如循环自适应算法(Iterative Adaptive Approaches, IAA)和稀疏学习循环最小化方法(Sparse Learning via Iterative Minimization, SLIM)等。文献[12]提出了多波形自适应脉冲压缩技术-超分辨率空间谱估计(Multi-waveform Adaptive Pulse Compression, Re-Iterative Super- Resolution, MAPC-RISR)的MIMO雷达2维超分辨率成像算法。这些MIMO雷达成像算法都是将自适应技术应用到2维联合滤波器权矢量的设计中，通过迭代更新2维权矢量和获得的图像幅值，通过一定的迭代次数最终得到高分辨率和低旁瓣的成像结果。但是，这些方法自适应维数巨大，算法的时间复杂度过高，不仅难以进行实时成像，而且在常用的处理器上运行都极为困难。文献[13,14]采用线性规划的方法解决压缩感知问题，得到良好的效果。但是，线性规划的方法有着运算量大，不易工程实现的缺点。文献[15-17]将贝叶斯学习应用到穿墙雷达成像中，但是该算法需要成像场景距离向目标点分布的先验知识，而这在实际应用中大受限制。文献[18]将压缩感知技术与传统的DAS 波束形成算法结合起来进行雷达成像。这种方法在数据恢复和抗干扰方面表现出色，但是由DAS算法带来的低分辨率和高旁瓣问题依然存在。贪婪恢复算法的代表是正交匹配追踪(Orthogonal Matching Pursuit, OMP)类算法，这类算法包括OMP, CoSaMP等。这种算法有着较低的运算负荷，较高的成像分辨率，但是由于OMP算法在基信号选择时只能扩充不能去除不良基信号的策略，OMP类恢复算法在雷达成像应用中会存在伪影点，这不利于目标的识别。文献[22]提出了被称为子空间追踪算法(SP)的压缩感知贪婪算法，纠正了OMP算法中存在伪影点的问题，但是在MIMO雷达成像应用中其分辨率较OMP算法低。

本文提出一种新的压缩感知雷达成像重构算法，称之为混合匹配追踪算法(Hybrid Macthing Pursuit, HMP)。将OMP算法和子空间追踪(Subspace Pursuit, SP)算法的优点结合起来，使得它在选择基信号时保证了正交性，而在支撑集更新时采用回溯策略，并将这种方法应用的MIMO雷达成像场景中。通过这种操作，所提方法在付出一定运算量的代价下可以保证很高的雷达图像重建分辨率，且不会出现伪影现象。仿真实验证明了所提算法的有效性和优越性。

2 MIMO雷达成像模型

图1 单基地MIMO雷达2维成像模型

去载波后，通过相关处理器组(匹配滤波)，利用发射信号的正交性实现通道分离输出的第(,)个通道信号是

对其做傅里叶变换，并且代入路径延迟公式，得到频域形式的输出为

式中，令

式(9)表明，经过匹配滤波后目标的散射系数与第(,)个通道在空间谱的回波满足傅里叶变换关系。设空间谱中每个通道均有个采样样本，则式(9)可表示为向量形式。

以上讨论皆是在连续的散射点空间进行的，而稀疏成像算法都是基于离散化的目标场景网格实现成像，因此设成像场景可以离散化为个网格点，且将个接收阵元的回波列堆栈，并考虑实际噪声的影响，可以得到离散空间的MIMO雷达成像有噪回波模型：

3 基于正交匹配追踪算法和子空间追踪算法的稀疏信号恢复

注意到对于大多数成像场景中，目标区域具有稀疏的特点，亦即散射系数向量中只有有限的几个系数不为零，而压缩感知作为一种稀疏信号处理方法可以有效地解决这类问题。本节介绍两种常用的压缩感知贪婪重构算法，这两种算法也是本文算法的基础。

3.1正交匹配追踪算法

正交匹配追踪算法是一种典型的贪婪重构算法。OMP算法通过每次迭代从观测矩阵中选出与回波或是回波残差相关最大的基信号，将该列扩充到待测信号的支撑集，利用最小二乘法原理消除该列在回波残差的影响，更新回波残差，然后从观测矩阵中去除该列，然后迭代重复，直至算法收敛，迭代结束。设待求信号的总支撑集(即呈现场景内所有的网格点位置)为，非零元的支撑集为，则有，设迭代变量为, OMP算法的具体流程如表1所示。

表1 正交匹配追踪算法

3.2 子空间追踪算法

子空间算法(SP)也是一类基于迭代的贪婪算法。与OMP算法每次迭代过程中选取测量矩阵一个元素不同的是，SP算法每次选取个元素，这样选择的目的是最大可能性地使测量向量在这个元素所张成的子空间内。此外，对基信号的选择首先扩充到2个，然后支撑集的选取就变成从所有2个元素张成的子空间中和测量向量相关性最大的那个子空间。而后，一旦恢复误差达到要求，迭代停止。最终的估计结果和OMP算法相同，也用最小二乘法。具体步骤见表2。

表2 子空间追踪算法

4 基于混合匹配追踪算法的MIMO雷达成像技术

综上，两种贪婪算法的优缺点都很明显，且优势互补。考虑将两种贪婪算法结合起来，以期提高MIMO雷达成像效果。

采用标准OMP算法得到稀疏解的初值且确定初始支撑集。

则残差初始化为

依然采用标准OMP算法对式(15)所求的残差进行处理，可以得到

利用式(16)将支撑集扩充至2个

将原始测量信号向这2个支撑集构成的子空间投影，可以得到更新的支撑集

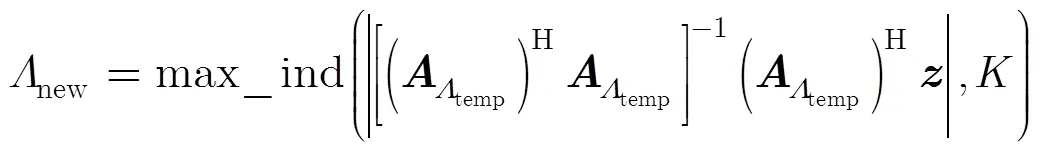
利用式(18)更新残差

所提MIMO雷达稀疏信号恢复算法可以总结如表3所示。

表3 混合匹配追踪算法

从表3的描述来看，HMP算法中的每一次索引选择的过程是利用OMP算法实现的，这种操作保证了在基信号选择时的正交性，也就能在字典矩阵具有傅里叶类似性质的时候可以区分相距很近的空间面元。与此同时，在HMP算法中存在的回溯选择操作与SP算法相同。这种操作的存在保证了HMP算法有能力剔除在前面的迭代过程中被选择的病态的索引，向支撑集中添加新的潜力高的索引。通过以上分析不难看出，HMP算法在理论上比OMP算法和S P算法的性能都要好。

5 仿真实验与分析

仿真实验MIMO雷达的收发阵列都为均匀线阵，4个发射阵元在轴上，坐标设为，接收阵元亦为4个，坐标为。发射波形采用循环算法(Cyclic Algorithm-New,CAN)设计的正交波形，每个发射波形包含码元数为100，载频为10 GHz，带宽设为50 MHz，相应的码元时宽是0.02，脉冲重复周期为6，采样周期等于码元时宽。

5.1 点目标成像仿真

将成像区域网格化。设观测区域由50个距离单元组成，方位角范围为，角度单元设为。考虑两种点目标分布情况。第1种为只有一个点目标，位于第25个距离单元，方位角为；第2种情况有5个目标，呈十字排列，坐标分别为,,,和。所有点目标的后向散射系数都设为1，设噪声为加性高斯白噪声，信噪比为，图2给出了标准OMP算法，SP算法以及本文所提的HMP算法的成像结果。

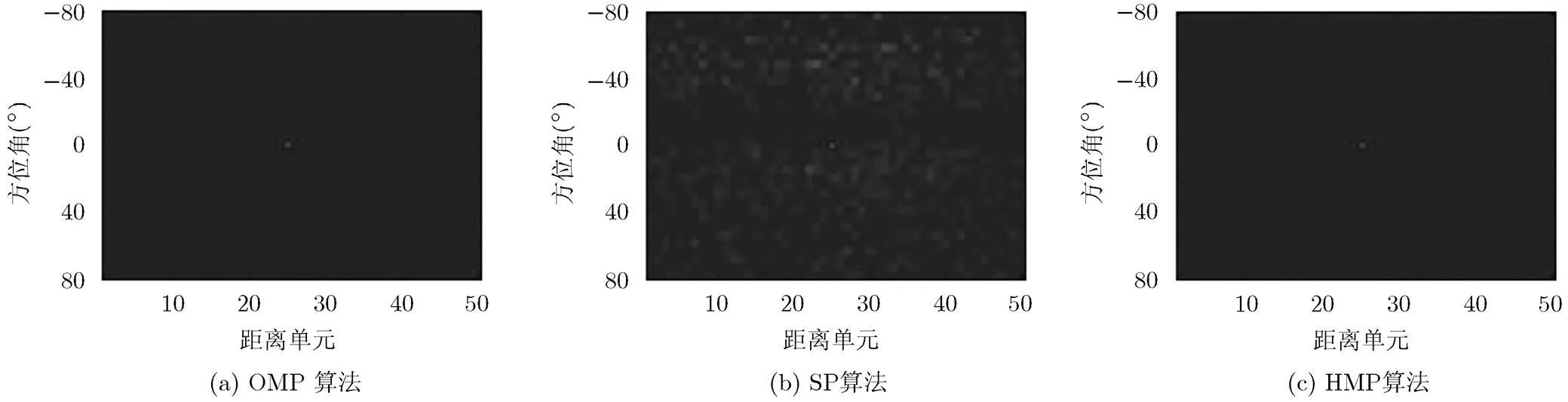
图2 单个点目标时MIMO雷达成像结果

从图2可以看出，对于单个点目标时3种不同的压缩感知恢复算法都在目标位置处形成了尖峰，表明了3种成像算法在单点聚焦成像时的正确性。其中子空间追踪算法(SP)在分辨率和旁瓣水平上没有其它两种贪婪恢复算法表现出色，表现为图2(b)中出现低幅度值的旁瓣，而图2(a)和图2(c)中并没有这种情况。这与前面分析的算法性能是一致的，即SP算法的分辨率要低于OMP算法和本文所提的HMP算法。OMP算法与本文所提的HMP算法成像结果基本相同。在对单点目标成像的应用场景中，OMP算法并没有出现伪影。

图3给出了在多个点目标存在的情况下不同算法的成像结果。为了更直观地比较各种算法的成像性能，图4给出了多个点目标时成像结果的距离向剖面图，对应的距离单元为25。

图3 多个点目标时MIMO雷达成像结果

图4 多个点目标时成像结果的距离向剖面图

从图3和图4可以看出，标准OMP算法在5个点目标位置都形成了峰值，表明OMP算法在多点聚焦成像的可用性。但是存在明显的伪影点，不利于目标的判读。这是由OMP算法对支撑集进行扩充而从不加以删除的策略造成的。而SP算法在5个目标位置也形成了峰值，但是在图像的两端成像质量急剧下降，旁瓣水平较高。这是因为SP算法在迭代过程中，由于一次性选择多个基信号，许多与回波向量高度相关的基信号同时被选取。这种选取策略由于相邻基信号的相关性导致分辨率的损失。HMP算法在5个目标位置处形成峰值，且旁瓣水平和分辨率都较OMP算法和SP算法好。这与前面的分析是一致的。HMP算法中每一次支撑集选择过程是利用OMP算法实现的，这种操作保证了基信号选择的正交性，与此同时，在HMP算法迭代过程中与SP算法类似，可以去除在前面迭代过程中被选择的病态索引，因此HMP算法分辨率更高。

为了说明所提算法抗噪性，图5给出了HMP算法、OMP算法、SP算法以及最近新提出压缩采样修正匹配追踪算法[24](Compressive Sampling Modifying Matching Puresuit, CoSaMMP)和基于变尺度法的贪婪重构算法[25](Variable Metric Method based Gradient Pursuit, VMMGP)在不同信噪比情况下重构误差的表现。设置信噪比从-30 dB增加到30 dB，步长为5 dB，以重构误差作为衡量成像效果的标准。从图5可以看出，这5种信号重构算法的重构误差均随信噪比的提高而减小。当信噪比大于-20 dB时，HMP算法的重构误差要明显小于其它算法，且这5种贪婪重构算法的重构误差均趋于平稳。在这5种算法中，HMP算法的重构误差最小，OMP算法和SP算法重构误差最大，而CoSaMMP算法和VMMGP算法的重构精度虽然由于OMP算法和SP算法，但不及本文所提的HMP算法。这表明HMP算法的抗噪性要优于其它4种贪婪重构算法。

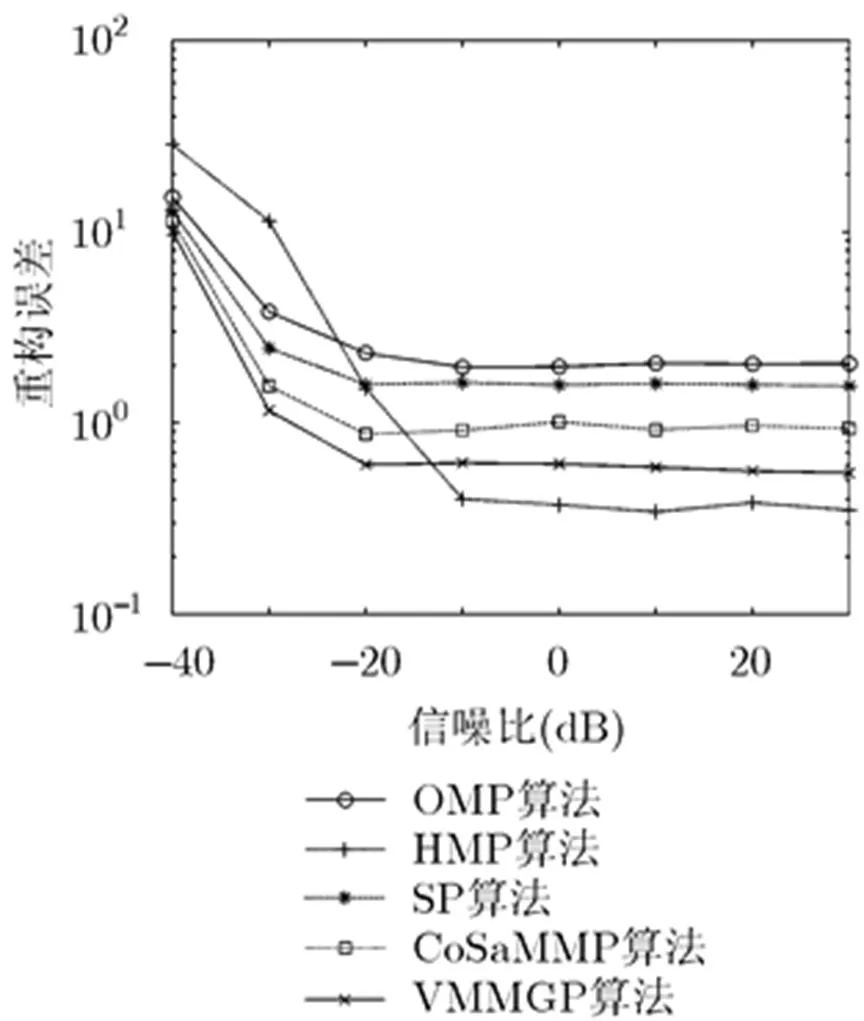
图5几种贪婪重构算法在不同信噪比下的重构误差

5.2 运算时间比较

为了比较不同的贪婪恢复成像算法的运算效率，本文分析不同成像场景时完成所有像素点聚焦成像所需的时间。仿真场景分辨率为50距离元角度元。仿真平台CPU为Intel Core i3-2130，内存为2 G。3种不同的成像算法耗时如表4所示。

表4不同MIMO雷达压缩感知成像算法运算时间比较

从表4可以看出，在相同的成像分辨率应用场景中，对于3种压缩感知恢复算法，在单点目标和多点目标情况下耗时是一样的。而在3种成像算法运算复杂度的比较中，HMP算法的运算时间要明显长于OMP算法和SP算法，后两者的运算时间几乎相同。这与前面算法复杂度分析的结果是一致的。而HMP算法的成像效果是最好的。

6 结论

本文提出了一种混合匹配滤波稀疏信号恢复算法并将其应用到MIMO雷达成像场景中。首先建立了MIMO雷达稀疏成像模型，将雷达图像的聚焦问题转化为稀疏信号的恢复重构问题。通过将OMP算法对基信号选择的正交性和SP算法对基信号选择的回溯特点结合起来，本文所提的HMP算法可以得到高分辨率的成像结果且没有伪影，但是运算量会相应的增大。仿真实验证明了HMP算法可以有效地抑制杂波，消除伪影，从而达到提高MIMO雷达系统对目标检测和识别的性能。

参考文献

[1] FISHLER E, HAIMOVICH A, BLUM R,. MIMO radar: an idea whose time has come[C].IEEE Radar Conference,Philadelphia, PA, USA, 2004: 71-78.

[2] 刘涛. MIMO雷达技术及其应用研究[J]. 无线互联科技, 2015, 6(12): 136-137. doi: 10.3969/j.issn.1672-6944.2015.12.064.

LIU Tao. Research on MIMO radar technology and its application[J]., 2015, 6(12): 136-137. doi: 10.3969/j.issn.1672-6944.2015.12.064.

[3] BLISS D W and FORSYTHE K W. MIMO radar medical imaging: Self-interference mitigation for breast tumor detection[C]. The 40th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 2006: 1558-1562. doi: 10.1109/ACSSC.2006.355020.

[4] 王伟, 马跃华, 王咸鹏. 一种高运算效率的MIMO雷达BP成像算法[J]. 系统工程与电子技术, 2013, 35(10): 2080-2085.

WANG Wei, MA Yuehua, and WANG Xianpeng. High computation effciency BP imaging algorithm for MIMO radar[J]., 2013, 35(10): 2080-2085.

[5] ZHUGE X D, YAROVOY A G, SAVELYEV T,. Modified Kirchhoff migration for UWB MIMO array-based radar imaging[J].,2010, 48(6): 2692-2703. doi: 10.1109/TGRS.2010. 2040747.

[6] OGIWARA S and YAMAKOSHI Y. MIMO radar system for respiratory monitoring using Tx and Rx modulation with M-sequence codes[J]., 2010, 93(9): 2416-2423. doi: 10.1587/ transcom.E93.B.2416.

[7] BARANIUK R and STEEGHS P. Compressive radar imaging[C]. 2007 IEEE Radar Conference, Boston, MA, USA, 2007: 128-133. doi: 10.1109/RADAR.2007.374203.

[8] 杨杰, 廖桂生, 李军. 基于波形选择的MIMO雷达三维稀疏成像与角度误差校正方法[J]. 电子与信息学报. 2014, 36(2): 428-434. doi: 10.3724/SP.J.1146.2013.00500.

YANG Jie, LIAO Guisheng, and LI Jun. Three dimensional MIMO radar imaging using sparse model based on Waveform Selection and Calibration Method in the Presence of Angle Imperfections[J].&,2014, 36(2): 428-434. doi: 10.3724/SP.J.1146. 2013.00500.

[9] 丁丽. MIMO雷达稀疏成像的失配问题研究[D]. [博士论文], 中国科学技术大学, 2014.

DING Li. Ressearch on observation matrix mismatch for MIMO radar sparse imaging[D]. [Ph.D. dissertation], University of Science and Technology of China, 2014.

[10] WILLIAM R, PETRE S, LI J,. Iterative adaptive approaches to MIMO radar imaing[J]., 2010, 4(1): 5-20. doi: 10.1109/JSTSP.2009.2038964.

[11] TAN X, ROVERTS W, LI J,. Sparse learning via iterative minimization with application to MIMO radar imaging[J]., 2010, 59(3): 1088-1101. doi: 10.1109/TSP.2010.2096218.

[12] 王伟, 马跃华, 郝燕玲. 基于MAPC-RISR的MIMO雷达距离-角度二位超分辨率成像算法[J]. 中国科学: 信息科学, 2015, 45(3): 372-384. doi: 10.1360/N112014-00044.

WANG Wei, MA Yuehua, and HAO Yanling. High-resolution MIMO radar range-angle 2D imaging algorithm based on MAPC-RISR[J]., 2015, 45(3): 372-384. doi: 10.1360/N112014-00044.

[13] HIGGINS T, BLUNT S D, SHACKELFORD A K,. Space-range adaptive processing for waveform-diverse radar imaging[C]. IEEE Radar Conference, Arlington, VA, USA, 2010: 321-326. doi: 10.1109/RADAR.2010.5494604.

[14] HUANG Q, QU L, WU B,. UWB through-wall imaging based on compressive sensing[J].,2010, 48(3): 1408-1415. doi: 10.1109/TGRS.2009.2030321.

[15] TANG V H, Bouzerdoum A, Phung S L,. Enhanced through-the-wall radar imaging using Bayesian compressive sensing[C]. SPIE, 2013, 8717: 1-12. doi: 10.1117/12.2014814.

[16] WU Q, ZHANG Y D, AMIN M G,. Through-the-wall radar imaging based on modified Bayesian compressive sensing[C]. IEEE China Summit Internation Conference on Signal Information Process, Xi’an, China, 2014: 232-236. doi: 10. 1109/ChinaSIP.2014.6889238.

[17] WU Q, ZHANG Y D, AMIN M G,. Multi-static passive SAR imaging based on Bayesian compressive sensing[C]. SPIE Compressive Sensing Conference, Valtimore, MD, USA, 2014: 9109. doi: 10.1117/12.2050524.

[18] 庄燕滨, 王尊志, 肖贤建. 基于最大后验概率估计的压缩感知算法[J]. 计算机科学, 2015, 42(11): 279-283.

ZHUANG Yanbin, WANG Zunzhi, and XIAO Xianjian. Reconstruction algorithm in compressed sensing based on maximum posterior estimation[J]., 2015, 42(11): 279-283.

[19] PATI Y C, REZAIIFAR R, KRISHNAPREASAD P S,. Orthogonal matching pursuit: Recursive function approximation with applications to wavelet decomposition [C]. 27th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 1993: 40-44.

[20] TROPP J A and GILBERT A C. Signal recovery from random measurements via orthogonal matching pursuit[J].,2007, 53(12): 4655-4666. doi: 10.1109/TIT.2007.909108.

[21] 晋良念, 钱玉彬, 申文亭. 基于改进OMP的超宽带穿墙雷达稀疏成像方法[J]. 计算机技术与应用, 2015, 41(11): 135-139.

JIN Liangnian, QIAN Yubin, and SHEN Wenting. Sparse imaging for ultra-wideband through-the-wall radar based on modified OMP algorithm[J]., 2015, 41(11): 135-139.

[22] DAI W and MILENKOVIC O. Subspace pursuit for compressive sensing signal reconstruction[J]., 2009, 55(5): 2230-2249. doi: 10.1109/TIT.2009.2016006.

[23] HE H, STOICA P, LI J,. Designing unimodular sequence sets with good correlations-including an application to MIMO radar[J].,2009, 57(11): 4391-4405. doi: 10.1109/TSP.2009.2025108.

[24] 甘伟, 许录平, 张华, 等. 一种贪婪自适应压缩感知重构[J]. 西安电子科技大学学报, 2012, 39(3): 50-57.

GAN Wei, XU Luping, ZHANG Hua,. Greedy adaptive recovery algorithm for compressed sensing[J]., 2012, 39(3): 50-57.

[25] 刘盼盼, 李雷. 王浩宇. 压缩感知中基于变尺度法的贪婪重构算法的研究[J]. 通信学报, 2014, 35(12): 98-115.

LIU Panpan, LI Lei, and WANG Haoyu. Research on gredddy reconstruction algorithms of compressed sensing based on variable metric method[J]., 2014, 35(12): 98-115.

An Imaging Method for MIMO Radar Based on Hybrid Matching Pursuit

WANG Wei ZHANG Bin LI Xin

(,,150001,)

MIMO radar is an emerging radar system that has significant potential. MIMO radar can provide high resolution and real-time imaging solution. Because of the sparsity of the observation zone, the task of MIMO radar imaging can be formulated as a problem of sparse signal recovery based on Compressed Sensing (CS). In MIMO radar imaging application based on CS, existing greedy algorithms, such as the Orthogonal Matching Pursuit (OMP) algorithm and the Subspace Pursuit (SP) algorithm, suffer from artifacts and low-resolution, respectively. To deal with the drawback of existing greedy algorithms, a Hybrid Matching Pursuit (HMP) algorithm is proposed to combine the strengths of OMP and SP. By using of the orthogonality among selected basis-signals and the backtracking strategy for basis-signal reevaluation, the HMP algorithm can reconstruct high-resolution radar image with no artifacts. Simulation results demonstrate the effectiveness and superiority of the proposed algorithm.

MIMO radar; Compressive sensing; Sparse imaging; Greedy algorithm

TN957.52

A

1009-5896(2016)10-2415-08

10.11999/JEIT151453

2015-12-22；改回日期：2016-06-17；网络出版：2016-08-26

王伟 wangwei407@hrbeu.edu.cn

国家自然科学基金(61571148)，中国博士后特别资助(2015T80328)，中国博士后科学基金(2014M550182)，黑龙江省博士后特别资助(LBH-TZ0410)，哈尔滨市科技创新人才专项(2013RFXXJ016)

The National Natural Science Foundation of China (61571148), China Postdoctoral Special Funding (2015T80328), China Postdoctoral Science Foundation (2014M550182), Heilongjiang Province Postdoctoral Special Fund (LBH-TZ0410), Innovation of Science, Technology Talents in Harbin (2013RFXXJ016)

王 伟： 男，1979年生，教授，博士，研究方向为MIMO雷达信号处理、组合导航系统和无线电导航.

张 斌： 男，1989年生，博士生，研究方向为MIMO雷达信号处理、压缩感知应用.