具有数据丢失二维Roesser系统的量化状态反馈控制
2016-10-13卜旭辉程子豪余发山杨俊起
卜旭辉, 程子豪, 余发山, 杨俊起
(河南理工大学电气工程与自动化学院,河南焦作454000)
具有数据丢失二维Roesser系统的量化状态反馈控制
卜旭辉, 程子豪, 余发山, 杨俊起
(河南理工大学电气工程与自动化学院,河南焦作454000)
探讨存在数据丢失二维Roesser系统的量化状态反馈控制器设计问题。假设二维系统在网络控制系统中运行且系统状态全部可测,测量到的状态数据量化后经网络进行传输,同时由于网络自身限制伴随数据包丢失现象的发生。首先将数据丢失描述成取值为0或1的随机伯努利序列,定义了随机意义下二维系统的均方稳定性。其次,采用扇形界方法处理数据量化造成的误差,给出一个闭环系统均方渐进稳定的充分条件,基于该条件可通过求解线性矩阵不等式设计状态反馈控制器。最后,仿真示例验证了所提设计方法的有效性。
二维系统;网络控制系统;量化控制;数据丢失;随机系统
0 引言
二维系统理论在多维数字滤波、图像处理、信号处理、过程控制以及迭代学习控制中有着广泛的应用,目前已经成为控制领域研究的热点[1-4]。二维系统的稳定性分析与镇定、H∞控制、自适应控制、最优保成本控制以及滑模控制等方面已经有较多文献发表,详见文献[5-9]。另一方面,网络控制系统目前在实际中广泛应用,相比与传统的点对点控制模式,网络控制系统具有低成本、安装简便、维护方便以及可靠性高等优点。但网络通信机制的引入,使得控制系统产生一些不确定性的因素,如网络传输诱导延时、数据包丢失等。网络控制系统的研究目前也有大量的文献发表,见文献[10-15],但大多是针对一维被控对象给出的。网络约束条件下二维系统的分析和设计目前仅有少量文献发表,见文献[16-17],且主要研究数据包丢失的影响。文献[16]研究了二维Fornasini-Marchesini系统存在测量数据丢失时的鲁棒H∞滤波问题,文献[17]研究了二维Roesser系统存在数据丢失时的H∞控制器设计问题。然而,文献[16-17]针对网络二维系统的研究均假设数据在传输过程中精度是无限大的,未考虑数据量化的影响。
实际网络控制系统中,由于传输信道容量以及传感或执行设备的精确度限制,系统数据在传输前首先被量化处理。因此,数据量化是影响网络系统控制性能的一个重要因素。实事上,针对非网络控制模式下一维系统的量化控制问题已经被广泛研究。文献[18]研究了线性系统输出数据量化的稳定性问题,文献[19]研究了线性、非线性系统控制输入数据量化的稳定性问题。文献[20]提出了一种处理量化误差的扇形界方法,并基于该方法研究了线性系统的输出量化、输入量化以及状态量化问题。针对网络模式下的一维系统,文献[21]研究了系统存在状态和输入量化的保成本控制,文献[22]研究了线性时变系统的H∞量化反馈控制,文献[23]研究了线性系统的输出反馈控制。然而,上述结果均是针对一维系统给出的,基于量化数据的二维系统分析和设计目前尚无研究。
本文针对存在数据丢失的二维系统,考虑基于状态量化的反馈控制器设计方法。首先将数据丢失描述成取值为0或1的随机伯努利序列,定义了随机意义下二维系统的均方稳定性。其次,采用扇形界方法处理量化数据的影响,给出一个闭环系统均方渐进稳定的充分条件,基于该条件设计了状态反馈控制器。最后,仿真结果验证了设计方法的有效性。
1 问题描述
考虑如下二维Roesser系统
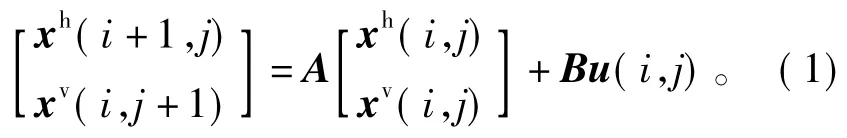
式中xh(i,j)∈Rn1,xv(i,j)∈Rn2,u(i,j)∈Rm分别表示水平状态分量、垂直状态分量以及控制输入量,A,B为系统矩阵。
假设1系统(1)的边界条件满足
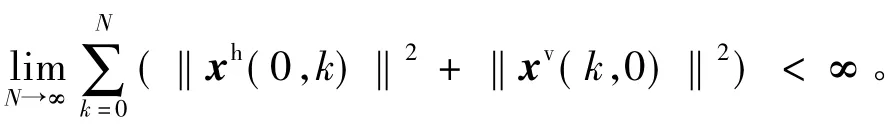
假设系统的测量信号在通过网络传输前首先进行量化处理,并采用如下逻辑量化器[24]:
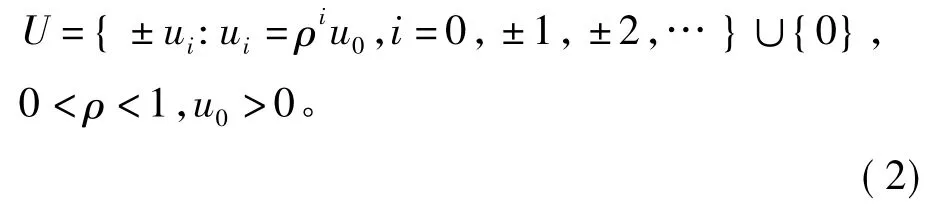
式中ρ为量化密度[24],其量化函数q(·)定义为
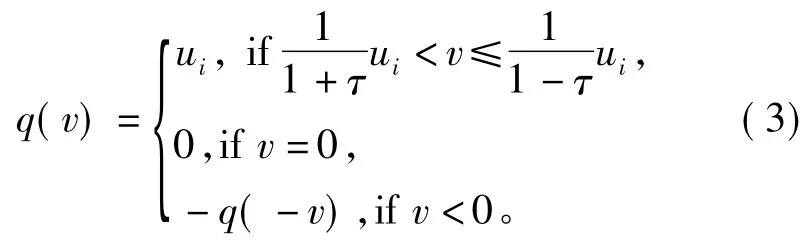
考虑如下状态反馈控制器
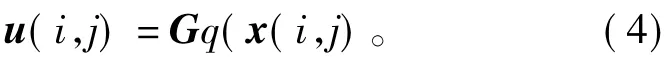
当上述控制策略通过网络控制模式实现时,状态测量的量化信号q(x(i,j)通过网络在控制器和被控对象间传输。由于网络条件的约束,使得q(x(i,j)经常产生数据包的丢失。此时,控制器(4)可被描述为
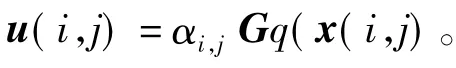
式中{αi,j}为取值0和1的随机伯努利序列,且满足
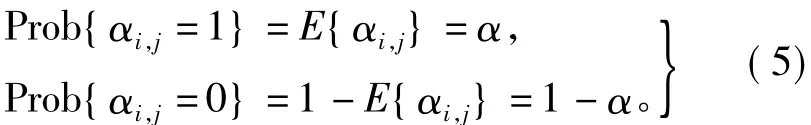
式中0≤α≤1为已知常数。
注1由于随机变量{αi,j}的引入,使得上述二维闭环系统为一个随机系统。因此,已有确定性二维系统的分析和控制器设计方法在这里无法适用。为了进行的控制器设计,我们首先给出如下二维系统的随机稳定性定义。
定义1若二维系统(1)对于零输入条件和假设1中的有界边界条件满足
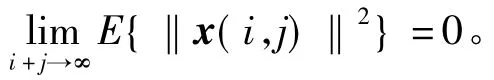
则系统均方渐进稳定。
至此,研究内容可描述为:对于满足假设1边界条件的二维系统(1),如何设计量化状态反馈控制器(4),使得系统存在数据丢失的情况下闭环二维系统均方渐进稳定。
2 主要结果
为了分析二维随机系统的稳定性,我们采用扇形界方法处理量化误差[20],即对于给定的量化密度ρ满足
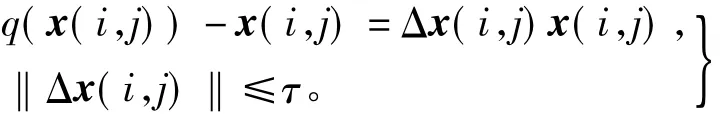
此时状态反馈控制器(4)可重写为
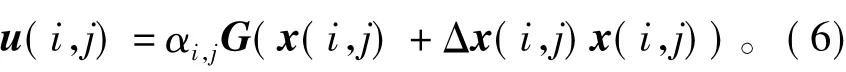
由式(1)和式(6)可得如下闭环系统表达式
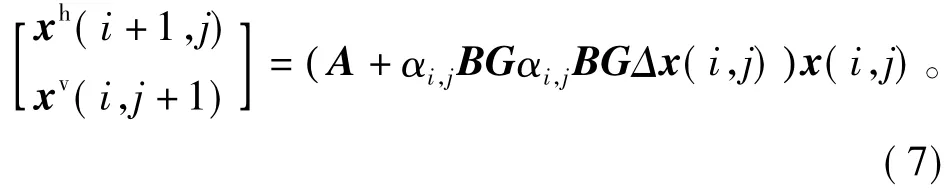
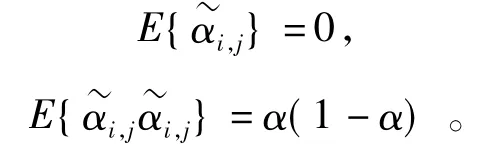
代入二维闭环系统(7)中可得
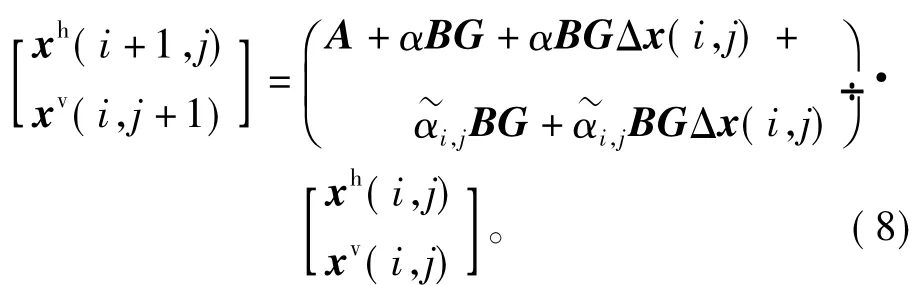
定理1若二维系统满足假设1的边界条件,当存在正定矩阵P=diag{Ph,Pv}>0满足如下条件时
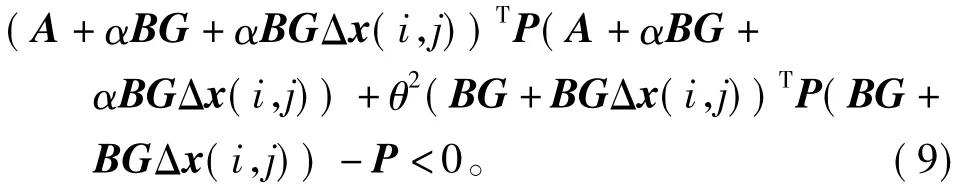
二维闭环系统(8)均方渐进稳定,式中θ2=α(1-α)。
证明定义
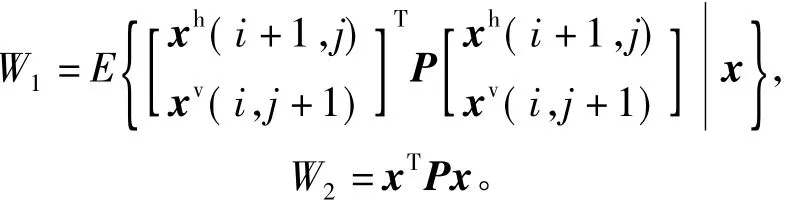
考虑如下指标
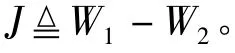
将式(8)带入上述指标可得
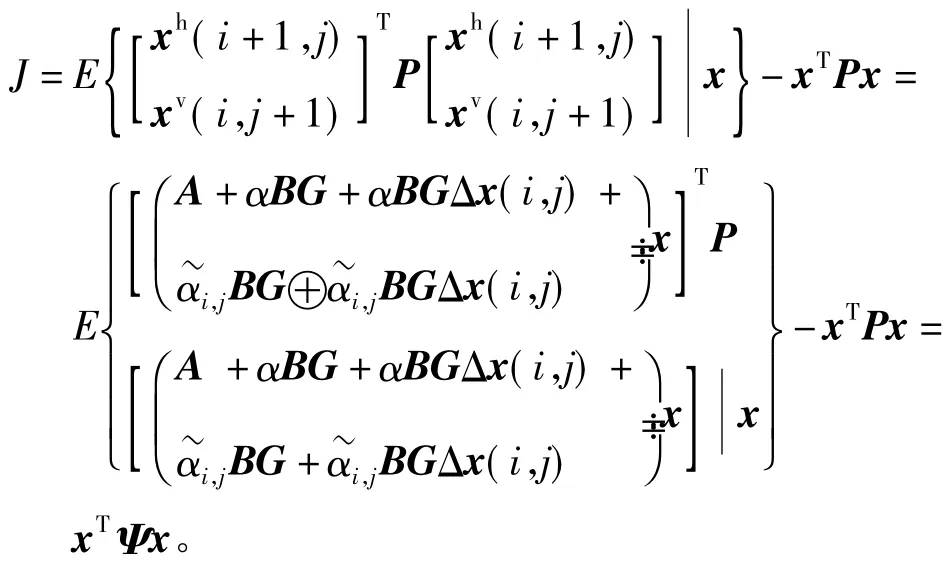
式中
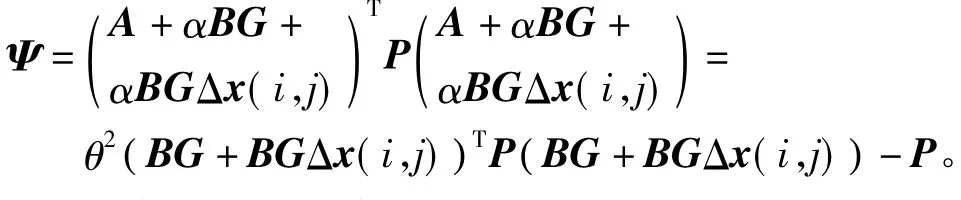
根据(9)式可知Ψ<0,因此,对于所有x≠0可得
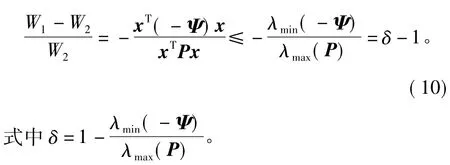
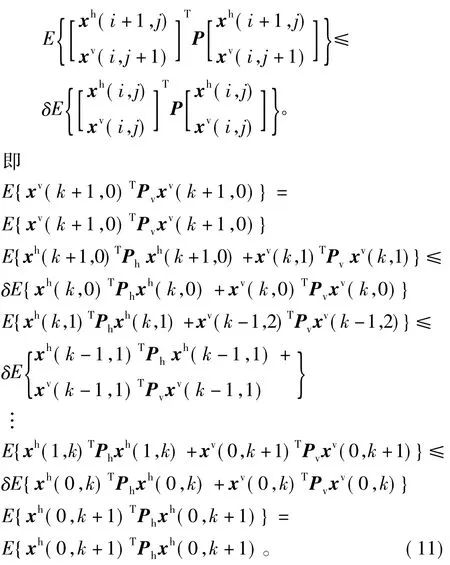
式(11)两端相加得
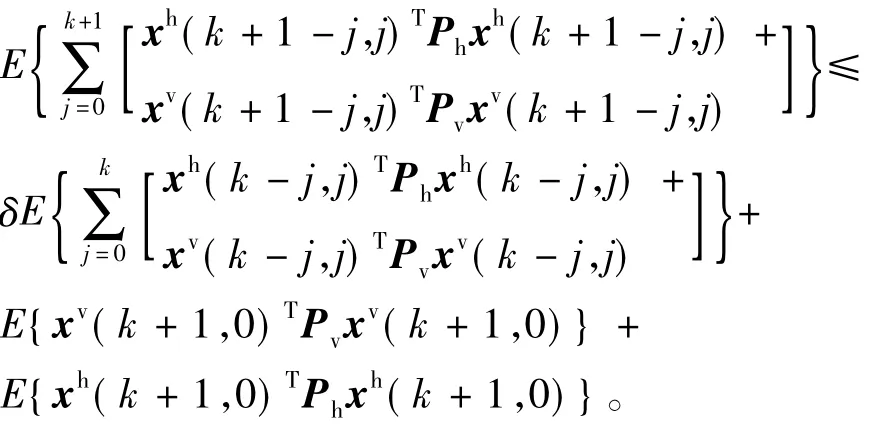
由上述关系可得
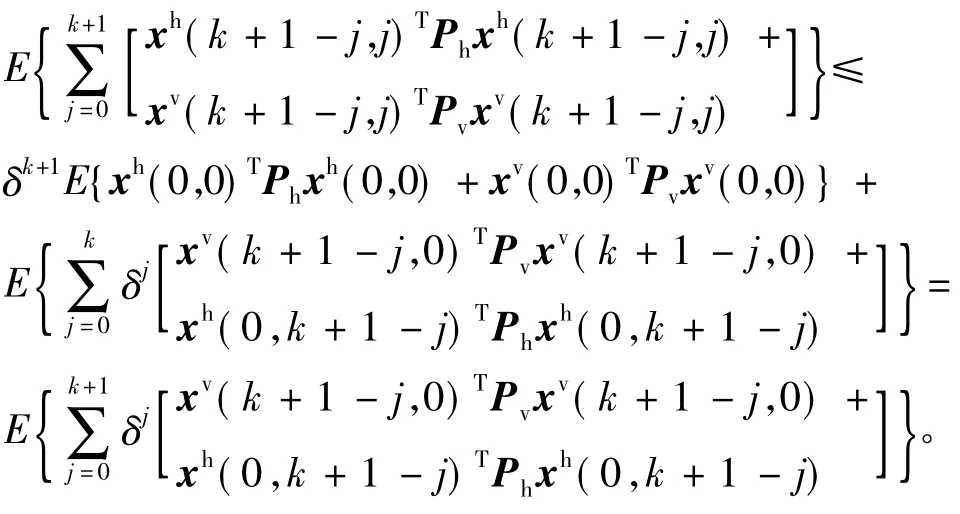
上式意味着
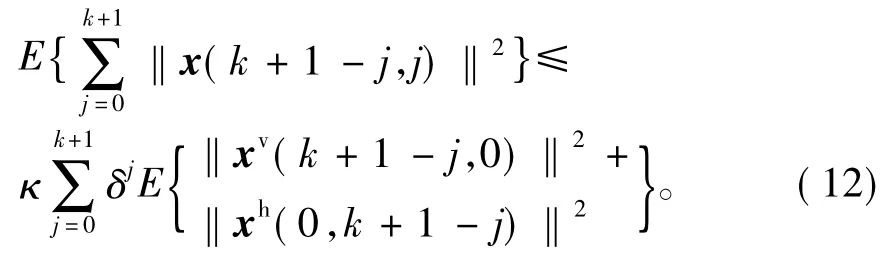
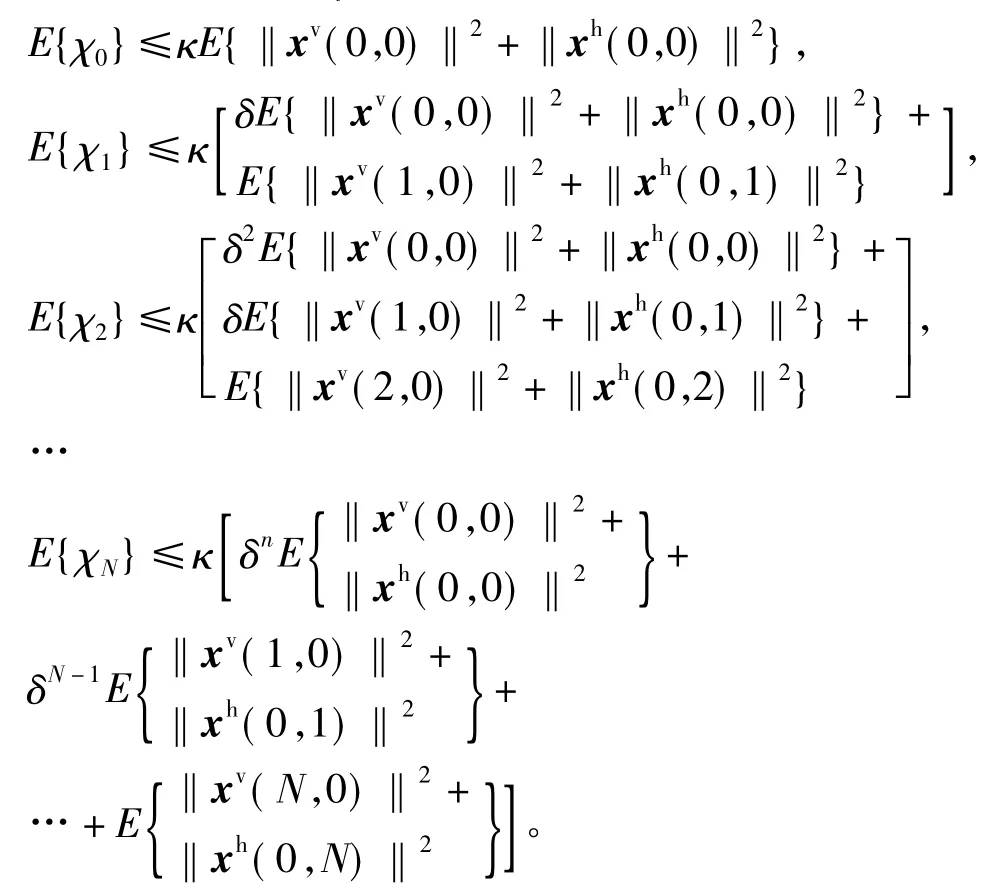
上式两端相加可得
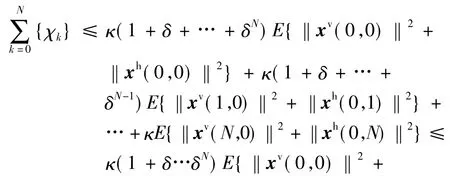
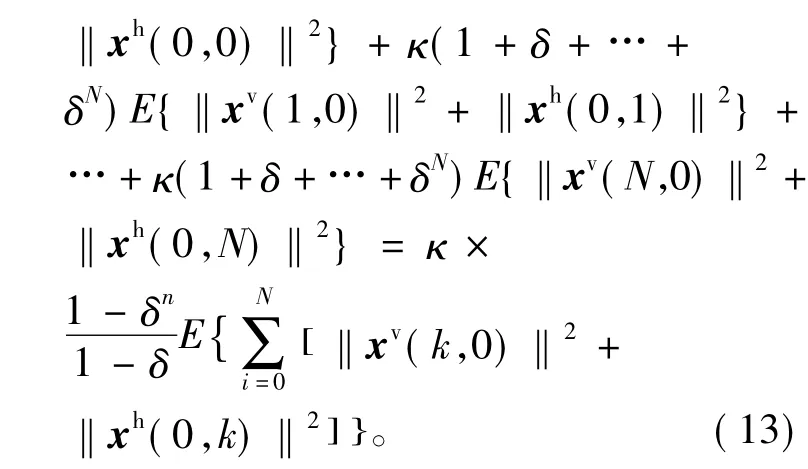
注2定理1给出了二维闭环系统均方渐进稳定的一个充分条件。当系统不存在数据丢失时,即α=1和θ=0,条件(9)变为
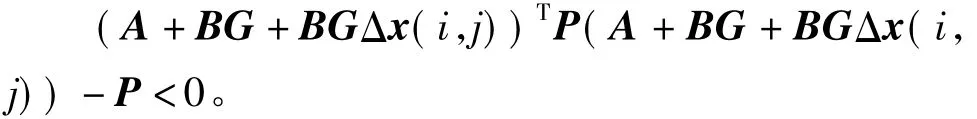
特殊的,当系统状态不存在量化误差时,即Δx(i,j)= 0,上述条件变为
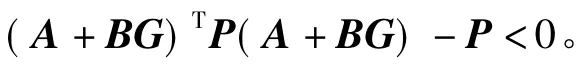
该条件为二维确定系统状态反馈控制的结果,参见文献[2]。因此,定理1的结果更具有一般意义。
定理1是在控制器G已知的情况下给出的,论文的设计目标为基于系统矩阵A,B和参数α设计G。在给出设计结果前,我们首先给出如下引理。
引理1假设X,Y为一定维数的矩阵或向量,对于任意标量ε>0和所有满足ΔΔT≤I的矩阵Δ,如下不等式成立
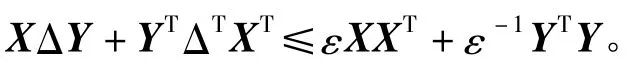
根据上述引理,我们可以给出如下结果。
定理2对于二维闭环系统(8),若存在矩阵Y,P0,正定矩阵P和标量ε>0满足
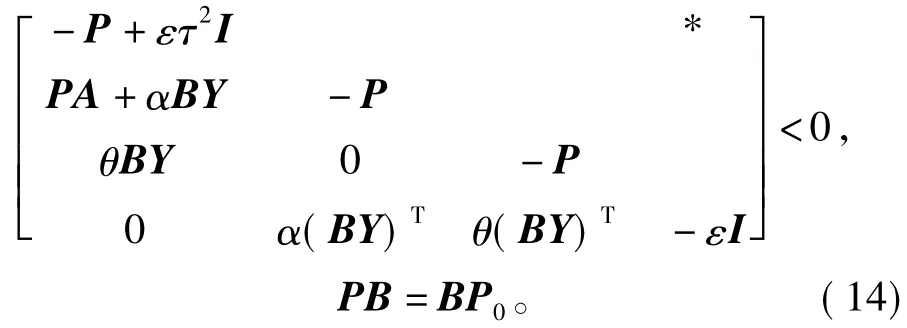
则二维闭环系统(8)均方渐进稳定。此时,状态反馈控制器(4)的增益矩阵可设计为G=P0-1Y。
证明定理1的条件可写为
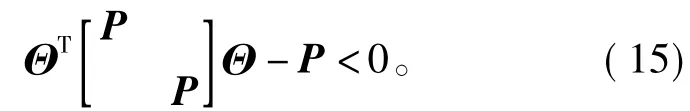
式中
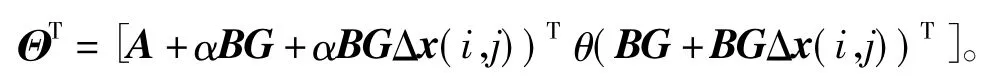
根据Schur补引理,条件(15)转化为如下不等式
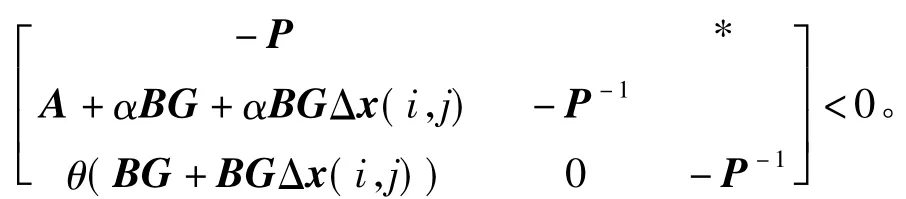
上述不等式可进一步写为
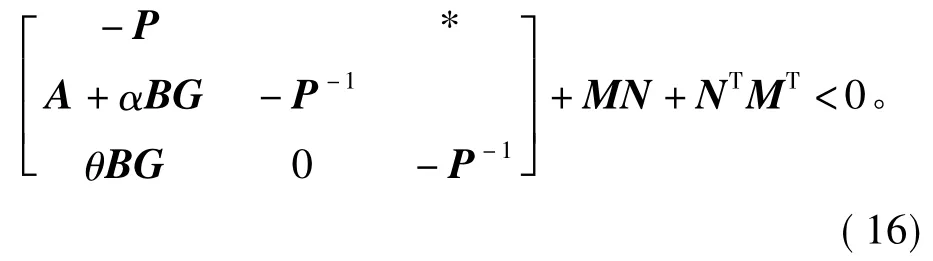
式中
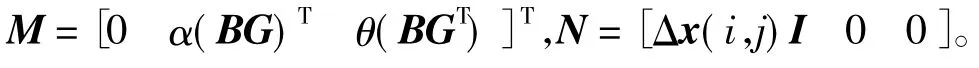
根据引理1和式(16)可知
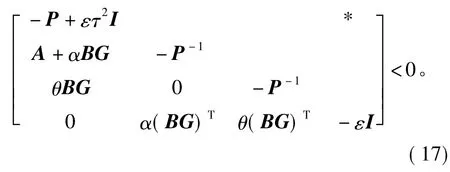
对不等式(17)分别左乘和右乘diag(I,P,P,I),并记PB=BP0,可得
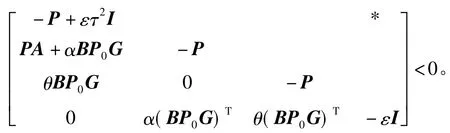
记Y=P0G可知定理2成立。
注3定理2给出了一个二维闭环系统均方渐进稳定的线性矩阵不等式条件,该条件可以通过Matlab的LMI具箱给出一个可行解,同时给出了一个满足要求的状态反馈增益矩阵。
3 仿真示例
考虑如下参数的二维系统式(1):
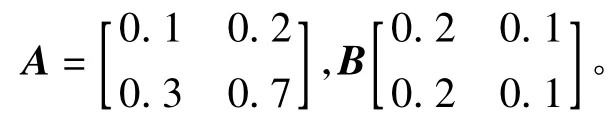
假设α=0.8,即数据经过网络传输的丢失率为20%。量化器(2)中的参数选择为u0=0.1,ρ=0.9,经计算可知该选择使得量化等级覆盖了系统状态变量的所有取值。根据定理2,将上式参数代入不等式(14)中,通过Matlab的LMI工具箱求解出如下结果

因此,反馈增益可选择为

为了验证设计的有效性,我们通过Matlab软件进行数值仿真。假设系统初始条件为
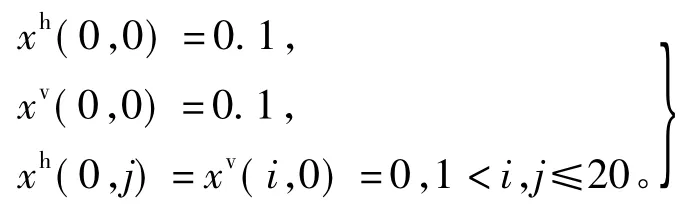
仿真结果如图1和图2所示。图1给出了xh(i,j)的状态响应轨迹,图2给出了xv(i,j)的状态响应轨迹,仿真结果表明二维系统是稳定的。因此,所提方法针对量化误差和数据丢失的二维状态反馈控制器设计是有效的。
4 结论
本文给出了一种存在数据丢失时的二维系统量化状态反馈控制器设计方法。定义了二维随机系统的均方稳定性,基于线性矩阵不等式给出了一个闭环系统稳定的充分条件,并基于该条件设计了控制器,数值仿真结果验证了设计方法的有效性。本文是在随机系统定义下进行二维系统状态控制器设计的,在此框架下也可以进行其他随机因素的二维系统分析和设计。
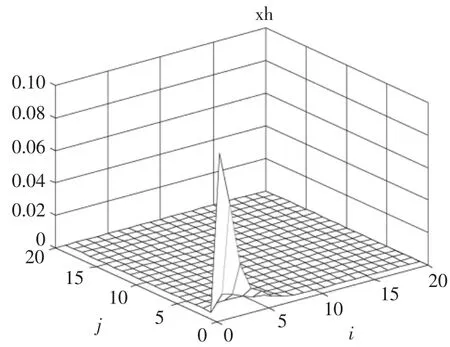
图1 状态响应xh(i,j)Fig.1 State response of xh(i,j)
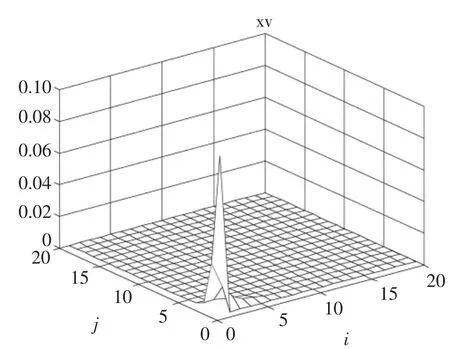
图2 状态响应xv(i,j)Fig.2 State response of xv(i,j)
[1]KACZOREK T.Two-dimensional linear systems[M].Berlin:Springer-Verlag,1985:1-43.
[2]DU Chunling,XIE Lihua.H∞control and filtering of two-dimensional systems[M].Berlin:Springer,2002:100-114.
[3]BORS D,WALCAZK S.Application of 2-D systems to investigation of a process of gas filtration[J].Multidimens.Syst.Signal Process,2012,23(1-2):119-130.
[4]SINGH V.Stability analysis of 2-D discrete systems described by the Fornasini-Marchesini second model with state saturation[J]. IEEE Transactions on Circuits and Systems II:Express Briefs,2008,55(8):793-796.
[5]DU Chunling,XIE Lihua,ZHANG Cishen.H∞control and robust stabilization of two-dimensional systems in Roesser models [J].Automatica,2001,37(2):205-211.
[6]GUAN Xinping,LONG Chengnian,DUAN Guangren.Robust optimal guaranteed cost control for 2-D discrete systems[J].IEE Proceedings on Control Theory and Applications,2001,148(5):355-361.
[7]吴敏,陈诗桓,佘锦华,等.基于二维混合模型的改进型重复控制系统保性能设计方法[J].自动化学报,2009,35(1):54 -64 WU Ming,CHEN Shihuan,SHE Jinhua,et al.Guaranteed cost design of modified repetitive control systems based on 2-D hybrid model[J].Acta Automatica Sinica,2009,35(1):54-64.
[8]WU Ligang,GAO Huijun.Sliding mode control of two-dimensional systems in roesser model[J].IET Control Theory&Applications,2008,2(4):352-364.
[9]CUI Jiarui,HU Guangda.State estimation of 2-D stochastic systems represented by FM-II model[J].Acta Automatica Sinica,2010,36(5):755-761.
[10]HESPANHA J P,NAGHSHTABRIZI P,XU Yonggang.A survey of recent results in networked control systems[J].Proceedings of the IEEE,2007,95(1):138-162.
[11]ZHANG Wei,BRANICKY M S,PHILLIPS S M.Stability of networked control systems[J].IEEE Control Systems magazine,2001,21(1):85-99.
[12]党向东,张庆灵.时变时延网络控制系统稳定性分析[J].电机与控制学报,2009,13(4):592-602. DANG Xiangdong,ZHANG Qingling.Stability analysis of NCS with time-varying delay[J].2009,13(4):592-602.
[13]WANG Zidong,YANG Fuwen,HO D W C,et al.Robust H∞control for networked systems with random packet losses[J]. IEEE Trans.Systems,Man and Cybernetics-Part B,2007,37 (4):916-924.
[14]王常虹,奚伯齐,李清华,等.网络化控制系统鲁棒L2-L∞控制器设计[J].电机与控制学报,2010,14(2):25-30. WANG Changhong,XI Boqi,LI Qinghua,et al.Robust L2-L∞controller design for networked control systems[J].Electric Machines and Control,2010,14(2):25-30.
[15]游科友,谢立华.网络控制系统的最新研究综述[J].自动化学报,2013,39(2):101-118. YOU Keyou,XIE Lihua.Survey of recent progress in networked control systems[J].Acta Automatica Sinica,2013,39(2):101-118.
[16]LIU Xiuming,GAO Huijun,SHI Peng,et al.Robust H∞filtering for 2-D systems with intermittent measurements[J].Circuits.Systems&Signal Processing.2009,28(2):283-303.
[17]BU Xuhui,WANG Hongqi,ZHENG Zheng,et al.H∞control for network-based 2-D systems with missing measurements[J]. Abstract and Applied Analysis,2014,2014(5):1-11.
[18]BROCKETT R W,LIBERZON D.Quantized feedback stabilization of linear systems[J].IEEE Transactions on Automatic Control,2000,45(7):1279-1289.
[19]LIBERZON D.Hybrid feedback stabilization of systems with quantized signals[J].Automatica,2003,39(9):1543 -1554.
[20]Fu Minyue,XIE Lihua.The sector bound approach to quantized feedback control[J].IEEE Transactions on Automatic Control,2005,50(11):1698-1710.
[21]YUE Dong,PENG Chen,TANG Gongyou.Guaranteed cost control of linear systems over networks with state and input quantizations[J].IEE Proceedings:Control Theory and Applications,2006,153(6):658-664
[22]PENG Chen,TIAN Yuchu.Networked H∞control of linear systems with state quantization[J].Information Sciences,2007,177(24):5763-5774.
[23]TIAN Engang,YUE Dong,PENG Chen.Quantized output feedback control for networked control systems[J].Information Sciences,2008,178(12):2734-2749.
[24]ELIA N,MITTER K.Stabilization of linear systems with limited information[J].IEEE Transactions on Automatic Control,2001,46(9):1384-1400.
(编辑:贾志超)
Quantized state feedback control for 2-D Roesser systems with packet dropouts
BU Xu-hui, CHENG Zi-hao, YU Fa-shan, YANG Jun-qi
(School of Electrical Engineering&Automation,Henan Polytechnic University,Jiaozuo 454000,China)
The problem of quantized state feedback control was investigated for 2-D Roesser systems with packet dropouts.It is assumed that the 2-D system is implemented via a networked control system and the states of the controlled system are available.The measurements of state signal are quantized by logarithmic quantizer before being communicated.Moreover,the measurements missing often occur due to the communication channel failure.Firstly,the data missing phenomena was modeled by a Bernoulli distributed stochastic variable taking values of 1 and 0,and the stochastic stability for the 2-D system is defined. Then,a sufficient condition was derived in virtue of the method of sector-bounded uncertainties,which guarantees that the closed-loop system was stochastically stable.Based on the condition,quantized state feedback controller was designed by using linear matrix inequalities technique.Finally,the simulation example was given to illustrate the proposed method.
2-Dsystems;networkedcontrolsystems;quantizedcontrol;missingmeasurements;stochastic system
10.15938/j.emc.2016.03.015
TP 273
A
1007-449X(2016)03-0096-06
2014-11-27
国家自然科学基金(61203065,61573129);河南省高等学校青年骨干教师资助计划项目(2014GGJS-041);河南省高等学校基本科研业务费基金项目
卜旭辉(1981—),男,博士,副教授,研究方向为迭代学习控制、网络控制以及智能交通;
程子豪(1990—),男,硕士研究生,研究方向为二维系统控制、网络控制;
余发山(1952—),男,教授,博士生导师,研究方向为工业过程控制、电力电子传动;
杨俊起(1979—),男,博士,副教授,研究方向为故障诊断、状态估计理论。
卜旭辉
