改进定子磁链估计器及其参数选取

邢岩， 王旭， 杨丹， 张志美

（1.通化师范学院计算机学院，吉林通化134000；2.东北大学信息科学与工程学院，辽宁沈阳110819）

改进定子磁链估计器及其参数选取

邢岩1， 王旭2， 杨丹2， 张志美2

（1.通化师范学院计算机学院，吉林通化134000；2.东北大学信息科学与工程学院，辽宁沈阳110819）

在永磁同步电动机直接转矩控制系统中根据电磁转矩和定子磁链误差选择合适的定子电压矢量，因此必须对定子磁链进行估计。针对传统定子磁链计算中存在的受定子电阻和反电动势积分影响等问题，研究了扩展卡尔曼滤波在永磁同步电动机定子磁链估计中的应用。建立了以定子电流，转子速度和转子位置为状态变量的扩展卡尔曼滤波估计器，进而利用永磁同步电动机的电流模型计算定子磁链。同时，在大量仿真实验基础上，总结协方差矩阵参数对系统性能的影响。实验结果表明所提出的算法不仅能准确估计速度、转子位置和定子磁链，并且对电机参数具有很强的鲁棒性。

永磁同步电机；无传感器控制；扩展卡尔曼滤波；直接转矩控制；EKF协方差矩阵参数选取DOI：10.15938/j.emc.2016.03.005

0　引言

永磁同步电机结构简单，可靠性高，功率密度高，效率高，已越来越多地应用于各种高性能要求的场合，发展前景广阔［1］。矢量控制曾经是交流电机转速和转矩控制的工业标准，1986年感应电机直接转矩控制方法的提出［2］，使直接转矩控制作为交流电机控制的另一种策略得到广泛应用，并且应用到永磁同步电机中［3］。

直接转矩控制实行定子磁场定向，避免了复杂的坐标变换，动态性能好，实现内部转矩闭环时不需要转子位置信息，因而受到越来越多的关注［4］。但是它也存缺点和限制：1）定子磁链的计算受定子电阻Rs和反电动势积分的影响；2）需要位置传感器来检测初始转子位置。

直接转矩控制的基本原理是根据估算的电磁转矩Te、定子磁链幅值|ψs|和定子磁链角度θs来选择合适的定子电压矢量，从而调节转矩和磁链值。其中：

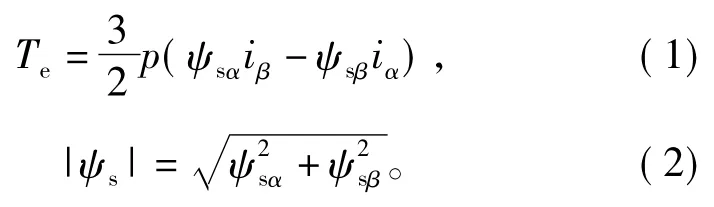
式中：p是极对数，iα、iβ分别是定子电流α轴、β轴分量，ψsα、ψsβ分别是定子磁链α轴、β轴分量。显然Te、|ψs|、θs都由ψsα和ψsβ决定，因此要想准确控制电机，定子磁链的估计至关重要。理论上，定子磁链矢量可以通过反电动势积分得到

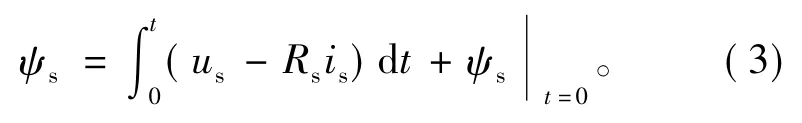
式中：ψs|t=0是t=0时刻定子磁链的初始值，Rs、us、is分别为定子电阻、电压、电流。

由于存在开环积分，us、is的直流测量偏移将导致定子磁链计算误差大，而且在电机运行过程中Rs随温度的升高而增加，也会导致定子磁链计算不准确，因此许多文献中提出改进的磁链估计方法。包括对直流测量偏移进行补偿［5］，这种方法以直流偏移量常数为前提，但这在实际运行中并不满足；利用可编程低通滤波器对定子磁链进行估计［6］；利用PI控制器跟踪定子电阻［7］；使用永磁同步电机的电流模型［8］，这两种方法需要用到转子位置信息，导致系统中增加位置传感器。这些方法都增加了计算量和系统模型的复杂度。

本文将扩展卡尔曼滤波应用到直接转矩控制中，利用永磁同步电机电流模型计算定子磁链，同时将速度和转子位置作为滤波器状态分量进行估计。并详细阐述EKF协方差矩阵参数对PMSM控制系统性能的影响，给出协方差矩阵参数的选取规律。

1　直接转矩控制及其模型

在永磁同步电机DTC系统中，建立以定子磁链误差信号、电磁转矩误差信号和定子磁链所处的扇区号为输入，以空间电压矢量为输出的矢量开关表，如表1所示，根据转矩和磁链误差选择合适的定子电压矢量。直接转矩控制只用到定子电阻值，不需要电流控制器和其他电机参数，因此和矢量控制相比，直接转矩控制具有参数依赖少、转矩响应快等优点。图1给出了直接转矩DTC开关矢量图。

表1　选择空间电压矢量的逆变器开关表Table 1　Inverter switch table with space voltage vectors

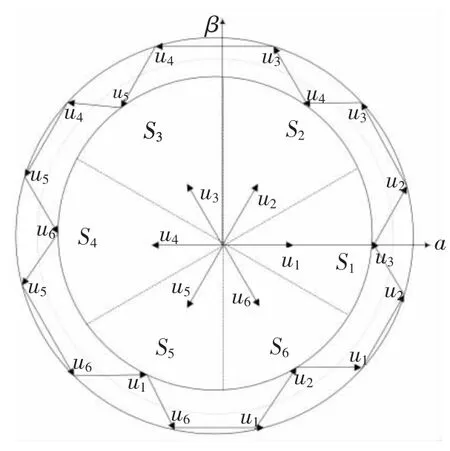
图1　DTC开关矢量Fig.1　Switching vectors for DTC

2　基于EKF的定子磁链估计

理论上定子磁链可由式（3）对反电动势积分得到，但存在偏移，因此采用SPMSM在两相静止坐标系（α，β）的电流模型计算定子磁链：

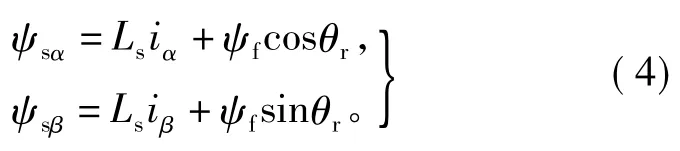
式中：Ls是同步电感，ψf是永磁磁链，θr是转子位置电角度。

直接转矩控制不需要从静止坐标系到旋转坐标系的转换，因此本质上是一种无传感器控制策略，而由式（4）可以看出，计算定子磁链需要用到转子位置信息是一个主要缺点。为了估计转子位置信息，需要使用状态观测器，经过仔细研究，选用扩展卡尔曼滤波方法，将 iα、iβ、θr作为状态变量同时进行估计。

2.1卡尔曼滤波原理

卡尔曼滤波是一种最小方差意义上的最优预测估计，采用状态空间法在时域内设计滤波器，用状态方程描述任何复杂的多维信号的动力学特性，设计简单易行［9］。对于非线性系统可以采用扩展卡尔曼滤波，利用系统动态模型、可测量状态（如定子电压、电流）和系统及量测噪声对不可测状态（如转速、转子位置）进行估计。卡尔曼滤波算法分为两个阶段：预测阶段和修正阶段，如图2所示。预测阶段：由测得的输入量uk和电机模型f（xk，uk）得到电机下一个状态向量的估计值，由此计算出下一个状态输出向量的估计值并与实际测得的输出向量值zk+1进行比较。修正阶段：利用上一步所得误差、测量噪声协方差矩阵R、系统噪声协方差矩阵Q对状态值进行修正，同时计算卡尔曼增益矩阵Kk+1。

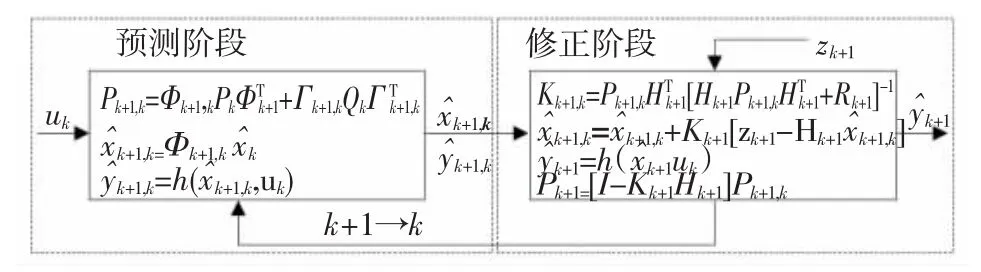
图2　卡尔曼滤波算法方框Fig.2　Block diagram of Kalman Filter

2.2扩展卡尔曼滤波及滤波公式

假设转动惯量无穷大，即忽略运动方程，由于转速ωr包含在状态向量中，所以选取合适的协方差矩阵，EKF可以纠正这个模型误差。选取x=［iαiβωrθr］T为状态变量，u=［uαuβ］T为输入变量，y=［iαiβ］T为输出变量。永磁同步电机控制系统状态方程和观测方程如式（5）所示：

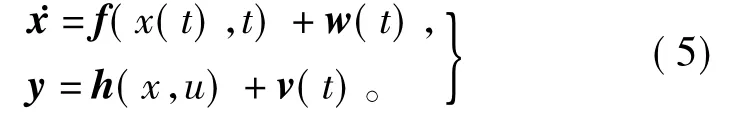
式中，w（t）是系统随机噪声，v（t）量测噪声，协方差矩阵分别为Q，R，两者均为零均值高斯白噪声且互不相关；

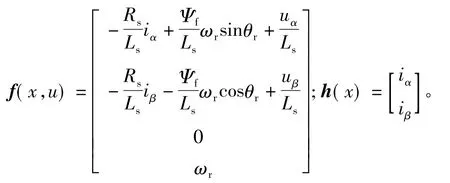
则相应的卡尔曼基本滤波公式为：

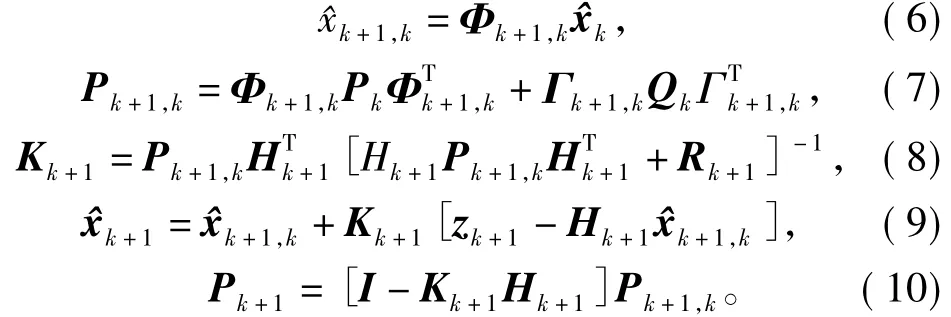
2.3定子电阻变化的影响

本节讨论传统DTC中定子电阻变化对定子磁链和电磁转矩估计的影响，以及引入EKF后对其改善效果，仿真用的PMSM参数见表2。

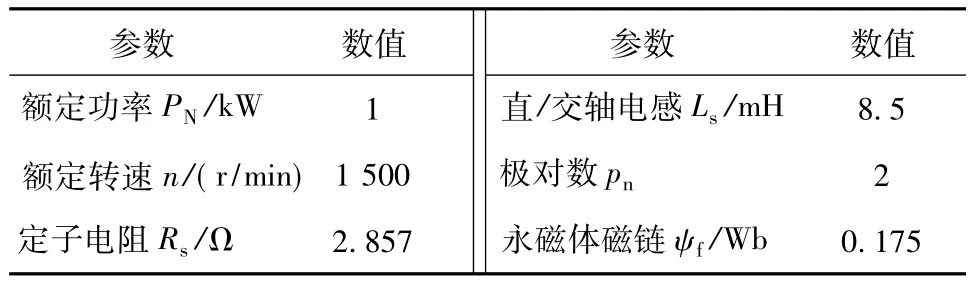
表2　永磁同步电机的参数Table 2　Parameters of PMSM

在传统直接转矩控制中，由于采用式（3）估计定子磁链，因此定子电阻变化将导致定子磁链估计误差，尤其是在低速的时候。低速时，定子电阻压降相对较大，甚至接近于反电动势，如果实际定子电阻值发生变化，而和估计式（3）中使用的值不一致时，就会在ψs、Te的参考值与实际值之间产生较大的误差，在低转速高负载的情况下还会引起系统不稳定。EKF估计器可以很好的处理定子电阻误差，因为f（x，u）中含有Rs，整个控制系统对Rs形成闭环，当Rs变化时，EKF估计器可以通过闭环结构修正模型误差，改善定子电阻存在误差时的系统性能。引入EKF后（DTC_EKF）的系统结构框图如图3所示。

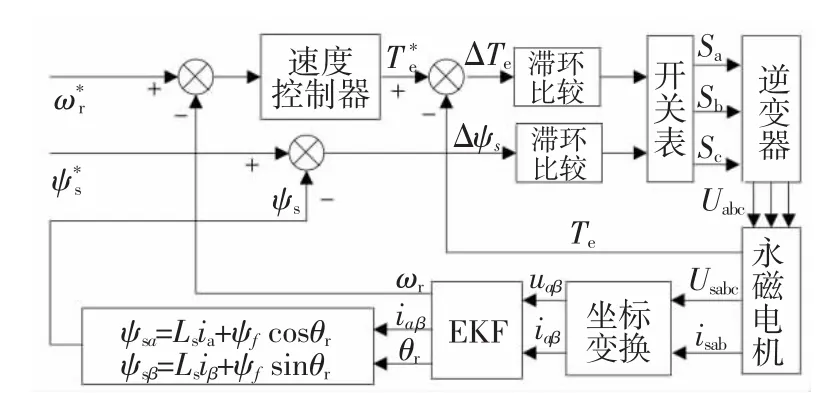
图3　DTC-EKF原理Fig.3　Block diagram of DTC_EKF

为便于比较，图4中给出了DTC-EKF系统的磁链幅值波形（图a）和传统DTC系统的定子磁链幅值波形（图b）。仿真条件：参考速度为1 000 r/min，参考定子磁链为0.2Wb，初始状态为零状态。可以看出，图（a）中磁链幅值波形宽度（约为0.008Wb）明显小于图（b）中磁链幅值波形宽度（约为0.02Wb），说明与传统直接转矩控制中采用的反电势积分法相比，基于扩展卡尔曼滤波算法估计的定子磁链脉动有很大程度的降低。

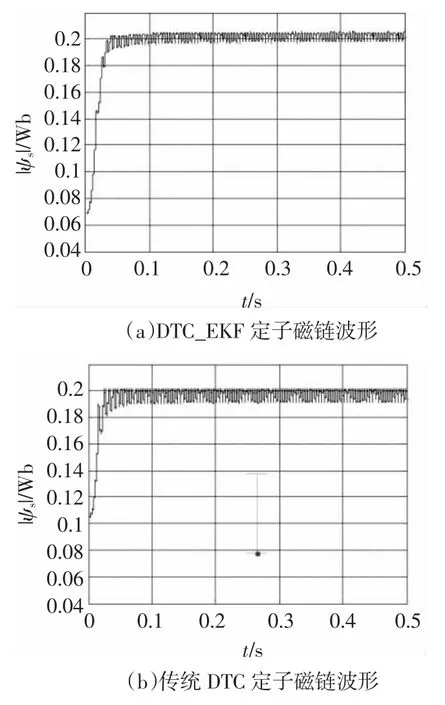
图4　定子磁链幅值波形Fig.4　Waveform of stator flux linkage amplitude

电机在运行过程中会产生一定温升，定子电阻值Rs随温度变化而发生变化，图5和图6分别给出Rs=4.653时传统DTC和DTC-EKF的仿真波形，参考速度为1 000 r/min，负载转矩为1N·m。

可以看出，估计定子磁链偏离给定轨迹，磁链α轴和β轴分量均非正弦，如果实际定子电阻值大于估计式中使用的电阻值，那么，估计的转矩大于实际转矩，反之亦然。

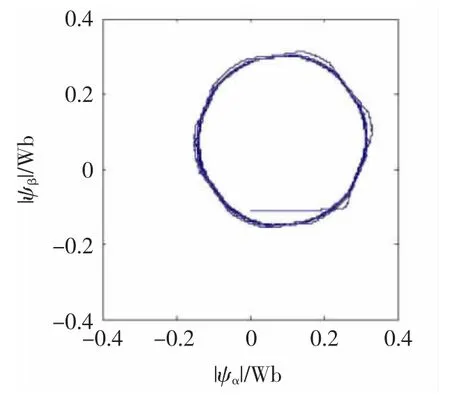
图5　Rs=4.653时传统DTC波形Fig.5　Conventional DTC waveform when Rs=4.653

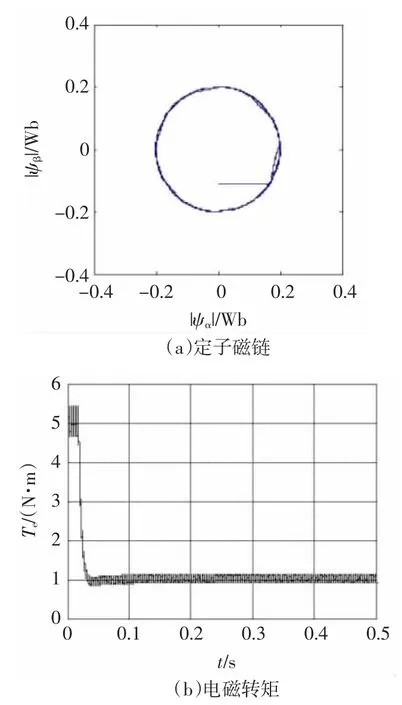
图6　Rs=4.653时EKF-DTC波形Fig.6　EKF-DTC waveform when Rs=4.653

采用电流模型和EKF后由于形成闭环结构，在实际定子电阻增大时，可以很好的处理实际阻值与估计式中使用的阻值之间的误差，估计得到的定子磁链、转矩值与实际值相等，且磁链和转矩脉动小。

3　协方差矩阵Q和R的选取

在EKF中协方差矩阵P0、Q和R的选择影响到系统的性能和稳定性，是EKF设计中的关键，本节详细给出了协方差矩阵参数的选取规律及其对系统响应的影响。

初始状态协方差矩阵P0表示初始条件的方差或均方误差，P0中参数改变会影响瞬时值，但不会影响响应时间和稳态值［10］。Q表示系统的统计描述，增加Q中的参数表明系统噪声或系统参数的不确定性增加，同时Q增加导致滤波增益K增加，加快系统响应速度。反之，滤波增益K减小，系统响应速度慢。R表示量测噪声，增加R中的参数表明量测噪声大，测量值在滤波估计中所占比例减小。

由于没有充足的统计信息来选择非对角线上的参数，通常假设P0、Q和R均为对角矩阵［11］。而且，实践表明即使非对角线上的参数初始值选为非零，当系统达到稳态时非对角线上参数值要比相应对角线上参数值小若干倍［12］。

通常选取

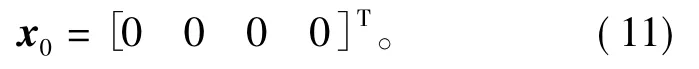
正如前面描述的，P0的初始值对EKF估计性能影响很小，在后面的实验过程中取

由于忽略机械方程，EKF估计速度总是滞后于实际速度，滞后的时间依赖于协方差矩阵Q的参数。首先采用开环结构（速度反馈使用测量值），在不改变PI控制器参数的情况下，得到协方差矩阵Q参数变化对响应的影响。图7给出开环控制情况下，不同Q11=Q22值的阶跃速度响应，其中Q33=500、Q44=0.1固定，由于篇幅限制图中只给出三种情况，当Q11= Q22值小于3时，滞后时间改变很小，而且值过小带来超调。图8给出开环控制情况下，不同Q33值的阶跃速度响应，其中Q11=Q22=3、Q44=0.1固定。图9给出开环控制情况下，不同Q44值的阶跃速度响应，其中Q11=Q22=3、Q33=500固定。

为了进一步研究协方差矩阵各参数对系统响应时间的影响，采用闭环结构（速度反馈使用EKF估计值），PI控制器参数和协方差矩阵参数使用和开环控制时相同的值。图10为闭环控制情况下，不同Q11= Q22值的速度响应时间曲线。图11为闭环控制情况下，不同Q33值的速度响应时间曲线。图12为闭环控制情况下，不同Q44值的速度响应时间曲线。

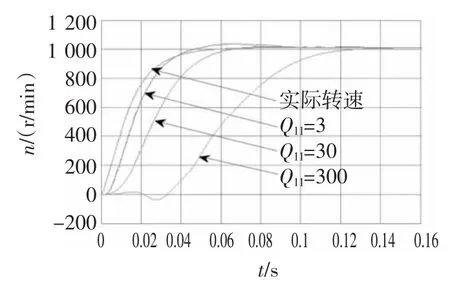
图7　不同Q11值EKF开环估计速度曲线Fig.7　Estimated speed waveform of open loop at different Q11

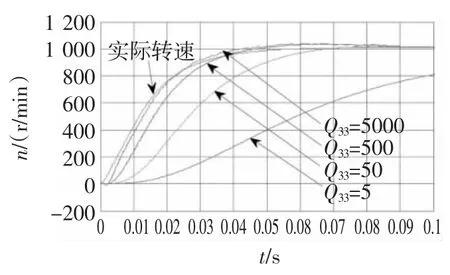
图8　不同Q33值EKF开环估计速度曲线Fig.8　Estimated speed waveform of open loop at different Q33

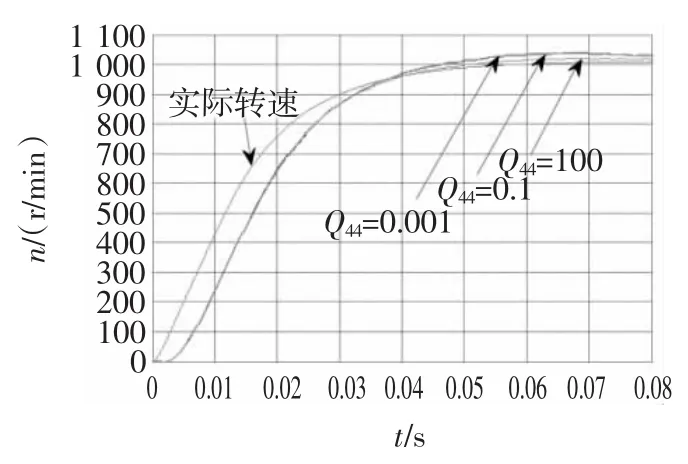
图9　不同Q44值EKF开环估计速度曲线Fig.9　Estimated speed waveform of open loop at different Q44

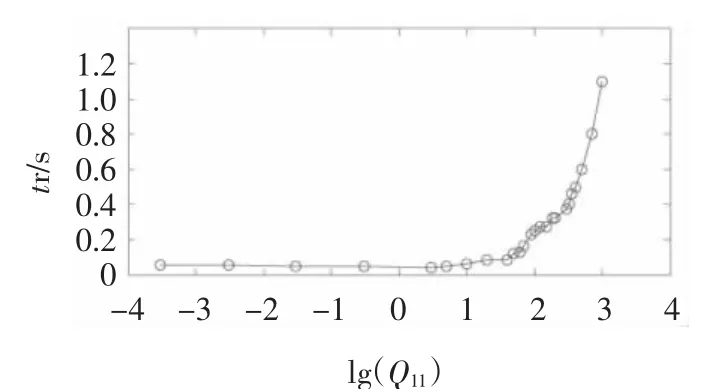
图10　不同Q11值EKF闭环估计响应时间Fig.10　Settling time of closed loop at different Q11

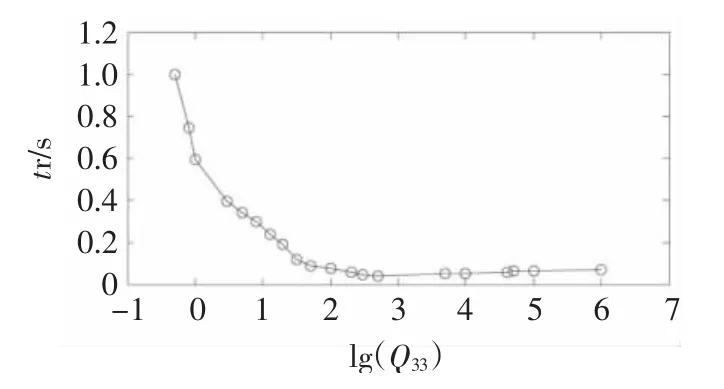
图11　不同Q33值EKF闭环估计响应时间Fig.11　Settling time of closed loop at different Q33

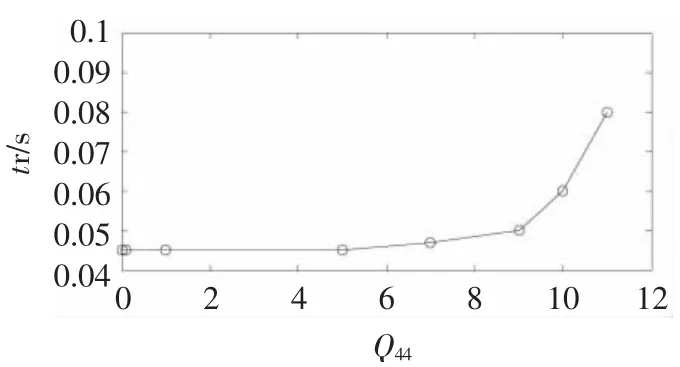
图12　不同Q44值EKF闭环估计响应时间Fig.12　Settling time of closed loop at different Q44

由图7可以看出Q11=Q22值越小，EKF估计速度滞后于实际速度的时间越短，系统响应时间越短，Q11= Q22值过大导致系统不稳定。需要注意的是 Q11= Q22小意味着电机模型的高可靠性，这在实际中很难满足，同时考虑图中估计速度波形，选定Q11=Q22=3。

Q33值越小估计速度滞后时间越长，系统响应时间越长，甚至产生波动引起系统不稳定；Q33值大不会导致系统发散，但包括强烈的噪声信号，如图8中灰色曲线（Q33=5 000）。

由图9可知，Q44值越小估计速度超调越大；Q44对EKF的收敛性影响最大，图12表明只有Q44在0 到10之间很小范围内变化时，系统稳定，且响应时间随Q44值增加而增大，Q44超过这个范围引起系统波动甚至不稳定。

协方差矩阵R与系统量测噪声有关，极高的R参数值使收敛时间增加至系统不稳定，大量的仿真实验研究表明一个可行的方法是令R=I，I为单位矩阵。

根据前面的分析结合图7至图12，取：

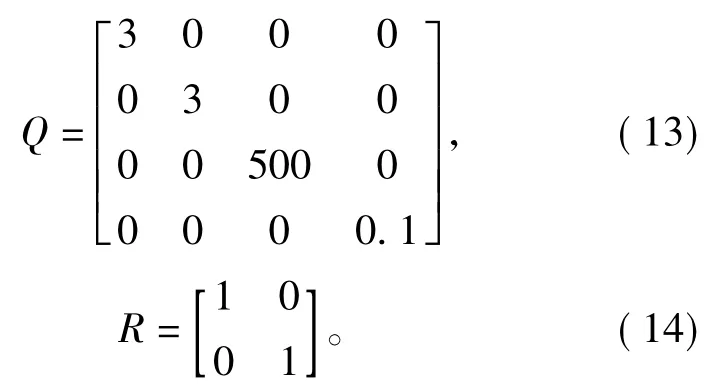
使用前面选取的初始值及协方差矩阵值估计速度和转子位置，仿真条件1：电机在空载下启动，参考速度为800 r/min，0.4 s时参考速度阶跃为1 000 r/min，仿真波形如图13所示；仿真条件2：参考速度为300 r/min，给定负载为4N·m，仿真结果如图14所示。

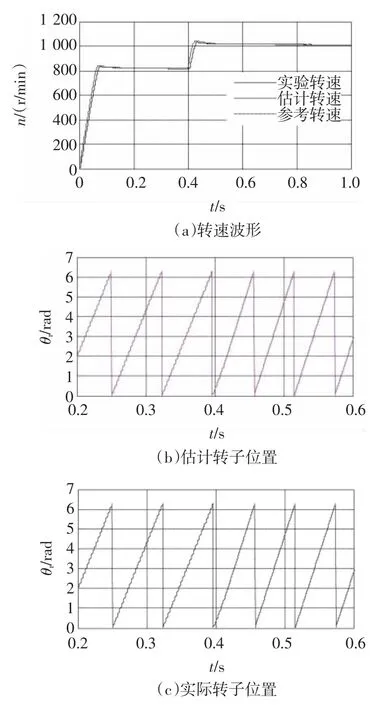
图13　空载时的速度和转子位置波形Fig.13　Speed and rotor position waveforms at no-load

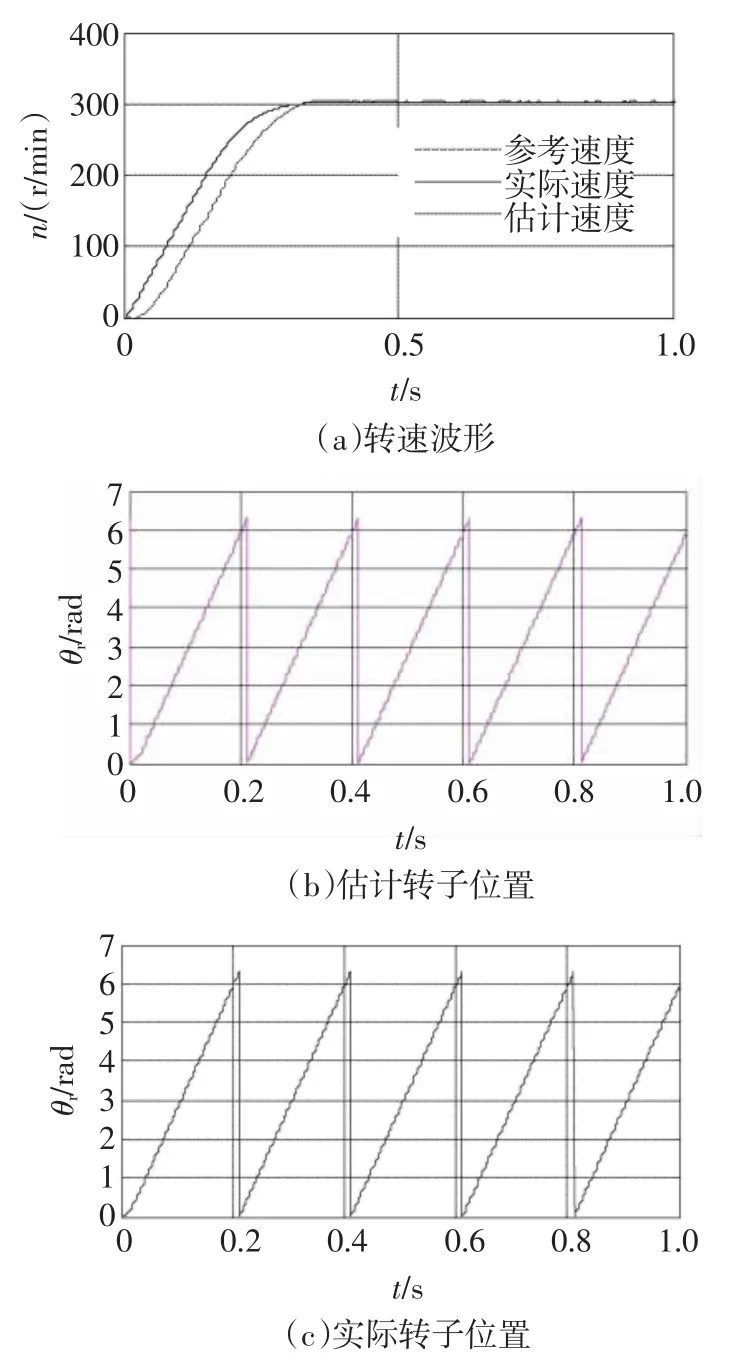
图14　重载时的速度和转子位置波形Fig.14　Speed and rotor position waveforms at heavy-load

可以看出，在两种仿真条件下EKF估计值均可以快速准确的跟踪实际值，在电机启动和参考速度突变时误差小，能快速消除误差，系统速度稳定上升。

4　实验结果

为了验证基于EKF定子磁链估计器性能，以DSP2812为控制核心，搭建实验平台，实验用4对极的隐极式永磁同步电机，额定功率为200 W，额定电压为220 V，参考速度为600 r/min，负载转矩为3 N·m，图15和图16分别给出DTC-EKF系统和传统DTC系统的实验结果。

对比图15（a）、（b）和图16（a）、（b）可知，基于EKF观测器的DTC系统定子磁链脉动降低，磁链矢量轨迹圆平滑，表现为定子磁链分量ψα和ψβ波形的正弦波曲线变细，磁链矢量圆的带宽变窄，扇区边界处的畸变明显改善。而且，基于EKF算法的估计转子位置能实时准确的跟踪实际值，估计精确度高。

实验结果验证了基于EKF算法在有效降低磁链脉动，提高系统参数鲁棒性，改善系统性能的同时，可以准确估计转速和转子位置，实现了无传感器运行。

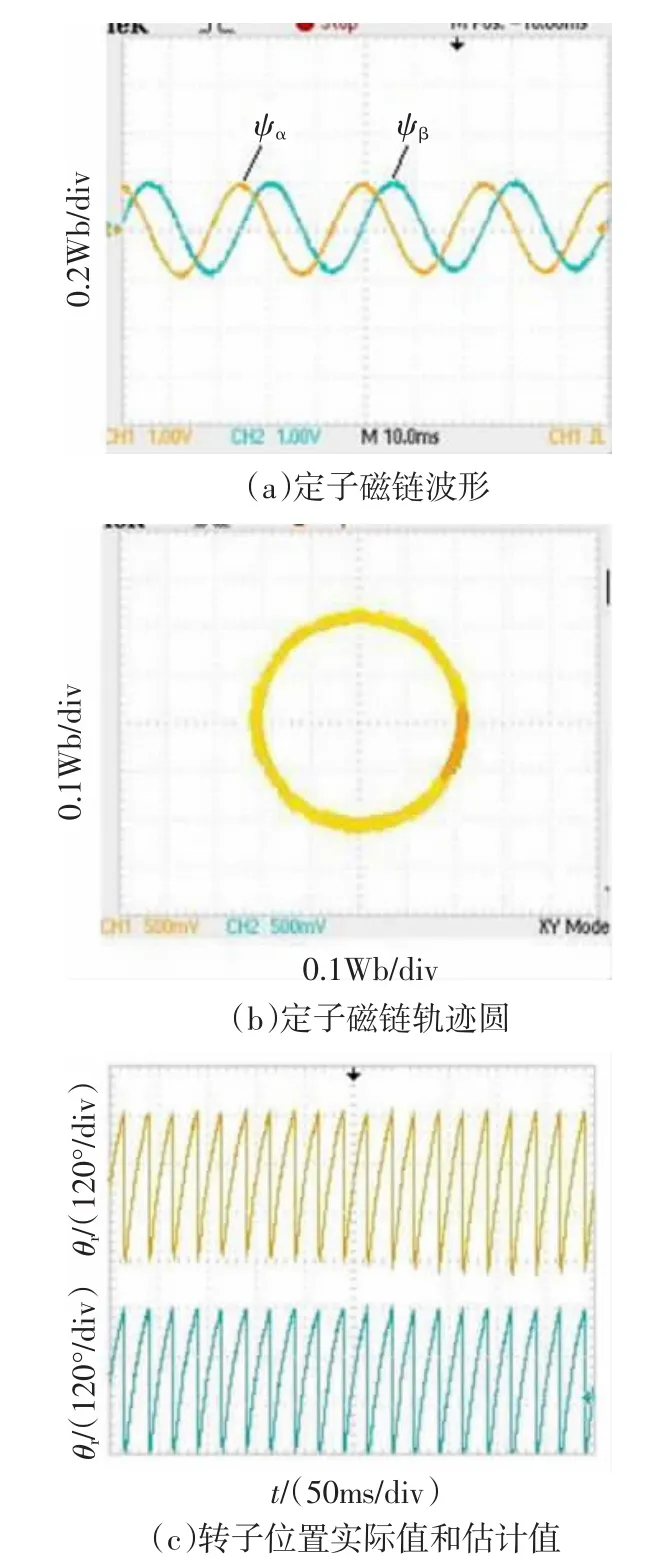
图15　EKF-DTC系统实验波形Fig.15　Experimental waveforms of EKF-DTC system

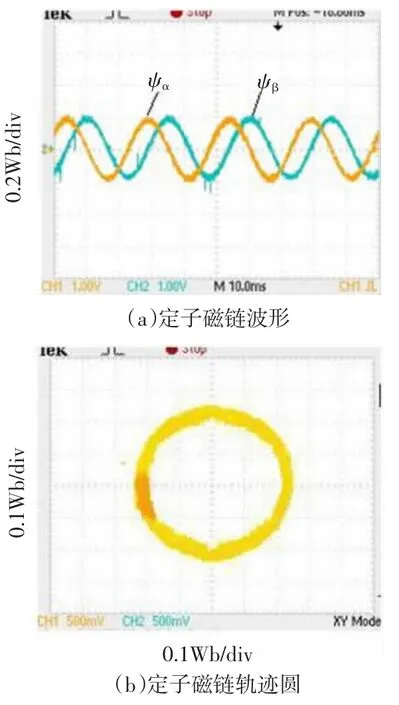
图16　传统DTC系统实验波形Fig.16　Experimental waveforms of conventional DTC system

5　结论

本文采用扩展卡尔曼滤波和永磁电机电流模型估计定子磁链，减小转矩和磁链脉动，由于扩展卡尔曼滤波函数具有滤除干扰噪声的性能，加之闭环系统本身对干扰的抑制作用，本文提出的基于EKF的定子磁链估计器解决了传统DTC中定子磁链估计受电阻影响大的问题；克服了传统DTC中纯积分法的缺陷；扩展卡尔曼滤波在估计定子磁链的同时对转子位置进行估计，不需要额外附加转子位置传感或转子位置估计器。另外，本文在大量仿真实验基础上给出EKF协方差矩阵参数的选取规律及其对系统性能的影响，实验结果表明按照本文所述规律选取参数，在速度突变的情况下，可以使EKF估计速度和转子位置快速的跟踪实际值，最终稳定在参考值，具有很好的动态和静态性能，而且无需系统机械参数，增强了系统的鲁棒性。

［1］陈振，刘向东，戴亚平，等.采用预期电压矢量调制的PMSM直接转矩控制［J］.电机与控制学报，2009，13（1）：40-46. CHEN Zhen，LIU Xiangdong，DAI Yaping，et al.Novel direct torque control of PMSM based on expected voltage space vector modulation［J］.Electric Machines and Control，2009，13（1）：40-46.

［2］TAKAHASHI I，NOGUCHI T.A new quick-response and highefficiency control strategy of an induction motor［J］.IEEE Trans on Industry Applications，1986，22（5）：820-827.

［3］田淳，胡育文.永磁同步电机直接转矩控制系统理论及控制方案的研究［J］.电工技术学报，2002，17（1）：7-11. TIAN Chun，HU Yuwen.Study of the scheme and theory of the direct torque control in permanent magnet sychronous motor drives［J］. Transactions of China Electrotechnical Society，2002，17（1）：7-11.

［4］李耀华，刘卫国.永磁同步电机直接转矩控制不合理转矩脉动［J］.电机与控制学报，2007，11（2）：148-152. LI Yaohua，LIU Weiguo.Unreasonable torque ripple of direct torque control in permanent magnet synchronous［J］.Electric Machines and Control，2007，11（2）：148-152.

［5］CHAPUIS Y A，ROYE D，DAVOINE J.Principles and implementation of direct torque control by stator flux orientation of an induction motor［C］//Applied Power Electronics Conference and Exposition，Dallas Tx USA，1995：479-483.

［6］RAHMAN M F，HAQUE M E，TANG L，et al.Problems associated with the direct torque control of an interior permanent-magnet synchronous motor drive and their remedies［J］.IEEE Trans on Industry Electronics，2004，51（4）：799-809.

［7］HAQUE M E，RAHMAN M F.Influence of stator resistance variation on direct torque controlled interior permanent magnet synchronous motor drive performance and its compensation［C］//Industry Applications Conference，Chicago IL USA，2001：719-730.

［8］ANDREESCU G D，PITIC C I，BLAABJERG F，et al.Combined flux observer with signal injection enhancement for wide speed range sensorless direct torque control of ipmsm drives［J］.IEEE Trans on Energy Conversion，2008，23（2）：393-402.

［9］尹忠刚，赵昌，钟彦儒，等.采用抗差扩展卡尔曼滤波器的感应电机转速估计方法［J］.中国电机工程学报，2012，32（18）：152 -159. YIN Zhonggang，ZHAO Chang，ZHONG Yanru，et al.A speed estimation method of induction motors using the robust extended Kalman filter［J］.Proceedings of the CSEE，2012，32（18）：152 -159.

［10］ DHAOUADI R，MOHAN N，NORUM L.Design and implementation of an extended kalman filter for the state estimation of a permanent magnet synchronous motor［J］.IEEE Trans on Power E-lectronics，1991，6（3）：491-497.

［11］BOLOGNANI S，OBOE R，ZIGLIOTTO M.Sensorless full-digital PMSM drive with EKF estimation of speed and rotor position ［J］.IEEE Trans on Industry Electronics，1999，46（1）：184 -191.

［12］BOLOGNANI S，TUBIANA L，ZIGLIOTTO M.Extended kalman filter tuning in sensorless PMSM drives［J］.IEEE Trans on Industry Applications，2003，39（6）：1741-1747.

（编辑：贾志超）

Novel stator flux linkage estimator and choice of its parameters

XING Yan1， WANG Xu2， YANG Dan2， ZHANG Zhi-mei2
（1.College of Computer，Tonghua Normal University，Tonghua 134000，China；2.College of Information Science and Engineering，Northeastern University，Shenyang 110819，China）

The change of the stator flux linkage vector depend on torque and stator flux errors，so stator flux estimation is an indispensable part of direct torque control（DTC）system of permanent magnet synchronous motor（PMSM）.Extended Kalman filter（EKF）was studied to sove problems of low robustness with stator resistance and integration of back electromotive force in conventional stator flux estimation. And EKF estimator was established by taking the stator current，rotor speed and rotor position as state variable，and then，the value of stator flux was calculated based on the current model of PMSM.Still，the effect on system performance of the EKF covariance matrices was mentioned based on lots of simulations.The results indicate that the proposed method not only do well in speed，rotor position and stator flux linkage estimation，but also has robust to motor parameters.

permanent magnet synchronous motor；sensorless control；extended Kalman filter；direct torque control；choice of the extended Kalman filter covarian ce matrices

TM 351

A

1007-449X（2016）03-0029-07

2013-04-10

中央高校基础科研项目（N100304008）

邢岩（1986—），女，博士，研究方向为永磁同步电机控制及其应用；

王旭（1956—），男，教授，博士生导师，研究方向为电机及其控制、自动化装置与智能控制系统；

杨丹（1979—），女，博士，讲师，研究方向为智能信号处理技术；

张志美（1982—），女，博士研究生，讲师，研究方向为智能信号处理技术。

邢岩