Halbach阵列同心式磁力齿轮参数分析与优化设计

井立兵， 柳霖， 章跃进， 苏建华

（1.三峡大学电气与新能源学院，湖北宜昌443002；2.湖北省微电网工程技术研究中心，湖北宜昌443002；3.上海大学机电工程与自动化学院，上海200072；4.中国电子科技集团第27研究所，河南郑州450047）

Halbach阵列同心式磁力齿轮参数分析与优化设计

井立兵1，2， 柳霖1， 章跃进3， 苏建华4

（1.三峡大学电气与新能源学院，湖北宜昌443002；2.湖北省微电网工程技术研究中心，湖北宜昌443002；3.上海大学机电工程与自动化学院，上海200072；4.中国电子科技集团第27研究所，河南郑州450047）

直驱式同心式磁力齿轮在低速大转矩领域有广泛的应用前景。为获得较正弦分布气隙磁场，所用永磁体采用Halbach阵列充磁，用二维全局解析法计算同心式磁力齿轮磁场分布；分析了调磁环铁心宽度、调磁环高度及外转子轭部厚度等参数与磁力齿轮最大静态转矩之间的关系。磁场全局解析法计算结果与有限元分析结果一致性较好，验证了解析模型的正确性；根据参数分析结果，制作了一台内转子4对极、外转子17对极的Halbach阵列同心式磁力齿轮样机，样机试验结果表明，合理选择结构参数可以提高磁力齿轮的转矩密度，对磁力齿轮的设计提供一种有益参考。

同心式磁力齿轮；Halbach阵列；全局解析法；气隙磁场；转矩密度；调磁环

0　引言

同心式磁力齿轮是利用磁场的耦合来传递动力的机械装置，与传统机械齿轮相比，同心式磁力齿轮不仅具有振动噪声小、可靠性高、运行过程中无需润滑，自动过载保护功能等优点，而且传动转矩密度能够达到100.kN·m/m3［1-2］，完全有能力与横向磁通永磁电机相媲美［3-4］。所以磁力齿轮已经越来越受到科研人员的重视。

目前国内外学者对磁力齿轮进行的理论与实验研究已取得了一些进展，并已将其应用于复合电机［5-6］、永磁无刷电机［7-8］、风力涡轮电机［9］中。虽然可以通过实验得到磁力齿轮的运行效率，但是在传动效率方面的研究主要是通过模拟和实验来进行［10-12］，而在理论方面，则主要是侧重有关输入转矩和输出转矩的理论计算［13］，文献［14］根据恒定磁场中的标量磁位理论，通过求解不同边界条件下的微分方程，获得调制式永磁齿轮中高速永磁圈在无调磁环状况下的气隙磁场数理模型。文献［15］对磁力齿轮进行了有限元模拟分析，通过瞬态分析方法，得到磁力齿轮的静态扭矩和功率损耗，得出其内、外转子扭矩的比值约等于传动比，且其静扭矩随转子的位置不同呈正弦曲线变化。文献［16］用有限元法比较了磁力齿轮不同充磁方式下磁场关系，其内外转子永磁体每一极下分别分成2块和3块，并对其模型在2-D和3-D下进行了分析。文献［17］是采用数值解析结合法计算具有两层气隙磁场的齿轮传动装置，气隙磁场用解析法表示，气隙区域无网格，转子可以自由转动，而含有非线性媒质的区域有限元法处理。文献［18］用有限元法分析了磁力齿轮不同传动比模型，分析结果是分数齿轮比有更好的性能，并且有较高的传递效率和稳定性能。但这些仅分析了不同传动比对其传动性能的影响，而结构参数对传动性能的影响研究甚少。

本文针对磁力齿轮结构的特殊性，对磁力齿轮两转子永磁体采用Halbach阵列充磁，建立Halbach充磁解析模型；应用全局解析法分析Halbach阵列同心式磁力齿轮。其次，详细分析了在传动比不变的情况下，调磁环铁心宽度、调磁环高度及外转子轭部厚度等参数与磁力齿轮最大静态转矩之间的关系。以一台内转子4对极、外转子17对极的Halbach阵列同心式磁力齿轮样机为例，计算了气隙磁场和电磁转矩，并与有限元法结果比较。合理选择结构参数可以提高磁力齿轮的转矩密度，为同心式磁力齿轮结构参数的设计与优化提供依据及方向。

1　解析模型

图1是Halbach阵列同心式磁力齿轮结构模型，共分为5个子区域，包括内外两层气隙子区域（II和III）、内外转子永磁体子区域（I和IV）和调磁定子槽子区域（i），其中R1～R6为相应各区域半径。内外转子磁极分别为4对极和17对极，调磁环齿数Q=21，内转子每极永磁体分为4小块，外转子每极永磁体分为2小块，图中箭头方向表示的是每一小块永磁体充磁方向。假设极对数p、每极均分m块数，则每块所占角度为

设起始块中心线位于x轴，且水平磁化方向。此时分两种情况，一是内转子永磁体磁化方向，二是外转子永磁体磁化方向。永磁体磁化方向表达式为

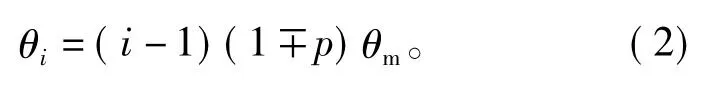
其中：i表示m块中的第i块；“-”表示的是内转子；“+”表示的是外转子。

每极平均分m块，每块占电角度180°/m。以第一块为基准，设相对转动角度为零度，接着第二块相对中心线转动角度为180°/m电角度。对于内转子而言，应转动负角度。于是第i块相对中心线转动角度为

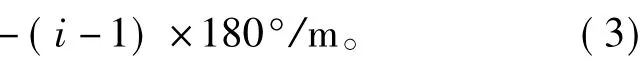
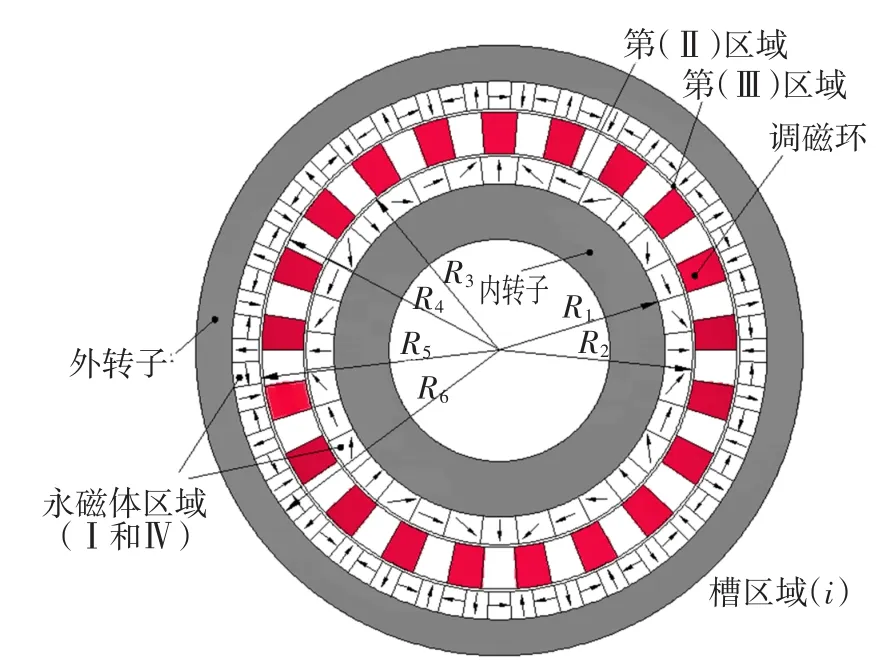
图1　Halbach阵列同心式磁力齿轮结构模型Fig.1　Geometry of the studied magnetic gear with Halbach arrays

图2为Halbach阵列同心式磁力齿轮内外转子某一对极下永磁体排列情况示意图，其中内转子每一对极下共有8小块永磁体；外转子每一对极下有4小块永磁体。

二维场中永磁体磁化强度M表达式为

其中：

式中：“+”代表外转子；“-”代表内转子；p是极对数；m为每一极下永磁体所分块数；k为m块中的第k块；θ0为永磁体中心线与基准线r轴初始位置角度；Br为永磁体剩磁；μ0为真空磁导率。

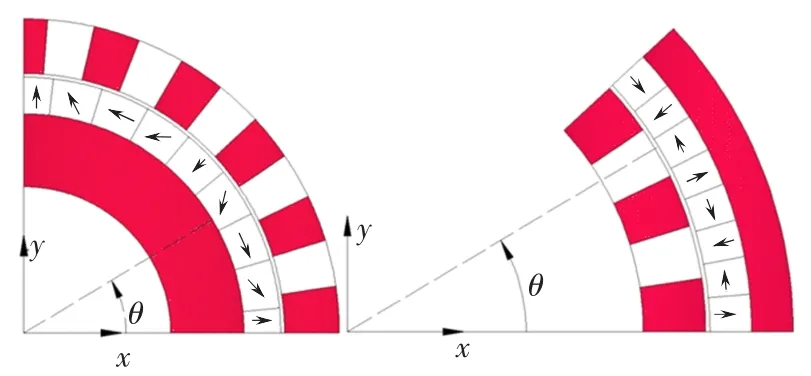
图2　Halbach永磁阵列排列Fig.2　Halbach permanent-magnet arrays

本文研究同心式磁力齿轮模型主要参数值如表1所示，对于该磁力齿轮模型来说，内转子4对磁极，外转子17对磁极，调磁环铁心数为21对，因此该磁力齿轮模型传动比为1∶4.25。

表1　磁力齿轮模型参数Table 1　Parameters of magnetic gear model

2　结构参数与转矩关系

电磁转矩是电机实现机电能量转换重要参数之一，准确计算磁力齿轮电磁转矩是设计、分析磁力齿轮的关键。根据麦克斯韦应力张量法理论，电磁转矩的大小与磁场有关，如何提高磁场强度就是解决问题的关键［19-21］。磁场强度的大小与气隙长度、永磁体厚度、调磁环高度、调磁环之间的宽度（即槽口宽度）、转子铁心轭部厚度及硅钢种类等都有关系。根据同心式磁力齿轮自身特点，选取以下几个结构参数作为优化变量。

2.1调磁环之间的宽度

一般的调磁环是由铁心块和非导磁材料等宽构成，由于调磁环铁心块宽度的变化（同样也可以理解为类似两块铁心之间的槽口宽度）不会引起磁力齿轮总体积的变化，因此应该通过优化设计选取合理的铁心块和非导磁材料宽度的比例，以提高磁力齿轮的转矩密度。通过全局解析法分别给β（槽口宽度）赋不同值，得到调磁环之间的槽口宽度对同心式磁力齿轮最大静态转矩的影响情况，如图3所示。

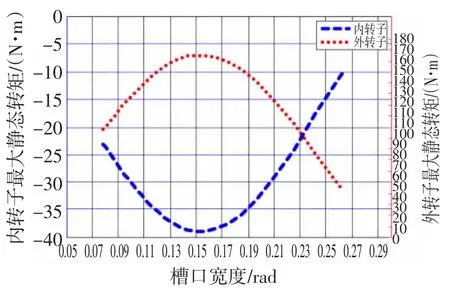
图3　槽口宽度对最大静态转矩的影响Fig.3　Influence of slot width on the maximum static torque

从图3可以看出，槽口的宽度对同心式磁力齿轮最大静态转矩有很大的影响，当槽口宽度在0.13～0.18 rad之间变化时，磁力齿轮获得较大的输出转矩。

2.2调磁环高度

调磁环的高度由外层气隙内半径与内层气隙外半径之间的差决定的。在研究调磁环高度对磁力齿轮电磁转矩的影响时，保持磁力齿轮外转子尺寸不变，在全局解析法中调整外层气隙内半径与内层气隙外半径的值时，同时调整内转子永磁体的厚度即R1与R2，使得内转子永磁体的体积保持不变，以消除内转子永磁体变化对计算结果的影响。此时计算结果如图4所示。

图4　调磁环高度对最大静态转矩的影响Fig.4　Influence of modulating ring height on the maximum static torque

从图4可以看到，调磁环的高度对磁力齿轮的最大静态转矩有一定影响，在设计同心式磁力齿轮时应当通过计算来确定调磁环的最佳高度。当调磁环高度在8～13 mm时，可以得到在同样体积下较大的输出转矩。

2.3外转子轭部厚度

在研究外转子轭部厚度对磁力齿轮电磁转矩的影响时，保持磁力齿轮其他设计参数不变，此时磁力齿轮外转子轭部厚度的变化会同时影响到齿轮的最大输出转矩和转矩密度。因为厚度的增加会增大磁力齿轮的体积，会使转矩密度降低。图5是最大静态转矩随外转子轭部厚度的变化情况。

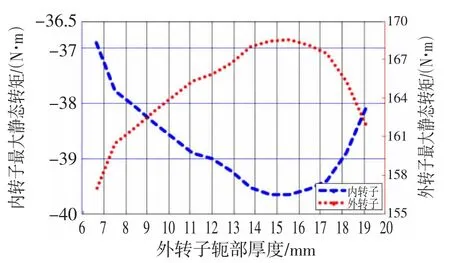
图5　外转子轭部厚度对最大静态转矩的影响Fig.5　Thickness of outer rotor yoke on the influence of the maximum static torque

从图5可以看出，同心式磁力齿轮的最大静态转矩随着外转子轭部厚度的增加而增加，但是当轭部厚度增加到一定程度时，其转矩值不在增加反而减小。虽然增加一定的外转子轭部厚度可以提高最大静态转矩，但是这也同时增大了磁力齿轮的体积，此时磁力齿轮的转矩密度随着轭部厚度的增加而降低。采用Halbach阵列充磁后，在不影响磁回路的情况下，转子轭部厚度可以相应的减少好多。同样外转子轭部处的磁密不会达到较大，不会出现过饱和，既节省了材料，减少了体积，又节约了成本。

3　计算实例及实验验证

为了验证本解析计算方法和优化设计的有效性，实验室制造了一台Halbach阵列同心式磁力齿轮样机。将内、外转子永磁体和调磁定子槽初始相位角均设为0°，该样机磁力线的分布情况如图6所示。从图中可知，在内、外转子轭部Halbach阵列充磁磁密较同部位径向充磁磁密小很多，因此转子材料有所减少，降低了体积及成本。

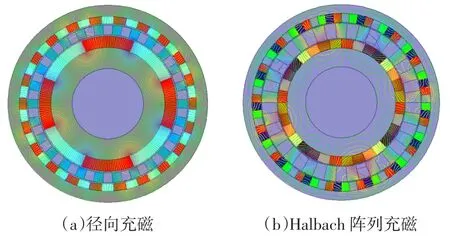
图6　磁力线的分布Fig.6　Calculated flux lines

图7、图8分别为样机内外两层气隙径向磁密和切向磁密解析计算结果和有限元计算结果的比较。

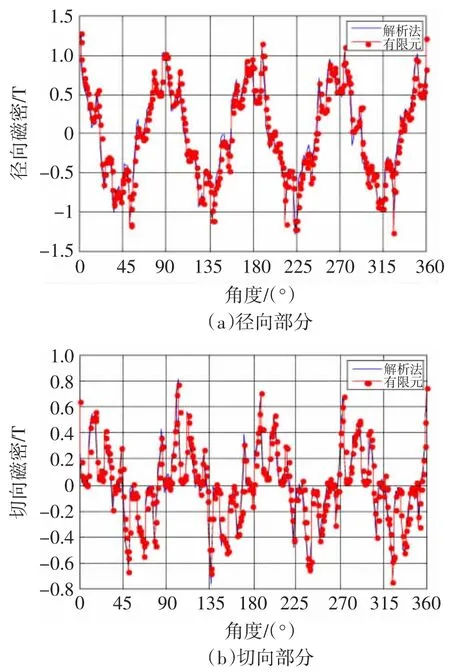
图7　内层气隙中间磁通密度Fig.7　Flux density distribution in the middle of the inner air-gap

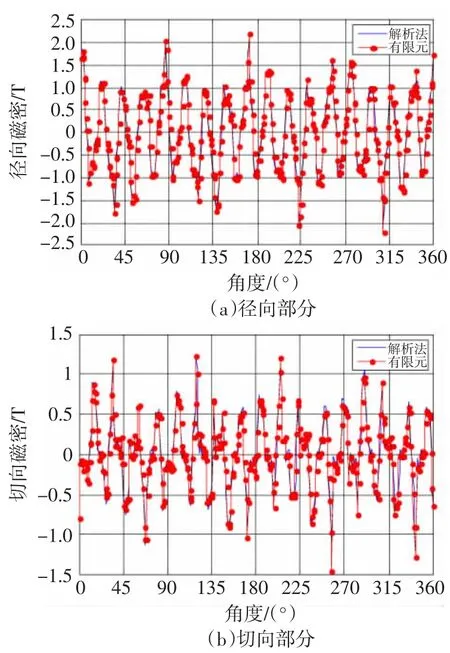
图8　外层气隙中间磁通密度Fig.8　Flux density distribution in the middle of the outer air-gap

从图7、图8可看到，全局解析法计算径向和切向磁密相对有限元计算结果在波形上吻合较好，这表明本解析方法是准确有效的。

对图7和图8中的气隙磁场径向磁密进行傅里叶分析，可以得到图9。

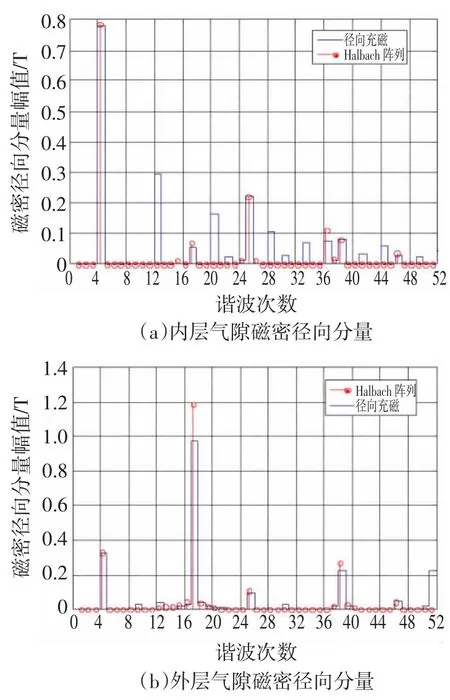
图9　气隙磁场傅里叶分解Fig.9　Air-gap magnetic field of Fourier decomposition

从图9（a）中可以得到，谐波次数4、17、25、38、46等为内层气隙转矩传递的有效谐波次数；谐波次数33、41、49等为转矩脉动的主要来源谐波；而在Halbach阵列充磁后，12、20、28、44、52等谐波均已消失，体现了此种充磁方式下谐波含量小的特点。从图9（b）中可以得到，谐波次数4、17、25、38、46等为外层气隙转矩传递的有效谐波次数；而在Halbach阵列充磁中，9、12、30、51等谐波均已消失。从傅里叶分析结果来看，Halbach阵列充磁后的同心式磁力齿轮，外层中间气隙磁密幅值较径向充磁大，且谐波所占比例要小很多。

固定调磁环和外转子永磁体的位置，每隔4.5°转动内转子永磁体，得到静态转矩波形，图10为结构参数优化后Halbach阵列充磁同心式磁力齿轮的内外转子静态电磁转矩。

图10　矩角特性Fig.10　Torque versus angle

从图10中可以看出，内、外转子转矩随转子转过一对磁极即90°的空间角度变化规律。转矩大小随着内、外转子永磁体相对位置的变化而变化，这与同步电机中的矩角特性相类似；内、外转子上的转矩波形均近似为正弦波，转矩比值在任意位置都保持在-1∶4.25，这与其传动比是一致的，且内转子永磁体在转到22.5°时得到最大静态转矩值。

图11为Halbach阵列同心式磁力齿轮结构参数优化后内、外转子输出转矩图。此时固定调磁环，内转子顺时针转动，而外转子逆时针转动，且转速满足关系式φo=-φipi/po。

图12为Halbach阵列同心式磁力齿轮样机实物照片。（a）图从左至右依次为端盖，外转子，外壳，内转子，调磁环；（b）图是装配好后的试验样机。

图13为样机试验平台，直流电机作为驱动，磁粉制动器作负载。图中从右至左依次为直流电机、小量程转矩传感器和显示仪、Halbach阵列同心式磁力齿轮、大量程转矩传感器和显示仪、磁粉制动器。其中直流电机作为原动机通过小量程转矩传感器与磁力齿轮内转子连接，根据小量程转矩传感器的转矩和转速可以得到磁力齿轮的输入功率；磁粉制动器作为负载通过大量程转矩传感器与磁力齿轮外转子连接，根据大量程转矩传感器的转矩和转速可以得到磁力齿轮的输出功率。

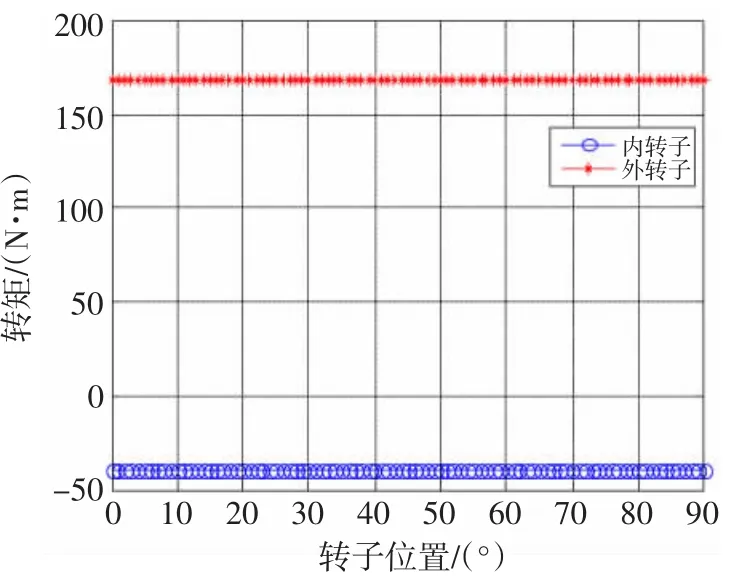
图11　转矩输出Fig.11　Electromagnetic torque exerted

图12　样机实物Fig.12　Photo of prototype

图13　试验平台Fig.13　Test bench

表2给出外转子负载侧转速为100 r/min时的负载实验结果。

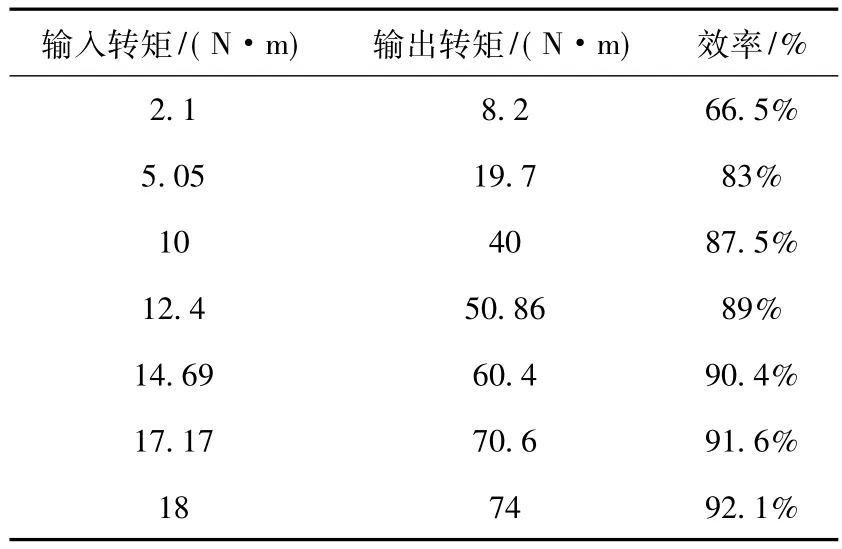
表2　负载侧转速为100 r/min时的效率Table 2　Efficiency of load side for 100 r/min

从样机带载试验结果知，Halbach阵列同心式磁力齿轮传动装置传递效率受负载大小影响很大，由于磁力齿轮的负载损耗与空载损耗基本上是一致的，因此负载轻时磁力齿轮传动装置效率较低；但损耗会随着转速的升高而增加，所以传动效率会随着转速的升高会降低。在低速外传子转速为20～150 r/min速度范围内，当负载转矩大于60 N·m时，其传递效率在90%以上。当负载转矩达到74 N·m时，样机的有效长度对应的输出转矩密度达到57.18 kN·m/m3。

4　结论

本文采用了二维全局解析法计算Halbach阵列同心式磁力齿轮磁场、建立了Halbach阵列充磁解析模型、分析了结构参数与电磁转矩之间的关系、计算了磁力齿轮电磁转矩。通过实例模型计算了内、外两层气隙磁场和内、外转子电磁转矩，其计算波形与有限元法计算波形结果一致，证明了解析法的正确性；从试验结果知，样机效率可以达到90%以上，但传动效率会随着转速的升高而降低。总之，结构参数的合理选取，可以有效提高磁力齿轮的转矩密度，同时节约成本，本研究对磁力齿轮的设计具有一定的参考价值。

［1］ATALLAH K，HOWE D.A novel high-performance magnetic gear ［J］.IEEE Transactions on magnetics，2001，37（4）：2844 -2846.

［2］RASMUSSEN P O，ANDERSEN T O，JORGENSEN F T，et al. Development of a high-performance magnetic gear［J］.IEEE Transactions on Industry Applications，2005，41（3）：764-770.

［3］涂小涛，辜承林.新型横向磁通永磁电机不同控制策略的对比实验［J］.电工技术学报，2012，27（3）：62-67. TU Xiaotao，GU Chenglin.Experimental research on control of novel transverse-flux permanent magnet motors［J］.Transactions of China Electrotechnical Society，2012，27（3）：62-67.

［4］ 刘哲民，陈谢杰，陈丽香，等.基于3D-FEM的新型横向磁通永磁电机的研究［J］.电工技术学报，2006，21（5）：19-23. LIU Zhemin，CHEN Xiejie，CHEN Lixiang，et al.Study of a new transverse flux permanent magnet machine based on 3D-FEM［J］. Transactions of China Electrotechnical Society，2006，21（5）：19 -23.

［5］HO S L，NIU S X，FU W N.Transient analysis of a magnetic gear integrated brushless permanent magnet machine using circuit-fieldmotion coupled time-stepping finite element method［J］.IEEE Transactions on Magnetics，2010，46（6）：2074-2077.

［6］张东，邹国棠，江建中，等.新型外转子磁齿轮复合电机的设计与研究［J］.中国电机工程学报，2008，28（30）：67-72. ZHANG Dong，ZOU Guotang，JIANG Jianzhong，et al.Design and research of a novel magnetic-geared outer-rotor compact machine［J］.Proceedings of the CSEE，2008，28（30）：67-72.

［7］CHAU K T，ZHANG D，JIANG J Z，et al.Design of a magnetic geared outer rotor permanent magnetic brushless motor for electric vehicles［J］.IEEE Transactions on Magnetics，2007，43（6）：2504-2506.

［8］FU W N，HO S L.A quantitative comparative analysis of a novel flux-modulated permanent-magnet motor for low-speed drive［J］. IEEE Transactions on Magnetics，2010，46（1）：127-134.

［9］LIU C H，CHAU K T，JIANG J Z，et al.Design of a new outer-rotor permanent magnet hybrid machine for wind power generation ［J］.IEEE Transactions on Magnetics，2008，44（6）：1494 -1497.

［10］SHAH L，CRUDEN A，WILLIAMS B W.A variable speed magnetic gear box using contra-rotating input shafts［J］.IEEE Transactions on Magnetics，2011，47（2）：431-438.

［11］井立兵，章跃进.同心式磁力齿轮磁场及转矩全局解析法分析［J］.中国电机工程学报，2012，32（30）：139-146. JING Libing，ZHANG Yuejin.An exact analytical method for magnetic field computation and electromagnetic torque in a concentric magnetic gear［J］.Proceedings of the CSEE，2012，32 （30）：139-146.

［12］LUBIN T，MEZANI S，REZZOUG A.Analytical computation of the magnetic field distribution in a magnetic gear［J］.IEEE Transactions on Magnetics，2010，46（7）：2611-2621.

［13］井立兵，章跃进，李琛，等.Halbach阵列同心式磁力齿轮磁场分析与优化设计［J］.中国电机工程学报，2013，33（21）：163-169. JING Libing，ZHANG Yuejin，LI Chen，et al.Magnetic field computation and optimization design for a concentric magnetic gear With Halbach permanent-magnet arrays［J］.Proceedings of the CSEE，2013，33（21）：163-169.

［14］葛研军，聂重阳，辛强.调制式永磁齿轮气隙磁场及转矩分析计算［J］.机械工程学报，2012，48（11）：153-158. GE Yanjun，NIE Chongyang，XIN Qiang.Analytical calculation of air-gap magnetic field and torque of modulated permanent magnetic gears［J］.Chinese Journal of Mechanical Engineering，2012，48（11）：153-158.

［15］杨超君，李直腾，李志宝，等.高性能磁力齿轮传动扭矩与效率的数值计算［J］.中国电机工程学报，2011，31（32）：107-114. YANG Chaojun，LI Zhiteng，LI Zhibao.Numerical calculation of driven torque and efficiency of a high-performance magnetic gear ［J］.Proceedings of the CSEE，2011，31（32）：107-114.

［16］JIAN L N，CHAU K T，GONG Y，et al.Comparison of coaxial magnetic gears with different topologies［J］.IEEE Transactions on Magnetics，2009，45（10）：4526-4529.

［17］杜世勤，江建中，章跃进，等.一种磁性齿轮传动装置［J］.电工技术学报，2010，25（9）：41-46. DU Shiqin，JIANG Jianzhong，ZHANG Yuejin，et al.A magnetic gearing［J］.Transactions of China Electro-technical Society，2010，25（9）：41-46.

［18］FRANK N W，TOLIYAT H A.Gearing ratios of a magnetic gear for marine applications［C］//Electric Ship Technologies Symposium.Maryland，USA.2009：477-481.

［19］李亚西，朱峰，朱晓光，等.一种消除双馈电机转矩脉动的磁场重构方法［J］.电工技术学报，2011，26（7）：161-166. LI Yaxi，ZHU Feng，ZHU Xiaoguang，et al.A field reconstruction method for elimination of torque ripple in doubly fed induction generators［J］.Transactions of China Electrotechnical Society，2011，26（7）：161-166.

［20］章跃进，李春江，屠关镇，等.面贴式永磁力矩电机气隙主磁场解析数值分析法［J］.电工技术学报，2011，26（9）：13 -17. ZHANG Yuejin，LI ChunJiang，TU Guanzhen，et al.Analytical method for air-gap main magnetic field computation of surface mounted permanent magnet torque motors［J］.Transactions of China Electro-technical Society，2011，26（9）：13-17.

［21］宋帅，张英敏，李兴源.考虑感应电动机故障中电磁转矩变化的节点暂态电压评估方法［J］.电力系统保护与控制，2013，41（17）：103-108. SONG Shuai，ZHANG Yingmin，LI Xingyuan.Assessment method of transient voltage stability of load bus considering the changing of induction motor［J］.Power System Protection and Control，2013，41（17）：103-108.

（编辑：刘琳琳）

Parameters analysis and optimization design for concentric magnetic gear with halbach permanent-magnet arrays

JING Li-bing1，2， LIU Lin1， ZHANG Yue-jin3， SU Jian-hua4
（1.College of Electrical Engineering and New Energy，China Three Gorges University，Yichang 443002，China；2.Hubei Micro-grid Engineering Technology Research Center，Yichang 443002，China；3.Mechatronics and Automation College，Shanghai University，Shanghai 200072，China；4.The 27th Research Institute of China Electronics Technology Group Corporation，Zhengzhou 450047，China）

Concentric magnetic gears hold a promising future in low speed high torque field.In order to obtain a sinusoidal distribution of air gap magnetic field，exact 2-D analytical method was proposed to calculate the magnetic field distribution in a concentric magnetic gear with Halbach permanent-magnet arrays，and the relationship between the parameters and maximum static torque was analyzed.The parameters include width of modulating ring core，height of modulating ring and thickness of outer rotor yoke. Compared air-gap magnetic field distributions computed by the analytical method with those obtained from the 2-dimensional finite element method（FEM），the waveform shows good agreement with the measured waveform，which proves the proposed method is correct and effective.According to the results of parameters analysis，the concentric magnetic gear prototype was produced，which the numbers of pole pairs on the inner and outer rotors are 4 and 17，respectively.The test results show reasonable structural parameters improve the torque density of magnetic gears，and the design of magnetic gear provides a useful reference.

concentric magnetic gear；Halbach arrays；exact analytical method；air-gap magnetic field；torque density；modulating ring

10.15938/j.emc.2016.03.002

TM 351

A

1007-449X（2016）03-0006-07

2014-05-25

国家自然科学基金（51177097）；湖北省自然科学基金（2014CFC1143）；湖北省微电网工程技术研究中心开放基金资助项目（2015KDW03）；三峡大学人才基金项目（KJ2013B078）

井立兵（1982—），男，博士，讲师，研究方向为特种电机设计与优化，电机电磁场分析计算；

柳霖（1990—），男，硕士研究生，研究方向为电机内电磁场的数值分析与电机的优化设计；

章跃进（1956—），男，博士，教授，博士生导师，研究方向为电机电磁场数值、解析法研究及其电机动态仿真研究；苏建华（1982—），男，硕士，工程师，研究方向为纯电动车辆系统技术，电机驱动控制等。

井立兵