基于改进蚁群算法的UUV三维路径规划方法

温志文, 蔡卫军, 杨春武



基于改进蚁群算法的UUV三维路径规划方法

温志文1,2, 蔡卫军1, 杨春武1

(1. 中国船舶重工集团公司 第705研究所, 陕西 西安, 710077; 2. 水下信息与控制国家重点实验室, 陕西 西安, 710077)

路径规划是水下无人航行器(UUV)研究领域的重要课题之一。针对已有蚁群算法在采用加权和法处理多个目标同时优化的路径规划问题时出现加权系数取值不确定性、目标函数偏离理想值、算法运行效率较低等问题,以及为了避免蚁群算法收敛速度慢, 容易陷入局部最优, 提出了一种基于改进蚁群算法的路径规划方法。该方法基于Pareto非劣最优解集的思想对多个目标进行优化组合, 同时加入了趋向位置目标的吸引策略, 有效克服了上述缺陷。3D环境下的仿真试验证明了该方法的有效性和可行性。

水下无人航行器(UUV); 路径规划; 蚁群算法; 多目标优化

0 引言

水下无人航行器(underwater unmanned vihicle, UUV)在复杂海洋环境下执行各种使命时, 首先要具备绕过障碍物向目标靠近的能力, 即自主导航与避障能力。UUV路径规划任务需要在安全航行区域内, 按一定的优化准则搜索一条从指定起始点到目标点的最优路径(或次优路径)。目前用于全局路径规划的方法主要有人工势场法、A*搜索算法、神经网络技术等[1]。人工势场法简单易行, 但容易陷入局部最优[2]; A*搜索算法随着维数的增加, 算法的时空要求将很难得到满足[3]; 遗传算法计算量大, 在解决多目标优化问题时常出现易收敛到局部最优值的情况。文献[4]采用粒子群算法对有限数目的采样航点进行优化, 使用高次B样条曲线拟合出满足路径最短且威胁最小的无人战斗机3D飞行路径, 文献[5]采用遗传算法对AUV的3D路径规划进行了研究, 得到了具有不同特点的最优3D路径。相较于2D空间环境, 3D空间规划增加了空间的复杂性, 更适用于实际情况, 也对算法的搜索效率提出了较高要求。

蚁群算法是一种启发式搜索算法, 具有较强的鲁棒性、优良的分布式计算以及易于与其他算法结合等优点[6]。其生物机理是蚂蚁在蚁巢与食物源间寻觅一条最短的可行路径, 这恰好与路径规划的物理过程不谋而合, 同时, 二者在内部机理上的天然联系, 也为基于蚁群算法的路径规划研究提供了有力依据[7]。

在实际的UUV路径规划过程中, 路径性能要求存在多个目标, 如路径最短、规划时间最优、安全性能最好、能源消耗最小等, 但这些目标之间往往存在着冲突[8]。现有的蚁群算法处理方法主要采用加权和法[9], 加权和法简单直接地打乱了多个目标之间的制约关系, 从而使目标函数偏离理想值, 加权系数取值需要依靠先前经验, 算法运行效率较低, 导致了优化算法寻优效果出现偏差。

文中通过借鉴多目标优化算法中Pareto非劣最优解集的思想, 提出一种基于改进蚁群算法的路径规划方法, 对多个目标同时优化的UUV路径规划问题进行研究。同时加入趋向位置目标的吸引策略, 提高了算法收敛速度, 从而避免搜索陷入局部最优。

1 3D环境建模

目前电子海图在水中兵器的应用处于探索阶段, 由于电子海图的复杂性, 通常需要将电子海图转换成可以直接利用的海图数据环境模型。

文中采用海图信息栅格化方法对某海域的数字海图进行渲染, 首先将3D规划空间均匀分解成××个等大小的单元, 以栅格单元为路径规划中的最小移动单位, 栅格分辨率为1 km。如果某个栅格属于碰撞区, 记为1类栅格; 如不属于碰撞区则记为0类栅格, 以此表示海图的碰撞区信息; 其次对碰撞区进行处理、合并，消除不可航行路段和陷阱路段, 将碰撞区规范成多边形图形, 这样构建出的数据空间包含了标识起始点、目标点、障碍区、威胁区以及航路位置信息,可方便利用算法进行路径规划。文中对环境模型作如下假设。

1) 将UUV视为质点, 规划路径的长度在UUV航程内, 且UUV具有原地转向和垂直爬升的性能。

2) 规划环境为静态3D空间, 将障碍物和危险区域视为碰撞区, 将不规则碰撞区“膨化”处理为立方体(这里假设规划空间的长宽高相同)。

3) 不考虑潮流、海流、电子干扰等其他干扰因素的影响。

胡四一强调，水是生命之源、生产之要、生态之基，解决我国日益复杂的水资源问题，实现水资源高效利用和有效保护，根本上要靠制度、靠政策、靠改革。《意见》这一水资源纲领性文件的出台和实施，将极大地推动该项制度贯彻落实，促进水资源合理开发利用和节约保护，保障经济社会可持续发展。

将每个栅格的中心作为规划算法中1个计算单位, 称为“路径节点”。在文中取, 根据从左至右、从下至上的原则为每个栅格编号, 每个栅格具有1~1 000之间的唯一编号。每个栅格在3D空间中的坐标用栅格中心点的位置来表示, 栅格序号与3D坐标的对应关系由式(1)和式(2)决定。

文中用路径栅格节点序号表示UUV最终的路径规划结果, 如, 其中为起始点栅格编号,为目标点栅格编号,为中间路径节点栅格编号。

和栅格有关的示意图分别见图1和图2。

2 改进蚁群算法设计

2.1 基于非劣解集的改进蚁群算法

文中以UUV的路径长度、路径平滑度、安全性和规划时间的最优组合为规划目标。UUV路径的安全性是以UUV躲避碰撞区的能力来衡量,要求规划出的路线有效避开碰撞区。路径长度的评价函数为各路径节点之间的距离和。路径平滑度的评价函数为路径转弯角度值的函数。通过将路径安全度合理转化为对障碍区和威胁区的规避能力后, 路径规划目标函数为路径长度与路径平滑度这2个评价指标的优化组合, 同时考虑了算法的运行效率, 即规划时间。这就需要对以上几个目标同时进行优化, 即多目标优化。

目标函数的数学描述为

其中, 目标函数的3个分向量分别如下。

2) 规划路径平滑度

文中提出基于非劣解集思想的多目标蚁群优化算法, 对多个目标同时优化流程如下。

Step1: 准备2个外部非劣解集，分别命名为解集1和解集2。解集1用于存储每次迭代完成后得到的较优解, 解集2用于存储所有迭代循环结束后得到的较优解;

Step2: 外部非劣解集只允许两类解进入：一类是目标函数的3个分向量评价指标都优于已有解集, 同时把处于劣势的解集从外部非劣解集中删除; 另一类是与已有解集相比较, 在保证其中一些分向量评价指标不处于劣势的前提下, 另一些分向量评价指标处于优势;

Step3: 算法开始进行1次迭代循环。首先,将第1个蚂蚁找到的路径作为1个解存储到解集1中, 然后依次将其他蚂蚁寻优得到的解按Step2的准则与解集1中已有的解进行比较, 本次循环完成后更新解集1;

Step4: 将第1次循环完成后解集1中的解存储到解集2中, 按Step3进行下一次循环。待下一次循环完成后, 将更新后解集1中的解按Step2的准则与解集2中已有的解进行比较, 同时更新解集2;

Step5：直到所有迭代循环完成后, 非劣解集2中存储的解即为路径规划目标函数的解。

显然, 对于多目标优化问题, 并没有真正的最优解, 所以每次蚁群算法优化完毕后外部非劣解集2中存储的解不可能唯一, 其中的每一个解都为本次路径规划的较优解。

2.2 趋向位置目标的吸引策略

其中,(,)为当前节点与下一节点之间的距离。

这种选择方式使得蚂蚁总是会优先选择与当前节点距离最近的待选栅格, 忽略了路径规划全局性寻优的需求。按此方法寻找到的规划路径往往会出现“兜圈子”的情况, 致使算法不仅搜索速度慢, 而且得不到全局最优路径。针对上述问题, 将能见度重新定义为与当前节点和目标节点之间的距离有关, 采用这一策略, 蚂蚁将不再盲目进行搜索, 而是优先选取待选路径节点中与目标点距离最近的节点, 提高了算法搜索速度和全局寻优能力。新的转移概率公式与能见度定义分别为

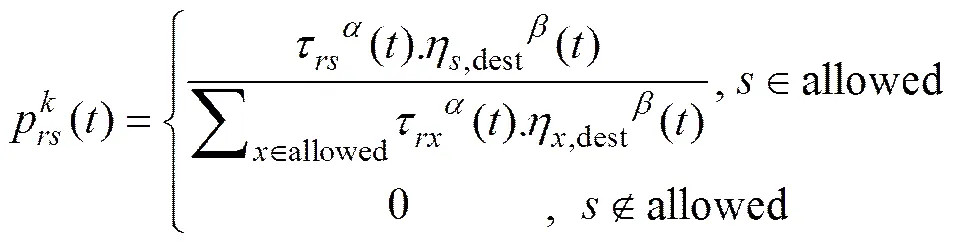
采用这一策略后, 蚂蚁不再盲目地进行路径搜索, 而是优先选择待选栅格集中离目标点最近的栅格, 因此称该策略为位置目标吸引策略。位置目标吸引策略将大大提高算法搜索速度, 增强了蚂蚁寻优的“方向性”, 同时避免算法陷入局部最优。

2.3 算法流程设计

改进后的蚁群算法流程图如图3所示。

3 仿真试验及分析

为验证文中改进蚁群算法的可行性与有效性, 进行了对比仿真试验。仿真结果参见表1。试验采用MATLAB仿真平台, 运用上述建立的3D空间环境模型。蚁群算法使用经过试验测试的参数: 蚂蚁数量, 迭代循环次数为50,, 初始信息素, 标准值0。

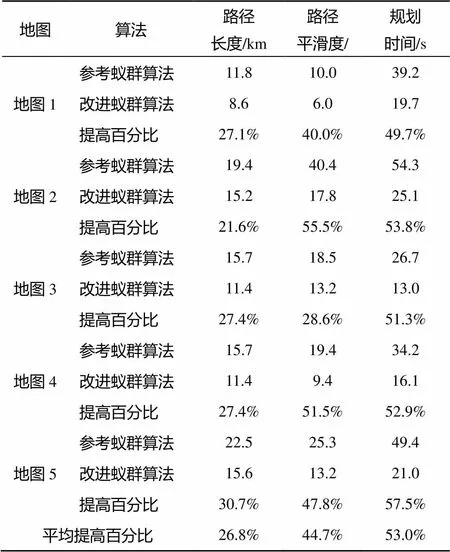
表1 仿真试验结果

文中采用文献[10]中已有的改进蚁群算法作为对比, 并将其命名为参考蚁群算法以示区别。

定义1: 各代平均代价函数值指每次循环搜索完成后, 所有蚂蚁规划路径长度的平均值。

定义2: 各代最优路径的代价函数值指每次循环搜索完成后, 所有蚂蚁规划路径长度的最小值。

仿真试验表明, 2种算法都能找到UUV从起点到终点的有效路径, 但从表1可以看出, 改进蚁群算法规划出的UUV路径长度比参考蚁群算法规划出的UUV路径长度平均提高了26.8%。从图8的各代平均代价函数值可以看出的各代平均代价函数值,改进蚁群算法的各代平均代价函数值均优于参考蚁群算法,改进蚁群算法更能有效地找到较优解, 有效避免了陷入局部最优。从图9各代最优路径的代价函数值可以看出, 改进蚁群算法在第2次迭代就可以找到长度最短的路径, 而参考蚁群算法需要将近10次迭代才能找到长度最短的路径, 改进蚁群算法搜索效率高于基本蚁群算法。

在参考蚁群算法中, 蚂蚁选择下一路径节点时, 只考虑当前节点与下一节点之间的距离, 忽视了全局路径规划“方向性”和“全局性”的要求, 导致出现了很多“拐点”, 甚至出现“绕弯子”的情况。而改进蚁群算法中, 蚂蚁选择下一路径节点考虑了与目标点之间的距离, 赋予蚂蚁具有“方向性”的特点, 避免了“绕弯子”的情况, 有效缩短了规划路径长度。在路径平滑度以及规划时间方面, 更是以44.7%和53.0%的提高幅度远远优于参考蚁群算法, 加快了算法搜索速度, 实现了UUV路径长度、平滑度和安全度多个目标的同时优化。参考蚁群算法仅仅以UUV路径长度作为评价路径规划好坏的标准, 不能将优化问题考虑全面, 文中则采用非劣解集的改进蚁群算法, 同时对多个目标进行优化组合, 在保证路径长度非劣的情况下, 对UUV路径平滑度和规划时间也进行了优化, 规划出的路径更具实用性。

4 结束语

针对已有蚁群算法在采用加权和法处理多个目标同时优化的路径规划问题时出现的一系列问题, 基于栅格化数字海图环境模型, 借鉴多目标优化算法中Pareto非劣最优解集的思想, 同时加入了趋向位置目标的吸引策略, 采用改进的蚁群算法对UUV路径规划方法进行了研究。仿真试验结果表明, 改进后的蚁群算法提高了算法搜索效率、避免蚁群算法陷入局部最优、能有效处理多个目标优化组合的UUV路径规划问题。

[1] 柳长安. 无人机航路规划方法研究[D]. 西安: 西北工业大学, 2003.

[2] 李晓丽, 谢敬, 傅卫平, 等. 一种改进势场法在多移动机器人避碰规划中的应用[J]. 计算机工程与应用, 2005, 41(17): 56-58.
Li Xiao-li, Xie Jing, Fu Wei-ping, et al. An Evolutionary Artificial Potential Field Method Used to Obstacle- avoidance Planning of Multiple Mobile Robots[J]. Com- puter Engineering and Applications, 2005, 41(17): 56-58.

[3] 漆阳华, 杨战平, 黄清华. A*的改进路径规划算法[J].信息与电子工程, 2009, 7(4): 326-329.
Qi Yang-hua, Yang Zhan-ping, Huang Qing-hua. Improved Path Planning Algorithm Based on A* Algorithm [J]. Information and Electronic Engineering, 2009, 7(4): 326-329.

[4] 张雷, 王道波, 段海滨. 基于粒子群优化算法的无人战斗机路径规划方法[J]. 系统工程与电子技术, 2008, 30(3): 506-510.
Zhang Lei, Wang Dao-bo, Duan Hai-bin. Study on Unin- habited Combat Arial Vehicle Path Planning Method Based on |Particle Swarm Optimization Algorithm[J]. Systems Engineering and Electronics, 2008, 30(3): 506- 510.

[5] 郝燕玲, 张京娟. 基于遗传算法的AUV三维海底路径规划[J]. 中国工程科学, 2003, 5(11): 56-60.
Hao Yan-ling, Zhang Jing-juan. AUV Path Planning in 3D Seabed Environment Using Genetic Algorithm[J]. Engi- neering Science, 2003, 5(11): 56-60.

[6] 段海滨. 蚁群算法原理及其应用[M]. 北京: 科学出版社, 2005.

[7] 张银玲, 牛小梅. 蚁群算法在移动机器人路径规划中的仿真研究[J]. 计算机仿真, 2011, 28(6): 231-234.
Zhang Yin-ling, Niu Xiao-mei. Simulation Research on Mobile Robot Path Planning Based on Ant Colony Optimization[J]. Computer Simulation, 2011, 28(6): 231-234.

[8] 赵涛, 刘明雍, 周良荣. 自主水下航行器的研究现状与挑战[J]. 火力与指挥控制, 2010, 35(6): 1-6.
Zhao Tao, Liu Ming-Yong, Zhou Ling-Rong. A Survey of Autonomous Underwater Vehicle Recent Advances and Future Challenges[J]. Fire Control & Command Control, 2010, 35(6): 1-6.

[9] 唐良, 方廷健. 基于改进蚁群算法的路径规划方法[J]. 中国科学技术大学学报, 2009, 39(9): 980-983.
Tang Ling, Fang Ting-Jian. Path Planning Method Based on Improved ant Colony Algorithm[J]. Journal of University of Science and Technology of China, 2009, 39(9): 980-983.

[10] 胡荟, 蔡秀珊. 机器人三维路径规划问题的一种改进蚁群算法[J]. 计算机工程与科学, 2012, 34(11): 153-157.
Hu Hui, Cai Xiu-shan. An Improved Ant Colony Algo- rithm for Three-dimensional Path Planning of Robots[J]. Computer Engineering and Science, 2012, 34(11): 153- 157.

Three-dimensional Path Planning Method Based on Improved Ant Colony Algorithm for UUV

WEN Zhi-wen1,2, CAI Wei-jun1, YANG Chun-wu1

(1. The 705 Research Institute, China Shipbuilding Industry Corporation, Xi′an 710077, China; 2. Science and Technology on Underwater Information and Control Laboratory, Xi′an 710077, China)

A path planning method based on improved ant colony algorithm is presented for an UUV to solve the problem that the current ant colony algorithm exists uncertainty of weight coefficient, deviation of objective function values from ideal value, low efficiency, slow convergence speed, and possibility falling into local optimum in dealing with the path planning of multi-objective optimization by using its weighted sum method. This method optimizes the combination of multiple objectives according to the idea of Pareto noninferior optimal solution set, and applies the attraction strategy of trend position object to effectively overcome the above defects. Simulation experiment in three-dimensional environment shows that the present method is effective and feasible.

underwater unmanned vehicle(UUV); path planning; ant colony algorithm; multi-objective optimization

10.11993/j.issn.1673-1948.2016.02.008

TJ630.33

A

1673-1948(2016)02-0120-06

2016-03-02;

2016-03-21.

. 温志文(1992-), 男, 在读硕士, 主要研究方向为鱼雷总体技术.

(责任编辑: 杨力军)