厚钢板疲劳裂纹扩展前缘应力状态试验与数值仿真

党之凡，乐京霞，董岩

武汉理工大学交通学院，湖北武汉430063

厚钢板疲劳裂纹扩展前缘应力状态试验与数值仿真

党之凡，乐京霞，董岩

武汉理工大学交通学院，湖北武汉430063

复杂的环境载荷不可避免地会造成海洋结构物的疲劳损伤，而高强度厚钢板典型的三向应力状态会增加结构脆性，更加缩短结构的疲劳寿命。为研究厚板裂纹前缘应力状态沿板厚方向的分布，完成了3组36 mm板厚Q370QE高强度钢的标准疲劳裂纹扩展速率试验，得到了材料参数C，m以及应力强度因子门槛值。接着，应用有限元方法分别基于线弹性分析和塑性分析计算裂纹尖端应力强度因子和裂纹尖端局部约束因子，并解释试验中裂纹前缘由倾斜趋于平直的现象。计算所得裂纹尖端应力强度因子可描述板厚中心部分裂纹前缘的应力状态，但在试件表面处结果失真，而裂纹前缘局部约束因子因考虑了厚板的厚度效应，故沿板厚方向分布的裂纹尖端局部约束因子可有效量化裂纹尖端的应力状态分布。

疲劳裂纹扩展速率试验；有限元分析；裂纹前缘应力状态；应力强度因子；局部约束因子

网络出版地址：http://www.cnki.net/kcms/detail/42.1755.TJ.20160317.1056.016.html期刊网址：www.ship-research.com

引用格式：党之凡，乐京霞，董岩.厚钢板疲劳裂纹扩展前缘应力状态试验与数值仿真［J］.中国舰船研究，2016，11（2）：51-57. DANG Zhifan，YUE Jingxia，DONG Yan.Investigation on the stress state along the crack front in the fatigue crack growth rate test for thick high strength steel plates［J］.Chinese Journal of Ship Research，2016，11（2）：51-57.

0　引　言

高强度厚钢板在海洋工程结构物中的使用越来越广泛。然而随着海洋结构物的深海化，其结构所承受的复杂海洋环境和极限载荷不可避免地会带来结构的疲劳和断裂问题。这一现象在厚板焊缝中尤为突出，因为厚板典型的三向应力状态会使塑性变形吸收能量的效果降到最低，并且增加结构的脆性。

疲劳裂纹扩展理论（FCP）是以断裂力学理论为基础的，通过Paris公式，可以清楚、直观地描述裂纹稳定扩展阶段的扩展速率［1］。

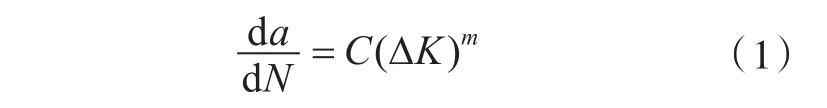
疲劳裂纹扩展理论的“相似概念”认为，相同材料的不同结构形式的裂纹在相似的循环载荷作用下，会有相同的疲劳裂纹扩展速率（FCGR）［2-3］。然而，由于厚钢板裂纹尖端区域存在平面应变状态，相比薄钢板的平面应力状态，在相同的应力强度因子K下FCGR不同。这意味着“相似概念”不适用于不同厚度的情况［2］。研究表明，FCGR应由应力强度因子幅值ΔK、载荷比R和厚度B这3个参数隐式表征［4］，而若板足够厚而使裂纹尖端处于平面应变状态，则仅ΔK和R这2个参数便可表征FCGR。Costa和Ferreira［5］对45#钢在不同板厚和载荷比R下进行了FCGR试验，发现FCGR随着试件板厚的增加而增大。Wolf［6］依据疲劳裂纹扩展时的裂纹闭合效应提出了一种FCGR模型，表达式为：

式中：U=0.5+0.4R。

本文将以FCGR标准试验研究为起点，对3个相同尺寸、厚度为36 mm的Q370QE高强度钢（屈服应力为400 MPa）试件进行试验，分别在恒幅载荷试验阶段和降力试验阶段获得Paris公式中的C 和m这2个材料参数以及疲劳裂纹扩展门槛值ΔKth。然后，运用有限元方法分析裂纹前缘应力强度因子和局部约束因子的分布状况来定量描述直裂纹前缘在疲劳裂纹扩展时的应力状态。

1　疲劳裂纹扩展速率试验

本试验所使用试件类型为单边缺口三点弯曲试件（SEN），该试件加工方便，对试验条件要求相对较低，适于厚钢板的FCGR试验。本FCGR试验所采用的标准——GB/T 6398-2000［7］与ASTME647（1995a）有相同的试验技术细节，但前者将SEN试件列为试验标准试样。材料的力学性能如表1所示。

表1　材料力学性能Tab.1　Material property

试件尺寸及机加工缺口尺寸如图1所示。

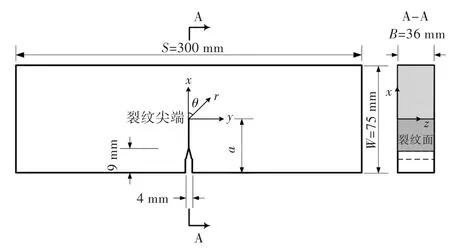
图1　试件及缺口尺寸Fig.1　Dimensions and coordinate system of the specimen

图2所示为裂纹长度和循环次数之间的对应关系。用割线法对有效数据进行处理，并且根据《金属材料疲劳裂纹扩展速率试验方法》（GB/T 6398-2000），对于SEN试件，应力强度因子幅值由式（3）计算得到。

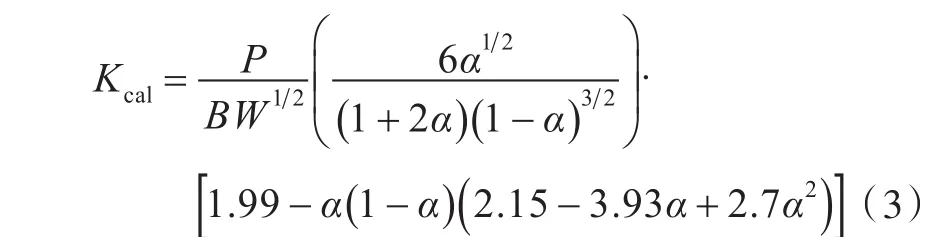
式中：P为载荷大小；B为试件厚度；W为试件宽度；α=a/W ，其中 a为裂纹长度，式（3）在0.3≤α≤0.9范围内有效。0

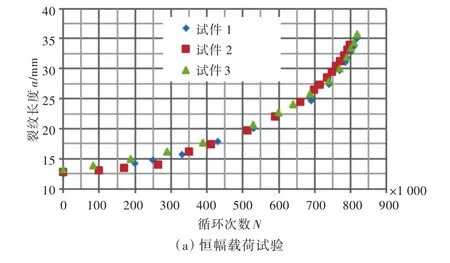
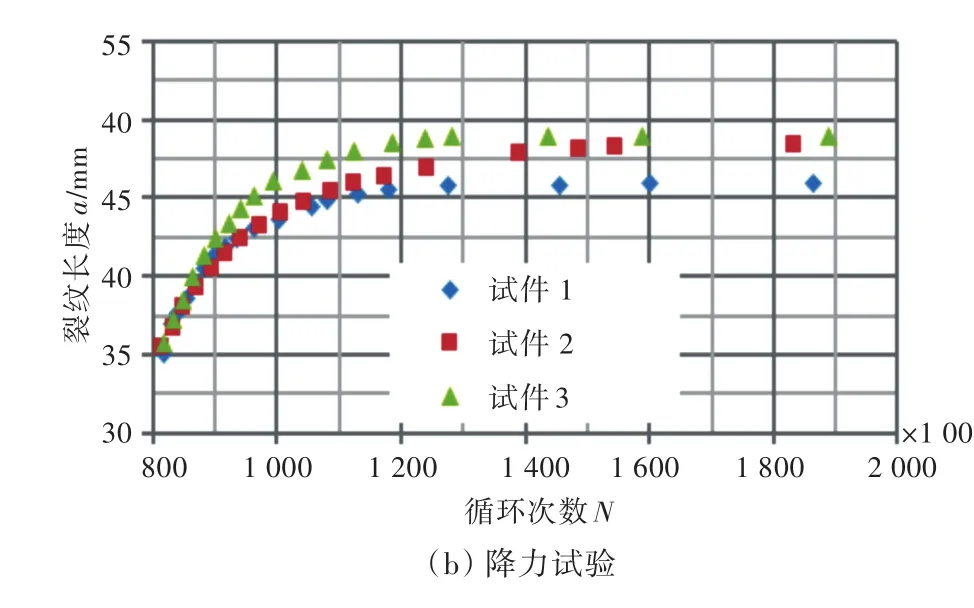
图2　裂纹长度和循环次数的对应关系Fig.2　Test results of two stage：（a）constant amplitude；（b）decreasing amplitude

通过线性拟合恒幅载荷试验的应力强度因子幅值与裂纹扩展速率之间的关系，得到C和m这2个材料参数，如表2所示。

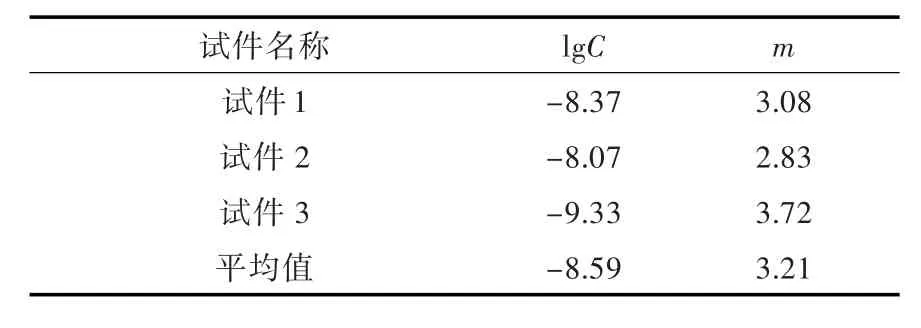
表2　恒幅载荷试验所测得的材料参数Tab.2　Material parameters C and m obtained in constant amplitude stage

降力试验时，记录后2级载荷起始裂纹长度和对应的循环载荷幅值，计算其所对应的ΔKk-1和ΔKk，取其平均值即为门槛值。

疲劳裂纹扩展门槛值ΔKth是用来描述宏观裂纹萌生的临界值。宏观裂纹的扩展行为可以用应力强度因子K来描述。由于微观裂纹和大范围屈服的宏观裂纹尖端的应力应变场与门槛值没有直接关系，故ΔKth的推导应在裂纹有一定长度下进行［8］。降力试验是测量门槛值的常用方法。降力试验中，在保持载荷比R不变的条件下，逐次降低应力强度因子幅值，直到平均裂纹扩展速率da/dN接近10-7mm/cycle时，降力试验结束。为了减小上一级过载对裂纹扩展的滞后作用，每一级载荷下都要使裂纹扩展增量Δa大于上一过载的塑性区尺寸［9］。试验结果如表3所示。

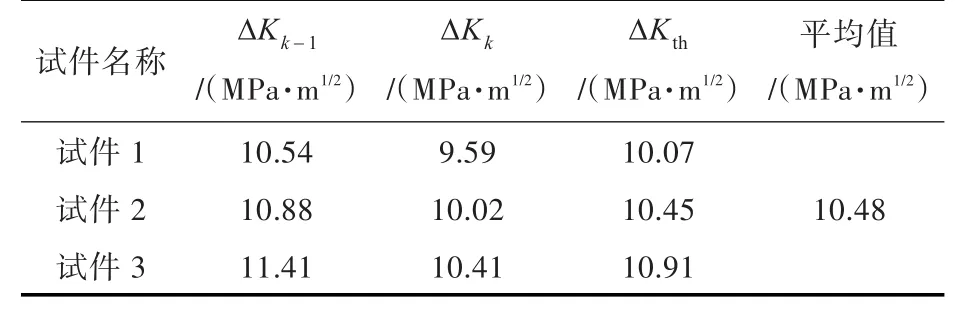
表3　降力试验所测得的门槛值Tab.3　Threshold of SIF amplitudeΔKthobtained in decreasing amplitude stage

基于线弹性断裂力学理论，要求塑性区尺寸不超过试件塑性区尺寸和断裂韧性的一定比例，即避免大范围的屈服。对SEN试件，规定

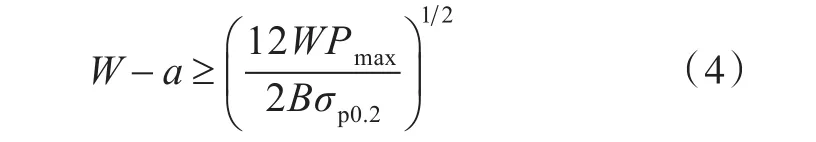
式中：Pmax为循环载荷的最大载荷；σp0.2为试件塑性区尺寸非比例伸长0.2%时的应力。故根据式（4）可知，当裂纹长度已知时，最大载荷值应满足

图3示出了试验最大疲劳载荷值和标准所允许的最大载荷随裂纹长度的检验结果。

图3　最大载荷检验Fig.3　Test loads during crack growing

在FCGR试验中，试件2个侧面的裂纹长度存在着明显的差异，可以证明裂纹前缘至少是倾斜的，测量结果如图4所示。但是，结合以上2图可以发现，当最大疲劳载荷接近标准规定的最大疲劳载荷时，两侧裂纹长度差值达到最小，倾斜裂纹趋向于平直。这一试验现象与苗张木［10］在预制测量裂纹尖端张口位移试验的试件裂纹时的发现相似。

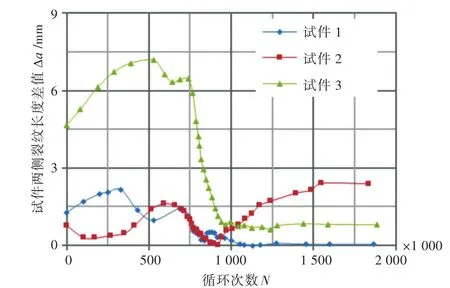
图4　试件两侧裂纹长度差值Fig.4　Different crack depth between two surfaces

2　三维裂纹尖端应力状态分析

2.1线弹性分析

为研究FCGR试验中裂纹尖端的应力状态，本文首先使用有限元分析软件ANSYS对试验试件的裂纹尖端区域进行弹性分析。

在有限元模型中，考虑到裂纹前缘的形状，分别将裂纹前缘简化为1条直线、1条与试件表面呈一定角度的直线以及由试件剖面所量得裂纹前缘线的曲线。采用倾斜裂纹模型的原因是，试验中，2个表面裂纹长度的差值最大达到了7.6 mm，而曲率的变化并不会使裂纹长度尺寸沿厚度方向发生太大的改变，其在真实反应试验现象的同时简化了模型。试件剖面如图5所示。

图5　试件裂纹前缘线Fig.5　Crack fronts of the specimen

有限元模型计算材料性能参数如表1所示。

许多研究表明，裂纹尖端的奇异性可以通过将20节点Solid 186单元的中间节点移到靠近裂纹尖端1/4位置处得到（1/4节点位移法），如图6所示［11-12］。20倾斜裂纹有限元模型如图7所示。

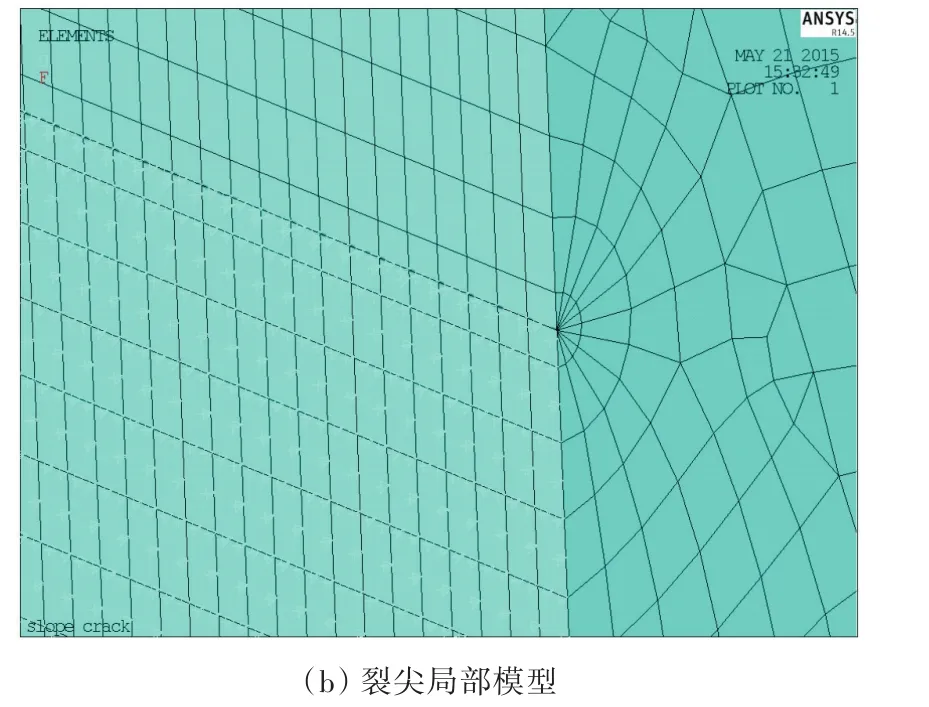
图7　SEN试件倾斜裂纹有限元模型Fig.7　FE model of SEN specimen with slant crack

采用1/4节点位移法计算应力强度因子的计算原理如式（6）所示：

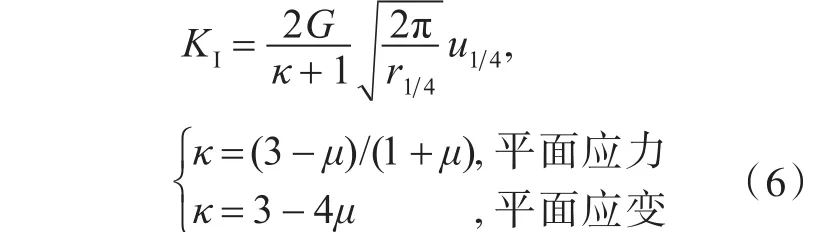
式中：G为剪切模量；μ为泊松比；r1 4为1/4节点距裂尖节点的距离；u1 4为1/4节点的张开位移。

在对三维裂纹进行线弹性分析，计算裂纹尖端应力强度因子K时，应事先假定裂纹尖端的应力状态，这样才能选择使用相应的计算公式。一般情况下，存在以下2种假设：

1）表面层假设：假设试件表面的应力状态为平面应力状态，在非表面位置为平面应变状态［13］。

2）假设试件沿厚度方向全部为平面应变状态［14］。实际上，在试件表面处，垂直于表面方向的变形不受约束作用，故试件表面上为双轴平面应力状态。可见表面层假设更为准确，因此，本文基于表面层假设来计算应力强度因子。

模型两自由表面为平面应力状态，使用Plane 183单元，非表面位置为平面应变状态，使用Solid 186单元，所加载荷为试验峰值载荷35 kN。将有限元分析得到的沿厚度分布的K除以标准FCGR试验中式（3）计算结果进行无量纲化，得到KFEM/Kcal分布结果，如图8所示。图8显示了应力强度因子沿平均深度为20 mm的倾斜裂纹、平直裂纹和曲线裂纹前缘的分布情况。

由图8结合图2～图4可知，在裂纹扩展过程中，出现了一部分裂纹生长速度大于另一部分裂纹生长速度的现象，且当最大疲劳载荷接近标准规定的最大疲劳载荷时，两侧裂纹长度差值达到最小，倾斜裂纹趋向于平直。根据线弹性断裂力学理论进行有限元分析，ΔK应与KFEM/Kcal具有相似的趋势。故生长迅速的裂纹前缘应力强度因子幅值ΔK明显低于生长缓慢部分的，在载荷比相同的情况下，不考虑厚度效应，生长迅速部分的裂纹扩展速率将会低于生长缓慢部分的，则裂纹前缘趋于平直。

显然，试件表面附近的应力强度因子到厚度中心区域有一个明显的突变区，这与Raju和Newman［15］在试验中获得的K分布及有限元计算结果出入较大，他们发现裂纹前缘沿其厚度方向应力强度因子值在板厚中心处大于表面处，因此，裂纹扩展速率在板厚中心处将大于表面处。这与图5的试件剖面结果一致，表明裂纹尖端区域线弹性应力强度因子的有限元分析计算在靠近结构表面处失真。故在下节中将对构件进行塑性分析以讨论裂纹前缘沿厚度方向的应力状态。

图8　不同裂纹尖端应力强度因子分布Fig.8　SIF for different crack front shapes

2.2塑性分析

上节所述线弹性分析忽略了应力状态对裂纹扩展过程中裂纹前缘的影响。本节在塑性分析的前提下计算裂纹尖端局部约束因子［16］，以验证应用表面层假设计算K值是否合理。

三维裂纹的坐标轴含义如图9所示。

图9　三维裂纹坐标轴方向Fig.9　Three-dimentional crack coordinate orientation

根据线弹性断裂力学理论，无限大平板I型中心裂纹双边受拉裂纹尖端附近应力场计算公式为：

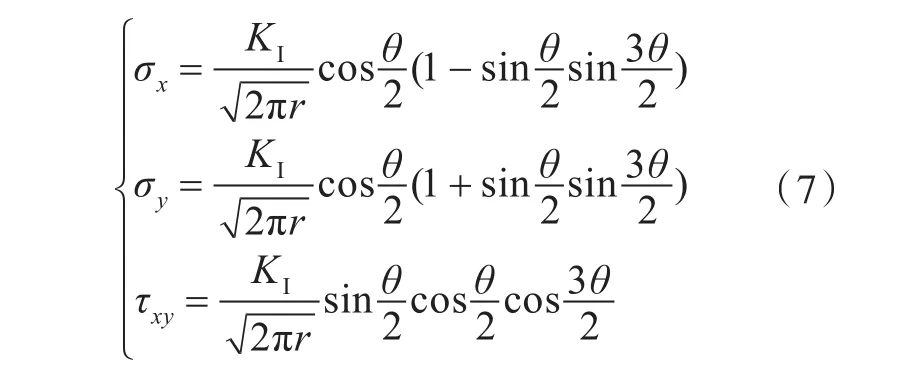
故裂纹尖端应力场的主应力分量分别为：

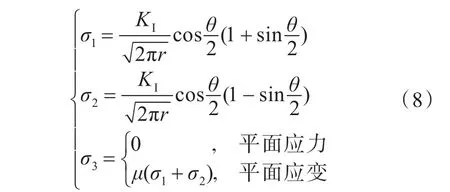
当θ=0时，主应力σ1=σ2=σ3=σy，根据Von-Mises屈服准则，塑性区屈服应力为

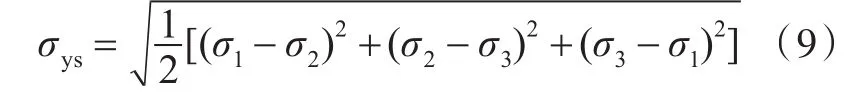
则容易得到：

式中：σx，σy，σz为沿坐标轴3个方向的应力；σ1，σ2，σ3为3个主应力；KΙ为I型裂纹应力强度因子；τxy为xy平面内的剪力；r为距裂尖距离；θ为与裂纹面夹角；σys为屈服应力；μ为泊松比，钢材取0.3。

由上式可知，理想状态下的平面应力和平面应变状态下的约束因子分别为1和3.3，而裂纹尖端区域的应力状态处于平面应力与平面应变状态之间，故αl⊂［1，3.3］。显然，裂纹前缘应力状态将沿厚度方向而改变。因此，本节使用局部约束因子概念以量化裂纹前缘平行于试件表面方向的应力状态，表达式如式（11）所示，符号含义如图10所示。

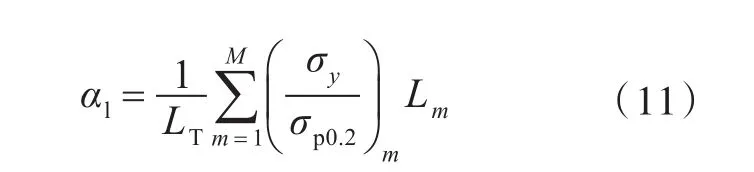
式中：LT为某一厚度位置在平行试件表面方向的塑性区尺寸；M为某一厚度位置在平行试件表面方向塑性尺寸内的节点个数；Lm为节点在平行试件表面方向所覆盖的尺寸。

在塑性分析阶段，有限元模型的网格划分和边界条件与弹性分析中相同，基于理想弹塑性假设，使用20节点六面体单元。计算参数如表4所示。

图11示出了不同裂纹深度模型的局部约束因子分布。由图可知，裂纹前缘局部约束因子具有以下分布特征：

图10　裂纹前缘塑性区尺寸形状Fig.10　Specifications of local constraint factor

表4　有限元模型参数Tab.4　Parameters for different FE models

图11　不同裂纹前缘局部约束因子分布Fig.11　Local constraint factor distribution for different models

1）含裂纹体厚板构件表面并不是理想的平面应力状态，而是随着裂纹深度的增加，有向平面应力状态转换的趋势；

2）厚度中心处的应力状态并非为理想的平面应变状态，而是随着厚度的增加，有向平面应变状态转换的趋势；

3）应力状态沿厚度方向从平面应力状态向平面应变状态转换的过渡区范围随着裂纹深度的增加而扩大。

图12所示为a=20 mm倾斜裂纹前缘局部约束因子的分布。由图可知，其裂纹前缘的应力状态很难被单纯地定义为平面应力状态（αl=1）或者平面应变状态（αl=3.3）。因此，在第2节的线弹性应力强度因子的有限元计算中所采用的表面层假设并不适用于裂纹深度为20 mm的厚板，其真实应力状态处于平面应变状态与平面应力状态之间。

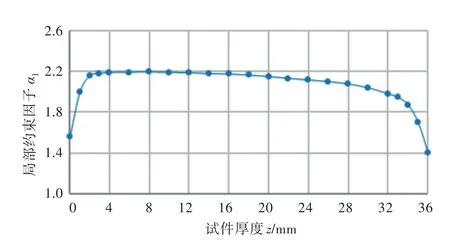
图12　20 mm倾斜裂纹前缘局部约束因子分布Fig.12　Local constraint factor distribution for slant crack model with depth of 20 mm

根据20 mm倾斜裂纹前缘局部约束因子的分布，可知倾斜裂纹的左半部分应力状态与右半部分相比更加趋向于平面应变，而平面应变状态下的三向应力会使裂纹体的脆性增加，故使得这部分的裂纹扩展速度相对于右半部分有所增加。通过对倾斜裂纹的线弹性有限元分析计算应力强度因子K和非线性有限元分析计算裂纹尖端局部约束因子αl，完整地解释了试验现象。

3　结　论

本文通过疲劳裂纹扩展速率试验对厚钢板裂纹尖端应力状态进行了试验研究，试验中观察到：

1）裂纹扩展速率在试件两侧面有明显的差异；

2）当最大疲劳载荷接近标准规定的最大疲劳载荷时，两侧裂纹长度差值达到最小，倾斜裂纹趋向于平直。

运用有限元方法，在线弹性分析的基础上对模型进行塑性分析，分别得到了裂纹尖端应力强度因子和局部约束因子沿试件厚度方向的分布情况，得到如下结论：

1）两侧裂纹长度差值在最大疲劳载荷接近标准规定的最大疲劳载荷时达到最小，裂纹平直度高，可为其他疲劳断裂试验中预制平直裂纹提供试验及理论依据；

2）裂纹扩展过程中的平直趋势用应力强度因子K或局部约束因子αl的分布均可进行分析；

3）沿板厚方向分布的裂纹尖端局部约束因子可有效量化裂纹尖端的应力状态分布。

4）本文将有限元分析模型的材料属性简化为理想弹塑性，忽略了循环载荷加载历史的影响，这些简化对结果的影响仍需要进一步研究。

［1］ABS.Guide for the fatigue assessment of offshore struc⁃tures［M］.Houston，TX：American Bureau of Ship⁃ping，2003.

［2］SCHIJVE J.Fatigue of structures and materials［M］. Heidelberg：Spring，2008.

［3］刘浩文.疲劳裂纹扩展的逻辑框架［J］.力学进展，1993，23（2）：269-286.

［4］LIU H W.A review of fatigue crack growth analyses ［J］.Theoretical and Applied Fracture Mechanics，1991，16（2）：91-108.

［5］COSTA J D M，FERREIRA J A M.Effect of stress ra⁃tio and specimen thickness on fatigue crack growth of CK45 steel［J］.Theoretical and Applied Fracture Me⁃chanics，1998，30（1）：65-73.

［6］WOLF E.Fatigue crack closure under cyclic tension ［J］.Engineering Fracture Mechanics，1970，2（1）：37-45.

［7］中国钢铁工业协会.金属材料疲劳裂纹扩展速率试验方法：GB/T 6398-2000［S］.北京：中国标准出版社，2001.

［8］SCHIJVE J.Four lecture on fatigue crack growth：Ⅰ. fatigue crack growth and fracture mechanics［J］.Engi⁃neering Fracture Mechanics，1977，11（1）：169-181.

［9］NEWMAN J C Jr，PHILLIPS E P，SWAIN M H.Fa⁃tigue-life prediction methodology using small-crack theory［J］.International Journal of Fatigue，1999，21 （2）：109-119.

［10］ 苗张木.厚钢板焊接接头韧度CTOD评定研究［D］.武汉：武汉理工大学，2005.

［11］BARSOUM R S.On the use of isoparametric finite ele⁃ments in linear fracture mechanics［J］.International JournalforNumericalMethodsinEngineering，1976，10（1）：25-37.

［12］HENSHELL R D，SHAW K G.Crack tip finite ele⁃ments are unnecessary［J］.International Journal for Numerical Methods in Engineering，1975，9（3）：495-507.

［13］LIN X B，SMITH R A.Finite element modeling of fa⁃tigue crack growth of surface cracked plates：part I：the numerical technique［J］.Engineering Fracture Mechanics，1999，63（5）：503-522.

［14］ GARCIA-MANRIQUE J，CAMAS D，LOPEZ-CRE⁃SPO P，et al.Stress intensity factor analysis of through thickness effects［J］.International Journal of Fatigue，2013，46：58-66.

［15］RAJU I S，NEWMAN J C，Jr.Three dimensional fi⁃nite element analysis of finite-thickness fracture spec⁃imen：NASA-TND-8414［R］.Hampton，VA：NASA Langley Research center 1977.

［16］董岩.疲劳裂纹扩展速率的厚度效应研究［D］.武汉：武汉理工大学，2014：33-36.

［17］NEWMAN J C，Jr，CREWS J H，BIGELOW C A，Jr，et al.Variations of a global constraint factor in cracked bodies under tension and bending loads：ASTM-TM-10119［R］.Hampton，VA：NASA Lang⁃ley Research Center，1994.

［18］NEWMAN J C，Jr.FASTRAN-Ⅱ：a fatigue crack growthstructuralanalysisprogram： NASA-TM-104159［R］.Hampton，VA：NASA Langley Research Center，1992.

Investigation on the stress state along the crack front in
the fatigue crack growth rate test for thick high strength steel plates

DANG Zhifan，YUE Jingxia，DONG Yan
School of Transportation，Wuhan University of Technology，Wuhan 430063，China

Complex environmental loads would unavoidably lead to the fatigue damage in marine struc⁃ tures，and the case worsens in high strength steel thick-welded structures which have typical tri-axial stress and the feature of brittleness.To study the stress state along the crack front，a standard fatigue crack growth rate test for high strength steel Q370QE with a thickness of 36 mm is conducted，and the correspond⁃ing material parameters and the threshold of stress intensity factor are obtained.Next，the abnormal behav⁃ior of a crack front during crack growth and the stress state along crack front during crack growth are ana⁃lyzed with the finite element method.Accordingly，the varying tendency of crack front shape could be quali⁃tatively defined.Finally，local constraint factors are introduced in order to quantitatively describe the stress state along the crack front with the growth of fatigue crack based on plasticity analysis，which provides prop⁃er explanation to why the crack front changes from slant to flat with the crack growing.The calculated stress intensity factor could only describe the stress state in the center area，but distortion is inevitable on the sur⁃face，while the local constraint factor can fully describe the stress state along the crack tip zone.

fatigue crack growth rate test；finite element analysis；stress state along the crack front；stress intensity factor；local constraint factor

U661.4

A

10.3969/j.issn.1673-3185.2016.02.008

2015-05-28网络出版时间：2016-3-17 10:56

国家自然科学基金资助项目（51009111）；中央高校基本科研业务费专项资金资助项目（135202006）

党之凡（通信作者），女，1991年生，硕士生。研究方向：结构安全性与可靠性。

E-mail：dangzhifan296@163.com

乐京霞，女，1977年生，博士，副教授。研究方向：结构安全性与可靠性。

E-mail：lejingxia@163.com