粒子群算法在求解数学建模最优化问题中的应用
2016-10-12王先超张开银孙娓娓王春生王志刚杨利峰
王先超, 韩 波,张开银, 孙娓娓, 王春生, 王志刚,杨利峰
(阜阳师范学院 a.数学与统计学院;b.计算机与信息工程学院;c.物理与电子工程学院;d.经济学院,安徽 阜阳,236037)
粒子群算法在求解数学建模最优化问题中的应用
王先超a, 韩波b,张开银c, 孙娓娓a, 王春生a, 王志刚a,杨利峰d
(阜阳师范学院 a.数学与统计学院;b.计算机与信息工程学院;c.物理与电子工程学院;d.经济学院,安徽 阜阳,236037)
最优化问题是数学建模常见问题之一。本文探讨了如何用群集智能算法粒子群算法求解最优化问题。并分别通过无约束和有约束条件的最优化问题实例来讨论用粒子群算法求解这类问题的一般步骤。结果显示PSO算法具有收敛速度快等优势。
粒子群算法;数学建模;局部最优解;全局最优解
作为联系数学与工业的重要桥梁,数学建模是数学走向应用的必经途径[1]。该项实践教学不仅可以提高学生分析和解决问题的能力,应用计算机及相关软件的能力,而且还可以提高学生用数学语言表达客观事物的能力、撰写科技论文的能力、创新能力和团结协作精神[2]。同时,数学建模实践教学也是大学生素质教育和能力培养的重要内容[3]。因而,越来越受到人们的普遍重视。
在实际建模过程中,经常对一些最优化问题进行求解。对于简单的优化问题如线性规划和整数规划可以用Lingo或Lindo[4]以及Matlab软件求解。对一些较复杂的非线性规划问题直接求解比较困难或为得到更优的解,需要使用现代智能优化算法,包括模拟退火算法(Simulated Annealing)[5]、遗传算法(Genetic Algorithms)[6]、人工神经网络(Artificial Neural Network)[7-8]、蚁群算法(AntColony Algorithms)[9]等。本文将重点讨论如何用粒子群算法(Particle Swarm Optimization,PSO)算法求解数学建模中的优化问题。
1 PSO算法简介
PSO算法是一类基于群体迭代的智能随机优化算法[10-15]。它是由Kennedy和Eberhart对鸟类的群体觅食行为进行建模和仿真结果中受到启发而提出的一种鲁棒性很强的仿生学优化算法[10-11]。目前PSO算法已广泛应用于神经网络训练[12-13]、模糊系统控制[14]以及其他的应用领域[15]。在PSO算法中,优化问题的每个可行解都是搜索空间中的一只鸟,称其为“粒子”。每个粒子都具有两个属性——位置和速度,分别表示其在解空间中的解和解的变化速度。PSO算法首先通过随机初始化一定数量的粒子(即随机解)构成粒子群,再利用迭代寻优和进化策略获得问题的最优解。每次迭代过程中以粒子位置对应的函数值,一般称其为适应度,确定粒子的优劣;每个粒子通过跟踪两个最优解——全局最优解和局部最优解——来进行位置和速度的更新。全局最优解是指粒子群全体当前寻找到的最优解,局部最优解是指单个粒子当前找到的最优解。
2 PSO算法求解最优化问题
本节将首先讨论用PSO算法求解最优化问题的一般步骤,而后通过两个实例来说明如何用PSO算法求解数学建模优化问题。
2.1用PSO算法求解最优化问题的一般步骤
假设目标搜索空间的维度为D,其中有N个粒子组成的群体,第i个粒子的位置用一个D维矢量Pi=(Pi1,Pi2,…,PiD)表示,且Pij∈[Pjmin,Pjmax],j= 1,…,D。
每个粒子的运动速度也用一个D维矢量Vi= (Vi1,Vi2,…,ViD)表示,且Vij∈[Vjmin,Vjmax],j=1,…,D。显然,每个粒子的位置就是搜索空间中的一个解,将其代入目标函数f而得到的函数值(在PSO算法中称其为适应度)可用于衡量解的优劣。用PSO算法求解最优化问题的一般步骤如下:
Step1:建立实际问题的数学模型,设其最优化函数为f。
Step2:种群初始化。产生一个包含N个粒子的粒子群,其位置和速度分别为Pi和Vi,i=1,…,N。
Step3:计算每个粒子的目标函数值f(Pi)。
Step4:根据函数值,计算全局最优值fgb和粒子位置D) 及每个粒子所经历过的最优值fdb和粒子位置
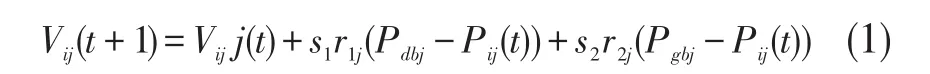
Step5:根据公式(1)和(2),分别对每个粒子的速度和位置进行更新。其中i=1,…,N,j=1,…,D,t为迭代次数,S1和S2为学习因子常数且非负,r1j和r2j为服从[0,1]上均匀分布且彼此独立的随机数。

Step6:判断是否满足终止条件。若满足则输出解,否则转至Step3。
算法具体流程图,如图1所示。

图1 PSO算法求解数学建模中最优化问题流程图
2.2用PSO算法求解无约束条件的最优化模型
下面通过一个实例来说明如何用PSO算法求解无约束条件的最优化问题。
2.2.1飞机定位问题
例1飞机在飞行过程中能够根据接收到地面上各控制台发来的飞机当前位置信息,比较精确地确定其位置,如图2所示。图中VOR1-3为3个高频多向导航设备,它们能够得到飞机与该设备连线的角度信息(以弧度表示);DME为距离测量装置,它能够得到飞机与该设备的距离信息(以km为单位)。已知4种设备的坐标(假设飞机与这些设备在同一平面),如何根据图中信息精确地确定飞机的当前位置?
2.2.2模型建立
设4种设备VOR1、VOR2、VOR3、DME的坐标分别为(xi,yi),当前飞机的位置为(x,y),VOR1、VOR2、VOR3测得的角度(从正北方向开始,沿顺时针方向的弧度)分别为αi(i=1,2,3)。DME测得的距离为d,根据数据计算的角度和距离分别为βi(i=1,2,3)和d4,则上述问题即为根据图2所给信息求(x,y)。
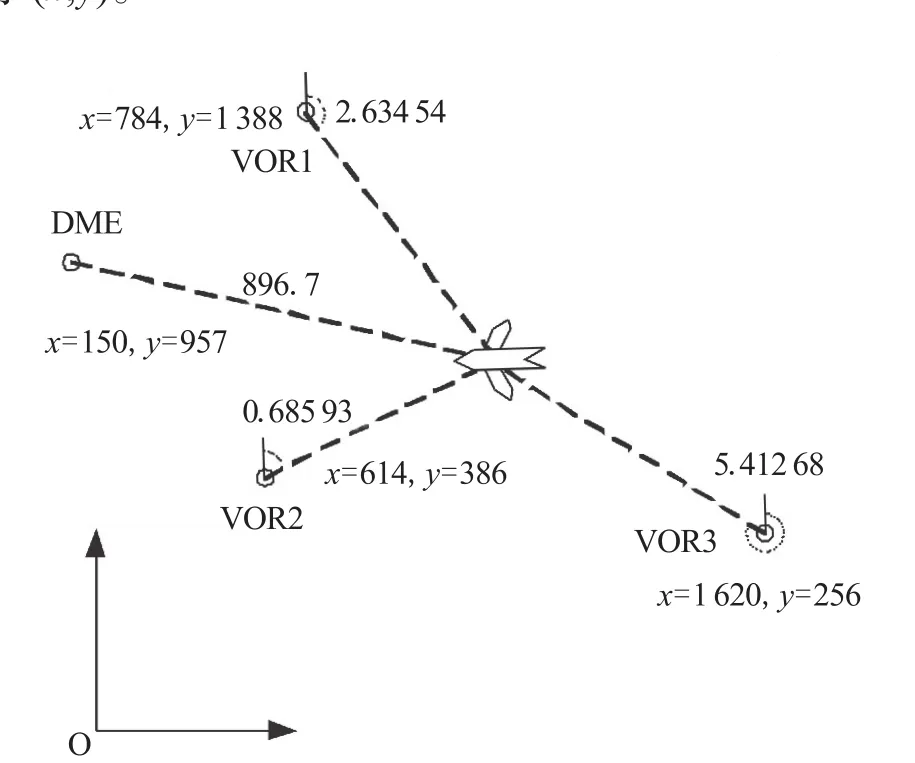
图2 飞机与各控制台位置信息图
对VOR设备,可以根据下面的公式(3)计算βi的正切值

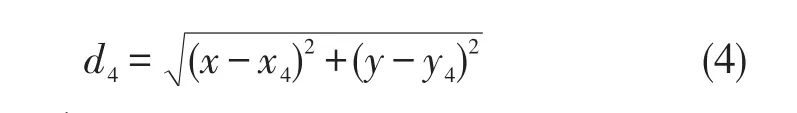
利用(3)和(4)确定飞机的位置坐标,即是在最小二乘准则下使计算值与测量值误差的平方和最小。因此,目标函数为
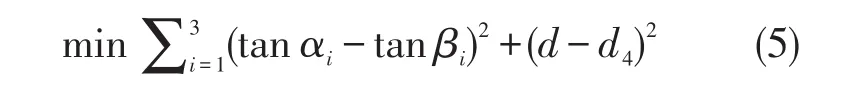
2.2.3模型求解
若使用Lingo软件求解该模型,可得其目标函数值为 71.085 17,飞机坐标为(277.291 4,69.051 59)。显然,它是一个局部最优解。若启动Lingo的“Use Global Solver”选项,可得目标函数的全局最优值为 0.058 167 08,飞机坐标为(1 037.831,831.198)。下面将根据图1所示的流程图重点讨论如何用PSO算法在Matlab平台对该模型进行求解。
(ⅱ )参数初始化
参数初始化包括两个学习因子s1和s2、进化次数Maxg、种群规模SizePop、初始速度上下边界值Vmax和Vmin和种群上下边界值Xmax、Xmin、Ymax和Ymin,并产生初始粒子位置Pop和速度V以及每个粒子的适应度Fitness,相关Matlab代码如下:

%随机产生一个粒子包括位置、速度和适应%度

其中fun函数根据(5)编写,其代码如下:

(ⅰ)最优位置初始化
最优位置是用粒子的适应度值来衡量的。如前所述,最优位置初始化包括每个粒子的最优解初始化和所有粒子最优解初始化,相关代码如下:

迭代寻优过程如下:首先运用公式(1)和(2)对每一个粒子的速度和位置进行更新,而后计算每个粒子的适应度值,再根据适应度值更新个体最优和全局最优;重复上述过程,直至迭代次数Maxg为0。相关Matlab代码如下:

用PSO算法求解该模型的运行结果:目标函数值为 0.058 167 13、飞机坐标为(1 037.82,831.12)。整个过程中适应度的变化如图3所示。可以看出收敛速度在迭代次数大概小于8次时很快,之后就比较慢,当迭代次数达到61次左右时适应度值基本不再改变。而上述用Lingo求解时迭代次数达到数万次。由此可见,用PSO算法求解最优化问题具有算法收敛速度快的优点。
2.3用PSO算法求解有约束条件的最优化模型
例2用PSO算法求解下面具有约束条件的非线性规律。
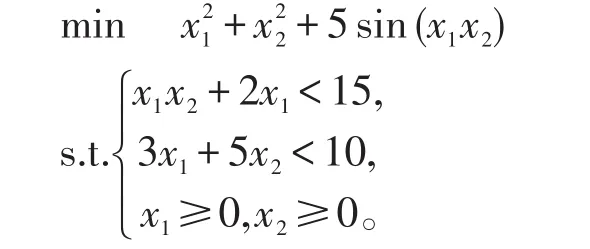
在例1的基础上,用PSO算法求解该问题时只需对上述代码稍作修改即可。需要修改的主要内容包括重新定义目标函数fun、种群的上下边界值、迭代寻优过程中适应度值Fitness的计算。

图3 用PSO算法求解飞机定位问题适应度值随迭代次数变化图
fun函数的定义如下:

根据约束条件,假设种群中变量x1和x2的上下边界相同均为20和0,即相关代码为Max=20;Min=0;将例1中适应度Fitness的计算代码Fitness(j)=fun (Pop(j,:));用下面带约束条件的代码替换

程序的运行结果为:当x1=0,x2=0时的目标函数值为0。由目标函数的图像图4可知,该结果为该非线性规划问题的全局最优解。当然,迭代次数和种群规模也可以修改。
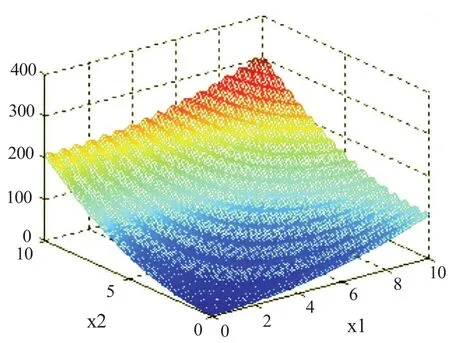
图4 的图像
3 小结
本文首先简单介绍了作为一种群集智能算法的PSO算法,而后通过两个具体实例说明如何使用它解决数学建模过程中经常遇到的最优化问题。从中可以看出PSO算法具有收敛速度快优势。收敛速度的快慢以及能否收敛于全局最优解主要取决于种群的规模。也就是说,为了得到全局最优解,种群的规模不能太小;否则,得到的可能是局部最优解。此外,本文讨论的PSO算法不能解决像TSP那样的离散最优化问题。要用PSO算法解决TSP等离散最优化问题需要对它进行改进,使其成为离散PSO算法。
[1] 李大潜.数学建模的教育是数学与工业间最重要的教育界面[J].数学建模及其应用,2012,1(1):38-41.
[2] 孙树东.数学建模融入大学数学相关实践分析[J].长春大学学报(自然科学版),2014,24(2):542-544.
[3] 李大潜.数学建模与素质教育[J].中国大学教学,2002(10):41-43.
[4] 谢金星,薛毅.优化建模与LINDO/LINGO软件[M].北京:清华大学出版社,2006.
[5] Wah B W,Chen Y X,Wang T.Simulated annealing with asymptotic convergence for nonlinear constrained optimization[J].Journal of Global Optimization,2007,39(1):1-37.
[6] Gopalakrishnan H,Kosanovic D.Operational planning of combined heat and power plants through genetic algorithms for mixed 0-1 nonlinear programming[J]. Computers&Operations Research,2015,56:51-67.
[7] Effati S,Ranjbar M.A novel recurrent nonlinear neural network for solving quadratic programming problems[J].Applied Mathematical Modelling,2011,35 (4):1688-1695.
[8] Nazemi A.A neural network model for solving convex quadratic programming problems with some applications[J].Engineering Applications of Artificial Intelligence,2014,32:54-62.
[9] Schlüter M,Egea J A,Banga J R.Extended ant colony optimization for non-convex mixed integer nonlinear programming[J].Computers&Operations Research,2009,36(7):2217-2229.
[10]Kennedy J,Eberhart R C.Particle swarm optimization [C]//Proceedings of IEEE International Conference on Neural Networks,1995:1942-1948.
[11]Eberhart R,Kennedy J.A new optimizer using particle swarm theory[C]//Micro Machine and Human Science,1995.MHS'95.,Proceedings of the Sixth International Symposium on.Nagoya,Japan,1995:39-43.
[12]Green I R,Wang L F,Alam M.Training neural networks using Central Force Optimization and Particle Swarm Optimization:Insights and comparisons[J].Expert Systems WithApplications,2012,39(1):555-563.
[13]Tsekouras G E,Tsimikas J.On training RBF neural networks using input-output fuzzy clustering and particle swarm optimization[J].Fuzzy Sets and Systems,2013,221:65-89.
[14]Siano P,Citro C.Designing fuzzy logic controllers for DC-DC converters using multi-objective particle swarm optimization[J].Electric Power Systems Research,2014,112:74-83.
[15]Cai Q,Gong M G,Ma L J,et al.Greedy discrete particle swarm optimization for large-scale social network clustering[J].Information Sciences,2015,316:503-516.
Application of particle swarm optimization to solve optimization problem in mathematics modeling
WANG Xian-chaoa,HAN Bob,ZHANG Kai-yinc,SUN Wei-weia,WANG Chun-shenga, WANG Zhi-ganga, YANG Li-fengd
(a.School of Mathematics and Statistics;b.School of Computer and Imformation Engineering;c.School of Physics and Electronic Engineering;d.School of Economics,Fuyang Normal University,Fuyang Anhui 236037,China)
Optimization problem is one of the common problems of mathematical modeling.This paper explores how to solve these problems by the use of the particle swarm optimization(PSO)algorithm.At the same time,it discusses the general steps to solve optimization problems by PSO,demonstrating two examples with unconstrained and constrained conditions,respectively.The results illustrate that PSO has the advantages such as fast convergence rate.
particle swarm optimization;mathematics modeling;locally optimal solution;globally optimal solution
G652
A
1004-4329(2016)02-117-05
10.14096/j.cnki.cn34-1069/n/1004-4329(2016)02-117-05
2015-08-20
安徽省教育厅自然科学研究重点项目(KJ2015A191,KJ2015A182);安徽省质量工程项目(2014zy138);阜阳师范学院质量工程项目(2013ZYSD05,2014JXTD01)资助。
王先超(1973-),男,博士,副教授,研究方向:光计算与数学建模。
