CdF分子基态和低激发态的多参考组态理论研究

赵书涛，丁海宁，周理想，武　山，张志国，王丽萍，吴言宁，张开银

（阜阳师范学院 物理与电子工程学院，安徽 阜阳 236037）

CdF分子基态和低激发态的多参考组态理论研究

赵书涛，丁海宁，周理想，武山，张志国，王丽萍，吴言宁，张开银

（阜阳师范学院 物理与电子工程学院，安徽 阜阳 236037）

采用含Davidson修正的多参考组态相互作用方法（MRCI+Q），对F原子和Cd原子分别使用相关一致基augcc-pVQZ和相对论赝势基aug-cc-pwCVQZ-PP，对CdF分子对应最低两个离解限Cd（1Sg）+F（2Pu）和Cd（3Pu）+F（2Pu）的14个电子态2Σ+（3），2Π（3），4Σ+（2），4Π（2），2，4Δ，2，4Σ-，在核间距R=1.3-6.0Å之间进行了Λ-S态势能曲线计算。理论计算结果表明，X2Σ+，22Σ+，22Π，32Σ+为束缚态，而12Π，32Π，12Σ-，12Δ，14Σ+，24Σ+，14Π，24Π，14Δ，14Σ-为排斥态，两个离解限能量间隔为30 147 cm-1。随后，依据Λ-S束缚态势能曲线，对X2Σ+，22Σ+和22Π进行了振动能级和转动常数的计算。上述计算结果跟已有的实验值比较接近。

CdF；势能曲线；振动能级；转动常数

Cd为IIB族元素，它的氟化物具有显著的生物毒性［1-3］，伴随着现代工业研究的不断发展，含有这类氟化物的废弃物通过各种渠道排放到人类的生活环境中，对人们的身体造成极大危害。检测这类氟化物的排放需要获得它们的精确光谱数据，然而，由于实验技术和理论方法的制约，相关的光谱数据非常少。

Zn为Cd的同族元素，它的氟化物自由基的实验和理论方面的研究较多。实验方面，Moravec 和Flory等人获得了ZnF自由基的X2Σ+态的结构和转动分辨的光谱常数［4，5］。Rochester和Olsson给出了 A2Π1/2和 A2Π3/2态的绝热激发能分别为4.586 eV和4.632 eV［6］。理论方面，Hayashi等人应用多参考组态相互作用（MRCI）方法结合相对论有效芯势（RECP）计算了ZnF自由基最低的两个离解限对应的全部Λ-S态的势能曲线，从理论上模拟出了较低几个束缚态的振动分辨的吸收谱［7］。Leonard等人采用纳入自旋-轨道耦合效应的MRCI方法计算了最低的两个离解限对应的Λ-S态和Ω态的电子结构，讨论了电子态之间的自旋-轨道耦合作用导致的A2Π态的预解离现象［8］。与含有Zn原子的氟化物自由基相比，近些年关于含有Cd原子的氟化物自由基的实验和理论研究相对较少，赫兹堡等人［9］总结了早期研究给出Cd的氟化物自由基的电子态光谱数据。由于受到早期实验条件的制约，这些自由基的基态和激发态的光谱数据均不完备。近年来，关于含Cd原子的氟化物自由基的理论数据非常少，目前还没有相关的理论文献。不过，作为Cd的最简单化合物，它的氢化物的研究较多［10-12］，对较低离解限的Λ-S和Ω态进行了计算，表明对含Cd原子的自由基的理论研究正在兴起。本文对Cd的卤化物自由基CdF的基态和较低激发态进行高精度的从头算，计算中未考虑自旋-轨道耦合效应，只对最低两个离解通道的Λ-S态进行计算。

采用MRCI方法和相关一致基aug-cc-pVQZ （F原子）［13］及相对论赝势基aug-cc-pwCVQZ-PP （Cd原子）［14］，在Molpro程序下计算CdF分子对应于最低两个解离通道的Λ-S态势能曲线。利用这些势能曲线的计算结果，借助LEVEL程序求解Schrödinger方程，得到束缚Λ-S态的光谱参数。

1　计算方法

对于较大的双原子分子CdF，要得到它的精确的势能曲线就必须采用多参考组态相互作用（MRCI）理论进行准确的相关能计算。本文采用MRCI方法在MOLPRO2010［15］程序下进行了势能曲线的精确计算。计算过程中，F原子采用了相关一致基aug-cc-pVQZ，对于电子数较多的Cd原子，出于目前实验室计算硬件的限制，则使用了相对 论 赝 势 基 组 aug-cc-pwCVQZ-PP（Cd：ECP28MDF）。

在势能曲线的计算中，MRCI方法只能使用Abelian点群。CdF分子的对称性为C∞v群，然而，由于程序的局限，计算中必须由C2v群代替。C2v群的不可约表示为A1，B1，B2，A2，和C∞v群有以下对应关系：Σ+=A1，Π=B1+B2，Δ=A1+A2和Σ-=A2。在1.3～6.0Å之间给定的核间距上，采用Hartree-Fock（HF）自洽场方法获得了CdF分子基态的分子轨道，以此为初始波函数，采用完全活性空间自洽场（CASSCF）方法对波函数进一步优化。我们选取F原子的2p和Cd原子的5s5p价壳层对应的分子轨道作为CASSCF计算的活性空间轨道。随后，以CASSCF波函数为参考，考虑Davidson修正，利用MRCI方法计算了14个Λ-S态的本征能量。在MRCI计算中，由于Cd原子采用相对论赝 势 基aug-cc-pwCVQZ-PP，冻 结 了1s22s22p63s23p63d10电子，故F原子的1s2和Cd原子的4s24p6电子被放入内核轨道，而F原子的2s2和Cd原子的4d10电子作为关联电子。这样，F原子的2s2和Cd原子的4d10电子的内壳层-价壳层电子关联被考虑进来，在MRCI计算中CdF分子的19个电子的关联效应被考虑进来。

最后，在Λ-S态势能曲线的计算结果上，利用LEVEL［16］程序数值积分来求解CdF分子的一维核运动Schrödinger方程，得到相关束缚态的振动能级和转动常数。

2　研究结果

2.1离解限和电子态

F原子的基电子组态为1s22s22p5，对应的谱项为2Pu，Cd原子的最低两个电子态为［Kr］4d105s2和［Kr］4d105s5p，对应的谱项为1Sg和3Pu，1Pu。由美国国家标准与技术研究院（NIST）的数据可知对应CdF分子的最低2个离解限为Cd（1Sg）+F（2Pu）和Cd（3Pu）+F（2Pu）。Cd（1Pu）+F（2Pu）是CdF分子更高的离解通道，考虑此通道对应的分子态，计算量将增大。鉴于目前的计算条件，本文只涉及最低的两个离解通道对应分子态的理论计算。

F、Cd原子的原子态和CdF分子的分子态所属点群分别为SO（3）和C∞v，它们的不可约表示对应关系为Sg→Σ+，Pu→Σ++Π。当Cd（1Sg）原子和F （2Pu）原子形成CdF分子时对称性降低，SO（3）群的不可约表示分解为C∞v的不可约表示的直和，再通过直积得到对应分子的可能的电子态。通过式（1），可以得到第一离解限Cd（1Sg）+F（2Pu）对应的电子态为2Σ+和2Π。进一步通过式（2），可以得到第二离解限 Cd（3Pu）+F（2Pu）对应的电子态为2，4Σ+（2），2，4Σ-，2，4Π（2）和2，4Δ。

对CdF分子电子态的MRCI势能曲线的计算就按照上述两个离解极限进行，其中涉及二重态的有8个：2Σ+（3），2Π（3），2Σ-，2Δ；四重态的有6个：4Σ+（2），4Π（2），4Σ-，4Δ。Λ-S态与离解限的关联表及计算结果见表1。

表1　Λ-S态与解离限关联表

从表1中可以看出，14个Λ-S态对应的两个离解限间距的计算结果30 147 cm-1跟NIST给出的实验值［17］31 246 cm-1比较接近，偏差为1 099 cm-1，这为本文后续的理论计算提供可靠的基础。

2.2势能曲线

在MRCI+Q方法下对Cd（1Sg）+F（2Pu）和Cd （3Pu）+F（2Pu）两个离解限对应的14个Λ-S态进行了势能曲线的扫描计算，结果如图1和2所示，其中图1为二重态势能曲线，图2为四重态势能曲线。

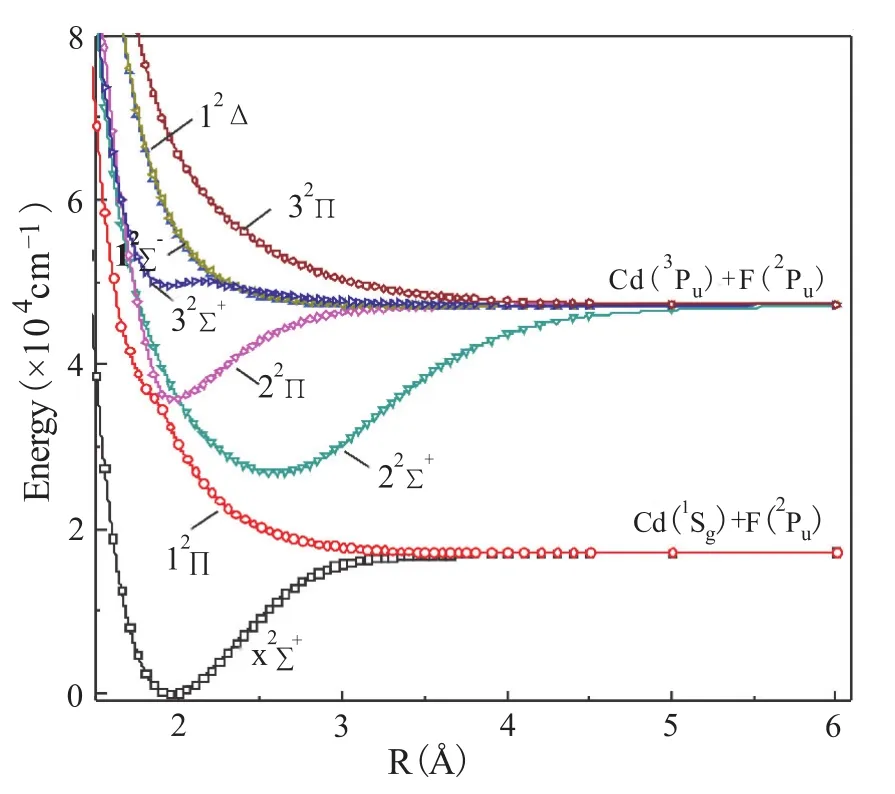
图1　MRCI+Q计算的CdF分子的二重态势能曲线

从图中可以看出，X2Σ+，22Σ+，22Π，32Σ+为束缚态，而12Π，32Π，12Σ-，12Δ，14Σ+，24Σ+，14Π，24Π，14Δ，14Σ-为排斥态。基态X2Σ+的平衡位置在R=1.95 Å附近，在核间距R=2.60 Å处与相同对称性的激发态22Σ+有强烈的相互作用。22Σ+和32Σ+对应于离解限Cd（3Pu）+F（2Pu），由于相同对称性的避免交叉，22Σ+态有一个深势阱，在R=2.60 Å处有极小值，32Σ+有一个很浅的势阱，只能容纳1个振动能级，在R=1.95 Å处有极小值。由于相同的对称性，12Π和22Π在R=1.90 Å附近发生避免交叉，导致两态分别对应于离解限Cd（1Sg）+F（2Pu）和Cd（3Pu）+F （2Pu）。由于避免交叉现象，22Π有一个较深的势阱，在R=1.95 Å处有极小值。

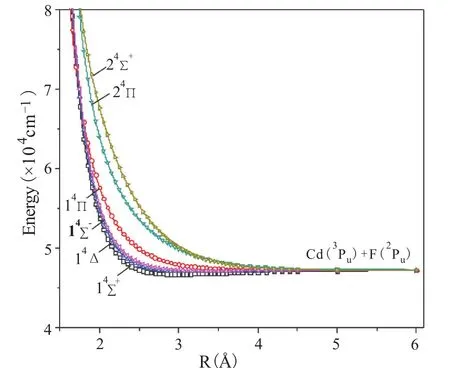
图2　MRCI+Q计算的CdF分子四重态势能曲线

在基态X2Σ+的平衡位置R=1.95 Å处给出了较低的Λ-S态X2Σ+，12Π，22Π，22Σ+，32Σ+和12Σ-的垂直激发能和主要组态。12Π，22Π和22Σ+的分布在32 000～38 000 cm-1区间，相互作用较强。12Π，22Π，22Σ+，32Σ+和 12Σ-的主要组态分别为6σ27σ28σ03π34π0，6σ27σ08σ03π44π1，6σ17σ28σ03π44π0，6σ27σ08σ13π44π0和 6σ27σ18σ03π34π1分别对应于3π→7σ，7σ→4π，6σ→7σ，7σ→8σ和3π→4π单电子跃迁。

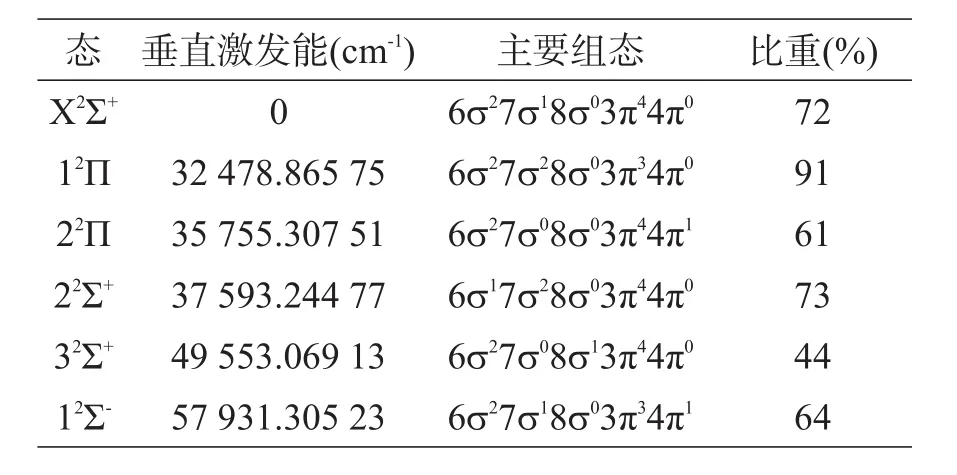
表2　较低Λ-S态的垂直激发能和主要组态R=1.95 Å

2.3振动能级和转动常数

在Λ-S态势能曲线基础上，通过LEVEL程序求解CdF核运动的薛定谔方程，得到了X2Σ+，22Σ+和22Π的振动能级和转动常数。对应上述3个束缚态分别找到49，91和32个振动能级，鉴于篇幅限制，只给出了前32个振动能级。

表3　X2Σ+，22Σ+和22Π的振动能级G（v）和转动常数Bv

3　结论

采用MRCI+Q方法对CdF分子对应于Cd （1Sg）+F（2Pu）和Cd（3Pu）+F（2Pu）离解限的14个电子态2Σ+（3），2Π（3），4Σ+（2），4Π（2），2，4Δ，2，4Σ-，进行了高精度的从头计算。两个离解限能量间隔为30 147 cm-1与实验结果符合良好，X2Σ+，22Σ+，22Π，32Σ+为束缚态，而其它10个态（12Π，32Π，12Σ-，12Δ，14Σ+， 24Σ+，14Π，24Π，14Δ，14Σ-）均为排斥态，预测的X2Σ+，22Σ+和22Π的振动能级和转动常数可为后续的实验和理论研究提供重要参考。

［1］ Koren Š，Arčon I，Kump P，et al.Influence of CdCl2 and CdSO4 supplementation on Cd distribution and li-gand environment in leaves of the Cd hyperaccumulator Noccaea（Thlaspi）praecox［J］.Plant and Soil，2013，370（1/2）：125-148.

［2］ Meyer C L，Juraniec M，Huguet S A，et al.Intraspecific variability of Cadmium tolerance and accumulation，and cadmium-induced cell wall modifications in the metal hyperaccumulator Arabidopsis halleri［J］.Journal of Experimental Botany，2015，66（11）：3215-3227.

［3］Isaure M P，Huguet S，Meyer C，et al.Evidence of various mechanisms of Cd sequestration in the hyperaccumulator Arabidopsis halleri，the non-accumulator Arabidopsis lyrata，and their progenies by combined synchrotron-based techniques［J］.Journal of Experimental Botany，2015，66（11）：3201-3214.

［4］ Moravec V D，Klopcic S A，Chatterjee B，et al.The electronic structure of ZnO and ZnF determined by anion photoelectron spectroscopy［J］.Chemical Physics Letters，2001，341（3/4）：313-318.

［5］ Flory M A，Mclamarrah S K，Ziurys L M.Completing the 3d metal fluoride series：The pure rotational spectrum of ZnF（X-2 Sigma（+））［J］.Journal of Chemical Physics，2006，125（19）：194304-194309.

［6］ Rochester G，Olsson E.Das bandenspektrum des MnF ［J］.Zeitschrift für Physik，1939，114（7/8）：495-499.

［7］ Hayashi S，Leonard C，Chambaud G.Ab initio study of the low lying electronic states of ZnF and ZnF-［J］. The Journal of Chemical Physics，2008，129（4）：044313.

［8］Leonard C，Le Quere F.Theoretical study of the predissociation of the A（2）Pi state of ZnF including quasi-diabatisation of the spin-orbit coupling［J］.Journal of Chemical Physics，2012，137（16）：164318.

［9］Huber K，Herzberg G.IV of molecular spectra and molecular structure［M］.New York：Van Nostrand Reinhold，1979.

［10］Li Rui，Zhai Zhen，Zhang Xiaomei，et al.Spin-orbit all-electron configuration interaction study on the electronic structure and radiative lifetimes of low-lying excited states of CdH［J］.Chemical Physics Letters，2014，599：51-56.

［11］Zhang Xiaomei，Liang Guiying，Li Rui，et al.Multireference configuration interaction study on the potential energy curves and radiative lifetimes of low-lying excited states of CdH+cation［J］.Chemical Physics，2014，443：142-148.

［12］Abe M，Kajita M，Hada M，et al.Ab initio study on vibrational dipole moments of XH+molecular ions：X= 24Mg，40Ca，64Zn，88Sr，114Cd，138Ba，174Yband 202Hg［J］.Journal of Physics B-Atomic Molecular and Optical Physics，2010，43（24）：245102-245112.

［13］Dunning J H.Gaussian basis sets for use in correlated molecular calculations.I.The atoms Boron through Neon and Hydrogen［J］.The Journal of Chemical Physics，1989，90（2）：1007-1023.

［14］Peterson K A，Puzzarini C.Systematically convergent basis sets for transition metals.II.Pseudopotentialbased correlation consistent basis sets for the group 11 （Cu，Ag，Au）and 12（Zn，Cd，Hg）elements［J］.Theoretical ChemistryAccounts，2005，114（4/5）：283-296.

［15］Werner H J，Knowles P J，Lindh R，et al.MOLPRO，A package of ab initio programs［Z］，2010.

［16］Le Roy R J.LEVEL 8.0 A computer program for solving the radial Schrödinger equation for bound and quasibound levels，University of Waterloo：Chemical Physics Research Report NO.CP-663，2007.

［17］ Burns K，Adams K B.Energy levels and wavelengths of natural cadmium and of cadmium-114［J］.Journal of the Optical Society ofAmerica，1956，46（2）：94-99.

MRCI calculations for ground and excited states of CdF molecule

ZHAO Shu-tao，DING Hai-ning，ZHOU Li-xiang，WU Shan，ZHANG Zhi-guo，WANG Liping，WU Yan-ning，ZHANG Kai-yin

（School of Physics and Electronic Engineering，Fuyang Normal University，Fuyang Anhui 236037，China）

The potential energy curves（PECs）of CdF correlating to the first two dissociation asymptotes Cd（1Sg）+F（2Pu）and Cd（3Pu）+F（2Pu）were computed by using multi-reference configuration interaction including Davidson correction（MRCI+Q）approach.The PECs of the fourteen states（2Σ+（3），2Π（3），4Σ+（2），4Π（2），2，4Δ，and2，4Σ-）were calculated in the internuclear distance range from 1.3 to 6.0 angstrom at the basis sets，aug-cc-pVQZ for F and aug-cc-pwCVQZ-PP for Cd atom.The calculated results show that X2Σ+，22Σ+，22Π，32Σ+are bound，while 12Π，32Π，12Σ-，12Δ，14Σ+，24Σ+，14Π，24Π，14Δ，14Σ-are repulsive.The energy gap of the second and the first dissociation limit is 30 147 cm-1.Based on the computed PECs of X2Σ+，22Σ+and 22Π，the vibrational level and rotational constant were obtained，which are in good accordance with the available experimental data.

CdF；potential energy curves；vibrational levels；rotational constants

O561

A

1004-4329（2016）02-028-05

10.14096/j.cnki.cn34-1069/n/1004-4329（2016）02-028-05

2016-02-10

安徽省教育厅项目（2014KJ020）；安徽自然科学基金项目（1608085MA10）；安徽省大学生创新训练项目（AH201410371076）；阜阳师范学院科研项目（2014FSKJ04ZD）资助。

赵书涛（1982－），男，博士，讲师，研究方向：原子与分子物理、光学。