多电平高压级联Boost直流变换器研究
2016-10-12刘闯李航孙洲同蔡国伟
刘闯,李航,孙洲同,蔡国伟
(1.东北电力大学 电气工程学院,吉林 吉林 132012;2.哈尔滨供电局,黑龙江 哈尔滨 150001)
多电平高压级联Boost直流变换器研究
刘闯1,李航1,孙洲同2,蔡国伟1
(1.东北电力大学 电气工程学院,吉林 吉林 132012;2.哈尔滨供电局,黑龙江 哈尔滨 150001)
提出一种基于三电平结构的多电平级联Boost直流变换器,采用模块化及相应载波移相调制技术,使该变换器可以灵活用于高频隔离型高压直流变换器前端及高频隔离型高压PFC中间级。基本的三电平模块是由P-cell,N-cell单元构造而成,并且能够提供2个相同输出电压同时获得1倍于开关频率的等效频率。首先详细分析了多电平级联Boost DC-DC变换器在载波移相调制下的电路工作原理及电感电流与电容电压波纹特性,并讨论出不同占空比下的输入输出电压关系以及电感电流的趋势。最后,搭建功率5.3 kW的实验装置来验证多电平级联Boost变换器的工作特性。
多电平级联Boost变换器;高压直流变换器;高压PFC;电感电流波纹;电容电压波纹
电力电子变压器被认为是未来智能电网的重要组成部分,是通过电力电子和高频隔离技术来完成中压交流网与低压交流网之间的电能变换,可以实现传统变压器电压等级转换和隔离功能,同时可以抑制电网电压跌落和频率变化对负载侧的影响并隔离来自负载侧的无功电流和谐波对电网的污染。典型的电力电子变压器系统一般包含3个基本功率变换过程,分别为:1)中压工频交流到中压直流的AC-DC功率变换过程;2)中压直流到低压直流的DC-DC功率变换过程,实现了高频隔离、能量传递和降压的功能;3)低压直流到低压交流的DC-AC功率变换过程,来满足不同类型负载的要求[1-2]。其中第1个变换过程被称之为有源前端变换器整流(AFEC)部分,传统意义上的整流部分是采用不控整流加Boost变换器,结构简单,在常见的升压场合广泛应用,但系统在高升压变化需求时,基本的Boost一方面会降低系统的整体效率,另一方面当占空比较大时输出的电压不易升高。
针对此类问题目前提出了许多具有高升压功能的变换器拓扑结构,文献[3]提出的一种7电平级联变换器,一定程度上可以得到更好的输出波形,相对控制简单,但由于采用2H桥结构使得可控功率管数量增加,增加了系统的成本;文献[4]对级联多电平变换器最大输出电平数与波形质量、直流电压等级、模块单元数量等多个元素之间的关系进行了研究,但并没有具体分析模块级联对电感电流波纹和输出电压波纹的影响。文献[5]提出一种基于CDM单元的变换器,降低了开关管电压应力,解决了均流问题,但在更高电压、功率场合上的应用存在问题,同时系统结构整体依赖性强,不够灵活。
本文基于Boost的三电平电路对其进行级联,分析了级联型多电平Boost电路具体工作方式、原理[6-8]。具有以下优点:1)在平均载波移相控制方式下,探讨电感波纹与占空比之间的函数关系,减小了输入电流的纹波,从而降低了滤波设备的体积;2)分析了不同数量的模块级联时输出电压波形特性,使得输出电压纹波进一步减小,从而使得输出的波形质量更高;3)采用级联结构可以从容应对大功率、高电压场合,并且级联结构简易,每个模块可以灵活拆卸安装;4)应用在智能直流配电系统中,能够对低压直流母线电压进行调节控制,达到中压交流网与低压直流网之间的功率相互变换。
1 基本模块及工作原理
升压电路的拓扑从结构上可以分为P-cell和N-cell 2个基本开关模块,如图1所示。P-cell和N-cell互为镜像关系,区别在于相对于公共端N而言电流是流出的还是流入的[9-11]。根据Boost电路工作原理,若设主动开关管S的占空比为d则有以下公式:
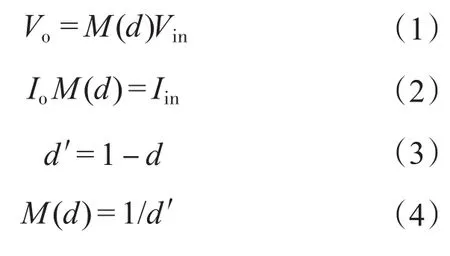

图1 P-cell、N-cell拓扑结构图Fig.1 The topology of P-cell and N-cell
其中,Vin,Vo,Iin,Io如图1所示,可以看到正是由于开关状态变化,使得电容电感之间不断充放电,即电感中流过的电流和电容两端电压,都存在着波纹。图2所示为Boost电路在稳定状态下,电感电流和电容电压波纹。

图2 Boost电路稳定状态下电感电流、电容电压波纹Fig.2 The inductor′s current and capacitor′s voltage ripple of boost converter under steady state
针对本文工作在CCM模式下的Boost电路[12],电感能量计算公式如下:

其中,ΔWLC为一个开关周期(cycle)电感能量变化,分别为输入电源对其注入能量ΔWLi和电感向负载输出能量ΔWLo,即:

式中:TS为主动开关管S开关周期时间。
从式(5)~式(7)中可以看出电路工作在稳定状态时能量达到守恒,即ΔWLC为0,ΔWLi和ΔWLo相等。可以看出,当Vo和Vin关系如式(1)所示时,满足ΔWLi和ΔWLo相等的稳定条件,此时电路达到稳定。另一方面,电容同样具备上述能量公式,如下:

当主动开关管开关S占空比决定了电容开关周期内能量变化,也就决定了电容两端输出电压大小。反过来电容两端输出电压又决定了电感开关周期内能量变化和输入电流的大小。在占空比确定后,可以确定Boost电路的输出电压,就是由于主动开关管和二极管切换电路,而电感电容在这种切换下,电感电流和电容电压相互影响,达到一种能量上的平衡。而代表能量过程的电感电流和电容电压波纹峰峰值计算如下:

在建立平衡后,电感和电容的波纹应该尽量减小,保证电能质量。一般需要控制波纹在平均值的5%~10%以内。而当输入电压过大时,由于电感上能量变化幅度大,就要求应用更大电感值的电感,使整个电路体积增大,同时也降低了系统的响应速度。而采取级联式多电平结构,加上PWM载波移向调制技术,可以在保持较低开关频率下有效解决上述问题。
2 三电平结构及其载波移相调制
2.1三电平结构原理分析
三电平单模块拓扑是级联型多电平Boost结构的基本单元,由图3可以看出三电平拓扑是由上文提及的P-cell,N-Cell串联构成的。电流流入时流经N-cell,电流流出时流经P-cell。为了承担高等级电压,需要将三电平单模块进行级联,因而模块的单独设计可以使得整个级联体系构造更便捷,每个模块在输入侧为串联连接从而适应了不同电压等级的直流源,输出侧为并联结构提供相同的输出电压。

图3 三电平模块拓扑结构Fig.3 The topology of 3-level boost converter
上述三电平结构,分为4种工作状态,如图4所示,分别为S1,S2都关断,S1导通S2关断,S2导通S1关断和两开关管均导通4种情况。
从图4中可以看出,主动开关管S1,S2决定电容C1,C2充放电过程。当S1断开,电容C1充电,当S1闭合,电容C1放电;当S2断开,电容C2充电,当S2闭合,电容C2放电。设定输出端所连接负载相等,设两输出电压分别为Vo1和Vo2,两输出电流为Io1和Io2,输入电压和电流分别为Vin和Iin,2个主动开关管占空比均为d,在3电平结构达到稳态时,针对电容充放电过程有以下公式:

其中,Iox指的是Io1,Io2中的任意1个,当两输出端负载相同,输出功率平衡,可以看出2个输出电压Vo1和Vo2的大小由开关管S1,S2的占空比来决定的,改变占空比的大小能得到不同的输出电压,实现Boost的工作原理。

图4 三电平模块拓扑结构4种工作状态Fig.4 Four operating state of 3-level module topology
2.2应用载波移相调制分析
电感上波纹过大会影响系统的整体效率,对后级系统也会造成一定的影响,为了减小电感波纹,采用载波移相调制即应用PWM技术生成两主动开关管触发信号时,将2个载波移相使二者相角相差180°,在1个开关周期中平均分配电感的2次充放电过程,以此提高了电感频率减小电感波纹,而这样的平均分配也避免了输出电压不平衡的出现。
如图5所示即为所述三电平结构在载波180°移相调制下,电容电压波纹、开关管触发信号和电感电流波纹的波形图。图5中所标明的数字0 到3和图4中的工作状态相对应。可以看到电容波纹频率即为开关频率;而在占空比不等于0.5的情况下,电感波纹频率为开关频率的2倍;在占空比等于0.5的情况下,电感波纹由于载波移相调制方式,降低到可以忽略的程度。
具体电容电压波纹和电感电流波纹计算公式如下:

对式(16)求导

不难发现二者的极大值点分别在d=0.25和d=0.75处取得,且二者极值相等。在设计三电平结构中的电感时,应考虑d在0.25或0.75处的电感波纹,使其满足电能质量要求。

图5 载波180°移相调制下电容电压波纹及电感电流波纹Fig.5 Capacitor voltage ripple and inductor current ripple under 180°shift-carrier waves
3 级联型多电平拓扑结构分析
3.1级联型多电平拓扑原理分析
为了应用于更高电压等级,进一步增加电感电流波纹等效频率,可以将三电平结构进行级联,在开关频率固定的情况下,每级联1个三电平结构,将会使得电感电流波纹等效频率在数值上以2倍开关频率增大。
当假设串联的三电平结构模块数为n,开关管开关频率为fS则电感电流波纹等效频率为nfS。随着串联模块的增加,移相控制则要相应地减小各载波移相角,使得输出侧充放电均匀分布。如图6为2个三电平模块结构串联,针对这种拓扑结构采用移相调制技术时,需要考虑能量平均分配问题,所以移相角应为90°,即在1个开关周期内对电感进行4次充放电过程[14-15]。

图6 两模块级联型三电平拓扑结构Fig.6 Three level topology of two modules cascade
同样可以根据能量平衡原理来推出输入电压、输出电压和各开关占空比的关系,单个开关周期,电容Ck能量变化公式依然与式(8)相类似,即
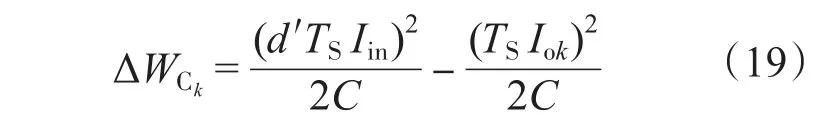
式中:Iok为k路输出电流。
而电感能量变化与前文所述有些不同,由于电感两端电压变化在各个开关管动作时都会产生变化,且作用于电感的输出电压也在不断切换。单个开关周期电感能量变化公式为

式中:n为单模块三电平结构级联数;Vok为第k路输出电压。
三电平级联拓扑结构在平均移相调制、各开关管占空比和各输出功率相等的条件下,通过能量平衡的建立,电感电流与输出电流,输入电压与各输出电压和之间的关系,依然如Boost电路公式,即有:
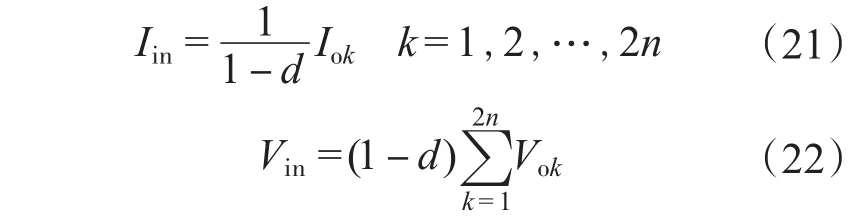
从各个单独的输出口来看,在输出电压方面其波纹及分析过程与Boost电路无异,而比较不同的是电感波纹的分析,这也是级联三电平拓扑结构的关键问题。
3.2特殊占空比下结构的运行特点
针对多电平的级联结构,均存在一些特殊的占空比,当各输出功率相同的前提下,在这些开关占空比下工作将使得级联多电平拓扑结构输入电流的波纹接近为0,这些特殊占空比分别为k/2n(k=0,2,…,2n)。并且在以这些特殊占空比为节点划分出的不同区域里,电感电流波纹的表现是一致的。本章以2个三电平结构级联后构成的电路为例,来分析多电平级联结构的工作原理和运行特点。
如表1所示,2个模块级联为在特殊节点处,占空比、开关状态和电感两端电压之间的关系表。在输出电压平衡状态下的特殊节点处,是因为应用式(22)得到Vin的值,此时由于输入输出电压等级一致,电感两端电压为0。

表1 两模块级联结构特殊节点状态表Tab.1 Special node status in two modules cascade structure
通过表1对特殊节点的分析,可以得出结论:在特殊节点处,输出端电容接入的数量等于(1-d)·2n。其中n依然为级联三电平模块数。以两模块级联三电平拓扑结构的1/4到2/4区间来说,电路不断在特殊节点1/4,2/4时的等值电路之间切换。而输入电压等级介于2Vok和3Vok之间,而接入输入端的输出电压在2Vok和3Vok之间切换,这就导致拓扑结构中的电感两端电压正负间切换,产生电感电流波纹。电感电流波纹计算公式为

式(23)中,电感电流波纹关于占空比d和模块数n的函数图形如图7所示。从图7中可以看出,随着占空比在0到1之间变化电感电流波纹存在多个极大值点和0点。随着模块级联数n成比例增加,电流波纹极大值等比例减小,极大值个数等比例增加。通过本章对两模块级联拓扑的研究,分析了多种电路状态,并推导出电感波纹和各电气量之间关系式,能够通用到任意多模块级联拓扑结构。

图7 电感电流波纹与模块数n占空比d关系图Fig.7 The relationship between inductance current ripple and the number of modules and the duty cycle
3.3开关管的稳态电压应力
通过表中的等效电路也可以看出,如果忽略二极管和功率管自身的导通压降,单模块时功率管开关电压应力为
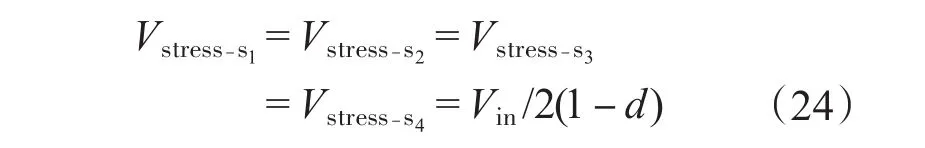
而二极管承受的最大电压应力同样为Vin/2· (1-d);当两模块级联时每个功率开关管的电压应力为
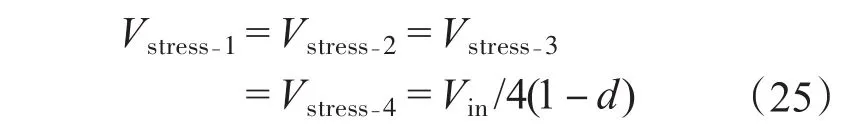
二极管的最大电压应力为Vin/4(1-d)。通过式(24)、式(25)分析可知每个功率开关管电压应力即为对应的输出电压,因此对于级联模块导通和关断过程中功率管和二极管的电压在0~Vin/ 2n(1-d)波动,其中n为级联模块数,与传统的Boost变换器相比降低了功率开关的电压应力。
4 仿真

图8 单个模块在d=0.75,0.5,0.25时电感电流及各电容电压波形Fig.8 Single module′inductive current and capacitor voltage waveforms in d=0.75,0.5,0.25
如图8~图10所示,分别为单个三电平模块、2个三电平模块级联和3个三电平模块级联结构,在各输出电压(450 V)及输出功率(10 kW)相同情况下,不同占空比下的电感电流及电容电压仿真波形。可以看出,随着占空比变化,电容电压波纹呈线性变化。即随着占空比的减小,电容电压波纹减小。这与式(15)相符。而电感电流波纹则如式(21)揭示的一致,即有多个极大值点和极小值点。仿真波形在3种情况下选取了2个极大值点和1个极小值点作为对比。

图9 2个模块d=0.875,0.5,0.25时电感电流及各电容电压波形Fig.9 Two module′inductive current and capacitor voltage waveform in d=0.875,0.5,0.25

图10 3个模块d=11/12,0.5,1/12时电感电流及各电容电压波形Fig.10 Three module′inductive current and capacitor voltage waveform in d=11/12,0.5,1/12
如图8~图10仿真结果是在各个极值点得到的,单个模块电感波纹幅值极大值为5.6 A,极小值约等于0A;两模块级联电感波纹幅值极大值为2.8 A,极小值约等于0 A;3模块级联电感波纹幅值极大值为1.8A,极小值约等于0A。不难发现,当级联模块数增加,电感波纹极大值随之减小。参照仿真结果可以发现,两模块级联后电感波纹极大值缩小到单个模块情况下的一半,而电感波纹等效频率增加1倍;而3模块级联后电感波纹缩小到单个模块的三分之一,电感波纹等效频率增加3倍。正符合式(21)及图7的分析结果。
5 实验验证
搭建了5.3 kW硬件实验电路装置,通过实验对理论分析进行了详细验证,实验中的各个参数选取如表2所示。

表2 三电平模块的实验参数Tab.2 Experimental parameters of three level module
2个模块级联实验中明显验证了级联后可以提高输入侧的电压等级。图11为输入电压在300 V时的4个输出电压波形和占空比为0.5时电感电流波形以及驱动信号。
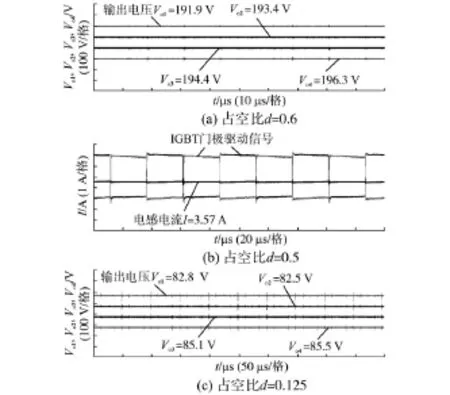
图11 两模块级联输出电压和电感电流实验波形图Fig.11 Two module′output capacitor voltage and inductive current experimental waveform
从实验波形可以看到三电平模块级联后仍然能够较好进行电压变换,输入电压为300 V,当占空比d=0.625时,经过两模块级联输出4个平行电压分别为191.9 V,193.4 V,194.4 V,196.3 V;当占空比d=0.5时电感电流波纹仍然几乎为0 A,输出电压分别为144.30 V,144.48 V,146.03 V,147.62 V;当占空比d=0.125时输出电压分别为82.8 V,82.5 V,85.1 V,85.5 V。2个模块级联基本保证了4个输出电压保持平衡且在占空比特殊点处电感电流波纹趋近零值。
在实验中同时验证了模块级联后电感波纹的倍频变化,图12为单模块和两模块级联同时在输入为300 V电压下的电感电流波形,可以很明显地看到两模块级联下的电感电流波纹几乎是单模块的2倍,而电感电流波纹峰值则恰恰相反。

图12电感电流波纹在单模块、两模块级联下的比较Fig.12 The comparison of inductive current ripple in single module and two modules cascade
图13为4个功率开关管所承受的电压应力,从图中可以很明显看出取值与4个输出电压基本保持一致,这与之前的理论分析也相吻合。说明模块级联后可以降低开关管所承受的电压应力。

图13 两模块级联开关电压应力Fig.13 The voltage stress in two module cascade
图14为两模块级联下的系统整体效率曲线图,其中横坐标为输出功率,纵坐标为变换器的效率值,系统的整体效率可以维持在98%以上。
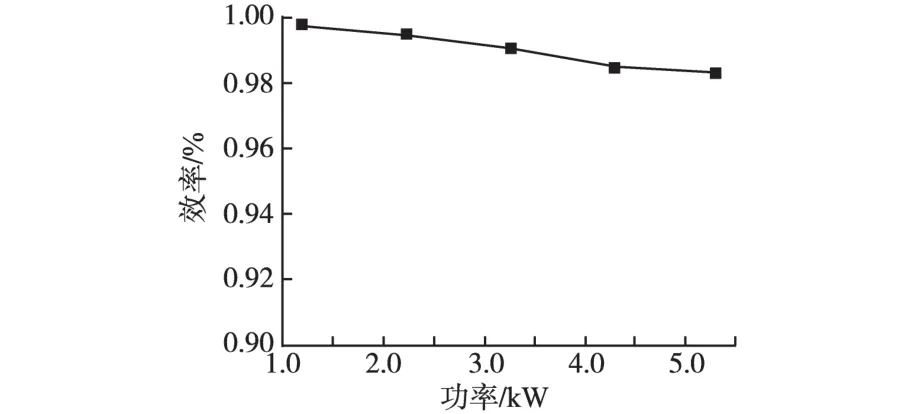
图14 系统效率曲线Fig.14 System efficiency curve
6 结论
针对高压级联多电平Boost直流变换器,以P-cell,N-cell构成的三电平模块为基础,详细分析了在载波移相调制下,变换器的变换过程,得到输出电压、输入电压、输出电流、输入电流等电气量的关系。并针对级联多电平结构对提升电感电流波纹等效频率进行了分析。通过仿真和实验,验证了高压级联多电平Boost直流变换器,能够极大增加电感电流波纹等效频率,减小电感波纹幅值。通过改变占空比,级联模块数能够在保证输出电压不变情况下,灵活接入不同等级电压。
[1]Huang A Q,Crow M L,Heydt G T.The Future Renewable Electric Delivery and Management(FREEDM)System:The Energy Internet[J].IEEE Proceedings,2011,99(1):133-148.
[2]Johann W Kolar,Gabriel Ortiz.Solid-state-transformers:Key Components of Future Traction and Smart Grid Systems[C]// Proceedings of the International Power Electronics Conference-ECCE Asia(IPEC),2014:877-882.
[3]陈元娣,林洁,刘涤尘,等.单一直流电源供电七电平级联逆变器的研究[J].电工技术学报,2012,27(2):45-51.
[4]Iman-Eini H,Farhangi S,Schanen J L,et al.Design of Power Electronic Transformer Based on Cascaded H-Bridge Multilevel Converter[C]//IEEE International Symposium on Industrial Electronics(ISIE).2007:877-882.
[5] 苏东奇,周雒维,罗全明,等.基于CDM升压单元的高增益Boost变换器[J].电力自动化设备,2014,30(7):15-20.
[6] 郦强,邓焰,何湘宁.单相APFC在变频器中的应用[J].电气传动,2005,35(11):22-24.
[7] 王梦琼,许春雨.单位功率因数与重复预测在APF中的应用[J].电气传动,2015,45(4):41-45.
[8]丘东元,张波,潘虹.级联型多电平变换器一般构成方式及原则研究[J].电工技术学报,2005,20(3):24-29,35.
[9]Khan F H,Tolbert L M,Peng F Z.Driving New Topologies of DC-DC Converters Fearturing Basic Switching Cell[J].Computers in Power Electronics,2006,17(6):328-332.
[10]Li S N,Tolbert L M,Wang F,et al.P-Cell and N-celll based IGBT Module:Layout Design,Parasitic Extraction,and Experimental Vefication[C]//Applied Power Electronics Conference and Exposition(APEC),2011.
[11]Imanini H,Farhangi S H,Schanen J L.A Modular AC/DC Rectifier Based on Cascaded H-bridge Rectifier[C]//Power Electronics and Motion Control Conference,2008.
[12]刘树林,刘健,杨银玲,等.Boost变换器的能量传输模式及输出纹波电压分析[J].中国电机工程学报,2006,26(5):120-124.
Research on High-voltage Cascade Multilevel Boost DC-DC Converter
LIU Chuang1,LI Hang1,SUN Zhoutong2,CAI Guowei1
(1.Electrical Engineering College,Northeast Dianli University,Jilin 132012,Jilin,China;2.Harbin Power Supply Bureau,Harbin 150001,Heilongjiang,China)
A new cascade multilevel boost converter topology was presented based on the basic three-level DC-DC converter in series for the higher voltage level,which can be used in the front-end converter of high-frequency isolation high-voltage DC converter and the intermediate power conversion of high-frequency isolation high-voltage PFC.The proposed multilevel boost converter is easily modulated with phase-shift control and can flexibly match different input-voltage level.The basic module can be described based on P-cell and N-cell concept offering the two equal output voltages and two times of the real-switching frequency.The operating principle of the proposed cascade boost converter was analyzed in detail with the phase-shift switching scheme including the performance of the inductor current and capacitor voltage ripples.And the relationship between the input and output voltage under the different duty ratio was discussed getting the variation tendency of the inductor current.Finally,a 5.3 kW experimental system was built to verify the proposed the performance characteristic of the cascade boost converter.
cascade multilevel boost converter;high-voltage DC converter;high-voltage PFC;inductor current ripple;capacitor voltage ripple
TM46
A
2015-04-10
修改稿日期:2015-12-22
国家自然科学基金(51307021);吉林省自然科学基金(20140101076JC)
刘闯(1985-),男,博士,硕士生导师,Email:victorliuchuang@126.com
