多跨海底管道横流向涡激振动预报模型
2016-10-12高喜峰谢武德徐万海
高喜峰,谢武德,徐万海
(天津大学 水利工程仿真与安全国家重点实验室,天津 300072)
多跨海底管道横流向涡激振动预报模型
高喜峰,谢武德,徐万海
(天津大学 水利工程仿真与安全国家重点实验室,天津 300072)
基于欧拉-伯努力梁理论确定了多跨管道结构振动方程,采用非线性Van der pol方程描述旋涡脱落的尾流动力特性,利用弹簧模拟两端和中间的复杂边界约束,构建了多跨海底管道横流向涡激振动预报模型。基于模态正交性展开流-固耦合作用方程,对各阶主坐标响应进行数值求解。对比了本模型预报结果与试验结果、软件分析以及DNV规范推荐值,吻合情况比较理想。本模型可为深海多跨管道涡激振动的研究、防范和治理提供有效的分析方法。
涡激振动;流-固耦合;尾流振子模型;多跨管道
Abstract:In this paper,the structure vibration equation of multi-span pipelines is deduced according to the Euler-Bernoulli beam theory.The dynamic behavior of wake flow is described by non-linear Van der pol equation.The complex constraint conditions in two ends and middle are modelled by springs.Based on the orthogonality of modes,the equation of the fluid-structure interaction is expanded,and the numerical solution of the main coordinate response of every mode is carried out.A model for predicting Vortex Induced Vibration (VIV) of multi-span pipelines is established.Comparing the results obtained by the present prediction model with the results from experiments,software and DNV recommended,it can be concluded that the present model performs very well.This model provides a valid method for the research,prevention and control of the VIV of the multi-span pipelines in deep sea.
Keywords:Vortex-Induced Vibration; fluid-structure interaction; wake oscillator model; multi-span pipelines
深海海底地势起伏不定容易导致海底油气输送管道出现悬跨现象。工程实践表明,涡激振动是造成悬跨管道出现结构疲劳损伤的重要原因。现阶段,针对单跨管道涡激振动问题的研究比较深入。余建星等[1]运用尾流振子模型研究了单跨管道涡激振动特性,并对比了模型实验结果与理论分析结果。李小超和王永学[2]基于频谱响应和升力曲线对海底单跨管道涡激振动进行了有限元求解。徐万海等[3]利用Van der pol尾流振子模型对海底悬跨管道的纯顺流向涡激振动进行了深入研究。Vedeld等[4]考虑了单跨管道的几何非线性,采用Rayleigh Ritz法对自由振动问题进行了研究。
随着海洋油气资源开采向着更深的海域进发,相关工程实践表明:深海海底管道常常出现多跨(两跨及两跨以上)。有关多跨管道涡激振动的探索起步较晚。Nielsen和Søreide[5]在试验水池中开展了多跨管道的模型试验,研究了在不同来流速度下多跨管道多模态涡激振动的响应情况;结果表明,增大来流速度,高阶模态可能被激发。Soni和Larsen[6]采用VIVANA和RIFLEX软件对涡激振动能量在相邻两跨管道之间的传递规律进行了研究。挪威科技大学的Koushan[7]在深入研究了海底悬跨管道涡激振动后,指出准确地分析预测自由悬跨段的涡激振动,必须考虑跨肩处的复杂边界、多跨间的相互作用等。
目前学术界和工程界缺乏分析多跨管道涡激振动有效的手段。基于上述不足,根据欧拉-伯努力梁理论和Van der pol尾流振子方程,考虑悬跨管道两端和中间的复杂约束条件,提出了多跨管道涡激振动预报模型。
1 数学模型
1.1结构模型
多跨海底管道可以两跨管道为基础进行扩展得到。本文取两跨管道为模型进行分析,建立如图1所示坐标系。其中l1和l2为悬跨长度,kr1、krm、kr2、kt1、ktm和kt2分别表示左端、中间和右端的扭转弹簧系数和拉伸弹簧系数;管外均匀来流速度为V,忽略管内流体速度,轴向拉力为T,管道直径为D,弯曲刚度为EI。

图1 两跨海底管道模型Fig.1 The model of two-span pipeline
根据欧拉-伯努利梁理论,管道在悬跨段l1和l2具有相同的结构振动方程:
式中:y为横向位移;x为轴向位移;t为时间参数;m=ms+min+ma为总质量,包括结构质量ms、管内流体质量min和管外附加质量ma(ma=CaπρD2/4,Ca为附加质量系数,通常取1.0,ρ为外界流体密度);c=cs+cl为总阻尼,包括结构阻尼cs=2mωnζ和水动力阻尼cl=CDρDV/2(ζ为无量纲结构阻尼比,ωn为结构固有圆频率,CD为拖曳力系数,其取值范围在1.2~2.0之间)。FL为旋涡脱落引起的涡激升力,计算公式为:
式中:CL为升力系数。
1.2尾流振子模型
当外界流体流经悬跨管道到达锁频区域,就会激发管道发生结构振动,管道结构振动又会改变外界流场特性,它们之间存在着强烈的耦合作用。Facchinetti等[9]总结了近30年来常见的尾流模型,发现加速度耦合振子模型最为理想。本文多跨管道尾流动力特性描述亦采用加速度耦合振子模型:
式中:q=2CL/CL0为无因次升力系数,CL0表示结构静止时的涡激升力系数,取值为0.3;ωs=2πStV/D为漩涡脱落频率,St为Strouhal数,取值为0.2;ε和A体现尾流振子和结构振动的耦合作用关系,可以结合相关实验数据对其进行标定。约化速度Vr=2πV/(ωnD)处于不同范围,参数A有不同的取值[10]:

结构最大响应幅值主要由约化质量阻尼参数SG(=8π2St2ζm/(ρD2))所决定。根据大量试验数据,确定模型参数ε,公式如下:
式中:γ=CD/(π2St)为迟滞因子。
2 模态及固有频率
多跨管道的模态对涡激振动响应幅值有重要影响,管道结构固有频率关系到响应频率和结构阻尼。在此利用边界约束条件对多跨管道的模态和固有频率进行求解。将管道的振动响应设为y(x,t)=φ(x)p(t),代入方程(1)中,忽略管道所受的外力和阻尼得到:
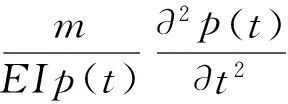

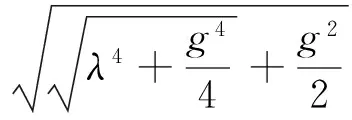
另外,时域微分方程:
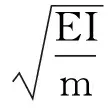
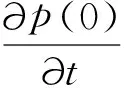
取φ1(x)和φ2(x)分别为悬跨段l1和l2的模态函数,cij(i=1,2;j=1,2…4)对应于模态函数中的各个系数,即:

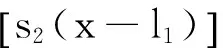
采用扭转弹簧和拉伸弹簧描述两跨管道两端和中间的复杂约束条件(如图1所示)。管道在悬跨段l1和l2的连接处应满足结构的位移y、转角θ、弯矩M和剪力N都连续,它们与模态函数的关系式有:
中间约束条件有:
悬跨段l1左端约束条件有:
同理,悬跨段l2右端约束条件有:
整理上述约束条件,可得关于cij的矩阵方程:
式中:H为8×8的方阵,系数列阵C=[c11c12c13c14c21c22c23c24]T。若方程(16)有非零解,则需满足|H|=0,得到关于λ的超越方程,采用割线法求解λ,再代回到式(16)中,解关于C的矩阵方程,利用最小二乘法求得C的最小模值。将得到的系数cij分别代入模态函数φ1(x)和φ2(x)中,最终可以获得悬跨段l1和l2的模态函数。由于λ可取多个值,故多跨管道有多个模态函数和固有频率。
3 流-固耦合振动方程
Srinil[11]在分析变张力立管受剪切流作用发生涡激振动时,采用模态分析的方法对立管结构振动和尾流振子模型进行简化。本文也采用此方法对多跨管道涡激振动流-固耦合振动方程进行展开。分别将结构运动响应式(17)和升力系数响应式(18)代入到式(1)和式(3)中,利用模态正交性可得到各阶主坐标pi(t)和di(t)的耦合作用方程组式(19)。
4 模型对比及分析
根据实际工况,多跨海底管道在外部来流的作用下一般很难激发高阶模态。本文选取前四阶模态进行理论分析,既能满足工程应用所需精度,又能节省计算资源。对流-固耦合振动方程采用Runge-Kutta法进行数值求解,通过傅里叶变换将时域响应转换成频域响应,得到涡激振动响应频率。
悬跨管道涡激振动的响应幅值和响应频率对管道的疲劳破坏有重要影响。在DNV规范DNV-RP-F105[8]中,对涡激振动的最大响应幅值给出详细的计算公式,在此做简要阐述,如下:
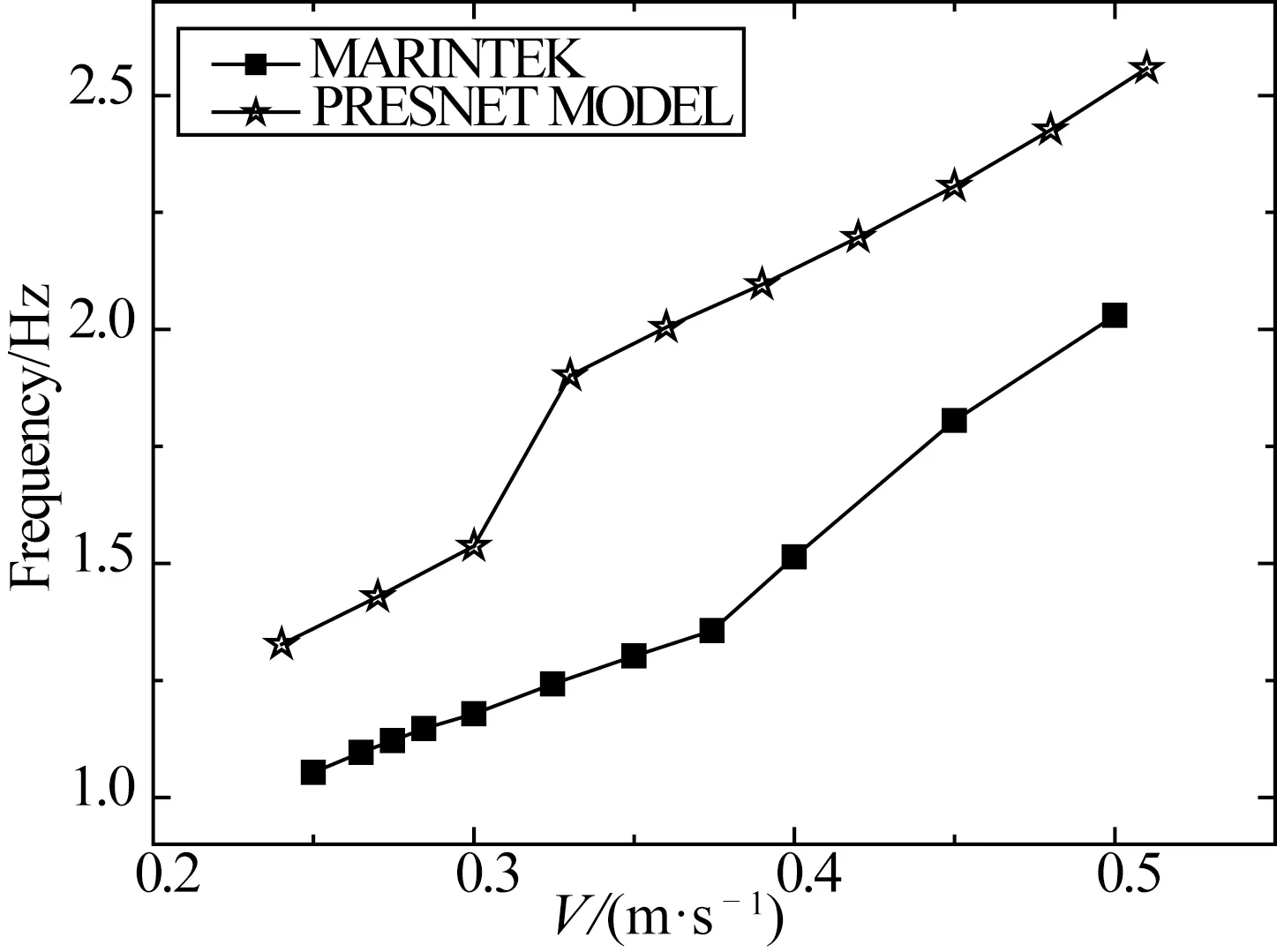
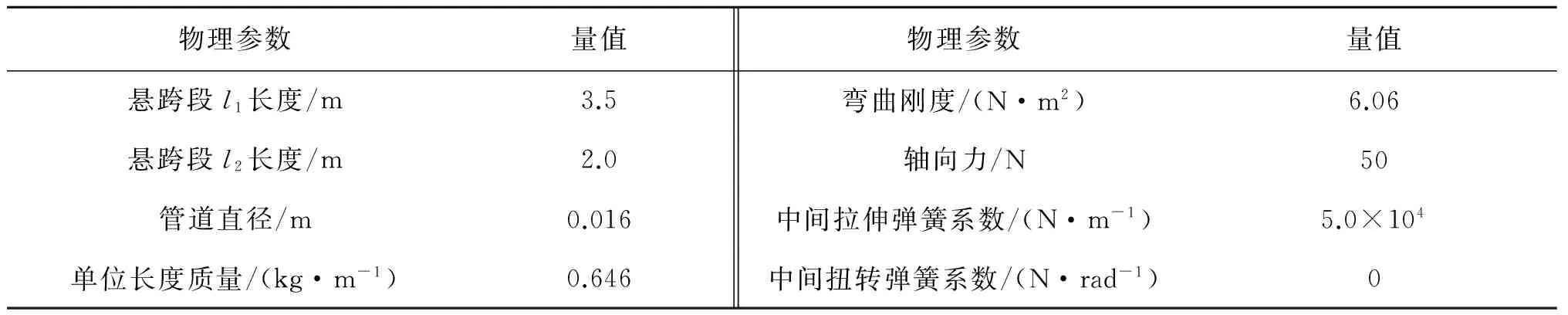
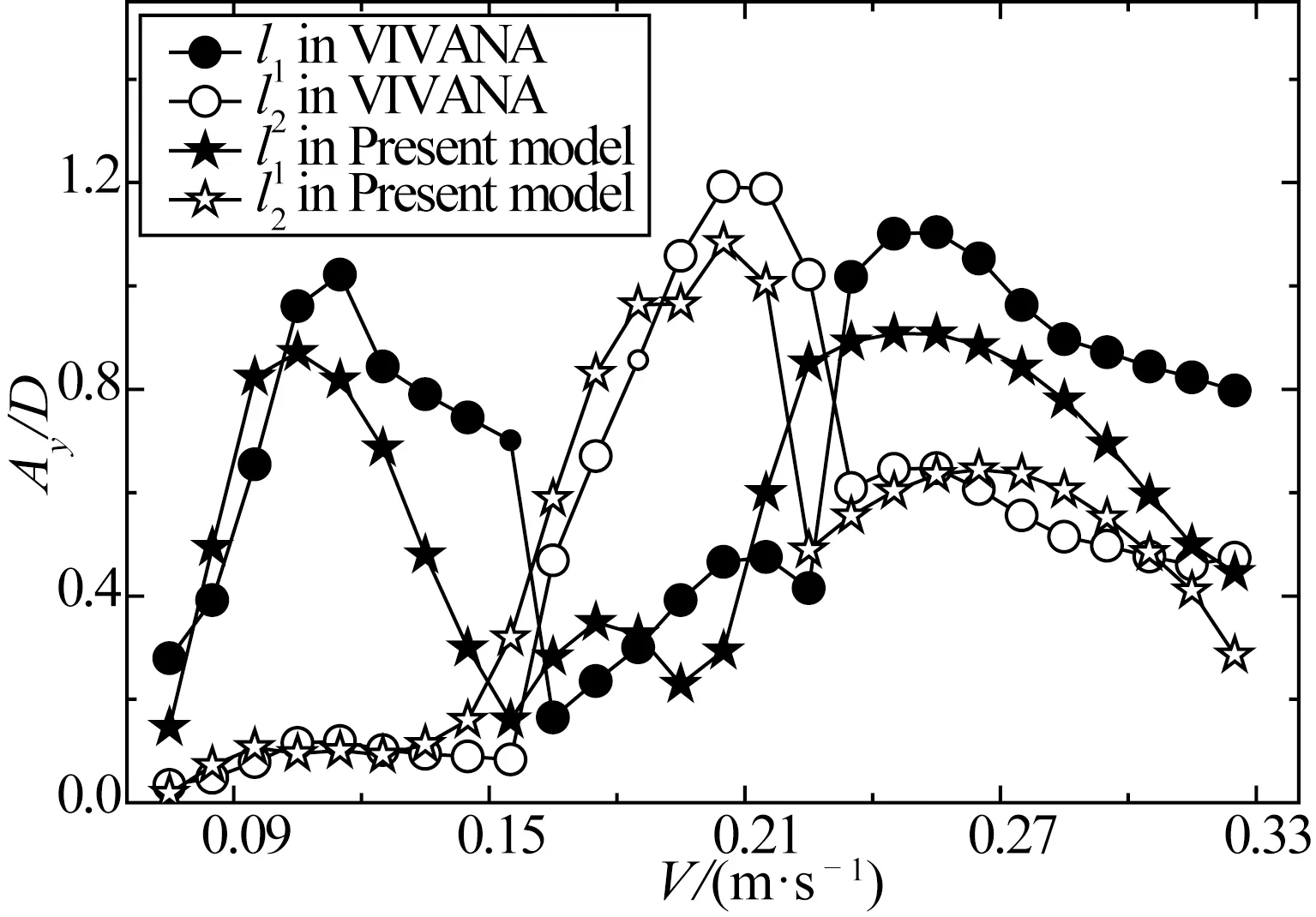
式中:η为相邻两阶固有频率的比值。基于经验模型的商用软件VIVANA也能够对简单多跨管道的涡激振动进行初步预估[6]。此外,Koushan[7]开展了一系列的模型试验,对多跨管道涡激振动进行了深入研究。为了验证本文所提出的多跨管道横流向涡激振动理论模型和数值计算的有效性,将本模型的计算结果与DNV-RP-F105规范推荐值、VIVANA软件计算结果和Koushan的试验结果进行对比分析。试验模型主要参数如表1所示,全局最大响应幅值和响应频率的对比结果分别如图2和图3所示。
从图2可知,增大外界来流速度,本模型计算得到的全局最大响应幅值偏小于DNV-RP-F105推荐值,偏大于试验结果,而与VIVANA软件的计算结果吻合较好。当来流速度V=0.94 m/s时,管道涡激振动开始由第一阶模态占主导;当1.40 m/s 图2 全局最大响应幅值Fig.2 The global max response amplitude 图3 响应频率Fig.3 The response frequency 表1 试验模型主要参数[7]Tab.1 The data of the model test 管道发生横流向涡激振动时,往往会伴随发生顺流向涡激振动。它们之间相互影响,存在着耦合作用。本模型忽略了顺流向的涡激振动,因而其在不同来流速度下的全局最大响应幅值(图2)和响应频率(图3)与试验结果存在数值上的差异。但其变化趋势与试验结果比较相似:随着外界流速不断增加,多跨管道的高阶模态将逐步被激发并对涡激振动响应幅值做出主要贡献,涡激振动的响应频率也逐渐增大。 Soni和Larsen[6]在对相邻两跨管道涡激振动之间的相互影响及能量传递规律进行分析时,基于频率响应利用VIVANA软件计算出悬跨段l1和l2的局部最大响应幅值。有鉴于此,本文也对局部最大响应幅值进行对比验证。主要计算参数如表2所示,对比结果如图4所示。 表2 VIVANA计算参数[6]Tab.2 The calculating parameters in VIVANA 图4 局部最大响应幅值Fig.4 The local max response amplitudes 从图4中可得知,随着外界来流速度的增加,两跨管道的涡激振动响应逐渐由高阶模态主导:当流速V在0.075~0.165 m/s之间时,悬跨段l1的最大响应幅值大于悬跨段l2的值,第一阶模态占主导;当0.165 m/s≤V<0.225 m/s时,局部最大响应幅值在悬跨段l1的值比在悬跨段l2的值要小,第二阶模态主导振动响应;当0.225 m/s≤V时,图中显示悬跨段l1的最大响应幅值反超悬跨段l2,第三阶模态成为控制模态。由本模型计算得到悬跨段l1和l2的局部最大响应幅值和模态主导区域都能够与VIVANA软件计算结果很好的吻合,进一步说明了本模型的有效性。 根据深海工程领域中常见的工程情况,对多跨海底管道横流向涡激振动进行了研究。基于两跨管道模型,根据欧拉-伯努力梁理论建立了管道的结构振动方程;采用Van der pol尾流振子方程描述尾流动力特性;运用扭转弹簧和拉伸弹簧对管道两端和中间进行约束,建立了均匀来流作用下多跨海底管道横流向涡激振动的理论预报模型。 本模型计算得到全局和局部最大响应幅值、响应频率和模态主导区域与DNV-RP-F105规范推荐值、试验结果以及VIVANA软件计算结果进行了对比分析,结果吻合较好,说明本模型具有一定的可行性。对于两跨以上的悬跨管道可以根据本模型的理论进行推导。本模型可为多跨海底管道涡激振动特性分析、疲劳评估、预防和治理提供一种有效的计算方法,在工程应用中具有较好的应用前景。 [1] 余建星,孙凡,傅明炀,等.海底管线涡激振动响应动力特性[J].天津大学学报,2009,42(1):1-5.(YU Jianxing,SUN Fan,FU Mingyang,et al.Dynamic characteristics of vortex-induced vibration of submarine pipeline[J].Journal of Tianjin University,2009,42(1):1-5.(in Chinese)) [2] 李小超,王永学.稳定流作用下海底悬跨管线涡激振动研究[J].船舶力学,2012,16(7):797-803.(LI Xiaochao,WANG Yongxue.Vortex-induced vibrations of free span pipelines exposed to steady currents[J].Journal of Ship Mechanics,2012,16(7):797-803.(in Chinese)) [3] 徐万海,余建星,刘健,等.海底悬跨输流管道纯顺流向涡激振动特性研究[J].船舶力学,2013 17(12):1481-1489.(XU Wanhai,YU Jianxing,LIU Jian,et al.Pure in-line vortex induced-vibrations of a free spanning pipeline conveying internal fluid [J].Journal of Ship Mechanics,2013,17(12):1481-1489.(in Chinese)) [4] VEDELD K,SOLLUND H,HELLESLAND J.Free vibrations of free spanning offshore pipelines [J].Engineering Structures,2013,56:68-82. [5] NIELSEN F G,SøREIDE T H.Dynamic response of pipeline in long free spans or multi-spans [J].Proc.of Euro-dyn,2005. [6] SONI P K,LARSEN C M.Dynamic interaction between spans in a multi span pipeline subjected to vortex induced vibrations[C]//ASME 2005 24th International Conference on Offshore Mechanics and Arctic Engineering.American Society of Mechanical Engineers,2005:255-263. [7] KOUSHAN K.Vortex induced vibrations of free span pipelines[D].Doctoral Dissertation,Norwegian University of Science and Technology (NTNU),2009. [8] VERITAS DN.DNV-RP-F105 Free spanning pipelines[S].February,2006. [9] FACCHINETTI M L,DE Langre E,BIOLLEY F.Coupling of structure and wake oscillators in vortex-induced vibrations[J].Journal of Fluids and Structures,2004,19(2):123-140. [10] XU W H,WU Y X,ZENG X H,et al.A new wake oscillator model for predicting vortex induced vibration of a circular cylinder[J].Journal of Hydrodynamics,Ser.B,2010,22(3):381-386. [11] SRINIL N.Analysis and prediction of vortex-induced vibrations of variable-tension vertical risers in linearly sheared currents[J].Applied Ocean Research,2011,33(1):41-53. Prediction model of multi-span pipelines subjected to Vortex Induced Vibration (VIV) in cross flow GAO Xifeng,XIE Wude,XU Wanhai (State Key Laboratory of Hydraulic Engineering Simulation and Safety,Tianjin University,Tianjin 300072,China) TV312 A 10.16483/j.issn.1005-9865.2016.02.006 1005-9865(2016)02-0041-06 2015-02-02 国家自然科学基金资助项目(51209161,51379144,51479135);国家自然科学基金创新研究群体科学基金资助项目(51321065);国家重点基础研究计划-973计划资助项目(2014CB046801) 高喜峰(1976-),男,辽宁人,副教授,硕士生导师,主要从事管土作用研究。E-mail:gaoxifeng@tju.edu.cn 徐万海。E-mail:xuwanhai@tju.edu.cn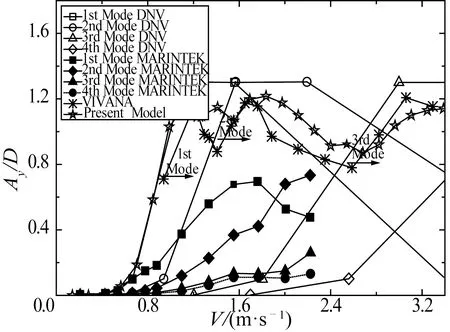

5 结 语
