圆形隧道围岩压力拱拱体范围的解析研究

吕燕，梁观山，陆莉娜，林水明，吴晓晨，李大鹏

（中国航空港建设第三工程总队，江苏南京211100）

·隧道与建设工程·

圆形隧道围岩压力拱拱体范围的解析研究

吕燕*，梁观山，陆莉娜，林水明，吴晓晨，李大鹏

（中国航空港建设第三工程总队，江苏南京211100）

为从理论上判定出压力拱拱体范围，以圆形隧道为例，分析了围岩二次应力状态，推导了水平应力及竖直应力公式，探讨了隧道上部岩体中水平、竖直应力变化趋势；在此基础上，结合3种不同的拱体判定方法，研究了各判定方法情况下的拱体范围，对比了各拱体判定方法之间的关系，可为工程实践提供参考。

圆形隧道；压力拱；拱体范围；解析

隧道开挖后，隧道周围岩体的应力状态会进行二次重分布，以达到优化自稳、最大限度发挥岩体自身承载能力，此即隧道围岩中的压力拱现象。1946年，Terzaghi通过“活动门实验”证实了砂土中存在拱效应，之后，国内外学者对压力拱现象进行了深入的研究［1-3］。压力拱研究的一个重要方面是确定拱体范围，目前，拱体范围的判定方法，见诸文献的主要有4种：一是贾海莉［4］等通过假设拱轴线方程（例如抛物线、列格氏悬线等），进而推导了压力拱的拱体范围；二是梁晓丹［5-7］等提出的拱体范围判定方法，他们认为，压力拱的外边界点可以根据最大主应力开挖前后的改变量大小来判定，压力拱的内边界点则为最大主应力的最大值处，在此方法的基础上，通过数值模拟分析了岩体参数对拱体范围的影响；三是喻波［8］等对梁晓丹等人的方法进行了改进，他提出“以最大主应力方向改变点作为压力拱外边界点、以最大主应力的极值点作为压力拱的内边界点”的拱体范围判定方法，通过数值模拟，系统研究了隧道跨度、岩体参数（主要是弹性模量E）对压力拱范围的影响，进而提出了隧道深埋与浅埋的划界方法；四是邹熹正［9］等提出的将场理论运用到压力拱的研究中，通过应力场的等值线、梯度线来确定压力拱的拱体范围，但这一理念提出之后并未出现新的研究成果。

由于压力拱赋存于岩体中，其本身即为岩体的一部分，以当前的技术手段尚不能通过试验直观地测量。目前，对于压力拱范围的研究，基于假设拱轴线方程的方法太主观武断而不符合实际情况，而依据计算机数值模拟的方法又不能很好地上升到一般理论规律的层面。鉴于此，本文在前人研究工作的基础上，以工程中常见的圆形隧道为例，对岩体中压力拱拱体范围进行了初步的理论探讨。

1　隧道围岩应力状态分析

1.1基本假设

假设圆形隧道围岩边界的竖向荷载为p0，水平荷载为λp0（图1），岩体各向同性，处于弹性应力应变阶段。

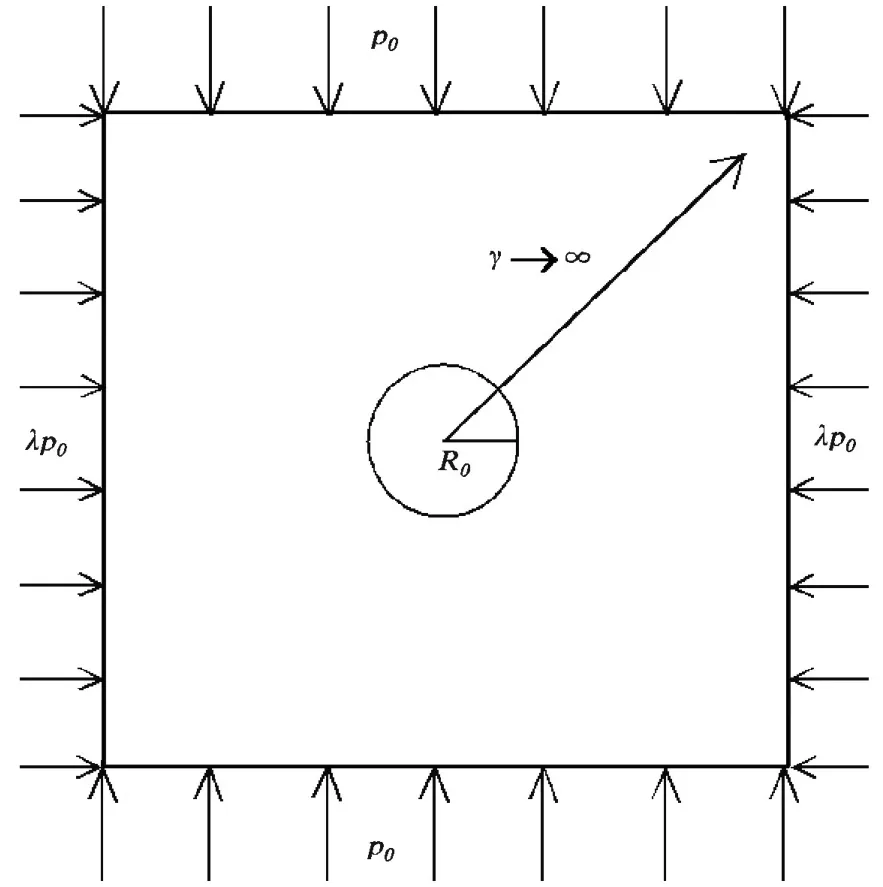
图1　隧道应力边界条件

本文只研究侧压系数0≤λ≤1的情况，对于λ＞1的情况，相当于图1中水平、竖直方向对换，因此不再赘述。

1.2隧道围岩的二次应力状态

根据弹性力学相关知识，可以求出隧道围岩的二次应力状态为：

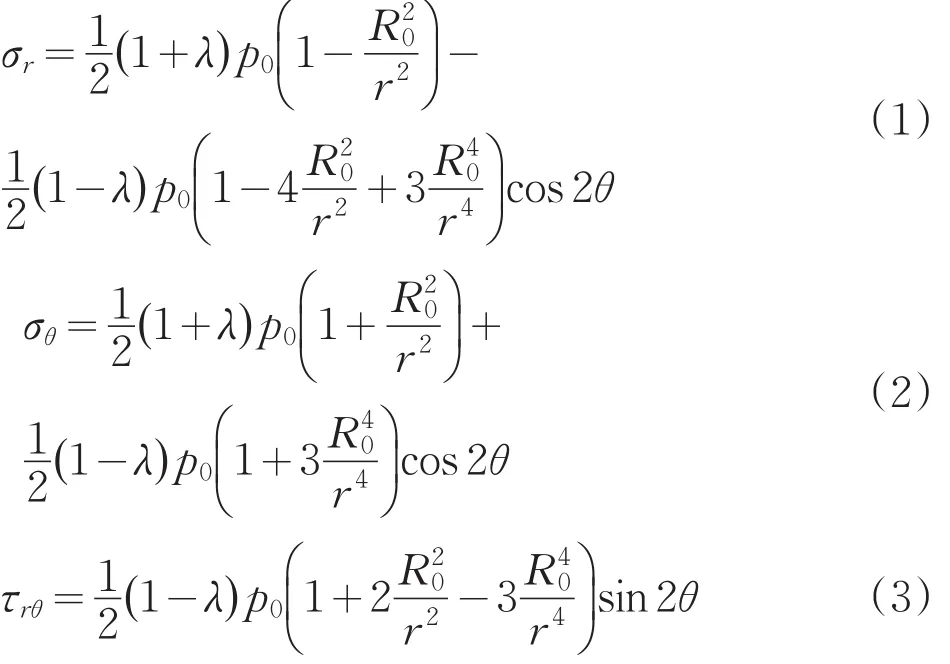
式中：σr——轴向正应力；

σθ——径向正应力；

τrθ——剪切应力；

θ——从水平方向起绕逆时针旋转的角度。

讨论：

（1）隧道壁应力状态分析：

当r=R0时，带入公式（1）、（2）、（3），得：

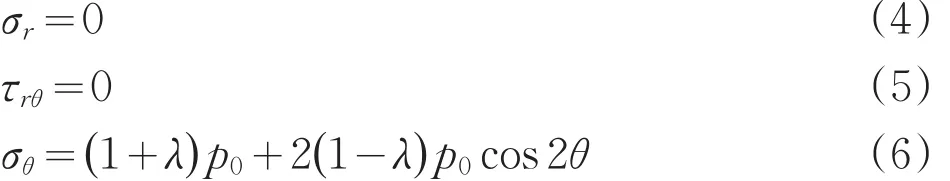
对于公式（6），侧压系数λ取不同值时，分别有：

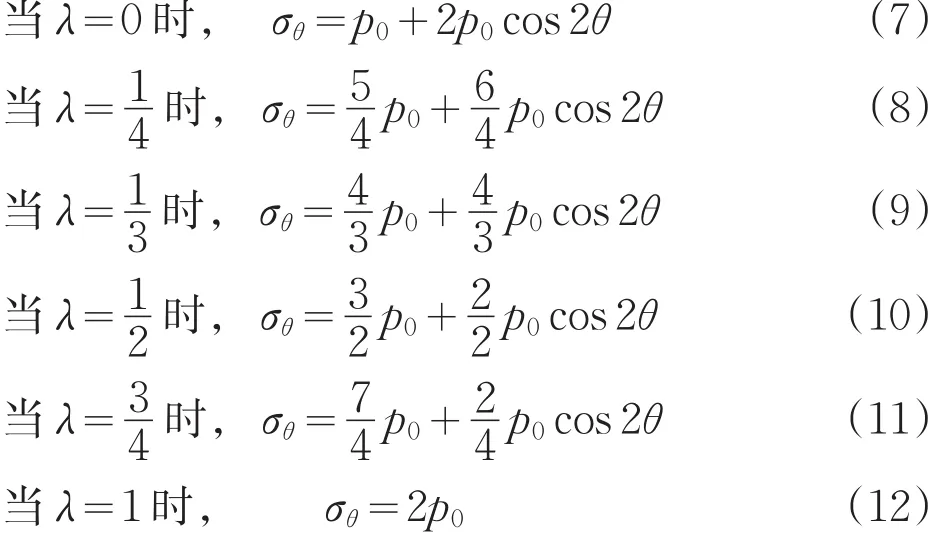
隧道壁上σθ值变化规律如图2所示。

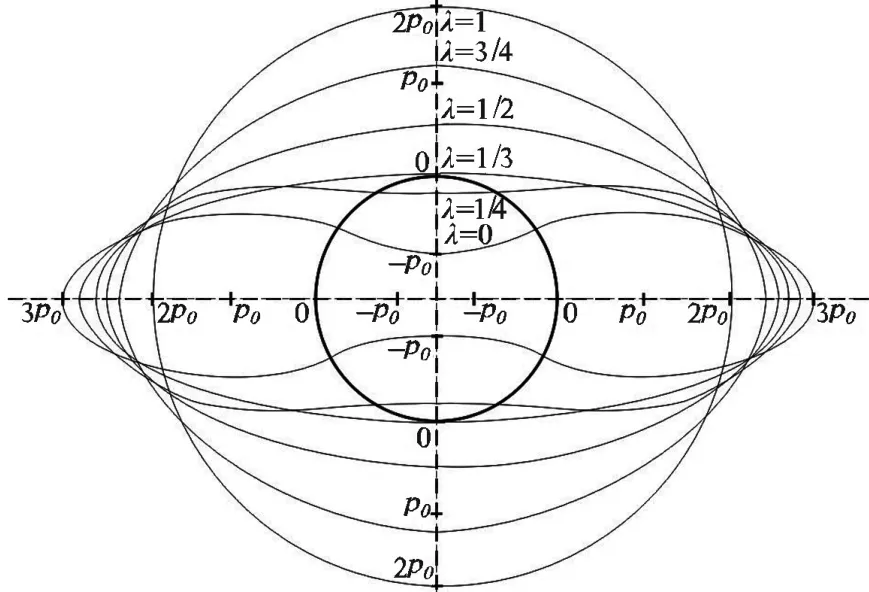
图2　隧道壁σθ变化规律

（2）隧道围岩水平、竖直应力状态分析：由σθ、σr、τrθ可以求出围岩中的水平应力σx和竖直应力σy。

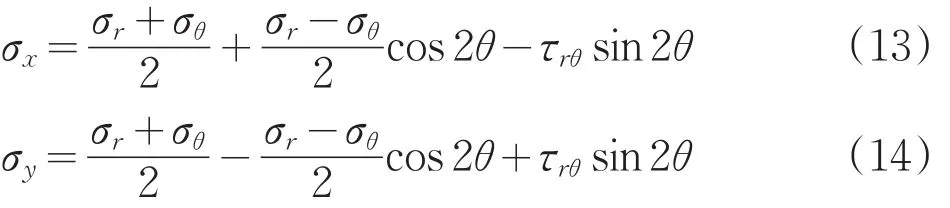
将公式（1）、（2）、（3）带入公式（13）、（14），可以求得：

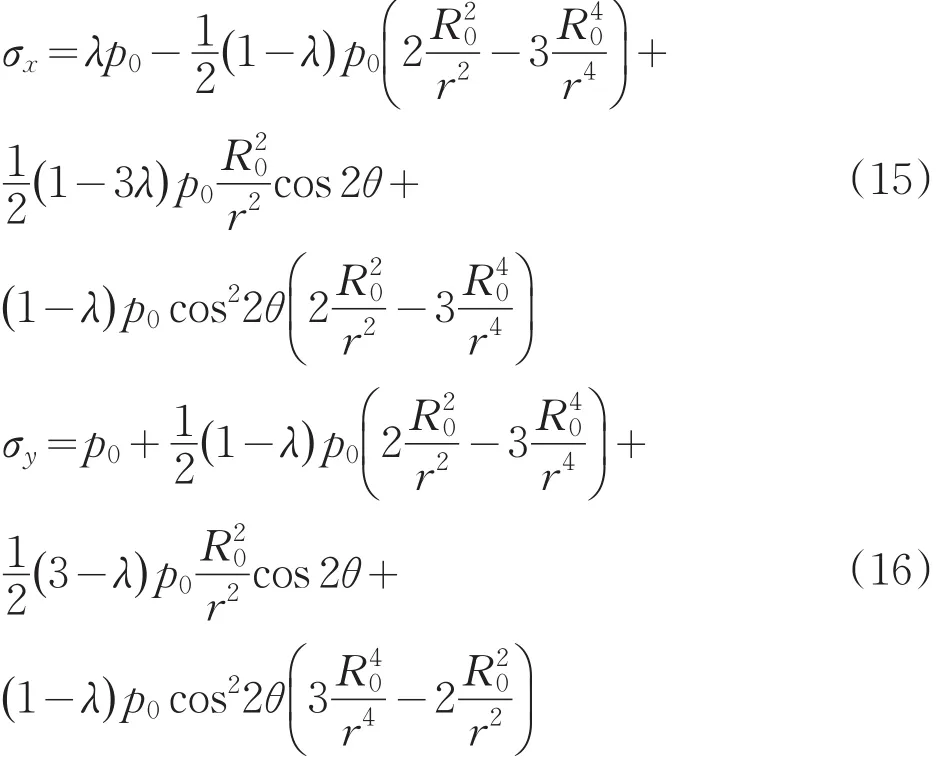
对于隧道顶部正中岩体，θ=90o，此时有：

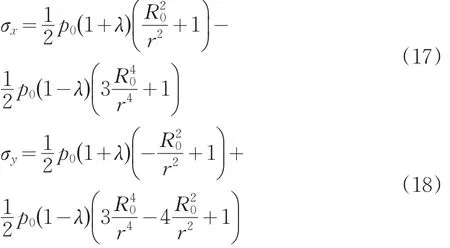
λ取不同值时，由公式（17）可得不同的σx，分析σx的大小变化趋势：

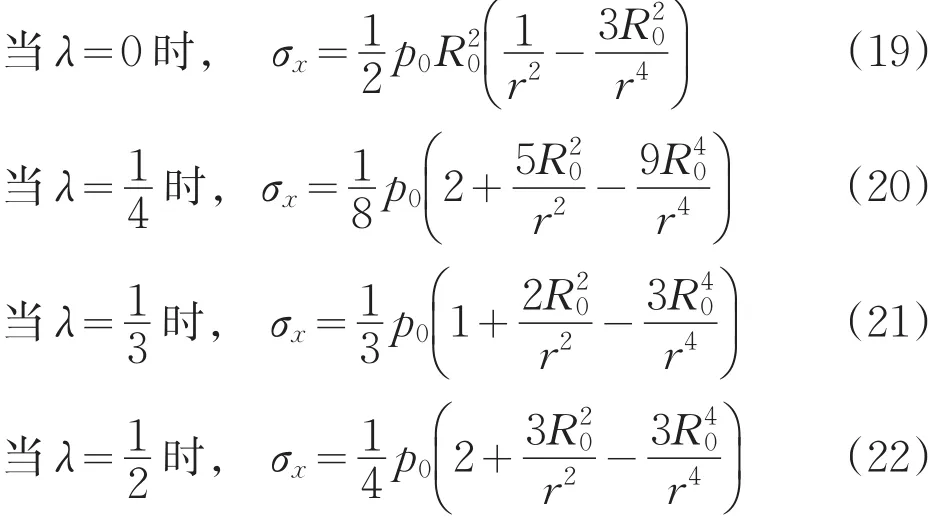
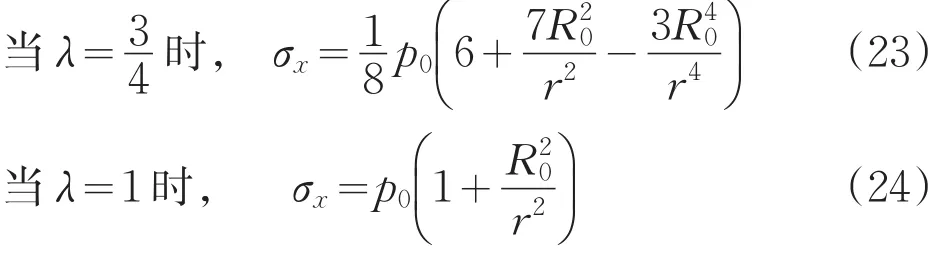
σx变化规律如图（3）所示［λ从0到1依次对应图（a）～（f）］：

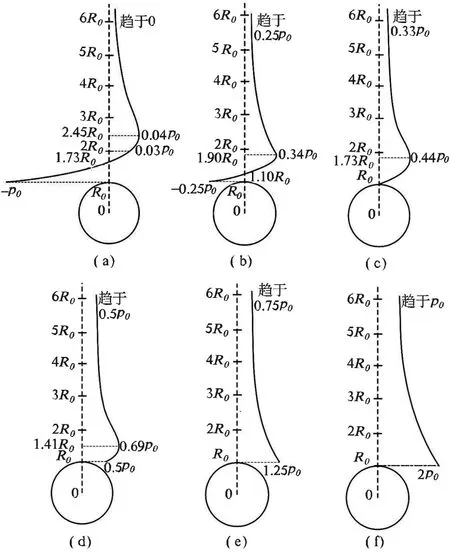
图3　隧道顶部围岩σx变化规律

λ取不同值时，由公式（18）可得不同的σy，分析σy的大小变化趋势：

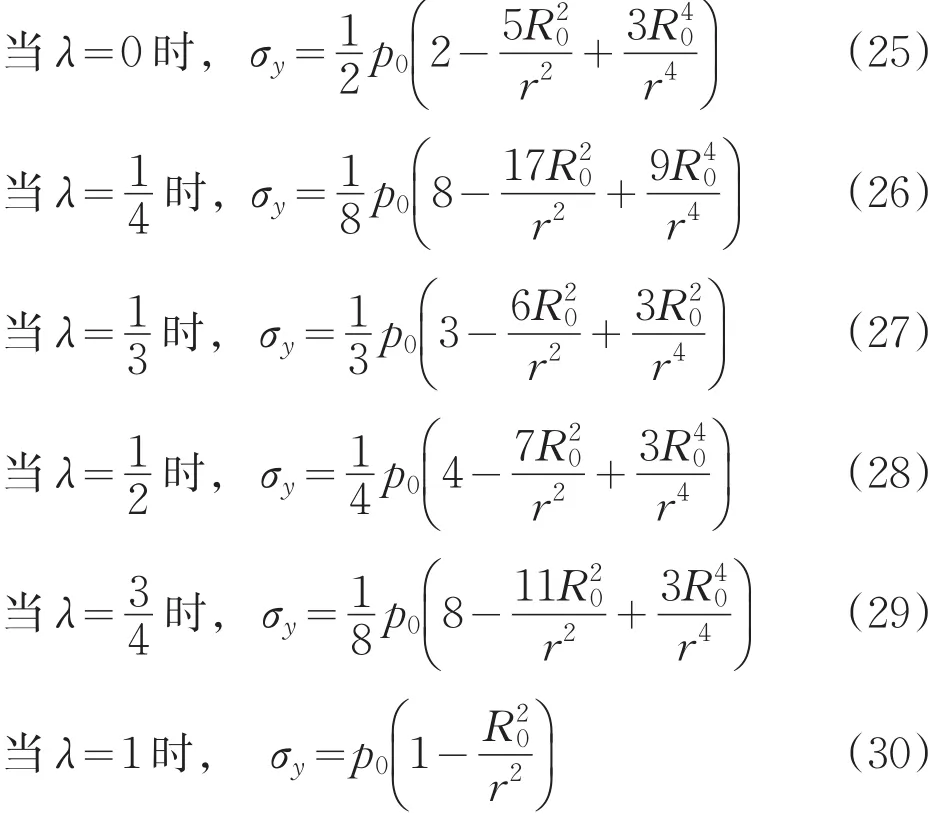
σy变化规律如图（4）所示［λ=0对应图（a）、λ=1/4对应图（b）、其余λ值对应图（c）］：

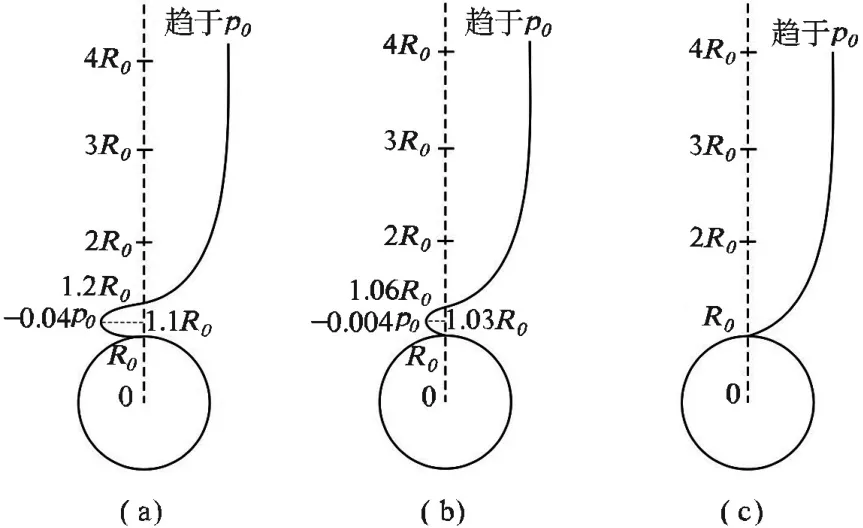
图4　隧道顶部围岩σy变化规律

2　拱体范围判定方法研究

2.1拱体范围判定方法一

拱体范围判定法法之一：隧道开挖前，岩体中的最大主应力为σy，隧道开挖后，由于应力重分布，出现压力拱现象，在隧道上部某点处，最大主应力由σy转变为σx，此点即为压力拱的外边界点（如图5所示，相较于外边界点，内边界点的位置不重要，文中不考虑）。

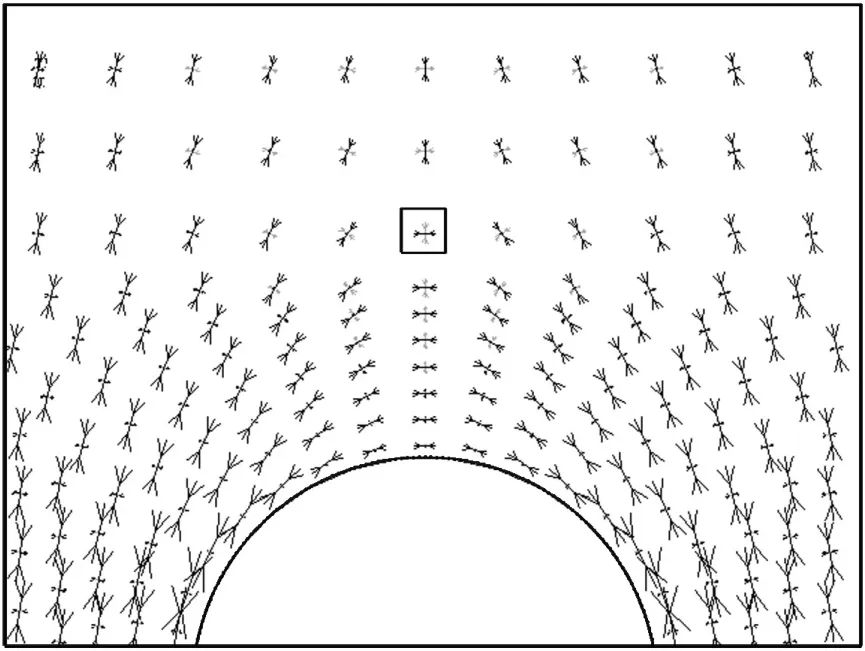
图5　最大主应力方向转变点

即：

将公式（15）、（16）带入式（31），化简可知：

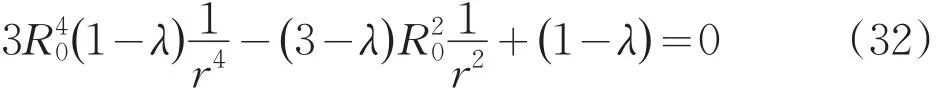
解得：

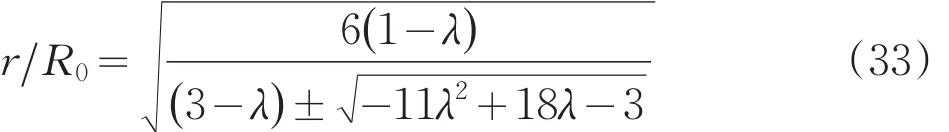
为使上式有意义，需有0.18＜λ＜1，当λ取不同的值时，拱体外边界点至隧道中心距离r与隧道半径R0的比值如表1所示。

由1.2节的应力状态分析可知，λ=0时，σx、σy之间不存在交点［图6（a）］，也即最大主应力方向一直保持σy方向，根据判定方法一，不存在压力拱外边界点，也即未形成拱效应。而λ=1/4时，σx、σy则有交点［图6（b）］，交点位于1.56R0处，此即为压力拱外边界点。

表1　拱体外边界点距离

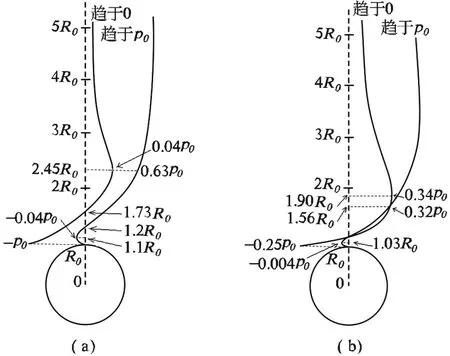
图6　隧道顶部围岩σx、σy关系

最大主应力方向由竖直转变为水平后，从直观上有形成“拱体”的感觉，这正是提出此判定方法的原因，但只有在隧道正上部才存在最大主应力由竖直σy转变为水平σx的现象，在其他位置的围岩中，隧道开挖后最大主应力转变的方向不确定，并不为水平的σx。因此，此方法只适合判定隧道正上部压力拱的拱体范围。

2.2拱体范围判定方法二

拱体范围判定方法二：隧道开挖后，由于二次应力重分布的压力拱效应，开挖后的σy值相比较开挖前会有所改变，根据σy改变量的大小来判定是否为拱体范围。

由公式（16）可知，对于隧道正中，θ=90°，r=R0时，σy=0。当r＞R0时，可以认为σy的值改变10%处为拱体范围边界，即：

化简，求解，可得：

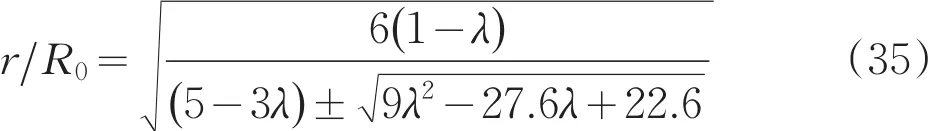
当λ取不同的值时，拱体外边界点至隧道中心距离r与隧道半径R0的比值如表2所示。

表2　拱体外边界点距离

由以上分析可知，采取变化量10%的方法可以判定出隧道上部拱体的范围，此方法亦可以判定其他部位围岩拱体的范围，另外，此方法中的改变量可以灵活选取，但取多大的改变量更科学则需具体分析论证。

由表2可以看出，围岩中3～5倍隧道半径距离就可以将扰动减小至小于10%左右。

2.3判定方法一与判定方法二的关系

现做进一步的分析，研究表1中的r R0数据对应多少σy改变量。λ=1 4时，r=1.56R0，反代入公式（16），得：

同理，分析可知：

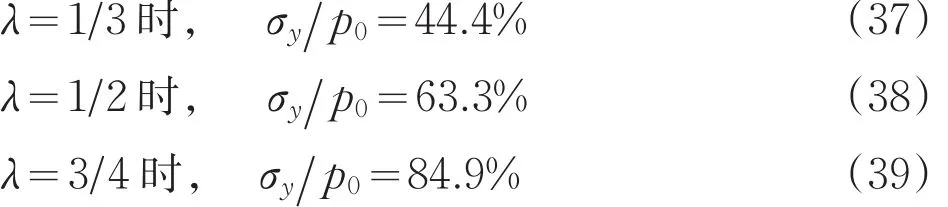
由此可见，以最大主应力方向转变点作为压力拱的外边界偏于保守，在最大主应力方向转变点之上很大一个范围内都存在明显的卸荷承载作用。

2.4拱体范围判定方法三

拱体范围判定方法三：以等值线判定压力拱拱体的范围，隧道开挖前，岩体中各处σy值都为p0，其等值线图是空白的；隧道开挖后，由于应力的二次重分布，隧道周边一定范围内的围岩σy值发生变化，可以其等值线图直观反映压力拱拱体范围。

例如，取λ=0、p0=1、R0=1的情况进行分析，由公式（16）可知：

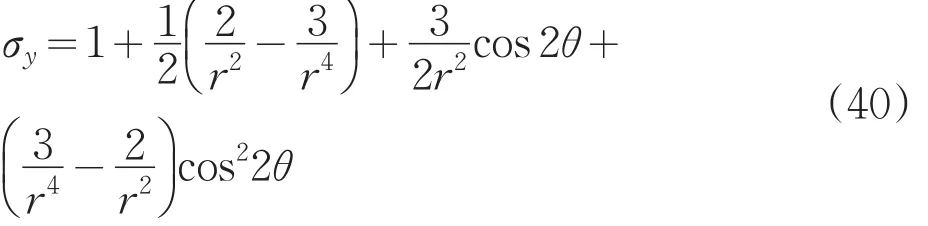
用matlab数学分析软件，可以绘制出隧道开挖后围岩中σy值的等值线图（图7）。由于R0取单位长度1，因此图7中的刻度尺数据代表的即为r/ R0值。由图7可以看出，对于值为0.9的等高线，也即隧道开挖前后σy变化值为10%时，其范围在隧道正上部扩展到r/R0=4.9处，与2.2节的理论分析一致。等值线图可以便利地反映隧道围岩不同位置处的应力变化情况，省却了大量繁琐的计算。由图7可以看出，在隧道上、下部，σy值比开挖前减小，相当于“拱”将竖向压力转变为拱体轴向压力向两侧传递；而在左、右两侧，σy值比开挖前增大，相当于“拱脚”。

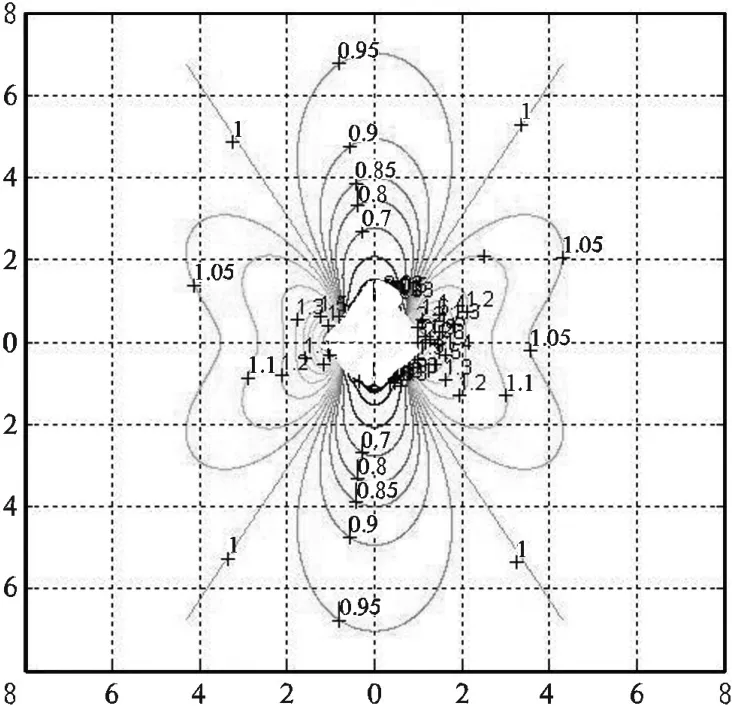
图7　隧道围岩σy的等值线图

等值线图具有直观形象的特点，有些时候需要用垂直于等值线的梯度线来表示压力拱的范围，在此不再赘述。

3　结论

本文推导了隧道围岩应力状态理论公式，在此基础上，结合不同拱体范围判定方法，确定出各判定方法情况下的拱体范围。可以看出，以“最大主应力方向转变点作为拱体外边界”的判定方法偏于保守，而以“应力值某改变量处作为拱体外边界”的判定方法则可以灵活应用，“等值线”判定方法借助隧道围岩应力等值线图，既直观形象又可以满足精度的要求。3种判定方法是从不同角度不同理念提出的，有其各自的合理性。

［1］王闯.大跨度地下岩石工程压力拱的研究［D］.中国矿业大学，2003.

［2］杜晓丽.采矿岩石压力拱演化规律及其应用的研究［D］.中国矿业大学，2011.

［3］关宝树.隧道力学理论［M］.成都：西南交通大学出版社，2008.

［4］贾海莉，王成华，李江洪.关于土拱效应的几个问题［J］.西南交通大学学报，2003，38（4）：398-402.

［5］梁晓丹，刘刚，赵坚.地下工程压力拱拱体的确定与成拱分析［J］.河海大学学报：自然科学版，2005，33（3）：314-317.

［6］梁晓丹，宋宏伟，赵坚.隧道压力拱与围岩变形关系［J］.西安科技大学学报，2008，28（4）：647-650.

［7］梁晓丹，赵坚，宋宏伟.围岩自调节成拱特性的实验与数值分析［J］.工程地质学报，2012，20（1）：96-102.

［8］喻波，王呼佳.压力拱理论及隧道埋深划分方法研究［M］.北京：中国铁道出版社，2008.

［9］邹熹正，乔福祥.对压力拱假说的新解释［J］.矿山压力，1989（11）：67-68.

TU432

A

1004-5716（2016）10-0165-05

2016-05-12

2016-05-25

吕燕（1978-），男（汉族），安徽东至人，工程师，现从事土木工程领域的科研和建设工作。