基于动态风浪环境的我国近海船舶避台航线优化
2016-10-12张进峰王晓鸥刘永森
张进峰, 王晓鸥, 刘永森
(1. 武汉理工大学 航运学院,武汉 430063;2. 国家水运安全工程技术研究中心,武汉 430063;3. 内河航运技术湖北省重点实验室,武汉 430063)
ZHANG Jinfeng1,2,3, WANG Xiaoou1,2, LIU Yongsen1,2
基于动态风浪环境的我国近海船舶避台航线优化
张进峰1,2,3, 王晓鸥1,2, 刘永森1,2
(1. 武汉理工大学 航运学院,武汉 430063;2. 国家水运安全工程技术研究中心,武汉 430063;3. 内河航运技术湖北省重点实验室,武汉 430063)
为提高船舶避台的安全性和经济性,提出基于动态规划算法的船舶避台航线优化模型。选取一个对我国近海船舶航行安全造成严重影响的台风天气过程作为研究对象,以我国近海一艘实际运营的散货船的典型航线为例,充分考虑船舶在大风浪中的风增阻和波浪增阻及其引起的失速特征,得出台风动态移动过程中的船舶避台航时最短航线。仿真结果表明:优化航线可安全、动态地避开台风的大风浪区。
气象导航;船舶避台;动态规划;动态风浪环境
ZHANGJinfeng1,2,3,WANGXiaoou1,2,LIUYongsen1,2
Abstract: In order to decide safe and economy route, the typhoon-avoiding optimization model is built based on dynamic programming algorithm. A typhoon, which harmed the offshore navigation safety severely, is picked as the typical condition, and a typical bulk carrier is chosen as the object ship. A typical voyage of the carrier is processed for optimization. The added wind resistance, the added wave resistance and the ship speed loss in the storm conditions are investigated. With the dynamic programming algorithm, the minimum-time route for avoiding typhoon is planed and automatically adjusted with the dynamic wind and wave environment. The simulation tests show that the optimized ship route can safely and dynamically avoid the typhoon storm area.
Keywords: weather routeing; typhoon avoidance; dynamic programming; dynamic wind and wave environment
台风是西北太平洋地区影响我国近海船舶安全航行的最严重的灾害性天气系统之一,而我国近海航行船舶通常很少采用气象导航,船长一般采用海上机动绕避等避台方法来减少台风灾害带来的损失。安全、科学、有效地避台是近海航行船舶实现安全生产和提高经济效益的基本保障。
近年来,相关学者围绕避台开展了诸多卓有成效的研究,确定台风的危险区域是保障船舶安全避台的关键。刘大刚等[1]在多源预报的基础上确定热带气旋危险区域;章文俊等[2]采用多级决策方法设计避台航线。此外,在船舶运动控制和台风信息的基础上设计高效、稳定的避台航线优化算法也是船舶实现安全、科学避台的关键。[3-5]通过对船舶绕避热带气旋的航行方案进行效益评价,可为航运公司开展避台工作提供参考,提高企业的经济效益。[6]通过对船舶和热带气旋未来的相对运动情况进行标绘,便于船舶驾驶人员制订绕避热带气旋的新航线。[7]
台风在发展过程中会因周围大型气压场分布的引导而移动,其产生的大风浪分布也随之动态变化,客观上增大了船舶避台的难度。在科学的台风路径和风浪预报的基础上,开展保障船舶安全的动态最优船舶避台航线研究是亟待解决的难题。
这里在保障船舶安全航行的基础上,以提高经济效益为宗旨,以保障船舶安全航行、选择动态风浪环境下航时最短的航线为优化目标,建立基于动态风浪环境的船舶避台航线优化模型。
1 船舶阻力增加值和失速计算
1.1船舶阻力增加值
船舶在大风浪中航行时,受波浪的扰动作用将产生纵摇、垂荡及横摇运动;同时,大风作用于船体及上层建筑上也将产生较大阻力,使得船舶航行阻力较静水中有所增加,船舶航速在主机功率不变的情况下较静水中有所下降。航行时风浪产生的阻力增加值是独立于船舶静水阻力的另一部分阻力。
根据船舶阻力与推进理论[8],船舶在大风浪中航行时的总阻力Rtotal具体可表示为
Rtotal=RT+δRwave+δRwind
(1)
式(1)中:RT为船舶静水阻力;δRwave为波浪导致的阻力增加值;δRwind为风导致的阻力增加值。
1.1.1船舶静水阻力
船舶静水阻力可表示为
RT=0.5CTρSV2
(2)
式(2)中:CT为阻力系数;ρ为海水密度;S为湿表面积;V为船舶静水航速。
1.1.2波浪导致的阻力增加值
不规则波可由一系列规则波叠加得到,因此不规则波导致的阻力增加值可由规则波中的波浪增阻和海浪谱得到。[8]
(3)
(4)
式(3)和式(4)中:R(ω)为规则波中的波浪增阻;ξ为波幅;ω为波频率;HS为有效波高;T为波周期;S(ω)为国际船级社协会推荐的皮尔逊-莫斯科维奇海浪谱[9]。
1.1.3风导致的阻力增加值
根据BLENDERMANN[10]通过风洞试验得出的风载荷模型,风作用于船体及上层建筑产生的附加阻力可表示为
(5)

(6)
式(5)和式(6)中:ρA为空气密度;Vw为海面风速;CDt和CDl分别为横风和迎风的风阻力系数;CDlAF为纵向拖曳系数;AF和AL分别为船舶水线以上船体的正面及侧面投影面积;ε为视风角(ε=0表示艏迎风);δ为交叉系数。风增阻相关系数取值见表1。
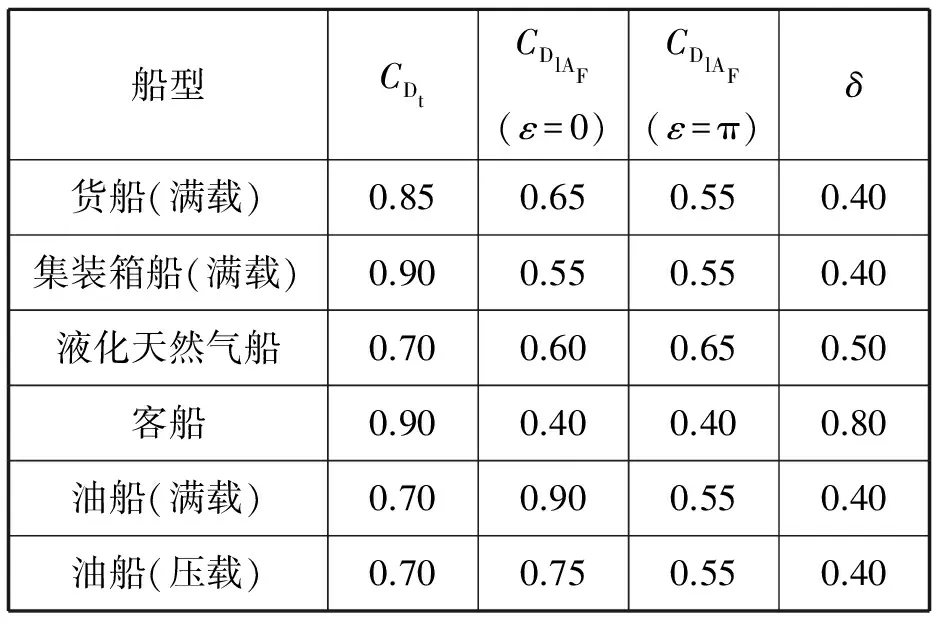
表1 风增阻相关系数取值
1.2船舶失速计算
船舶在静水中航行时的有效功率PE可表示为
PE=RTV
(7)
若假定船舶在风浪中航行时保持静水中的有效功率不变,则船舶有效功率[11]可表示为
PE=RTotal(Vr)Vr=RT(V)V
(8)
船舶以航速V航行时的有效功率可表示为
RTotal(V)V=RT(V)V+(δRwave+δRwind)V
(9)
式(8)和式(9)中:RTotal(Vr)为船舶以实际航速Vr在风浪中航行时的总阻力;RTotal(V)为船舶以航速V在风浪中航行时的总阻力;RT(V)为船舶以静水航速V在静水中航行时的总阻力。根据式(1)和式(2),将式(8)代入到式(9)中可得
RTotal(Vr)Vr=RTotal(V)V-(δRwave+δRwind)V
(10)

(11)
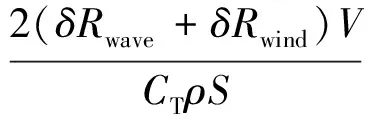
(12)
结合式(4),船舶实际航速Vr可表示为
Vr=f(HS,T,ω,CT,V)
(13)
2 动态规划算法
2.1基本思想
动态规划[12](Dynamic Programming)是一种解决多阶段决策过程问题的优化方法。所谓多阶段决策过程是指根据问题的特征将过程按时间、空间等标志分为若干个既相互联系又相互区别的阶段,在每个阶段都需做出决策,并在一个阶段的决策确定之后再转移到下一个阶段,从而使整体决策最优。
因此,各个阶段决策的选取不是任意的,既依赖于当前的状态,又影响以后的发展。当各个阶段的决策确定之后即组成一个决策序列,从而决定整个过程的一条航线。
2.2动态规划建模
优化目标是在最短的时间内避开台风。这里提出一种基于多阶段决策的建模方法,具体步骤如下。
2.2.1确定阶段变量
将避台优化航线的过程划分成n个阶段,即将船舶的出发点与目标点之间的海域按照海浪模式的计算网格划分为n个航行区段,阶段变量k=1, 2, …,n。
2.2.2选择状态变量
状态表示每个阶段开始时过程所处的自然状况。根据计算网格分布,船舶航行过程中每个阶段包含的状态有很多,该研究中每个阶段包含m个状态,状态数j=1, 2, …,m。描述状态的变量称为状态变量,主要有船舶的航速、位置等。状态变量主要描述过程的特征且无后效性,即当某阶段的状态变量给定时,该阶段之后过程的演变与之前各阶段的状态无关。在决策阶段k,状态变量可表示为

j=1,2,…,m]
(14)
2.2.3确定决策变量
当阶段k的状态确定之后可做出决策,从而演变到阶段k+1的某个状态,决定船舶下一阶段状态的变量是航向θ,决策变量θj(k)为k阶段的状态j处的船舶航向。
由决策组成的序列称为策略,从初始状态sj(1)开始的全过程的策略记作p1n(sj(1)),从第k阶段的状态sj(k)开始到终止状态的后部子过程的策略记作pkn(sj(k))。
2.2.4状态转移方程
在确定性过程中,一旦阶段k的状态和决策已知,阶段k+1的状态便完全确定。用状态转移方程表示这种演变规律为

(15)
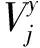
(16)
(17)
(18)
(19)
(20)
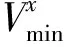
2.2.5指标函数和最优值函数
指标函数是衡量过程优劣的数量指标,是定义在全过程及所有后部子过程上的数量函数。阶段k的指标取决于sj(k)和θj(k),可表示为vk(sj(k))。在sj(k)给定时,指标函数vk(sj(k))对pkn的最优值称为最优值函数,记为fk(sj(k)),最优值函数可表示为
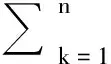
(21)
2.2.6递归方程
动态规划的递归方程是动态规划最优性原理的基础,递归方程可表示为
fk+1(sj(k+1))=min{vk(sj(k))+
fk(sj(k))},k=1,2,…,n
(22)
固定始端条件(航线出发点)的状态可表示为sj(1),自由终端条件(航线目标点)的最优值函数可表示为
fn(sj(n))=φsj(n)
(23)
式(23)中:φ为已知常量,表示船舶到达终点。
2.3问题求解

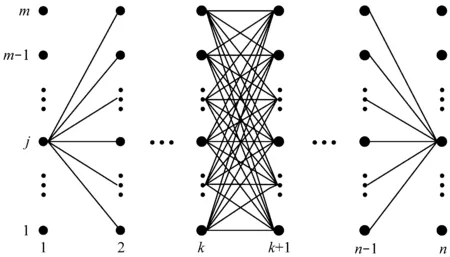
图1 动态规划递推格点
1)根据出发点对应时刻的风浪特征计算初始状态的船舶航速,令k=1。由于第1阶段是航线的初始阶段,因此船舶航行时间为0,即f1(sj(1))=0。
2)针对第2阶段所有出现的状态s1(2),s2(2),…,sm(2)计算各个状态的指标函数v2(s1(2)),v2(s2(2)),…,v2(sm(2)),进而确定最优值函数f2(sj(2))。
3)计算第k阶段各个状态的指标函数并确定k阶段的最优值函数,若式(23)成立,则转至步骤4),否则令k=k+1,转至步骤3)。
4)运用式(15)~式(20)和式(22),由k=n逆推至k=1求解最优路径。
由于气象和海洋预报的风场及波浪场数据的时间间隔一般为6 h,因此在运用动态规划算法实现避台航线优化的过程中,采用的风场和波浪场数据为6 h更新一次。
在船舶避台过程中,为保证船舶在大风浪中安全航行,在上述优化过程中提出以下2个限制条件:
1)将有效波高>5 m的区域设为禁航区域。
2)将海面风力>8级(风速Vw为17.2 m/s)的区域设为禁航区域。
具体表示为
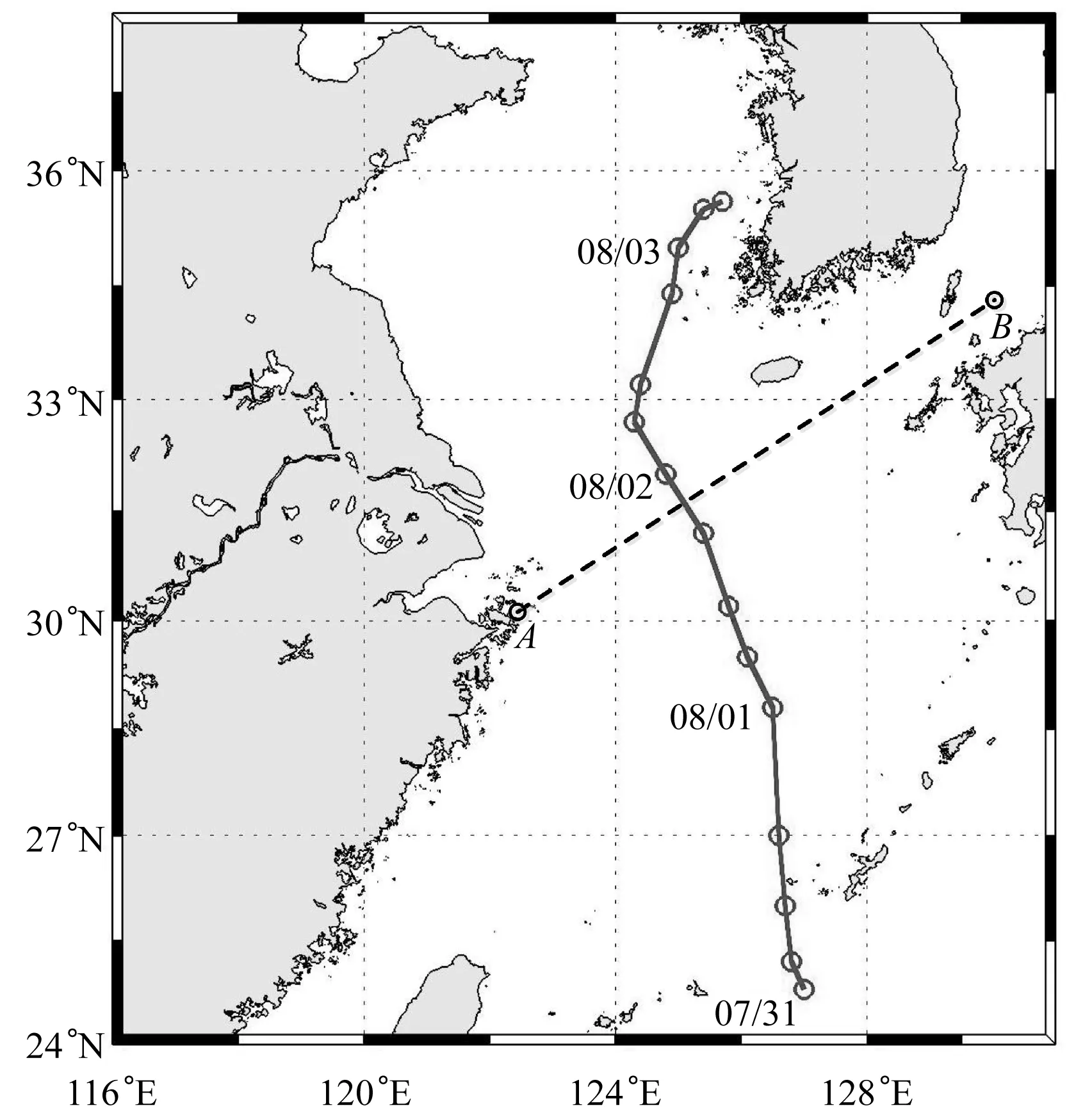
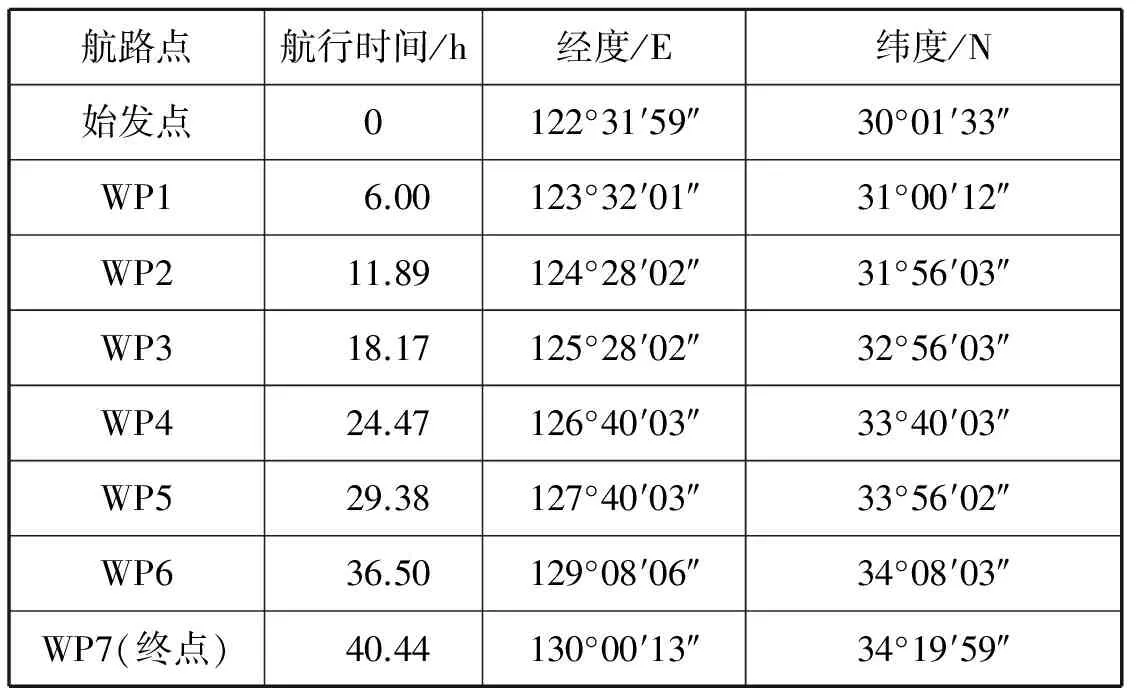
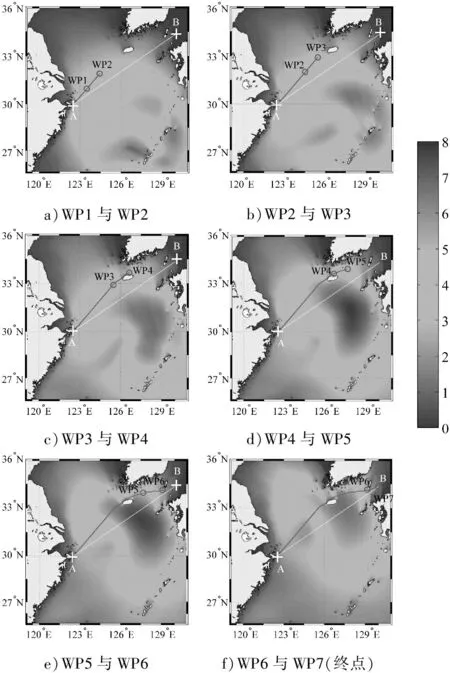
0 (24) 0 (25) 3.1台风实例及航线概况 据统计,每年影响我国的近海台风数约占西北太平洋地区台风总数的1/3,我国近海船舶航行安全受台风影响显著。这里以2014年第12号台风“娜基莉”(Nakri)为研究对象。该台风于2014年7月31日00时—8月3日00时(UTC)影响我国黄海、东海海域,其移动路径见图2(其中:实线为台风的移动路径;虚线为船舶计划航线)。 以我国近海航行的一艘实际运营的满载散货船为例,其船型主尺度为:垂线间长182.00 m;船宽32.26 m;型深15.80 m;设计吃水10.80 m;载重量45 000 t;设计航速14 kn。所选航线为我国舟山港至对马海峡的实际航线。图2中:航线起点A的位置为122°31′59″E,30°01′33″N,终点B的位置为130°00′13″E,34°19′59″N;船舶起航时间为2014年7月31日12时(UTC)。 图2 海浪模式计算区域 3.2海浪数值模拟 WAVEWATCH-Ⅲ海浪模式[13-14]模拟的计算区域为包括上述航线的黄东、东海海域,具体范围为116°E~131°E,24°N~38°N,海浪模式计算区域如图2所示。模式采用的水深数据为美国国家地理数据中心的全球1′×1′水下地形资料;模式采用的输入风场资料为美国国家环境预报中心每天6 h一次的再分析风场,该风场亦为风增阻计算的输入场。 海浪模式采用经纬度坐标的高分辨率等距水平正交网格,格距为4′×4′,每点的离散化波浪谱方向分辨率为15°,即24个方向,频率分辨率为0.041 8(即周期约为23.92 s)~0.41,以1.1 Hz因数间距,共25个频段;模式的初始化采用基于初始输入风场的风区受限的JONSWAP谱;采用的传播计算步长为600 s,地理空间传播步长和内部谱的传播步长也为600 s,源函数的积分时间步长为200 s。模拟时间为2014年7月31日00时—2014年8月3日00时,模式计算结果采用网格输出,每次时间间隔为3 h,模式输出参数为有效波高、平均波长、平均波周期及平均波向等。 3.3航线优化结果 根据以上海浪数值模拟、风增阻、波浪增阻和船舶失速计算,依据建立的船舶避台航线动态规划模型,得到优化后的船舶航路点(见表2),建立的船舶避台动态规划模型的航线优化结果为提出的安全限制条件下的航时最短航路,总航行时间为40.44 h。各航段的优化航路见图3,图3a~图3f分别为各航路点之间的优化航路分段,图中背景为对应各航段起点时刻的海面有效波高分布。船舶绕避台风一般采用加速、减速、绕航和滞航等方法,从台风移动方向的后侧通过。 表2 优化后的船舶航路点 图3 船舶优化航路和有效波高分布 由图3可知,由于“娜基莉”移动速度较慢,因此选择从台风移动方向前方航行通过求解优化航路。图中结果显示,优化航线较好地避开了台风的大风浪区,新航线可达到安全避离台风的目的。 针对我国近海船舶避台问题,利用动态规划算法建立船舶避台航线优化模型。利用WAVEWATCH-Ⅲ海浪模式对2014年第12号台风“娜基莉”的海浪场进行数值模拟。以我国近海的一艘实际运营散货船的典型航线为例,在充分考虑船舶在大风浪中受到风增阻和波浪增阻影响而造成船舶失速的基础上,得出特定安全限制条件和动态风浪环境下的航时最短避台优化航路。仿真结果表明,优化的航线能安全、动态地避离台风的大风浪区,证明该研究优化方法可行。该建模方法可为提高我国近海船舶避台航线的自动化程度提供理论依据。 [1] 刘大刚, 刘正江, 吴兆麟. 基于多源预报的热带气旋危险区域的确定方法[J]. 交通运输工程学报,2008,8(2):80-84. [2] 章文俊,魏淑义,李强,等. 使用多源预报确定船舶避台航线的多级决策方法[J]. 交通运输工程学报,2010,10(3):122-126. [3] 郭裕芳,马闯关,刘翔飞,等. 灾害性天气规避及航行方案选优系统[J]. 大连海事大学学报,2009,35(4):21-25. [4] 汤青慧,陈戈,刘艳艳. 一种智能化的避台航线设计方法[J]. 中国海洋大学学报,2011,41(6):104-108. [5] 高宗江,张英俊,朱飞祥,等. 远洋船舶避台航线设计算法[J]. 大连海事大学学报,2013,39(1):39-42. [6] 吴金龙,马轲馨,范中洲,等. 船舶绕避热带气旋方案效益评估[J]. 大连海事大学学报,2010,36(2):31-34. [7] 吴金龙,白春江,刘大刚,等. 船舶-热带气旋动态标绘系统[J]. 中国航海,2013,36(2):114-119. [8] BERTRAM V. Practical Ship Hydrodynamics[M]. 2nd ed. Oxford: Elsevier Ltd, 2012:74-93. [9] IACS. Standard Wave Data[R]. London: International Association of Classification Societies, 2001. [10] BLENDERMANN W. Parameter Identification of Wind Loads on Ships[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1994, 51:339-351. [11] LIN Y, FANG M, YEUNG R. The Optimization of Ship Weather-Routeing Algorithm Based on the Composite Influence of Multi-Dynamic Elements [J]. Applied Ocean Research, 2013, 43:184-194. [12] 吴沧浦. 最优控制的理论与方法[M]. 北京:国防工业出版社,2013:94-98. [13] TOLMAN H L. User Manual and System Documentation of WAVEWATCH III Version 3.14 [R]. NOAA/NWS/NCEP/MMAB, Technical Note 276, 2009. [14] 黄立文,张进峰. 影响近海船舶航行安全的台风浪数值预报试验[J]. 中国航海,2005,28(2): 52-56. DynamicOptimizationofShipTyphoonAvoidanceRouteinginChinaOffshoreWaters (1. School of Navigation, Wuhan University of Technology, Wuhan 430063, China; 2. National Engineering Research Center for Water Transport Safety, Wuhan 430063, China; 3. Hubei Inland Shipping Technology Key Laboratory, Wuhan 430063, China) U692.31;U698.91 A 2016-01-10 国家自然科学基金(51209166);国家留学基金(20133018);武汉理工大学自主创新研究基金(2014-Ⅳ-095) 张进峰(1980—),男,安徽无为人,副教授,博士,从事水上交通安全与环境研究。E-mail:mount@whut.edu.cn 1000-4653(2016)02-0045-053 航线优化实例
4 结束语
