敏捷卫星对目标访问信息的计算方法
2016-10-11刘晓东郭建恩何川东邹冬冬
刘晓东,王 鹏,林 元,郭建恩,何川东,崔 莉,邹冬冬
(北京市遥感信息研究所,北京 100192)
敏捷卫星对目标访问信息的计算方法
刘晓东,王鹏,林元,郭建恩,何川东,崔莉,邹冬冬
(北京市遥感信息研究所,北京 100192)
任务分解是任务规划的前提,其核心是计算卫星对目标的访问信息,即计算卫星访问目标时的姿态角、实际地面分辨率和太阳高度角。首先计算目标点在地心空间直角坐标系中的坐标,经过多次坐标转换,得到目标点在卫星轨道坐标系中的坐标,从而可以计算出相应时刻卫星对该目标的二维指向角度。在此基础上,根据卫星成像原理,分别计算光学卫星和雷达卫星的实际地面分辨率。最后,通过计算太阳赤纬和太阳时角,得到太阳高度角。
敏捷卫星;对地观测;访问信息;计算
0 引言
传统的非敏捷卫星只具有一维姿态指向自由度[1-2],只能进行滚动成像或俯仰成像[3-4],敏捷型卫星依靠姿态控制系统控制卫星整体灵活摆动[5],卫星可以在一个较长的可见时间窗口内,自由选择其中一个时段从不同角度对目标进行观测[6],成像灵活性远大于传统卫星[7]。因此,敏捷卫星任务规划问题复杂度远大于传统卫星[8-10],不同的观测时刻对应不同的观测角度产生了多种可能的观测方案[11-15],较长的可见时间窗口等因素都增大了解空间[16-18],求解敏捷卫星任务规划问题的首要条件就是建立卫星和目标相对运动模型,研究任意时刻卫星对目标观测姿态角度的计算方法[19-20]。
在卫星和目标相对运动模型建立过程中,假设卫星的姿态机动有滚动和俯仰构成,按照先滚动后俯仰的顺序完成姿态机动,且忽略卫星质心与星载传感器间的距离。计算敏捷型卫星二维指向实际上是计算卫星传感器指向目标方向矢量在卫星本体坐标系中的精确位置,在计算过程中涉及多个坐标系之间的坐标转换[21-23]。
1 卫星与目标相对运动模型
(1) 计算目标点在地心空间直角坐标系(地固系)中的坐标
目标T地理经纬度(测地经纬度)为(long,lat),T在地心空间直角坐标系中坐标(忽略高度)为:
(1)
(2)目标点在地固系中的坐标转换为瞬时真赤道地心系中的坐标
首先忽略地球极移的影响,将目标T在地固系中的直角坐标近似为准地固系中的直角坐标,然后将准地固系中的直角坐标转换到瞬时真赤道地心系:
(2)

(3)目标点在瞬时真赤道地心系中的坐标转换为瞬时平赤道地心系中的坐标
考虑章动的影响,目标点在瞬时平赤道地心系中的坐标为:
V2(T)=Rz(Δμ)Ry(-Δθ)Rx(Δε)V1(T),
(3)
式中,Δμ=Δφcosε为赤经章动,Δθ=Δφsinε为赤纬章动,Δε为交角章动,Δφ为黄经章动。
(4)目标点在瞬时平赤道地心系中的坐标转换为历元平赤道地心系(J2000惯性系)中的坐标
考虑章动的影响,目标点在历元平赤道地心系(J2000惯性系)中的坐标为:
V3(T)=Rz(ζA)Ry(-θA)Rz(zA)V2(T),
(4)
式中,ζA、zA、θA为3个赤道岁差参数。
(5)目标点在历元平赤道地心系(J2000惯性系)中的坐标转换为地心轨道坐标系中坐标
目标点在地心轨道坐标系中的坐标为:
V4(T)=RZ(ω+f)RX(i)RZ(Ω)V3(T),
(5)
式中,Ω为历元时刻t对应的卫星升交点赤经;i为历元时刻t对应的卫星轨道倾角;ω为历元时刻t对应的卫星近地点幅角;f为历元时刻t对应的卫星真近点角。
(6)目标点在地心轨道坐标系中坐标转换为卫星轨道坐标系中坐标
目标点在地心轨道坐标系经坐标系旋转+沿z轴平移转换为卫星轨道坐标系:
(6)
式中,RES为历元时刻t对应的卫星质心到地心距离。
2 二维指向角度计算
在卫星轨道参数确定的情况下,经过上述坐标转换,可得到任意时刻目标T在卫星轨道坐标系下的位置坐标,由目标在卫星轨道坐标系下的位置坐标可以计算出相应时刻卫星对该目标的观测摆角。卫星经过姿态机动,将相机光轴指向目标;姿态角为卫星本体坐标系相对于卫星轨道坐标系的转动角度,数值与转动顺序相关,本文假设卫星的转动顺序为先滚动后俯仰,示意图如图1所示。

图1 滚动、俯仰二维指向示意图
卫星传感器指向矢量在卫星本体坐标系中为(0,0,1),即指向卫星本体坐标系z轴;不进行姿态机动时,卫星本体坐标系与卫星轨道坐标系重合;先绕x轴转动滚动角θR,再绕y轴转动俯仰角θP后,相机光轴矢量(本体坐标系z轴方向)指向目标。
由图1可见,俯仰角θP、滚动角θR为:
(7)
根据t时刻目标在卫星轨道坐标系下的位置坐标(xt,yt,zt),由式就可以确定θP和θR,对于非敏捷卫星,俯仰角θP=0,可以得到x=0,位置坐标中x最接近0的时刻即为卫星对目标的访问时刻。根据该时刻的y和z坐标,可以确定滚动角θR,即卫星访问目标的侧摆角。对于敏捷卫星,由于俯仰角θP并不为0,因此,卫星对目标的访问窗口并不是单一时刻,而是一个时间段,该时间段的范围与俯仰角和滚动角的取值范围有关。
3 实际地面分辨率计算
3.1针对光学卫星
当卫星进行星下点成像时,星载遥感器的地面像元分辨率GSD0与像元尺寸d、相机焦距f以及轨道高度H的关系为:
(8)
当卫星进行侧视成像时,成像距离随侧摆角的增加而增大,因而会引起星载遥感器的地面像元分辨率的下降。当侧摆角为α时,将地球近似看作圆球体,地球半径为R,像元在地面上的成像区域如图2所示。
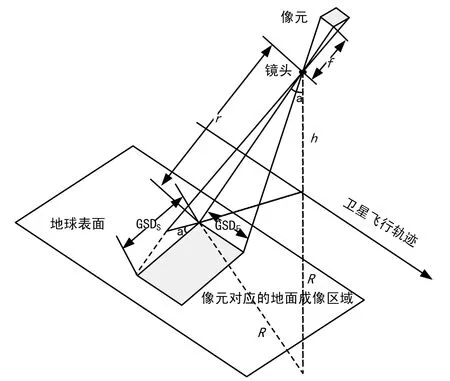
图2 像元与其地面成像区域的几何关系
从图2中可以看出,卫星与成像区域的距离r为:
(9)
卫星飞行方向的地面像元分辨率GSDF为:
(10)
星载遥感器扫描方向的地面像元分辨率GSDS为:
(11)
3.2针对雷达卫星
由于星载SAR的侧向成像特点,雷达图像的分辨率要分为距离向和方位向两个部分,而且二者是互不相关的。距离向分辨率是脉冲在其发射方向上(距离向)能分辨两个目标的最小距离,方位向分辨率是在辐射波垂直的方向上(方位向)相邻的两束脉冲之间能分辨的两个目标的最小距离。
星载SAR的方位向分辨率ρd只与雷达天线的真实孔径长度D有关,而距离向分辨率ρg与光速c、脉冲带宽B以及入射角θ有关,ρd和ρg的计算公式分别为:
(12)
(13)
4 太阳高度角计算
太阳高度角指太阳光线和地面目标所在地平面的夹角,当太阳垂直照射地面目标时光线条件最好,此时太阳高度角为90°。太阳高度角随着地方时和太阳的赤纬的变化而变化。
已知点目标的经纬度坐标为(λ,φ),所在时区为ζ,卫星观测该目标的中心时刻为t,对应的年、月、日、时、分、秒分别为ty、tmo、td、th、tmi、ts。太阳高度角Hs与太阳赤纬δ、太阳时角ψ的关系为:
sinHs=sinφsinδ+cosφcosδcosψ。
(14)
太阳赤纬又称赤纬角,是地球赤道平面与日地中心连线之间的夹角,由于地球自转轴与公转平面之间的角度基本不变,因此太阳的赤纬随季节不同而有周期性变化,变化的周期等于地球的公转周期。太阳赤纬与日角σ有关,即:
δ=0.372 3+23.256 7sinσ+0.114 9sin2σ-0.171 2sin3σ-
0.758cosσ+0.365 6cos2σ+0.020 1cos3σ;
(15)
日角与积日N的关系为:
σ=2π(N-N0)/365.242 2,
(16)
式中,N0与观测时刻的年份有关,即:
N0=79.676 4+0.242 2(ty-1 985)-「(ty-1 985)/4⎤。
(17)
积日是日期在年内的顺序号,例如,1月1日的积日为1,平年12月31日的积日为365,闰年则为366。积日与观测时刻以及目标所在时区的关系为:
N=「30.6tmo-C+0.5⎤+td+(th-ζ+tmi/60-λ/15)/24,
(18)
式中,C由下式确定:
(19)
由于太阳在黄道上的运动不是匀速的,而是时快时慢,因此太阳时角并不等于地方时Sd,两者之间的差值称为时差Et,即:
ψ=15(Sd+Et/60-12)。
(20)
地方时与观测时刻、目标经度有关,即:
Sd=th+(tmi-4(15ζ-λ))/60。
(21)
时差与日角有关,即:
Et=0.002 8-1.985 7sinσ+9.905 9sin2σ-
7.092 4cosσ-0.688 2cos2σ。
(22)
根据式(15)~式(22),可以计算出太阳赤纬和太阳时角,将其代入式(14),就可以得到太阳高度角。
在一般情况下,太阳高度角越大,地面目标的太阳光照条件就越好,卫星接收的太阳辐射能量就越多,因而成像质量就越好,但太阳高度角过大,地面反射的太阳辐射能量过多,会影响星下点成像时获取的图像质量。因此,在进行轨道设计时往往将卫星的拍照地方时选择在上午,例如9:30或10:30。
卫星进行侧视成像时,太阳与卫星之间的位置关系随日期、地理位置和地方时变化。当卫星观测方位与太阳入射方位在成像地区形成近似镜面反射条件(卫星高度角与太阳高度角近似相等、卫星方位角与太阳方位角相差180°),并且成像区地表相对平坦时,太阳光的大部分能量被星载遥感器接收,导致获取的图像亮度高于正常水平,甚至过饱和而不可用。
太阳方位角As与太阳高度角Hs有关,即:
(23)
卫星高度角Hz由卫星的侧摆角α决定,两者之间的关系为:
(24)
卫星方位角的计算比较复杂,具体方法请参考相关文献,通过以上公式可以得到太阳高度角、太阳方位角、卫星高度角以及卫星方位角,如果它们之间的关系满足镜面反射条件,则可以考虑删除该观测机会。
5 结束语
通过计算卫星对目标的访问信息,可以得到观测元任务,将这些元任务作为成像卫星任务规划模型的输入数据,采用一定的优化算法进行求解,就可以解决成像卫星任务规划问题。本文提出的敏捷卫星对目标访问信息的计算方法,不仅可以适用于敏捷卫星任务规划,也可以适用于非敏捷卫星任务规划。
[1]李冬,唐容富,易东云.对地观测卫星访问区域目标时间窗口快速算法[J].上海航天,2010,27(3):1-5.
[2]刘晓东.基于MapX的多星协同对对区域目标观测的预处理方法[J].系统工程理论与实践,2010,30(12):2269-2275.
[3]刘晓东.基于空间几何模型的遥感卫星任务分解算法[J].系统工程与电子技术,2011,33(8):1783-1789.
[4]尹璐.多载荷对地观测卫星目标访问计算及任务调度方法的研究 [D].长沙:国防科学技术大学,2012.
[5]黄群东,杨芳,赵键.敏捷卫星宽幅动态成像姿态调整技术研究[J].航天器工程,2013,22(4):17-22.
[6]黄群东,杨芳,赵键.新型敏捷卫星机动中成像模式研究[C]//proceedings of the 第三届高分辨率对地观测学术年会,北京,2014.
[7]霍庆泽.敏捷卫星任意姿态摄影下的姿态计算模型[J].Journal of Aerospace Science and Technology,2015,3(3):54-59.
[8]孙凯,白国庆,陈英武,等.面向动作序列的敏捷卫星任务规划问题[J].国防科技大学学报,2012,34(6):141-148.
[9]郝会成,姜维,李一军,et al.基于Multi-Agent敏捷卫星动态任务规划问题[J].国防科技大学学报,2013,35(1):53-62.
[10]廉振宇,谭跃进,严珍珍.敏捷卫星调度的时间约束推理方法[J].系统工程与电子技术,2013,35(6):1206-1211.
[11]路帅,孙凯,义余江.敏捷卫星任务调度模型、方法及系统研究[C]//第二届高分辨率对地观测学术年会,北京,2013:75-79.
[12]孙凯,邢立宁,陈英武.基于分解优化策略的多敏捷卫星联合对地观测调度[J].计算机集成制造系统,2013,19(1):127-131.
[13]严珍珍,陈英武,邢立宁.基于改进蚁群算法设计的敏捷卫星调度方法[J].系统工程理论与实践,2014,34(3):793-801.
[14]黄群东,杨芳,赵键.敏捷卫星宽幅动态成像姿态调整技术研究[J].航天器工程,2013,22(4):17-22.
[15]谢少波,秦冉冉.敏捷卫星像移补偿残差计算及对成像影响分析[J].航天器工程2013,22(4):12-16.
[16]韩丽,张学庆.基于模拟退火的卫星地面站任务规划方法[J].无线电工程,2010,40(9):42-45.
[17]张超.基于贪婪算法的遥感地面站任务调度技术[J].无线电工程,2011,41(1):58-60.
[18]常飞.卫星地面站数传资源配置优化模型与算法研究[D].长沙:国防科学技术大学,2010.
[19]孔祥海,陈跃庭,李奇,等.一种用于敏捷卫星自主任务规划的云顶高探测方法[J].光学学报,2015,35(7):372-380.
[20]余婧,喜进军,于龙江,等.敏捷卫星同轨多条带拼幅成像模式研究[J].航天器工程,2015,24(2):27-34.
[21]向仍湘.敏捷卫星任务调度技术研究[D].长沙:国防科学技术大学,2010.
[22]杨云刚.敏捷卫星快速机动及稳定方法研究[D].哈尔滨:哈尔滨工业大学,2013.
[23]王淑一,魏春岭,刘其睿.敏捷卫星快速姿态机动方法研究[J].空间控制技术与应用,2011,37(4):36-40.
Calculation Method for Access Information of Agile Satellite on Target
LIU Xiao-dong,WANG Peng,LIN Yuan,GUO Jian-en,HE Chuan-dong,CUI Li,ZOU Dong-dong
(Beijing Remote Sensing Information Institute,Beijing 100192,China)
Task decomposition is a prerequisite for mission planning,and it is essential to calculate the access information of satellite on target,namely,calculate the attitude angle,the actual ground resolution as well as the solar elevation angle.Target coordinates in space geocentric Cartesian coordinate system are first calculated,and the coordinates of the target point in the coordinate system of the satellite orbit are obtained after several coordinate conversions,which can be used to calculate the angle of the two-dimensional pointing angle of satellite on target at the corresponding time.On this basis,according to satellite imaging principle,it is easy to calculate the actual ground resolution of optical satellites or radar satellites.Finally,by calculating the solar declination and the solar hour angle,the solar elevation angle can be obtained.
agile satellite;earth observation;access information;calculate
10.3969/j.issn.1003-3114.2016.05.06
引用格式:刘晓东,王鹏,林元,等.敏捷卫星对目标访问信息的计算方法[J].无线电通信技术,2016,42(5):23-26.
2016-05-16
刘晓东(1981—),男,博士,工程师,主要研究方向:航天任务规划、资源优化配置。郭建恩(1963—),男,博士,研究员,主要研究方向:航天地面系统总体规划与论证。
TP751
A
1003-3114(2016)05-23-4
