基于干扰对齐技术的无线通信系统设计

李　宁，翟立君，刘　允

(中国电子科技集团公司第五十四研究所，河北 石家庄 050081)



基于干扰对齐技术的无线通信系统设计

李宁，翟立君，刘允

(中国电子科技集团公司第五十四研究所，河北 石家庄 050081)

干扰是制约多用户无线通信系统容量的首要因素，传统正交化的干扰管理方式采用分割的方法分配无线资源，每个用户分到的资源随着用户数量的增加而减少，当用户数量较多时会严重降低用户的通信速率。干扰对齐是一种新型的信号处理技术，为提高多用户无线通信系统的容量提供了有效的解决方法。介绍了干扰对齐的基本原理，给出了完整的干扰对齐系统实现方案，包含通信流程、算法设计、信道状态的估计量化及反馈方案。最后，通过仿真验证了干扰对齐的性能。

干扰对齐；MIMO；预编码；信息论

0　引言

在单用户无线通信系统中，信道容量受制于信道带宽和信噪比，其数值由香农定理可以得出。多输入多输出(Multiple Input Multiple Output,MIMO)技术在发送端/接收端配备多根天线，可以使信道容量得到线性提升[1-2]。而在多用户无线通信系统中，由于用户间干扰的存在，单用户信息论不再适用。

当多个无线用户在某个区域共存时，其相互之间的干扰会严重降低用户的信干噪比(Signal to Interference plus Noise Ratio,SINR)，进而影响整个系统的通信性能。目前最主要的解决方法是正交复用，包括时分复用、频分复用和码分复用等。但是正交复用无法解决可用频谱资源受限的问题，随着用户数量的增加，每个用户所能分到的资源非常有限，难以满足高速数据传输的需要。

Maddah-Ali等在研究MIMO X信道自由度时发现，采用一种被称为干扰对齐的方法可以获得比其他任何方式更好的性能[3-4]。Cadambe和Jafar在K用户干扰信道模型基础上建立了干扰对齐的基本理论[5-6]，证明在K用户MIMO干扰信道中，通过一种渐进干扰对齐技术，每个用户都能使其自由度(Degree of Freedom,DoF)达到无干扰情况下的1/2倍，整个系统总的自由度能够达到单个用户无干扰条件下的K/2倍[8]。干扰对齐的研究表明：对多用户无线通信系统，频谱资源并不是有限的，总信道容量并不受用户数量的限制。

本文首先介绍干扰对齐的基本原理，并给出基于干扰对齐技术的3用户2×2MIMO无线通信系统的基本方案以及实现算法，在此基础上对信道状态估计误差、量化误差以及多普勒频移带来的过时误差对系统性能的影响进行了分析，最后通过仿真对干扰对齐的性能进行了验证。

1　干扰对齐理论

干扰对齐的基本原理可由线性方程组来解释。假设一个多用户MIMO系统有K个发射用户和B个接收用户，记xk(1≤k≤K)为用户k的发射信号，yb(1≤k≤B)为第b个用户的接收信号，hij(1≤i≤K,1≤j≤B)为用户j到用户i之间的信道转移矩阵。则从式(1)的线性方程组中可以反映多用户MIMO系统干扰对齐的基本原理。

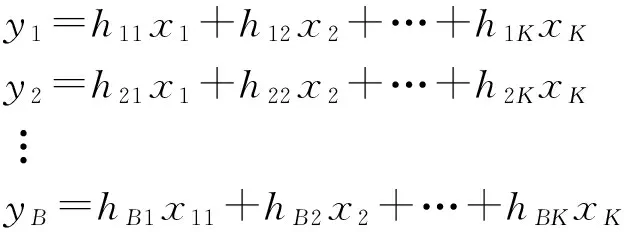
(1)

在上述线性方程组中，未知数的个数为K，方程的个数为B，当K≤B时，方程组有解；当K>B时，无法解出所有未知数，但有可能解出某些未知数。

式(1)可简化表示如下：

Y=H1x1+H2x2+…+HKxK，

(2)

其中，Y=[y1,y2,…,yB]T，Hk=[h1k,h2k,…,hBk]T。

在式(2)中，如果要求接收机能够由观测向量Y解出期望信号x1，则只需要x1的接收波束方向H1不在其他接收波束方向H2,…,HK所张成的矢量空间内，即满足：

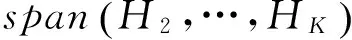
(3)

可以看出，如果能将K-1个干扰波束所张成的空间压缩到更小的子空间中，并使其维度小于B，并使期望信号波束方向与干扰空间正交，则接收机能够在K>B的情况下将期望信号解出。

综上所述，干扰对齐的基本原理是通过某种机制，利用信道分集，在信号空间内将信号进行旋转，将干扰信号对齐到更小的信号子空间中，并使其与期望信号子空间正交，增大期望信号张成的信号子空间，从而提高期望信号空间的自由度和系统容量。

2　3用户干扰对齐通信系统设计

基于上述理论，本文设计了一套干扰对齐技术试验验证系统，目的是对干扰对齐基本理论进行验证，并对干扰对齐算法进行优化。由于当K≥3时才能体现出干扰对齐在自由度方面的优势，而当K>3时，根据文献[10]，K用户干扰信道干扰对齐是NP问题，且其本质没有太大区别，因此本系统选取3用户进行验证。

干扰对齐的信号空间可以在时域、频域和空间域(MIMO)的一个或多个联合域内构建，但由于信号在时间域和频率域内的信道分集难以得到满足，而线性方程组问题在数学上解决方案较为成熟，基于线性预编码(波束赋形)技术，在空间域内实现干扰信号对齐的线性干扰对齐算法是最简单有效的干扰对齐的形式。因此本文系统设计每个用户配备2根天线，系统结构图如图1所示。

图1　干扰对齐试验验证系统示意图

2.1通信流程

干扰对齐的通信流程如图2所示。首先3个发射机以TDMA方式进行信道训练，然后各接收机估计与自己有关的链路的信道信息；主接收机(假设为接收机1)收集其他2个普通接收机所对应的信道状态信息，并通过运行鲁棒性干扰对齐算法来计算每个发射机的预编码矩阵以及对应接收端的均衡矩阵；主接收机将计算所得的预编码矩阵以TDMA的方式分发给各个发射机，再将均衡矩阵分发给其他各个接收机；之后发射机开始发送数据。

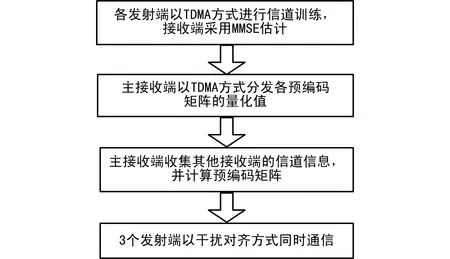
图2　干扰对齐通信流程图

通信的帧格式如图3所示。最初3个时隙分别分配给3个发射机进行轮流的信道训练，在经过一个空闲时隙(用于接收端的计算)后，各接收端也将采用TDMA的方式(第4～6时隙)将计算所得的预编码矩阵反馈给相应的发射端，接下来3个发射端将同时进行传输(同频复用)，直到下一次的信道训练开始。

图3　3用户干扰信道帧格式示意图

2.2干扰对齐算法

对于图1所示的2天线3用户干扰信道，假设每个用户发送1个数据流，3个发射机同时发送，接收机i收到的信号是3个发射机发送信号的叠加，即：

(4)

其中，xk∈2×1，Hkj为从发射机j到接收机k的2×2维MIMO信道转移矩阵，nk∈2×1为接收机k处的加性噪声。

式(4)中，等号右边的第一项是期望信号，第二项是其他用户的干扰，第三项为噪声。可以看到，在多用户系统中，干扰是制约通信质量的主要原因。干扰对齐就是要设计一对预编码向量vk∈2×1和干扰抑制向量uk∈2×1，使得对每个用户都有：

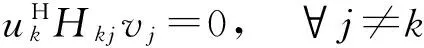
(5)

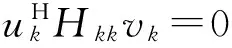
(6)

则干扰信号可以被消除。

vk与uk的求解有很多方法，最方便的方法是直接对线性方程组进行求解[9]。对于3用户2×2 MIMO的情况，对于第一个用户，v1是下面矩阵的任意一个特征向量：

(7)

则可以进一步求得v2和v3，即：

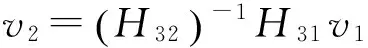
(8)

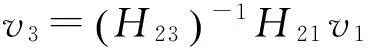
(9)

接收端干扰抑制向量uk的设计只要置于接收信号的正交子空间就可以了，则经过预编码和抑制后的接收信号可以表示为：

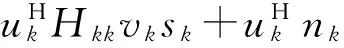
(10)

式中，sk为发送数据符号。可以看出，经过干扰对齐的预编码之后，干扰信号被完全消除。

2.3信道估计与反馈

从式(7-9)可以看出，干扰对齐的算法的实现依赖于信道状态信息(Channel State Information ，CSI)。本系统采用发送训练序列进行信道估计的方式获得CSI。

训练序列矩阵采用酉矩阵(可以证明，在MIMO信道中采用酉阵作为训练矩阵是均方误差(Mean Square Error,MSE)最优的)。接收机采用MMSE估计信道矩阵H：

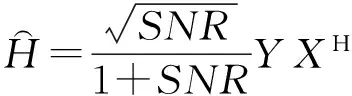
(11)

在信道估计后，接收端需要将CSI反馈给发射端。传统的反馈策略是将所有信道矩阵反馈给每一个发射端，因此会带来较大的信令开销，因而本系统提出基于预编码矩阵的反馈策略，即接收端根据信道估计结果计算出vk，并将计算结果反馈给发射端。为了进一步降低反馈开销，先生成码本，在对vk进行量化后，仅反馈码本上对应的编码。根据Rate-Distortion理论，当量化比特数Nf=d(M-d)·logSNR时，量化误差所带来的干扰泄漏将控制在O(1)的水平，即不会对自由度造成任何影响。

3　信道误差分析

在干扰对齐的实现过程中，误差来源主要包括信道的估计误差、量化误差以及过时误差。从2.3节中可以看出，对于CSI的估计误差以及量化误差，都可以控制在不影响自由度的范围内[11]。对于信道的过时误差，其大小取决于信道的变化快慢速度(即多普勒频移)，无法保证系统的自由度不受影响。但可以预见，当信道变化很慢时，系统速率的下降将非常小，而当信道变化较快时，干扰对齐和TDMA都将进入速率平层，即自由度一起降为0，但干扰对齐较TDMA还是会有速率增益，这一点将在第4部分的仿真中进行验证。

4　仿真验证

本文对图1中的两天线3用户干扰信道下的干扰对齐算法进行了仿真。仿真基于MATLAB R2012b软件。仿真中，假设信道为加性白高斯噪声信道，且信道噪声功率归一化为1，每个用户采用同样的发送功率。仿真结果与传统的TDMA传输模式进行了对比。仿真也对CSI估计误差、量化误差以及过时误差带来的影响进行了评估。

图4给出了干扰对齐传输与TDMA传输分别在理想CSI与估计CSI情况下的传输容量比较结果。从图中可以看出，在两种情形下(理想CSI与估计CSI)，采用干扰对齐技术均能实现1.5倍于TDMA的传输速率，这与自由度结果(干扰对齐所能实现的自由度为3，TDMA传输的自由度为2)所给出的容量预测是一致的。

另外也能看出，由于估计CSI带来的误差会导致一定的速率损失，但没有影响自由度。这是因为，采用MMSE估计所对应的估计均方误差为1/(1+SNR)，即量级为SNR-1，这意味着因为信道估计误差所带来的自干扰功率量级为O(1)Θ(1)，与噪声功率相当，因而并不会造成系统自由度的损失。

图4　干扰对齐与TDMA传输容量比较(理想CSI与估计CSI)

图5给出了同时存在CSI估计误差与量化误差(量化对象为预编码矩阵)时干扰对齐与TDMA传输的性能比较。从图中可以看出，在考虑了CSI量化误差后，干扰对齐的自由度较没有CSI量化误差的情形并没有降低，但会带来约2 bps的速率降低。

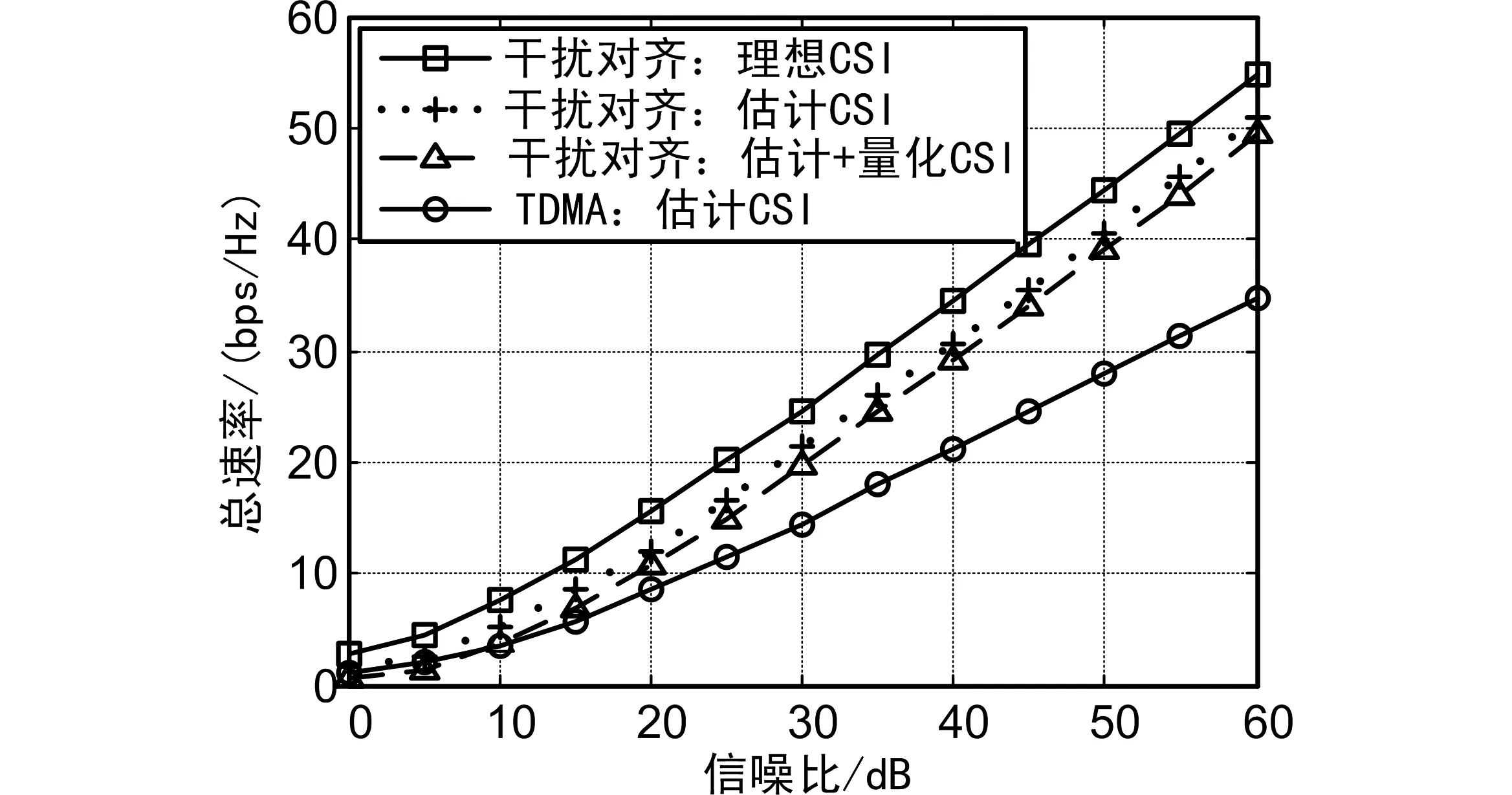
图5　信道估计误差及量化误差对干扰对齐的影响

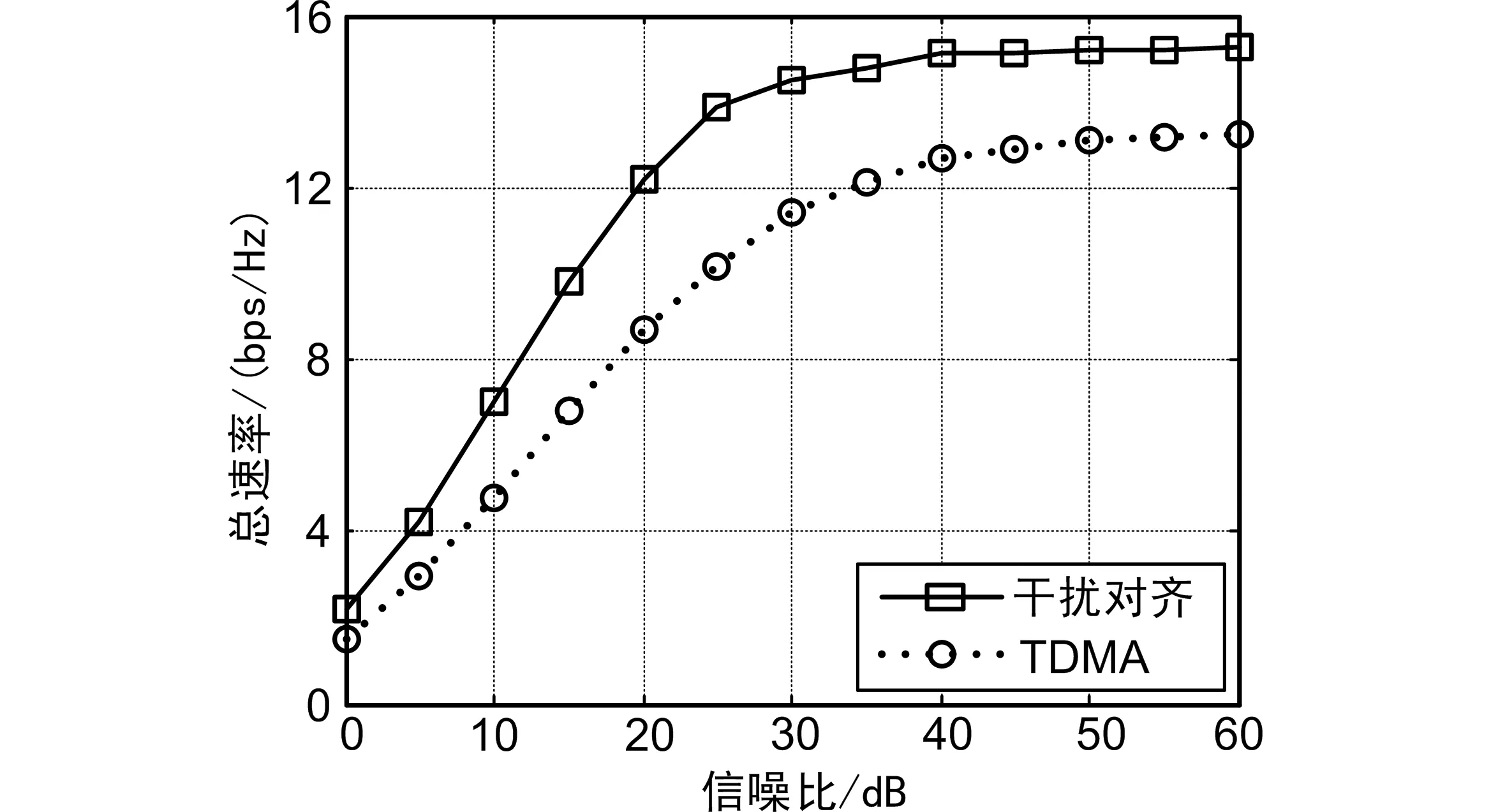
图6　信道过时误差对干扰对齐的影响

4　结束语

干扰对齐理论从根本上改变了人们对多用户系统干扰管理的方式，介绍了干扰对齐的基本原理，并给出了基于干扰对齐技术的3用户2×2MIMO无线通信系统设计方案，采用经典干扰对齐算法，对系统性能进行了仿真。仿真结果充分证明干扰对齐相比传统的正交传输方法在系统容量方面具有显著优势，即使在存在估计误差、量化误差和过时误差的情况下，这一优势仍然非常明显。因此，干扰对齐技术在提高无线通信系统的传输容量方面，有着广阔的应用前景。

[1]Goldsmith A.Wireless Communications[M].Cambridge：Cambridge University Press,2004：321-350.

[2]Tse D,Viswanath P.Fundamentals of Wireless Communication[M].Cambridge：Cambridge University Press,2005：290-331.

[3]Maddah-Ali M,Motahari A，Khandani A.Communication over X Channel:Signaling and Multiplexing Gain[R].in Technical Report.UW-ECE-2006-12,University of Waterloo,July 2006：1-19.

[4]Maddah-Ali M A,Motahari A S,Khandani A K.Communication over MIMO X Channels:Interference Alignment,Decomposition,and Performance Analysis[J].IEEE Transactions on Information Theory,2008,54(8)：3457-3470.

[5]Gou T,Jafar S.Degrees of Freedom of the K User M×N MIMO Interference Channel[J].IEEE Transactions on Information Theory,2010,56(12)：6040-6057.

[6]Sun Hua,Gou Tiangao,Jafar S A.Degrees of Freedom of MIMO X Networks:Spatial Scale Invariance and One-Sided Decomposability[J].IEEE Transactions on Information Theory,2013,59(12)：8377-8385.

[7]Gomadam K,Cadambe V R,Jafar S A.A Distributed Numerical Approach to Interference Alignment and Applications to Wireless Interference Networks[J].IEEE Transactions on Information Theory,2011,57(6)：3309-3322.

[8]Cadambe V R,Jafar S A.Interference Alignment and Degrees of Freedom of the K-user Interference Channel[J].IEEE Transactions on Information Theory,2008,54(8):3425-3441.

[9]Gonzalez O,Ramirez D,Santamaria I.Experimental Validation of Interference Alignment Techniques using a Multiuser MIMO Testbed[C]//IEEE International ITG Workshop on Smart Antennas (WSA),2011:1-8.

[10]Razaviyayn M,Sanjabi M,Luo Z Q.Linear Transceiver Design for Interference Alignment:Complexity and Computation[J].IEEE Transactions on Information Theory,2012,58(5) :2896 -2910.

[11]钱进,孙银江,郭 磊,等.基于干扰对齐的能量效率优化算法分析[J].移动通信,2016,40(2):66-73.

Design of Wireless Communication System Based on Interference Alignment

LI Ning,ZHAI Li-jun,LIU Yun

(The 54th Research Institute of CETC,Shijiazhuang Hebei 050081,China)

Interference is the main restriction to the capacityof multi-user wireless communication system.The traditional method for interference management is orthogonalization,which split the radio resource for users.The larger the user number,the resource assigned to each user is less,leading to data rate per user declined significantly.Interference alignment (IA) is a novel signal processing technique which provides a useful method for improving the capacity of multi-user wireless communication system.In this paper,the basic theory of IA is introduced.Then,the whole implementation scheme of IA is provided,including communication procedures,algorithm design,quantized channel state estimate and feedback method.Finally,the performance of IA is validated by simulation

Interference alignment; MIMO; Pre-coding; Information theory

10.3969/j.issn.1003-3114.2016.05.03

引用格式：李宁，翟立君，刘允.基于干扰对齐技术的无线通信系统设计[J].无线电通信技术,2016,42(5):10-13,41.

2016-05-19

中国电子科技集团公司第五十四研究所发展基金(X1228156)

李宁(1981—)，女，高级工程师，主要研究方向：无线通信与干扰管理。翟立君(1981—)，男，高级工程师/博士，主要研究方向：卫星移动通信。

TN 919.3

A

1003-3114(2016)05-10-4